Engage NY Eureka Math 4th Grade Module 4 Mid Module Assessment Answer Key
Eureka Math Grade 4 Module 4 Mid Module Assessment Answer Key
Question 1.
Follow the directions below to draw a figure in the box below. Use a straightedge.
a. Draw 2 points, A and B.
b. Draw 
.
c. Draw point D that is not on .
d. Draw \(\overrightarrow{B D}\).
e. Draw \(\overline{A D}\).
f. Name an acute angle.
__________________________
g. Name an obtuse angle. You may have to draw and label another point.
____________________
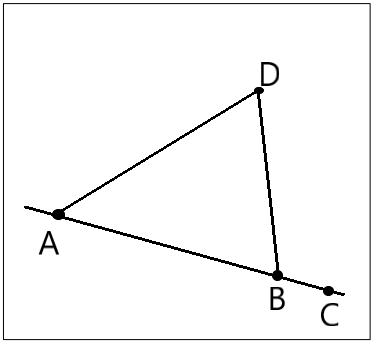
Answer:
The acute angle is <BAD.
Here we labeled C as another point. So the obtuse angle is <DBC
Explanation:
Here, we have to draw two points and then labeled them as A and B.
And use a straight line to draw AB.
Now we have to draw a new point that is not on AB and we label it as D.
Then we will Join BD with a line to get an acute angle BAD.
Use a straight line to join AD.
And for an obtuse angle, we need to label another point as C.
We will use these points and we will label with one angle as <BAD/<DBC
Question 2.
Use your protractor to measure the angle indicated by the arc. Classify each angle as right, acute, or obtuse. Explain how you know each angle’s classification.
a.
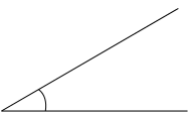
Answer:
The angle indicated by the arc is 30° which is an acute angle.
Explanation:
Here the angle we measured is an acute angle because it indicates 30° which is less than the right angle i.e 90°Â
b.
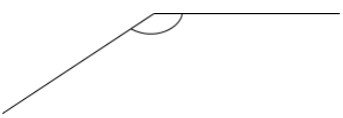
Answer:
The answer is 147° which is an obtuse angle.
Explanation:
Here it is an obtuse angle as it measures 147° which is greater than a right angle and less than 180°
c.
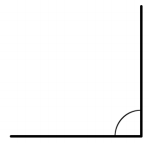
Answer:
The angle indicated by the arc is 90° which is a right-angled triangle.
Explanation:
This is a right-angled triangle as it exactly measures 90°.
Question 3.
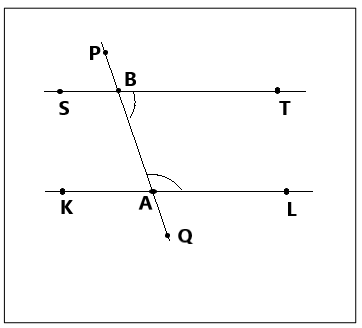
Use the following instructions to draw a figure in the box below.
- Using a straightedge, draw a line. Label it
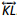. - Label a point A on .
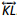- Using your protractor and ruler, draw a line perpendicular to 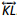through point A.
- Label the perpendicular line
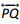. - Label a point B on 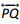, other than point A.
- Using your protractor and straightedge, draw a line,
, perpendicular to through point B. - Which lines are parallel in your drawing? Explain why.
Answer:
ST||KL
Here ST is parallel to KL because both of them are perpendicular to PQ. It shows us the sides of a rectangle.
Explanation:
By using a straight edge draw a line and label them as KL.
Now label a point on the line of KL and name the point as A.
Next, draw a perpendicular line by using the protractor and ruler through point A to KL.
And label the perpendicular line as PQ.
Name point B on PQ other than point A.
Next is to draw a line ST by using the protractor and straightedge perpendicular to PQ through point B.
Now the answer to the above-mentioned questioned in our drawing is ST is parallel to KL as both of them are perpendicular to PQ.
Question 4.
Use the clock to answer the following:
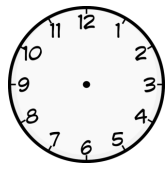
a. Use a straightedge to draw the hands as they would appear at 3:00.
Answer:
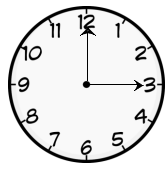
Explanation:
Given in the above diagram draw a line at minutes hand which is 3:00
b. What kind of angle is formed by the clock hands at 3:00?
Answer:
A right angle.
Explanation:
By observing keenly in the above diagram we get a right angle formed by the clock hands at 3:00
c. What time will it be when the minute hand has turned 180°?
Answer:
It will be at 3.30.
Explanation:
By turning the minute hand to 180° the time we get is 3.30
d. How many 90° turns will the minute hand make between 3:00 and 4:00?
Answer:
The minute’s hand will make four 90 turns between 3:00 and 4:00
Explanation:
By observing in the diagram when the clock is rotating in a clockwise direction the minute hand make four 90° turns i.e at 3:00, 3:15, 3:30, 3:45, 4:00
Question 5.
Use the compass rose to answer the following:
a. Maddy faced East. She turned to her right until she was facing North. How many degrees did she turn?
Answer:
Maddy turned 270°.
Explanation:
Maddy is facing the east side as she turned to her right means she is moving towards the south which is 90. As mentioned in the question Maddy turns right until she reaches north
So to reach north she as to make a move of 90°. Now from East to North she has made 270° i.e ( 90°+90°+90°).
b. Quanisha was facing North. She turned toward her right until she faced East. Alisha was facing South. She turned toward her right until she faced West. What fraction of a full turn did each girl complete? Through how many degrees did each girl turn?
Answer:
Here each girl completed 1/4th of a full turn.
And each girl turned 90°.
Explanation:
As Quanisha was facing north she turned towards the right until she reaches her destination which is East that she needs to face. Another girl Alisha was facing south and turned toward her right until she faces west. So by observing the direction through the compass given above here each girl completed their turn is 1/4th. And also each girl turned 90° while moving to their destination.
Question 6.
The town of Seaford has a large rectangular park with a biking path around its perimeter and two straight-line biking paths that cut across it as shown in the diagram below.
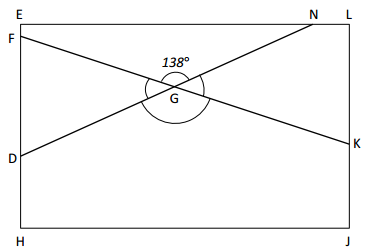
a. Find the measure of the following angles using a protractor.
∠FGD:
∠GDK:
∠KGN:
Answer:
By using a protractor, here the measuring angle of ∠FGD is 42° ( 180° -138° = 42°)
By doing the same above process the measuring angle of ∠GDK is 138°
The measuring angle of ∠KGN is 42° ( 180° -138° = 42°)
Explanation:
To measure an angle FGD, we place the midpoint of the protractor on the vertex G of the angle. The marking on the inner circle of the protractor is 0° to 180°. Now take the difference of the protractor as 180 and 138° we will get 42°. Repeat the same process to measure the other angles.
b. In the space below, use a protractor to draw an angle with the same measure as ∠DGK.
Answer:
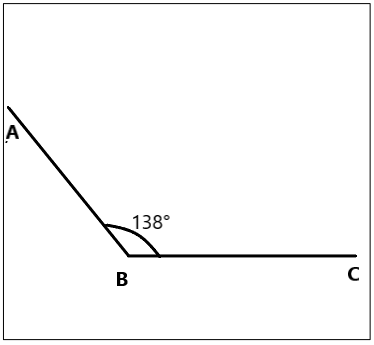
Explanation:
Here the same measure as ∠DGK is 138°. Now, take the protractor to draw an angle 138° and mention the angle as ∠ABC.
c. Below is a sign that bikers may encounter while riding in the park. Using the points in the figure below, identify a line segment, a right angle, an obtuse angle, a set of parallel lines, and a set of perpendicular lines. Write them in the table below.
Answer:
Line segment: EF
Right Angle: ∠ABD
Obtuse angle: ∠GHJ
Parallel Lines: KL||GH
Perpendicular lines: AC ⊥ BD
Explanation:
Line Segment: A-line that is bounded by two endpoints are in the above diagram are EF.
Right Angle: A right angle is an angle of exactly 90°. So by observing the above diagram we can identify the ∠ABD is a right angle.
Parallel Lines: The two straight lines in a plane that do not meet at any point are called to be parallel lines. By observing the diagram we got to know that KL is parallel to the GH.
Perpendicular Lines: Any two distinct lines meeting each other at 90° or a right angle are perpendicular lines. By keenly observing the diagram AC is perpendicular to BD.