Engage NY Eureka Math 4th Grade Module 3 Lesson 9 Answer Key
Eureka Math Grade 4 Module 3 Lesson 9 Problem Set Answer Key
Question 1.
Solve using each method.
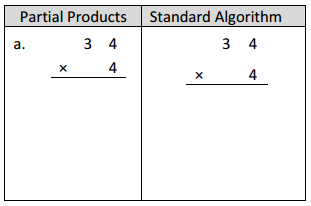
Answer:
Explanation:
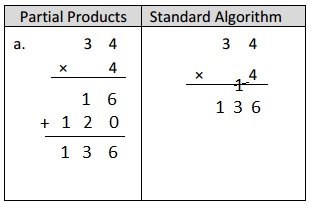
Given expression as 4 X 34 =
Partial Products
34
X 4
16
+120
136 ,
Here we first write multiplication of 4 X 4 ones, then
4 X 3 tens then add as shown above 16 + 120 = 136,
In standard algorithm we add same time of multiplying as
1
34
X 4
136 ,here 4 X 4 ones= 16 ones we write 6 at ones place and take 1 at tens place then 4 x 3 at tens place = 12 tens
add 1 ten to 12 tens we get 13 tens so 4 X 34 = 136.
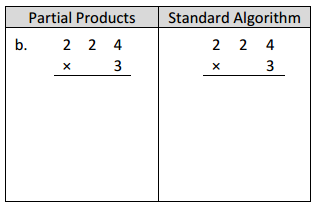
Answer:
Explanation:
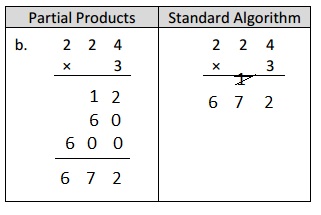
Given expression as 3 X 224 =
Partial Products
224
X 3
12
60
+600
672 , Here we first write multiplication of 3 X 4 ones, then
3 X 2 tens and 3 X 2 hundreds then add as shown above
12 + 60 + 600 = 672,
In standard algorithm we add same time of multiplying as
1
224
X 3
672 ,here 3 X 4 ones = 12 ones we write 2 at ones place and
take 1 at tens place then 3 x 2 tens = 6 tens add 1 ten to 6 tens
we get 7 tens and 3 X 2 hundreds = 6 hundreds, so 4 X 244 = 672.
Question 2.
Solve. Use the standard algorithm.
a.
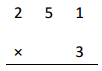
Answer:
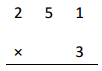
7 5 3
Explanation:
In standard algorithm we add same time of multiplying as
1
251
X 3
753 ,here 3 X 1 ones = 3 ones then 3 x 5 tens = 15 tens
we write 5 at tens place and take 1 to hundred place and
3 X 2 hundreds = 6 hundreds, now adding 1 hundred to
6 hundreds we get 7 hundreds , so 3 X 251 = 753.
b.
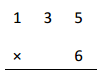
Answer:
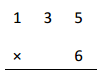
8 1 0
Explanation:
In standard algorithm we add same time of multiplying as
1, 3
135
X 6
810 ,here 6 X 5 ones = 30 ones, we write 0 at ones place and
take 3 to tens places then 6 x 3 tens = 18 tens + 3 tens = 21 tens,
we write 1 at tens place and take 2 to hundred place and
6 X 1 hundred = 6 hundreds, now adding 2 hundreds to
6 hundreds we get 8 hundreds , so 6 X 135 = 810.
c.
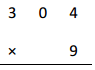
Answer:

2, 7 3 6
Explanation:
In standard algorithm we add same time of multiplying as
3
304
X 9
2,736 ,here 9 X 4 ones = 36 ones, we write 6 at ones place and
take 3 to tens places then 9 x 0 ten = 0 ten + 3 tens = 3 tens,
9 X 3 hundreds = 27 hundreds, now we write 7 at hundreds place
and 2 at thousands place as shown above, So 9 X 304 = 2,736.
d.
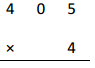
Answer:
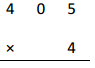
1, 6 2 0
Explanation:
In standard algorithm we add same time of multiplying as
2
405
X 4
1,620 ,here 4 X 5 ones = 20 ones, we write 0 at ones place and
take 2 to tens places then 4 x 0 ten = 0 ten + 2 tens = 2 tens,
4 X 4 hundreds = 16 hundreds, now we write 6 at hundreds place
and 1 at thousand place as shown above, So 4 X 405 = 1,620.
e.
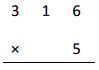
Answer:
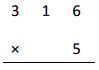
1, 5 8 0
Explanation:
In standard algorithm we add same time of multiplying as
3
316
X 5
1,580 ,here 5 X 6 ones = 30 ones, we write 0 at ones place and
take 3 to tens places then 5 x 1 ten = 5 tens + 3 tens = 8 tens,
5 X 3 hundreds = 15 hundreds, now we write 5 at hundreds place
and 1 at thousand place as shown above, So 5 X 316 = 1,580.
f.
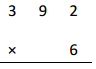
Answer:
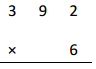
2, 3 5 2
Explanation:
In standard algorithm we add same time of multiplying as
5,1
392
X 6
2,352 ,here 6 X 2 ones = 12 ones, we write 2 at ones place and
take 1 to tens places then 6 x 9 tens = 54 tens + 1 tens = 55 tens,
we write 5 at tens place and take another 5 to hundreds place,
6 X 3 hundreds = 18 hundreds,18 hundreds + 5 hundreds =
23 hundreds now we write 3 at hundreds place
and 2 at thousands place as shown above, So 6 X 392 = 2,352.
Question 3.
The product of 7 and 86 is ________.
Answer:
The product of 7 and 86 is 602,
Explanation:
Give to find the product of 7 and 86 is
4
86
X 7
602
first we multiply 7 with 6 ones = 42 ones we write 2 at ones
place and take 4 to tens place now 7 X 8 = 56 tens adding
4 tens we get 60 tens, So 7 X 86 = 602.
Question 4.
9 times as many as 457 is _________.
Answer:
9 times as many as 457 is 4,113,
Explanation:
Given to find 9 times as many as 457 is
6
457
X 9
4,113 ,here 9 X 7 ones = 63 ones, we write 3 at ones place and
take 6 to tens places then 9 x 5 tens = 45 tens + 6 tens = 51 tens,
we write 1 at tens place and take 5 to hundreds place,
9 X 4 hundreds = 36 hundreds, 36 hundreds + 5 hundreds =
41 hundreds now we write 1 at hundred place
and 4 at thousands place as shown above, So 9 X 457 = 4,113.
Question 5.
Jashawn wants to make 5 airplane propellers. He needs 18 centimeters of wood for each propeller. How many centimeters of wood will he use?
Answer:
Jashawn needs 90 centimeters of wood to make
5 airplane propellers,
Explanation:
Given Jashawn wants to make 5 airplane propellers.
He needs 18 centimeters of wood for each propeller.
So number of centimeters of wood will he use is 5 X 18 cms =
4
18
X 5
90
here first we multiply 5 X 8 ones = 40 ones, we write 0
at ones place and take 4 to tens place then 5 X 1 ten =
5 tens+ 4 tens = 9 tens, So 5 X 18 = 90 centimeters,
therefore, Jashawn needs 90 centimeters of wood to make
5 airplane propellers.
Question 6.
One game system costs $238. How much will 4 game systems cost?
Answer:
4 game systems will cost $952,
Explanation:
Given one game system costs $238. So for 4 game
systems it will cost 4 X $238 =
1, 3
$238
X 4
952
here first we multiply 4 X 8 ones = 32 ones,
we write 2 at ones place and take 3 to tens places
then 4 x 3 tens = 12 tens + 3 tens = 15 tens,
we write 5 at tens place and take 1 to hundred place,
4 X 2 hundreds = 8 hundreds, now 8 hundreds + 1 hundred =
9 hundreds, So 5 X $238 = 952, therefore 4 game systems will cost $952.
Question 7.
A small bag of chips weighs 48 grams. A large bag of chips weighs three times as much as the small bag. How much will 7 large bags of chips weigh?

Answer:
7 large bags of chips weigh 1,008 grams,
Explanation:
Given a small bag of chips weighs 48 grams.
A large bag of chips weighs three times as much as
the small bag means 3 X 48 grams=
2
48
X 3
144
here first we multiply 3 X 8 ones = 24 ones, we write 4
at ones place and take 2 to tens place then 3 X 4 ten =
12 tens+ 2 tens = 14 tens, we write 14 tens as 4 at tens place
and 1 at hundreds place, So 3 X 48 grams = 144 grams,
Now 7 large bags of chips weigh 7 X 144 grams =
3,2
144
X 7
1,008
here first we multiply 7 X 4 ones = 28 ones, we write 8
at ones place and take 2 to tens place then 7 X 4 ten =
28 tens+ 2 tens = 30 tens, we write 30 tens as 0 at tens place
and other 3 at hundreds place,now 7 X 1 hundred = 7 hundred,
7 hundred + 3 hundreds = 10 hundreds we write 0 at
hundreds place at 1 at thousands place, So 7 X 144 = 1,008 grams,
therefore, 7 large bags of chips weigh 1,008 grams.
Eureka Math Grade 4 Module 3 Lesson 9 Exit Ticket Answer Key
Question 1.
Solve using the standard algorithm.
a.
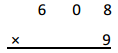
Answer:
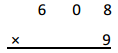
5, 4 7 2
Explanation:
In standard algorithm we add same time of multiplying as
7
608
X 9
5,472 ,here 9 X 8 ones = 72 ones, we write 2 at ones place and
take 7 to tens places then 9 x 0 tens = 0 tens + 7 tens = 7 tens,
we write 7 at tens place and 9 X 6 hundreds = 54 hundreds,
now we write 4 at hundreds place and 5 at thousands place as shown above, So 9 X 608 = 5,472.
b.
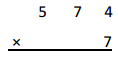
Answer:
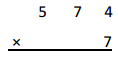
4, 0 1 8
Explanation:
In standard algorithm we add same time of multiplying as
2
574
X 7
4,018 ,here 7 X 4 ones = 28 ones, we write 8 at ones place and
take 2 to tens places then 7 x 7 tens = 49 tens + 2 tens = 51 tens,
we write 1 at tens place and 5 at hundreds place and
7 X 5 hundreds = 35 hundreds, 35 hundreds + 5 hundreds =
40 hundreds,now we write 0 at hundreds place and 4
at thousands place as shown above, So 7 X 574 = 4,018.
Question 2.
Morgan is 23 years old. Her grandfather is 4 times as old. How old is her grandfather?
Answer:
Morgan’s grandfather is 92 years old,
Explanation:
Given Morgan is 23 years old and her grandfather is 4 times
as old. So Morgan’s grandfather’s is 4 X 23 years =
1
23
X 4
92, here 4 X 3 ones = 12 ones, we write 2 at ones place and
take 1 to tens places then 4 x 2 tens = 8 tens, 8 tens + 1 ten =
9 tens, So Morgan’s grandfather is 92 years old.
Eureka Math Grade 4 Module 3 Lesson 9 Homework Answer Key
Question 1.
Solve using each method.
Answer:
Explanation:
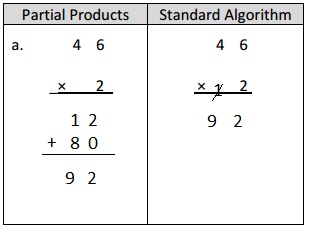
Given expression as 2 X 46 =
Partial Products
46
X 2
12
+80
92 , Here we first write multiplication of 2 X 6 ones, then
2 X 4 tens then add as shown above 12 + 80 = 92,
In standard algorithm we add same time of multiplying as
1
46
X 2
92 ,here 2 X 6 ones= 12 ones we write 2 at ones place and take 1
at tens place then 2 x 4 at tens place = 8 tens
add 1 ten to 8 tens we get 9 tens so 2 X 46 = 92.
Answer:
Explanation:
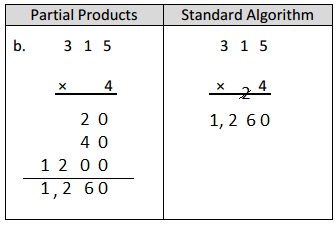
Given expression as 4 X 315 =
Partial Products
315
X 4
20
40
+1200
1,260 , Here we first write multiplication of 4 X 5 ones, then
4 X 1 ten and 4 X 3 hundreds then add as shown above
20 + 40 + 1,200 = 1,260,
In standard algorithm we add same time of multiplying as
2
315
X 4
1,260 ,here 4 X 5 ones = 20 ones we write 0 at ones place and
take 2 at tens place then 4 x 1 tens = 4 tens add 2 tens to 4 tens
we get 6 tens and 4 X 3 hundreds = 12 hundreds, we write 2 at
hundreds and 1 at thousands places, so 4 X 315 = 1,260.
Question 2.
Solve using the standard algorithm.
a.
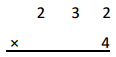
Answer:
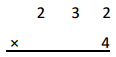
9 2 8
Explanation:
In standard algorithm we add same time of multiplying as
1
232
X 4
928 ,here 4 X 2 ones = 8 ones then 4 x 3 tens = 12 tens
we write 2 at tens place and take 1 to hundred place and
4 X 2 hundreds = 8 hundreds, now adding 1 hundred to
8 hundreds we get 9 hundreds , so 4 X 232 = 928.
b.
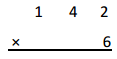
Answer:
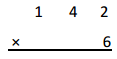
8 5 2
Explanation:
In standard algorithm we add same time of multiplying as
2, 1
142
X 6
852 ,here 6 X 2 ones = 12 ones, we write 2 at ones place and
take 1 to tens places then 6 x 4 tens = 24 tens + 1 tens = 25 tens,
we write 5 at tens place and take 2 to hundred place and
6 X 1 hundred = 6 hundreds, now adding 2 hundreds to
6 hundreds we get 8 hundreds , so 6 X 142 = 852.
c.
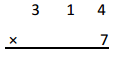
Answer:
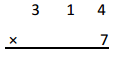
2, 1 9 8
Explanation:
In standard algorithm we add same time of multiplying as
2
314
X 7
2,198 ,here 7 X 4 ones = 28 ones, we write 8 at ones place and
take 2 to tens places then 7 x 1 ten = 7 tens + 2 tens = 9 tens,
7 X 3 hundreds = 21 hundreds, now we write 1 at hundreds place
and 2 at thousands place as shown above, So 7 X 314 = 2,198.
d.
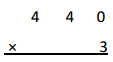
Answer:

1, 3 2 0
Explanation:
In standard algorithm we add same time of multiplying as
1
440
X 3
1,320 ,here 3 X 0 ones = 0 ones, we write 0 at ones place,
3 x 4 tens = 12 tens we write 2 at tens place and take 1
at hundreds place, 3 X 4 hundreds = 12 hundreds,
12 hundreds + 1 hundred = 13 hundreds ,now we write 3
at hundreds place and 1 at thousand place as shown above,
So 3 X 440 = 1,320.
e.
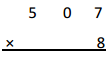
Answer:
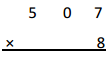
4, 0 5 6
Explanation:
In standard algorithm we add same time of multiplying as
5
507
X 8
4,056 ,here 8 X 7 ones = 56 ones, we write 6 at ones place and
take 5 to tens places then 8 x 0 tens = 0 tens + 5 tens = 5 tens,
we write 5 at tens place, 8 X 5 hundreds = 40 hundreds,now we write
0 at hundreds place and 4 at thousands place as shown above,
So 8 X 507 = 4,056.
f.
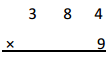
Answer:

3, 4 5 6
Explanation:
In standard algorithm we add same time of multiplying as
7, 3
384
X 9
3,456 ,here 9 X 4 ones = 36 ones, we write 6 at ones place and
take 3 to tens places then 9 x 8 tens = 72 tens + 3 tens = 75 tens,
we write 5 at tens places 7 at hundreds place and
9 X 3 hundreds = 27 hundreds, 27 hundreds + 7 hundreds =
34 hundreds now we write 4 at hundreds place and
3 at thousands place as shown above,
So 9 X 384 = 3,456.
Question 3.
What is the product of 8 and 54?
Answer:
The product of 8 and 54 is 432,
Explanation:
Give to find the product of 8 and 54 is
3
54
X 8
432
first we multiply 8 with 4 ones = 32 ones we write 2 at ones
place and take 3 to tens place now 8 X 5 = 40 tens adding
3 tens we get 43 tens, So 8 X 54 = 432.
Question 4.
Isabel earned 350 points while she was playing Blasting Robot. Isabel’s mom earned 3 times as many points as Isabel. How many points did Isabel’s mom earn?
Answer:
Isabel’s mom earn 1050 points,
Explanation:
Given Isabel earned 350 points while she was playing Blasting Robot. Isabel’s mom earned 3 times as many points as Isabel. So points did Isabel’s mom earn is 3 X 350 =
1
350
X 3
1050,
first we multiply 3 with 0 ones = 0 ones ,
3 X 5 = 15 tens we write 15 tens as 5 at tens place and
1 at hundreds place and 3 X 3 = 9 hundreds + 1 hundred =
10 hundreds we write 10 hundreds as 0 at hundreds place and
1 at thousands place, So 3 X 350 = 1050.
Therefore, Isabel’s mom earn 1050 points.
Question 5.
To get enough money to go on a field trip, every student in a club has to raise $53 by selling chocolate bars. There are 9 students in the club. How much money does the club need to raise to go on the field trip?
Answer:
The club needs to raise $477 to go on the field trip,
Explanation:
Given to get enough money to go on a field trip, every student in a club has to raise $53 by selling chocolate bars.
There are 9 students in the club. So money does the club need to raise to go on the field trip is 9 X $53 =
2
$53
X 9
$477
first we multiply 9 with 3 ones = 27 ones , we write 7 at
ones place and 2 at tens place, 9 X 5 tens= 45 tens,
45 tens + 2 tens = 47 tens we write 47 tens as
7 at tens place and 4 at hundreds place so 9 X $53 = $477,
therefore,the club needs to raise $477 to go on the field trip.
Question 6.
Mr. Meyers wants to order 4 tablets for his classroom. Each tablet costs $329. How much will all four tablets cost?
Answer:
Total cost for all four tablets are $1,316,
Explanation:
Given Mr. Meyers wants to order 4 tablets for his classroom.
Each tablet costs $329. So total cost for four tablets are
4 X $329 =
1,3
$329
X 4
$ 1,316
first we multiply 4 with 9 ones = 36 ones , we write 6 at
ones place and 3 at tens place, 4 X 2 tens= 8 tens,
8 tens + 3 tens = 11 tens we write 11 tens as
1 at tens place and 1 at hundreds place, Now 4 X 3 hundreds =
12 hundreds, 12 hundreds + 1 hundred = 13 hundreds, we write
3 at hundreds place and 1 at thousands place, So 4 X $329 = $1,316.
Question 7.
Amaya read 64 pages last week. Amaya’s older brother, Rogelio, read twice as many pages in the same amount of time. Their big sister, Elianna, is in high school and read 4 times as many pages as Rogelio did. How many pages did Elianna read last week?
Answer:
Elianna read 512 pages last week,
Explanation:
Given Amaya read 64 pages last week. Amaya’s older brother, Rogelio, read twice as many pages in the same amount of time.
So Rogelio reads 2 X 64 pages =
64
X 2
128
2 X 4 ones = 8 and 2 X 6 tens= 120, So 2 X 64 = 8 + 120 = 128,
So Rogelio reads 128 pages,
Their big sister, Elianna, is in high school and read 4 times as
many pages as Rogelio did. So number of pages did
Elianna read last week are 4 X 128 pages=
1, 3
128
x 4
512
here we first we multiply 4 with 8 ones = 32 ones ,
we write 2 at ones place and 3 at tens place, 4 X 2 tens= 8 tens,
8 tens + 3 tens = 11 tens we write 11 tens as
1 at tens place and 1 at hundreds place and 4 X 1 hundred =
4 hundreds, 4 hundreds +1 hundred = 5 hundreds,
So
4 X 128 pages = 512 pages,
therefore, Elianna read 512 pages last week.