Engage NY Eureka Math 4th Grade Module 3 Lesson 8 Answer Key
Eureka Math Grade 4 Module 3 Lesson 8 Problem Set Answer Key
Question 1.
Represent the following expressions with disks, regrouping as necessary, writing a matching expression, and recording the partial products vertically as shown below.
a. 1 × 213
1 × _2__ hundreds + 1 × _1__ ten + 1 × _3__ ones
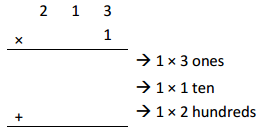
Answer:

Explanation:
Represented the following expression 1 X 213 with disks,
regrouped as necessary. Wrote a matching expression 1 X 213 = 213
and recorded the partial products vertically as shown above.
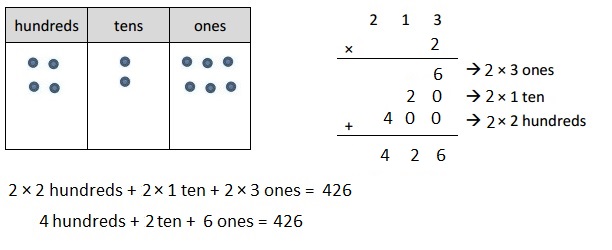
b. 2 × 213

Answer:
Explanation:
Represented the following expression 2 X 213 with disks,
regrouped as necessary. Wrote a matching expression 2 X 213 = 426
and recorded the partial products vertically as shown above.
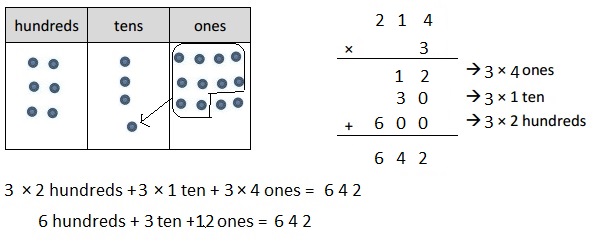
c. 3 × 214

Answer:
Explanation:
Represented the following expression 3 X 214 with disks,
regrouped as necessary. Wrote a matching expression 3 X 214 = 642
and recorded the partial products vertically as shown above.
d. 3 × 1,254
Answer:
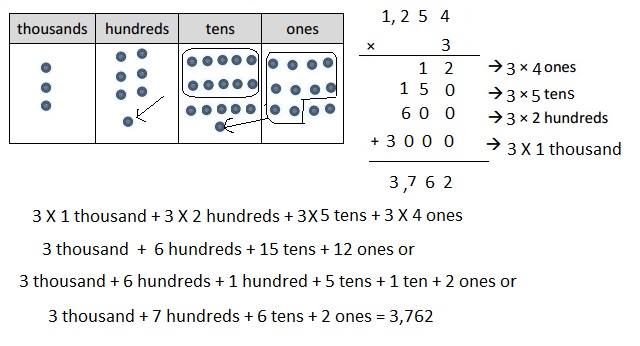
Explanation:
Represented the following expression 3 X 1,254 with disks,
regrouped as necessary. Wrote a matching expression 3 X 1,254 = 3,762
and recorded the partial products vertically as shown above.
Question 2.
Represent the following expressions with disks, using either method shown during class, regrouping as necessary. To the right, record the partial products vertically.
a. 3 × 212
Answer:
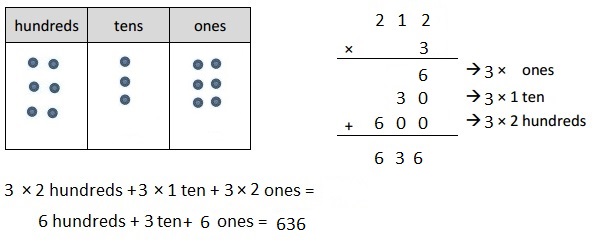
Explanation:
Represented the following expression 3 X 212 with disks, regrouped as necessary and recorded the partial products vertically as shown above.
b. 2 × 4,036
Answer:
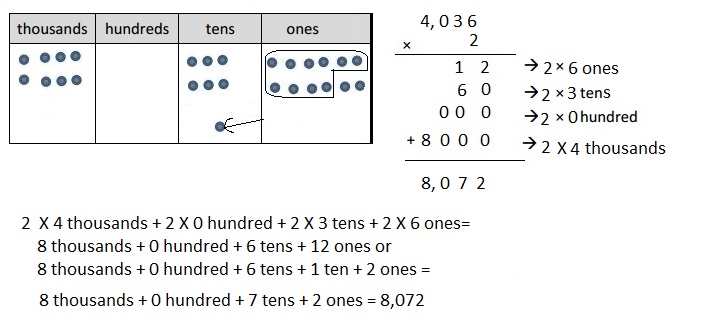
Explanation:
Represented the following expression 2 X 4,036 = 8,072 with disks, regrouped as necessary and recorded the partial products vertically as shown above.
c. 3 × 2,546
Answer:
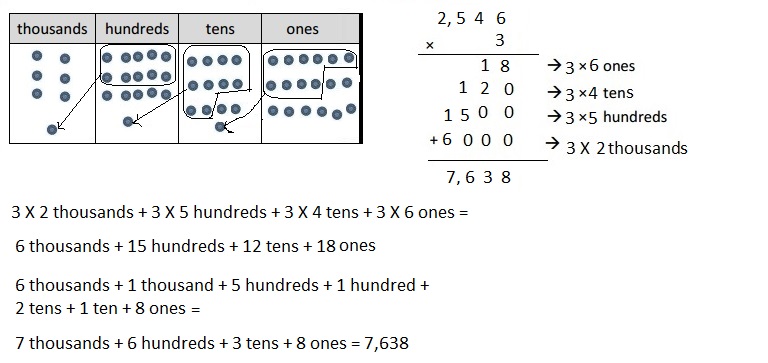
Explanation:
Represented the following expression 3 X 2,546 = 7,638 with disks, regrouped as necessary and recorded the partial products vertically as shown above.
d. 3 × 1,407
Answer:
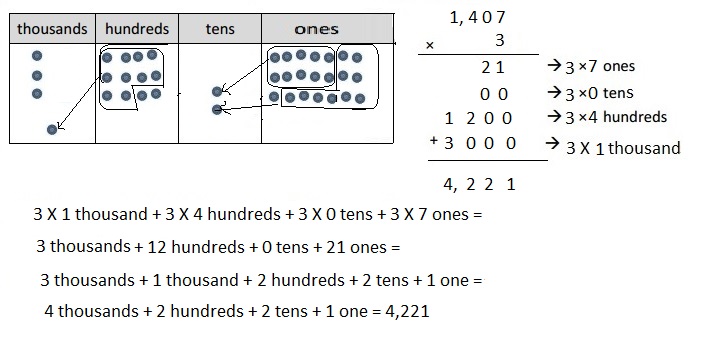 Explanation:
Explanation:
Represented the following expression 3 X 1,407 = 4,221 with disks, regrouped as necessary and recorded the partial products vertically as shown above.
Question 3.
Every day at the bagel factory, Cyndi makes 5 different kinds of bagels. If she makes 144 of each kind, what is the total number of bagels that she makes?
Answer:
Total number of bagels Cyndi makes are 720 every day,
Explanation:
Given every day at the bagel factory, Cyndi makes 5 different kinds of bagels. If she makes 144 of each kind,
The total number of bagels Cyndi makes are 5 X 144 = 720 every day.
Eureka Math Grade 4 Module 3 Lesson 8 Exit Ticket Answer Key
Represent the following expressions with disks, regrouping as necessary. To the right, record the partial products vertically.
Question 1.
4 × 513
Answer:
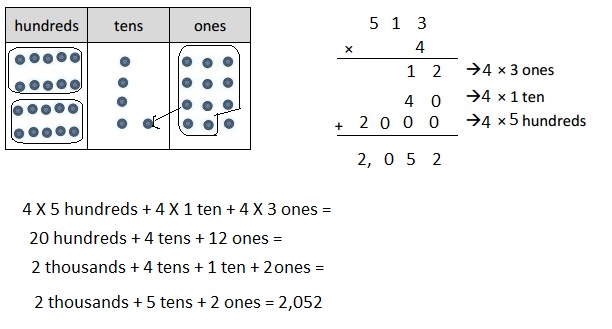
Explanation:
Represented the following expression 4 X 513 = 2,052 with disks, regrouped as necessary and recorded the partial products vertically as shown above.
Question 2.
3 × 1,054
Answer:
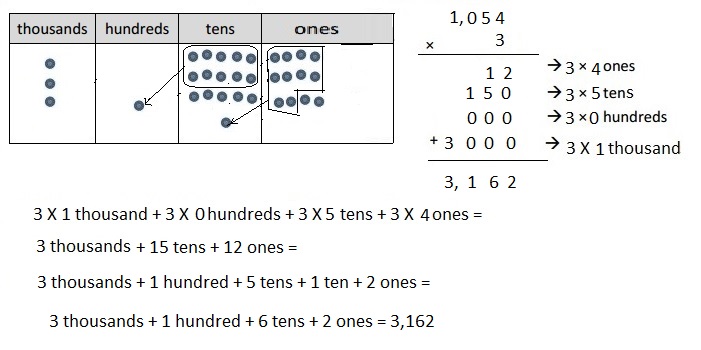
Explanation:
Represented the following expression 3 X 1,054 = 3,162 with disks, regrouped as necessary and recorded the partial products vertically as shown above.
Eureka Math Grade 4 Module 3 Lesson 8 Homework Answer Key
Question 1.
Represent the following expressions with disks, regrouping as necessary, writing a matching expression, and recording the partial products vertically as shown below.
a. 2 × 424
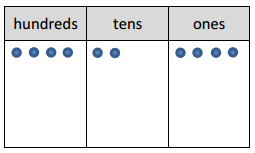
2 × ___ ________ + 2 × ___ _____ + 2 × ___ ones
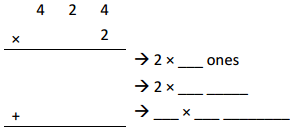
Answer:
Explanation:
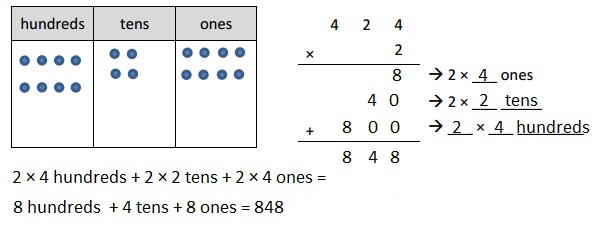
Represented the following expression 2 X 424 with disks, regrouped as necessary. Wrote a matching expression 2 X 424 = 848 and recorded the partial products vertically as shown above.
b. 3 × 424
Answer:
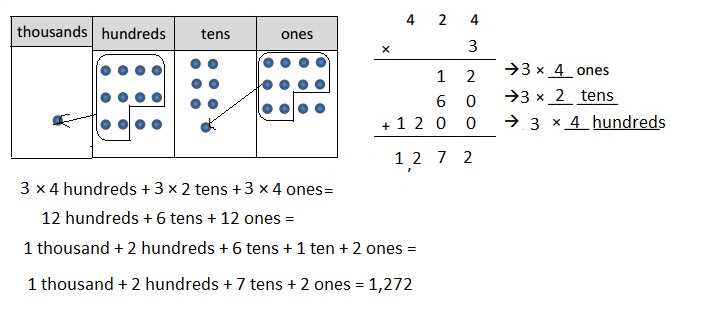
Explanation:
Represented the following expression 3 X 424 with disks, regrouped as necessary. Wrote a matching expression 3 X 424 = 1,272
and recorded the partial products vertically as shown above.
c. 4 × 1,424
Answer:

Explanation:
Represented the following expression 4 X 1,424 with disks, regrouped as necessary. Wrote a matching expression 4 X 1,424 = 5,696
and recorded the partial products vertically as shown above.
Question 2.
Represent the following expressions with disks, using either method shown in class, regrouping as necessary. To the right, record the partial products vertically.
a. 2 × 617
Answer:
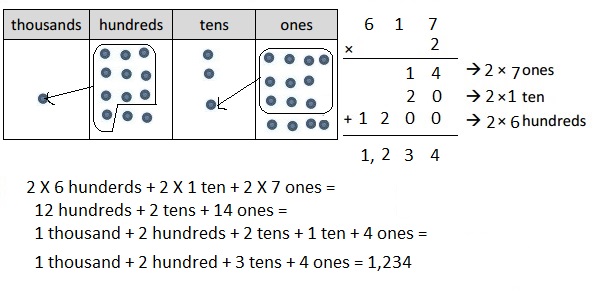
Explanation:
Represented the following expression 2 X 617 with disks, regrouped as necessary. Wrote a matching expression 2 X 617 = 1,234
and recorded the partial products vertically as shown above.
b. 5 × 642
Answer:
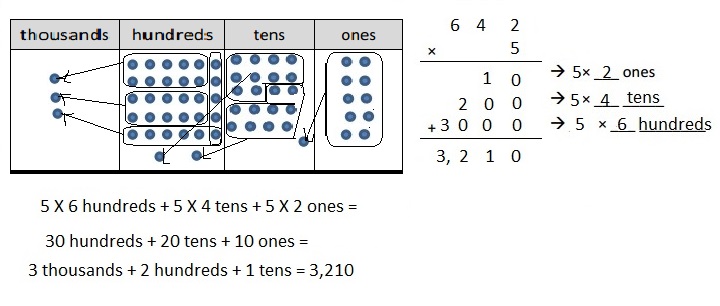
Explanation:
Represented the following expression 5 X 642 with disks, regrouped as necessary. Wrote a matching expression 5 X 642 = 3,210
and recorded the partial products vertically as shown above.
c. 3 × 3,034
Answer:
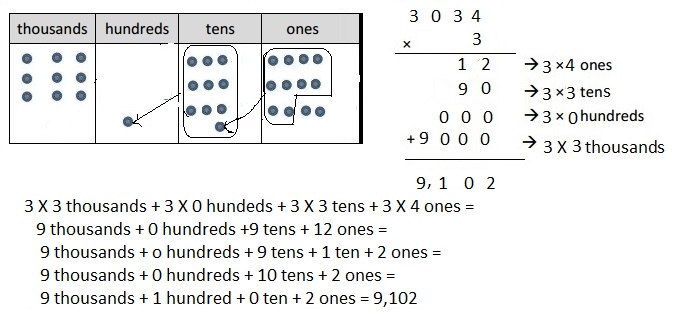
Explanation:
Represented the following expression 3 X 3,034 with disks, regrouped as necessary. Wrote a matching expression 3 X 3,034 = 9,102
and recorded the partial products vertically as shown above.
Question 3.
Every day, Penelope jogs three laps around the playground to keep in shape. The playground is rectangular with a width of 163 m and a length of 320 m.
a. Find the total amount of meters in one lap.
Answer:
The total amount of meters in one lap is 52,160 square meters,
Explanation:
Given the playground is rectangular with a width of 163 m and a length of 320 m
So the total area of the playground is 163 m X 320 m = 52,160 square meters.
Therefore the total amount of meters in one lap is 52,160 square meters Penelope jogs.
b. Determine how many meters Penelope jogs in three laps.
Answer:
Penelope jogs 1,56,480 square meters in three laps,
Explanation:
Given every day, Penelope jogs three laps around the playground to keep in shape. The playground is rectangular with a width of 163 m and a length of 320 m
so total area of the rectangular playground is 163 m X 320 m = 52,160 square meters
Now for 3 laps it is 3 X 52,160 sq mt = 1,56,480 square meters.