Engage NY Eureka Math Geometry Module 4 Lesson 3 Answer Key
Eureka Math Geometry Module 4 Lesson 3 Example Answer Key
Example 1.
Consider the rectangular region:
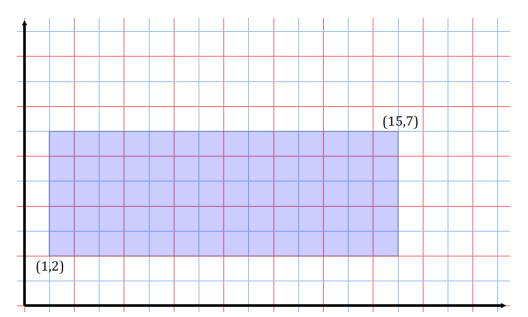
a. Does a line of slope 2 passing through the origin intersect this rectangular region? If so, which boundary points of the rectangle does it intersect? Explain how you know.
Answer:
Yes, it intersects twice, at (1, 2) and (3.5, 7). Student justification may vary. One response may include the use of the algebraic equation y = 2x, or students may create a table of values using their understanding of slope and compare the y – values of their table against the y – values of the boundary points of the rectangle.
b. Does a line of slope \(\frac{1}{2}\) passing through the origin intersect this rectangular region? If so, which boundary points of the rectangle does it intersect?
Answer:
Yes, it intersects twice, at (4, 2) and (14, 7).
c. Does a line of slope \(\frac{1}{3}\) passing through the origin intersect this rectangular region? If so, which boundary points of the rectangle does it intersect?
Answer:
Yes, it intersects twice, at (6, 2) and (15, 5).
d. A line passes through the origin and the lower right vertex of the rectangle. Does the line pass through the interior of the rectangular region or the boundary of the rectangular region? Does the line pass through both?
Answer:
The line passes through the boundary of the rectangular region.
e. For which values of m would a line of slope m through the origin intersect this region?
Answer:
\(\frac{2}{15}\) ≤ m ≤ 7
f. For which values of m would a line of slope m through the point (0, 1) intersect this region?
Answer:
\(\frac{1}{15}\) ≤ m ≤ 6
Example 2.
Consider the triangular region in the plane given by the triangle with vertices A(0, 0), B(2, 6), and C(4, 2).
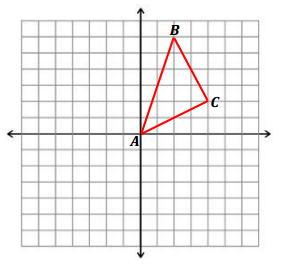
a. The horizontal line y = 2 intersects this region. What are the coordinates of the two boundary points it intersects? What is the length of the horizontal segment within the region along this line?
Answer:
The coordinates are (\(\frac{2}{3}\), 2) and (4, 2); the length of the segment is 3 \(\frac{1}{3}\) units.
b. Graph the line 3x – 2y = 5. Find the points of intersection with the boundary of the triangular region, and label them as X and Y.
Answer:
The points of intersection are (\(\frac{5}{2}\), \(\frac{5}{4}\)) and (\(\frac{25}{7}\), \(\frac{20}{7}\)).
c. What is the length of the \(\overline{X Y}\)?
ans;
d[(\(\frac{5}{2}\), \(\frac{5}{4}\)), (\(\frac{25}{7}\), \(\frac{20}{7}\))] = \(\sqrt{\left(\frac{25}{7} – \frac{5}{2}\right)^{2} + \left(\frac{20}{7} – \frac{5}{4}\right)^{2}}\) ≈ 1.9
d. A robot starts at position (1, 3) and moves vertically downward toward the x – axis at a constant speed of 0.2 units per second. When will it hit the lower boundary of the triangular region that falls in its vertical path?
Answer:
\(\frac{2.5 \text { units }}{0.2 \frac{\text { units }}{\text { sec }}}\) = 12
Eureka Math Geometry Module 4 Lesson 3 Exercise Answer Key
Opening Exercise
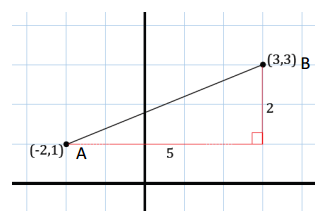
How can we use the Pythagorean theorem to find the length of \(\overline{A B}\), or in other words, the distance between A( – 2, 1) and B(3, 3)? Find the distance between A and B.
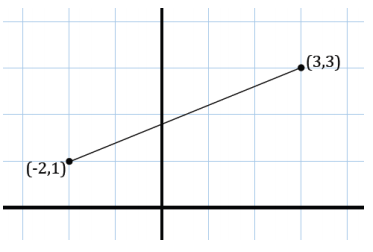
Answer:
The distance between A and B is \(\sqrt{29}\). By treating the length between the provided points as the hypotenuse of a right triangle, we can build a right triangle and determine the leg lengths in order to apply the Pythagorean theorem and calculate the length of the hypotenuse, which is the length we were trying to find.
Exercise
Consider the given rectangular region:
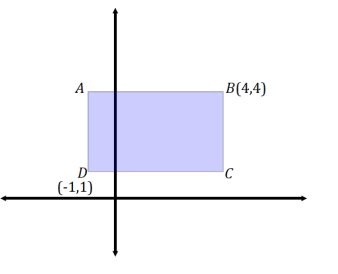
a. Draw lines that pass through the origin and through each of the vertices of the rectangular region. Do each of the four lines cross multiple points in the region? Explain.
Answer:
Out of the four lines that pass through the origin and each of the vertices, only the lines that pass through A and B pass through multiple points in the region. The lines that pass through C and D do not intersect any other points belonging to the region.
b. Write the equation of a line that does not intersect the rectangular region at all.
Answer:
Responses will vary; one example is x = – 2.
c. A robot is positioned at D and begins to move in a straight line with slope m = 1. When it intersects with a boundary, it then reorients itself and begins to move in a straight line with a slope of m = – \(\frac{1}{2}\). What is the location of the next intersection the robot makes with the boundary of the rectangular region?
Answer:
(4, 3)
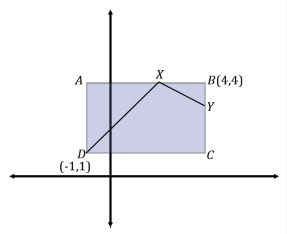
d. What is the approximate distance of the robot’s path in part (c)?
Answer:
distance(\(\overline{D X}\)) + distance(\(\overline{X Y}\)) = distance(path)
\(\sqrt{( – 1 – 2)^{2} + (1 – 4)^{2}}\) + \(\sqrt{(2 – 4)^{2} + (4 – 3)^{2}}\) ≈ 6.5
Eureka Math Geometry Module 4 Lesson 3 Problem Set Answer Key
Question 1.
A line intersects a triangle at least once, but not at any of its vertices. What is the maximum number of sides that a line can intersect a triangle? Similarly, a square? A convex quadrilateral? A quadrilateral, in general?
Answer:
For any convex polygon, the maximum number of sides a line can intersect the polygon is 2. For a general quadrilateral, the line could intersect up to all 4 sides.
Question 2.
Consider the rectangular region:
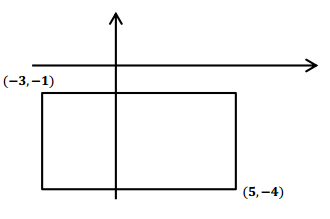
a. What boundary points does a line through the origin with a slope of – 2 intersect? What is the length of the segment within this region along this line?
Answer:
It intersects at (\(\frac{1}{2}\), – 1) and (2, – 4); the length is approximately 3.35 units.
b. What boundary points does a line through the origin with a slope of 3 intersect? What is the length of the segment within this region along this line?
Answer:
It intersects at ( – \(\frac{1}{3}\), – 1) and ( – 1\(\frac{1}{3}\), – 4); the length is approximately 3.2 units.
c. What boundary points does a line through the origin with a slope of – \(\frac{1}{5}\) intersect?
Answer:
It intersects at (5, – 1) only.
d. What boundary points does a line through the origin with a slope of \(\frac{1}{4}\) intersect?
Answer:
The line does not intersect the rectangular region.
Question 3.
Consider the triangular region in the plane given by the triangle ( – 1, 3), (1, – 2), and ( – 3, – 3).
a. The horizontal line y = 1 intersects this region. What are the coordinates of the two boundary points it intersects? What is the length of the horizontal segment within the region along this line?
Answer:
It intersects at ( – 1 \(\frac{2}{3}\), 1) and ( – \(\frac{1}{5}\), 1); the length is approximately 1.47 units.
b. What is the length of the section of the line 2x + 3y = – 4 that lies within this region?
Answer:
The length is approximately 3.6 units.
c. If a robot starts at ( – 1, 3) and moves vertically downward at a constant speed of 0.75 units per second, when will it hit the lower boundary of the triangular region?
Answer:
It will hit in approximately 7.3 seconds.
d. If the robot starts at (1, – 2) and moves horizontally left at a constant speed of 0.6 units per second, when will it hit the left boundary of the triangular region?
Answer:
It will hit in approximately 6.1 seconds.
Question 4.
A computer software exists so that the cursor of the program begins and ends at the origin of the plane. A program is written to draw a triangle with vertices A(1, 4), B(6, 2), and C(3, 1) so that the cursor only moves in straight lines and travels from the origin to A, then to B, then to C, then to A, and then back “home” to the origin.
a. Sketch the cursor’s path (i.e., sketch the entire path from when it begins until when it returns “home”).
Answer:
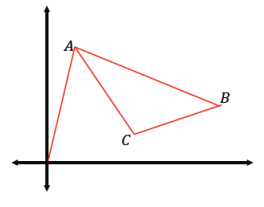
b. What is the approximate total distance traveled by the cursor?
Answer:
\(\sqrt{17}\) + \(\sqrt{29}\) + \(\sqrt{10}\) + \(\sqrt{13}\) + \(\sqrt{17}\) ≈ 20.4
c. Assume the cursor is positioned at B and is moving horizontally toward the y – axis at \(\frac{2}{3}\) units per second.
Answer:
How long will it take to reach the boundary of the triangle?
Equation of \(\overleftrightarrow{A C}\) y = – 1.5x + 5.5
x – coordinate on \(\overleftrightarrow{A C}\)at y = 2: \(\frac{7}{3}\)
Distance from B(6, 2) to (\(\frac{7}{3}\), 2) : \(\frac{11}{3}\) units
Time needed to reach (\(\frac{7}{3}\), 2) : \(\frac{11}{3}\) units ÷ \(\frac{2}{3}\) units/sec = 5.5 sec
Question 5.
An equilateral triangle with side length 1 is placed in the first quadrant so that one of its vertices is at the origin, and another vertex is on the x – axis. A line passes through the point half the distance between the endpoints on one side and half the distance between the endpoints on the other side.
a. Draw a picture that satisfies these conditions.
Answer:
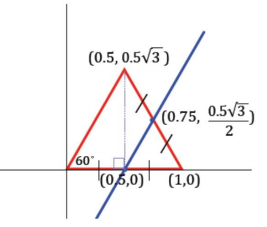
Students can use trigonometry to find the vertex at . Then, average the coordinates of the endpoints, and (0.75, \(\frac{0.5 \sqrt{3}}{2}\)) can be established.
b. Find the equation of the line that you drew.
Answer:
The line through (0.5, 0) and (0.75, \(\frac{0.5 \sqrt{3}}{2}\)) is
y = \(\sqrt{3}\) x – 0.5\(\sqrt{3}\).
Eureka Math Geometry Module 4 Lesson 3 Exit Ticket Answer Key
Question 1.
Consider the rectangular region:
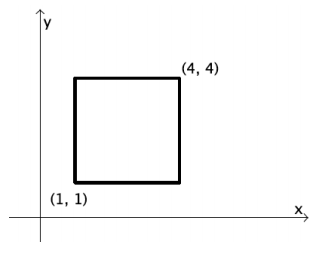
a. Does a line with slope \(\frac{1}{2}\) passing through the origin intersect this region? If so, what are the boundary points it intersects? What is the length of the segment within the region?
Answer:
Yes, it intersects at (2, 1) and (4, 2); the length is approximately 2.24 units.
b. Does a line with slope 3 passing through the origin intersect this region? If so, what are the boundary points it intersects?
Answer:
Yes, it intersects at (1, 3) and (1\(\frac{1}{3}\) , 4).