Engage NY Eureka Math Geometry Module 4 Lesson 10 Answer Key
Eureka Math Geometry Module 4 Lesson 10 Opening Exercise Answer Key
Find the area of the triangle given. Compare your answer and method to your neighbor’s, and discuss differences.
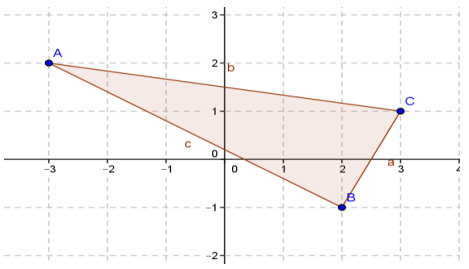
Answer:
Shoelace Formula:
Coordinates: A(-3, 2), B(2, -1), C(3, 1)
Area Calculation:
\(\frac{1}{2}\)((-3) ∙ (-1) + 2 ∙ 1 + 3 ∙ 2 – 2 ∙ 2 – (-1) ∙ 3 – 1 ∙ (3))
Area: 6.5 square units
Decomposition:
Area of Rectangle: 6 units 3 units = 18 square units
Area of Left Rectangle: 7 ∙ 5 square units
Area of Bottom Right Triangle: 1 square unit
Area of Top Right Triangle: 3 square units
Area of Shaded Triangle: 18 – 7.5 – 1 – 3 = 6.5
Area is 6.5 square units.
Eureka Math Geometry Module 4 Lesson 10 Exercise Answer Key
Exercise 1.
Given rectangle ABCD:
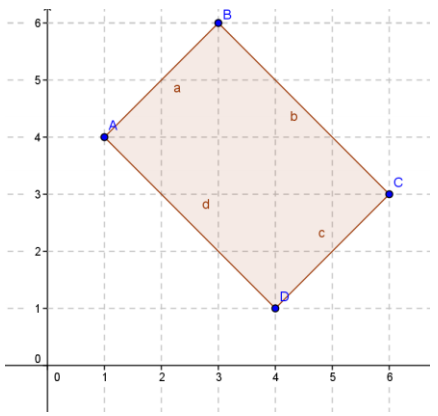
a. Identify the vertices.
Answer:
A (1, 4), B (3,6), C (6, 3), D (4, 1)
b. Find the perimeter using the distance formula.
Answer:
Approximately 14.14 units
c. Find the area using the area formula.
Answer:
(√8) (√8) = 12
The area is 12 square units.
d. List the vertices starting with A moving counterclockwise.
Answer:
A (1, 4), D(4, 1), C(6, 3), B(3, 6)
e. Verify the area using the shoelace formula.
Answer:
\(\frac{1}{2}\)(1 ∙ 1 + 4 ∙ 3 + 6 ∙ 6 + 3 ∙ 4 – 4 ∙ 4 – 1 ∙ 6 – 3 ∙ 3 – 6 ∙ 1) = 12
The area is 12 square units.
Exercise 2.
Calculate the area and perimeter of the given quadrilateral using the shoelace formula.
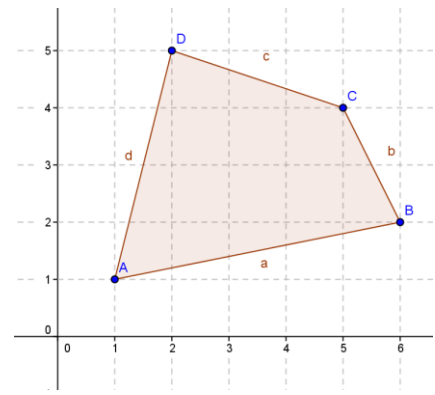
Answer:
Area = \(\frac{1}{2}\)(1 ∙ 2 + 6 ∙ 4 + 5 ∙ 5 + 2 ∙ 1 – 1 ∙ 6 – 2 ∙ 5 – 4 ∙ 2 – 5 ∙ 1) = 12
The area is 12 square units.
The perimeter is approximately 14.62 units
Exercise 3.
Break up the pentagon to find the area using Green’s theorem. Compare your method with a partner.
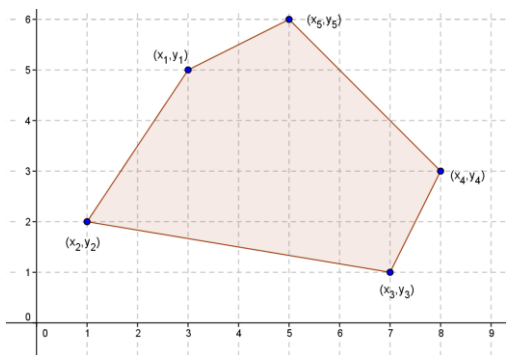
Answer:
Methods will vary. If broken into a triangle with vertices (x1, y1), (x2, y2), and (x3, y3), and a quadrilateral with vertices (x1, y1), (x3, y3), (x4, y4), and (x5, y5), the formula would be,
\(\frac{1}{2}\)(x1y2 + x2y3 + x3y1 – y1x2 – y2x3 – y3x1) + \(\frac{1}{2}\)(x3y4 + x4y5 + x5y1 + x1y3 – y3x4 + y4x5 + y5x1 + y1x3).
The area is 20.5 square units.
Exercise 4.
Find the perimeter and the area of the quadrilateral with vertices A(-3, 4), B(4, 6), C(2, -3), and D(-4, -4).
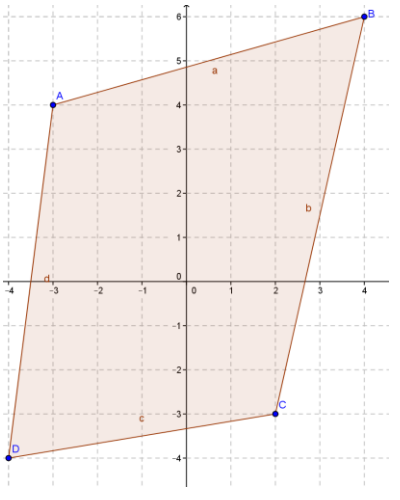
Answer:
Perimeter 30.64 units
Area = \(\frac{1}{2}\)((-3) ∙ (-4) + (-4) ∙ -3 + 2 ∙ 6 + 4 ∙ 4 – 4 ∙ (-4) – (-4) ∙ 2 – (-3) ∙ 4 – 6 ∙ (-3)) = 53
The area is 53 square units.
Exercise 5.
Find the area of the pentagon with vertices A(5, 8), B(4, -3), C(-1, -2), D(-2, 4), and E(2, 6).
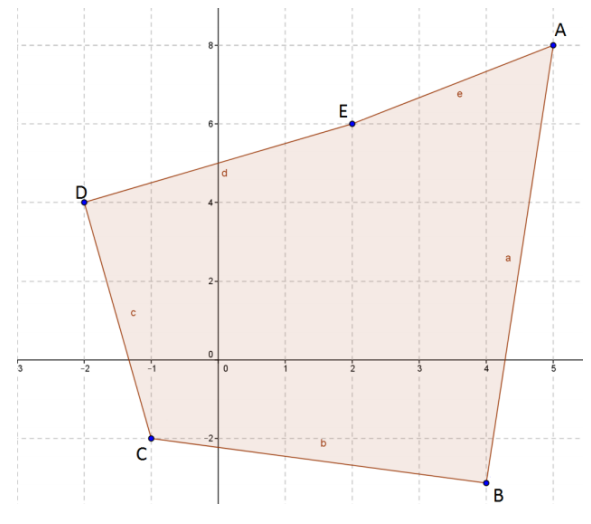
Answer:
Area:
\(\frac{1}{2}\)(5 ∙ 6 + 2 ∙ 4 + (-2) ∙ (-2) + (-1) ∙ (-3) + 4 ∙ 8 – 8 ∙ 2 – 6 ∙ (-2) – 4 ∙ (-1) – (-2) ∙ 4 – (-3) ∙ 5 = 50
The area is 50 square units.
Exercise 6.
Find the area and perimeter of the hexagon shown.
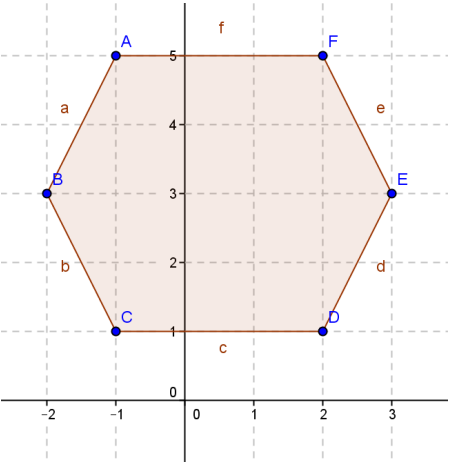
Answer:
Area:
\(\frac{1}{2}\)(-1 ∙ 3) + (-2) ∙ 1 + (-1) ∙ 1 + 2 ∙ 3 + 3 ∙ 5 + 2 ∙ 5 – 5 ∙ (-2) – 3 ∙ (-1) – 1 ∙ 2 – 1 ∙ 3 – 3 ∙ 2 – 5 ∙ (-1)) = 16
The area is 16 square units.
The perimeter of the hexagon is approximately 14.94 units.
Eureka Math Geometry Module 4 Lesson 10 Problem Set Answer Key
Question 1.
Given triangle ABC with vertices (7, 4), (1, 1), and (9, 0):
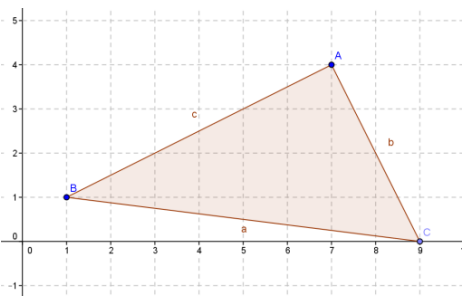
a. Calculate the perimeter using the distance formula.
Answer:
The perimeter is approximately 19. 24 units.
b. Calculate the area using the traditional area formula.
Answer:
Area: (√45) (√20) = 15
c. Calculate the area using the shoelace formula.
Answer:
Area: (7 ∙ 1 + 1 ∙ 0 + 9 ∙ 4 – 4 ∙ 1 – 1 ∙ 9 – 0 ∙ 7) = 15
d. Explain why the shoelace formula might be more useful and efficient if you were just asked to find the area.
Answer:
To use the shoelace formula, all you need are the coordinates of the vertices; you would not have to use the distance formula.
Question 2.
Given triangle ABC and quadrilateral DEFG, describe how you would find the area of each and why you would choose that method, and then find the areas.
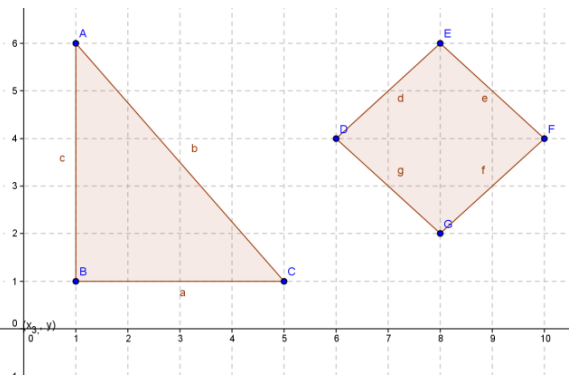
Answer:
The triangle is a right triangle, and the length and height can be read from the graph, so it would be easiest to find its area by the traditional area formula. Area: 10 square units
To find the area of the quadrilateral, I would use the shoelace formula because the traditional formula would require use of the distance formula first. Area: 8 square units
Question 3.
Find the area and perimeter of quadrilateral ABCD with vertices A(6, 5), B(2, -4), C(-5, 2), and D(-3, 6).
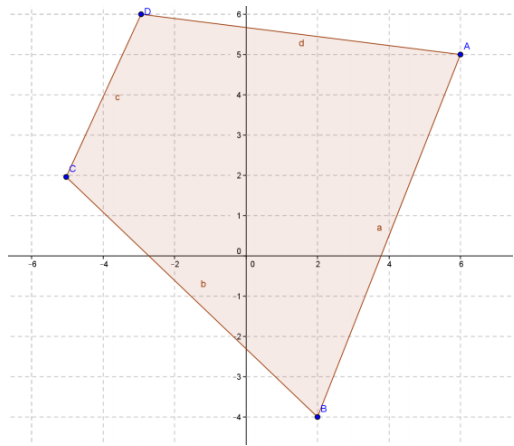
Answer:
The area is 62.5 square units.
The perimeter of quadrilateral ABCD is approximately 32.60 units.
Question 4.
Find the area and perimeter of pentagon ABCDE with vertices A(2, 6), 8(7,2), C(3, -4), D(-3, -2), and E(-2, 4).
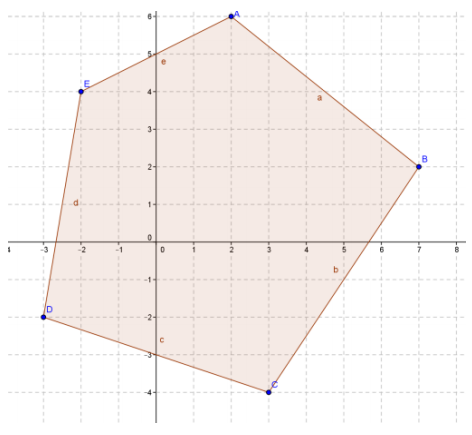
Answer:
The area is 63 square units.
The perimeter of pentagon ABCDE is approximately 30.49 units.
Question 5.
Show that the shoelace formula (Green’s theorem) used on the trapezoid shown confirms the traditional formula for the area of a trapezoid \(\frac{1}{2}\)(b1 + b2) h.
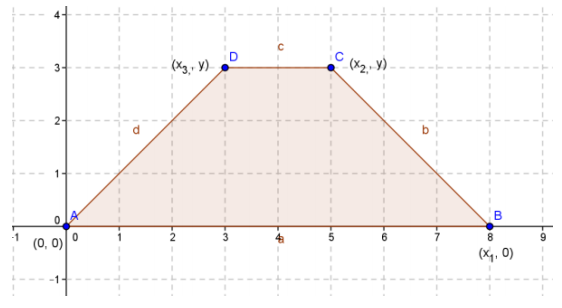
Answer:
Traditional using coordinates listed:
b1 = x1, b2 = x2 – x3, h = y
\(\frac{1}{2}\) (x1 + x2 – x3) ∙ y
Shoelace formula:
\(\frac{1}{2}\) (0 ∙ 0 + x1 ∙ y + x2 ∙ y + x3 ∙ 0 – 0 ∙ x1 – 0 ∙ x2 – y ∙ x3 – y ∙ 0) = \(\frac{1}{2}\)(x1 ∙ y + x2 ∙ y – x3 ∙ y)
= \(\frac{1}{2}\)(x1 + x2 – x3) ∙ y
Eureka Math Geometry Module 4 Lesson 10 Exit Ticket Answer Key
Cory is using the shoelace formula to calculate the area of the pentagon shown. The pentagon has vertices A(4, 7), B(2, 5), C(1, 2), D(3, 1), and E(5, 3). His calculations are below. Toya says his answer can’t be correct because the area in the region ¡s more than 2 square units. Can you identify and explain Cory’s error and help him calculate the correctarea?
Cory’s work:
\(\frac{1}{2}\)(4 ∙ 5 + 2 ∙ 2 + 1 ∙ 1 + 3 ∙ 3 – 7 ∙ 2 – 5 ∙ 1 – 2 ∙ 3 – 1 ∙ 5) = 2
The area is 2 square units.
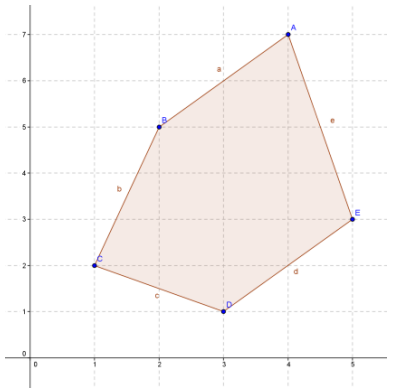
Answer:
Cory left out the last pair of calculations ¡n both directions. He did not return to his starting point. The calculation should be\(\frac{1}{2}\)(4 ∙ 5 + 2 ∙ 2 + 1 ∙ 1 + 3 ∙ 3 + 5 ∙ 7 – 7 ∙ 2 – 5 ∙ 1 – 2 ∙ 3 – 1 ∙ 5 – 3 ∙ 4) = 13.5
The area of the pentagon is 13.5 square units.