Engage NY Eureka Math Geometry Module 4 Lesson 11 Answer Key
Eureka Math Geometry Module 4 Lesson 11 Example Answer Key
A parallelogram with base of length b and height h can be situated in the coordinate plane, as shown. Verify that the shoelace formula gives the area of the parallelogram as bh.
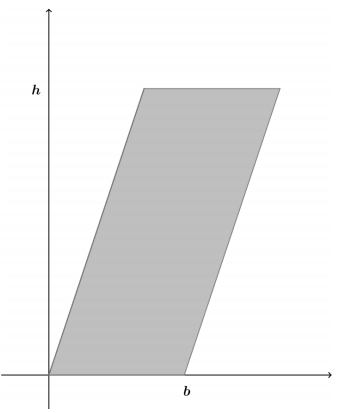
Answer:
→ What is the area of a parallelogram?
Base × height
→ The distance from the y-axis to the top left vertex is some number x. What are
the coordinates of that vertex?
(x, h)
→ Can you determine the coordinates of the top right vertex? What do we know about opposite sides of a parallelogram?
They must be equal.
→ What is the length of the bottom side?
b units
→ So what is the length of the top side?
b units
→ The bottom side starts at the origin (where x = 0); where does the top side start? Hint: What is the x-coordinate of the top left vertex?
x
→ So, if the length is b units, what would the x-coordinate of the top right vertex be?
x + b
→ So, what are the coordinates of the top right vertex?
(x + b, h)
→ List the coordinates of the vertices starting at the origin and moving counterclockwise.
(0, 0), (x, h), (x + b, h), and (b, 0)
→ Use the shoelace formula (Green’s theorem) to find the area moving counterclockwise.
\(\frac{1}{2}\)(0 ∙ 0 + b ∙ h + (x + b) ∙ h + x ∙ 0 – 0 ∙ b – 0 ∙ ( (x + b) – h ∙ x – h ∙ 0) =
\(\frac{1}{2}\)(b ∙ h + x ∙ h + b ∙ h – h ∙ x) = \(\frac{1}{2}\)(2(b ∙ h)) = b ∙ h
Example 2.
A triangle with base b and height h can be situated in the coordinate plane, as shown. According to Green’s theorem, what is the area of the triangle?
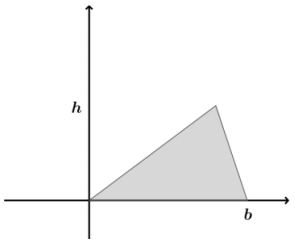
Answer:
Let students try to do this problem on their own following the steps used above. Scaffold with the following questions as necessary.
→ What is the area of a triangle?
base × height
→ Let the distance from the y-axis to the top vertex be some number x. What are the coordinates of that vertex?
(x, h)
→ List the coordinates of the vertices starting at the origin and moving clockwise.
(0, 0), (x, h), and (b, 0)
→ Use the shoelace formula (Green’s theorem) to find the area moving counterclockwise.
\(\frac{1}{2}\)(0 ∙ 0 + b ∙ h + x ∙ 0 – 0 ∙ b – 0 ∙ x – h ∙ 0) = \(\frac{1}{2}\)(b ∙ h)
→ Summarize what you have learned so far with a partner.
We have verified well-known formulas using Green’s theorem.
Eureka Math Geometry Module 4 Lesson 11 Opening Exercise Answer Key
Graph the following
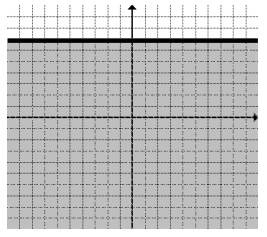
a. y ≤ 7
Answer:
b. x > – 3

Answer:
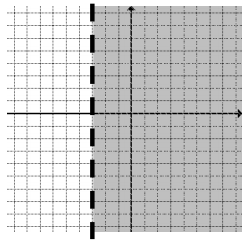
c. y < \(\frac{1}{2}\)x – 4

Answer:
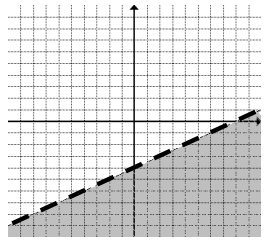
d. y ≥ –\(\frac{2}{3}\)x + 5

Answer:
Eureka Math Geometry Module 4 Lesson 11 Exercise Answer Key
Exercise 1.
A quadrilateral region is defined by the system of inequalities below:
y ≤ x + 6 y ≤ – 2x + 12 y ≥ 2x – 4 y ≥ – x + 2
a. Sketch the region.

Answer:

b. Determine the vertices of the quadrilateral.
Answer:
(2, 8), (4, 4), (2, 0), (- 2, 4) Ask students how they can verify the intersection points. (By showing that each set of coordinates satisfies the equations of both intersecting lines that determine the vertex.)
c. Find the perimeter of the quadrilateral region.
Answer:
Approximately 20.26 units
d. Find the area of the quadrilateral region.
Answer:
24 square units
Exercise 2.
A quadrilateral region is defined by the system of Inequalities below:
y ≤ x + 5 y ≥ x – 4 y ≤ 4 y ≥ –\(\frac{5}{4}\)x – 4
a. Sketch the region.

Answer:
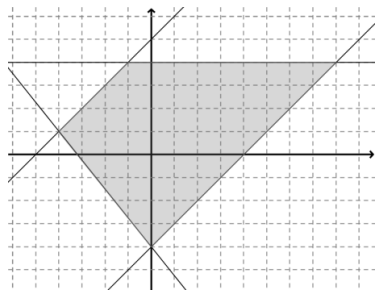
b. Determine the vertices of the quadrilateral.
Answer:
(- 4, 1), (-1, 4), (8, 4), (0, – 4)
c. Which quadrilateral is defined by these inequalities? How can you prove your conclusion?
Answer:
A trapezoid is defined by these ine qualities. We can prove that one pair of opposite sides is parallel.
d. Find the perimeter of the quadrilateral region.
Answer:
The perimeter is approximately 30.96 units.
e. Find the area of the quadrilateral region.
Answer:
The area of the quadrilateral region is 49.5 square units.
Eureka Math Geometry Module 4 Lesson 11 Problem Set Answer Key
Question 1.
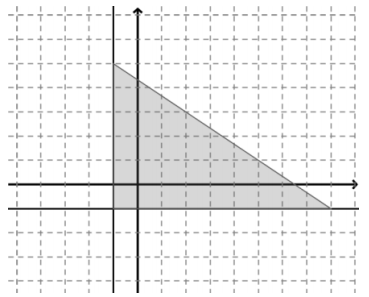
Answer:
y ≥ – 1, x ≥ – 1, y ≤ –\(\frac{2}{3}\)x + \(\frac{13}{3}\)
Question 2.
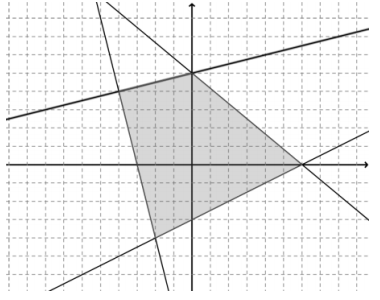
Answer:
y ≥ \(\frac{1}{2}\)x – 3 y ≤ –\(\frac{5}{6}\)x + 5 y ≤ \(\frac{1}{4}\)x + 5 y ≥ -4x – 12
For Problems 3-5 below, a triangular or quadrilateral region Is defined W the system of Inequalities listed.
a. Sketch the region.
b. Determine the coordinates of the vertices.
c. Find the perimeter of the region rounded to the nearest hundredth If necessary.
d. Find the area of the region rounded to the nearest tenth If necessary.
Question 3.
8x – 9y ≥ – 2 2 x + y ≤ 10 5x – 12y ≤ – 1
Answer:
a.
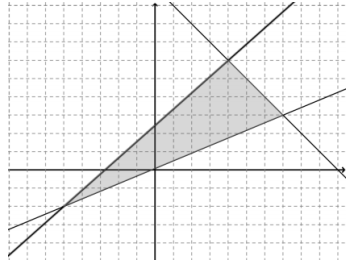
b. (4, 6), (7, 3), (-5, -2)
c. Approximately 29.28 units
d. 25.5 square units
Question 4.
x + 3y ≥ 0 4x – 3y ≥ 0 2x + y ≤ 10
Answer:
a.
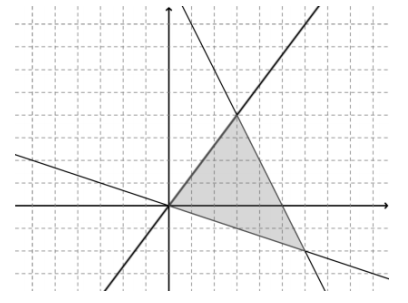
b. (3, 4), (6, -2), (0, 0)
c. Approximately 18.03 units
d. 15 square units
Question 5.
2x – 5y ≥ – 14 3x + 2y ≤ 17 2x – y ≤ 9 x + y ≥ 0
Answer:
a.
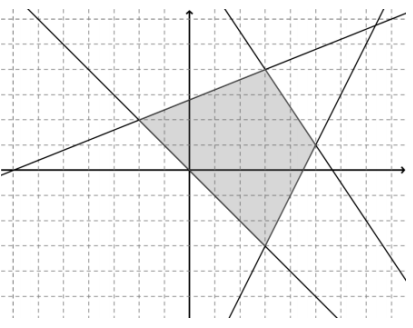
b. (3, 4), (5, 1), (3, – 3), (-2, 2)
c. Approximately 20.53 units
d. 24.5 square units
Eureka Math Geometry Module 4 Lesson 11 Exit Ticket Answer Key
A quadrilateral region is defined by the system of inequalities below:
y ≤ 5 y y ≥ – 3 y ≤ 2x + 1 y ≥ 2x – 7
Question 1.
Sketch the region.
Answer:
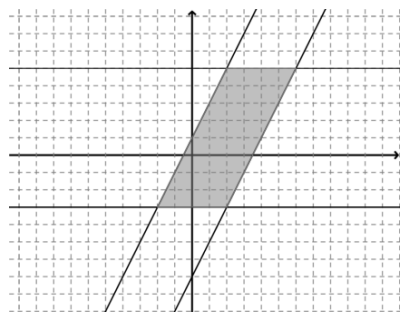
Question 2.
Determine the coordinates of the vertices.
Answer:
(2,5), (6, 5), (2, – 3), (- 2, – 3)
Question 3.
Find the area of the quadrilateral region.
Answer:
32 square units