Engage NY Eureka Math Geometry Module 2 Lesson 32 Answer Key
Eureka Math Geometry Module 2 Lesson 32 Example Answer Key
Example 1.
A surveyor needs to determine the distance between two points A and B that lie on opposite banks of a river. A point C is chosen 160 meters from point A, on the same side of the river as A. The measures of ∠BAC and ∠ACB are 41° and 55°, respectively. Approximate the distance from A to B to the nearest meter.
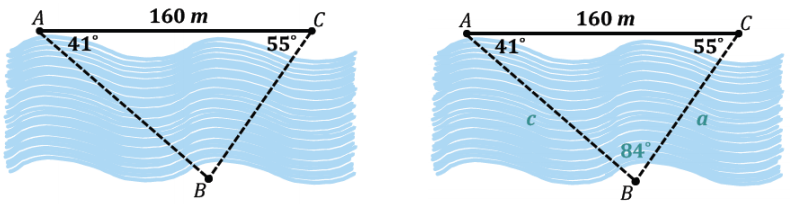
Answer:
→ What measurement can we add to the diagram based on the provided information?
The measurement of ∠B must be 84° by the triangle sum theorem.
→ Use the law of sines to set up all possible ratios applicable to the diagram.
\(\frac{\sin 41}{a}\) = \(\frac{\sin 84}{160}\) = \(\frac{\sin 55}{c}\)
→ Which ratios will be relevant to determining the distance from A to B?
\(\frac{\sin 84}{160}\) = \(\frac{\sin 55}{c}\)
→ Solve for c.
c = \(\frac{160 \sin 55}{\sin 84}\)
c = 132
The distance from A to B is 132 m.
Example 2.
Our friend the surveyor from Example 1 is doing some further work. He has already found the distance between points A and B (from Example 1). Now he wants to locate a point D that is equidistant from both A and B and on the same side of the river as A. He has his assistant mark the point D so that ∠ABD and ∠BAD both measure 75°. What is the distance between D and A to the nearest meter?
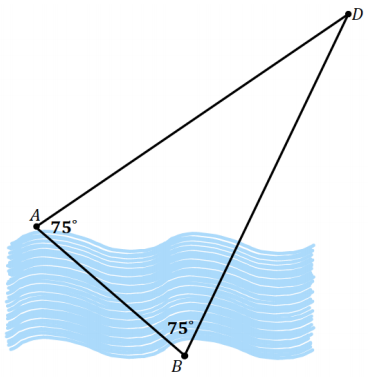
Answer:
→ What do you notice about ∆ ABD right away?
∆ ABD must be an isosceles triangle since it has two angles of equal measure.
→ We must keep this in mind going forward. Add all relevant labels to the diagram.
Students should add the distance of 132 m between A and B and add the label of a and b to the appropriate sides.
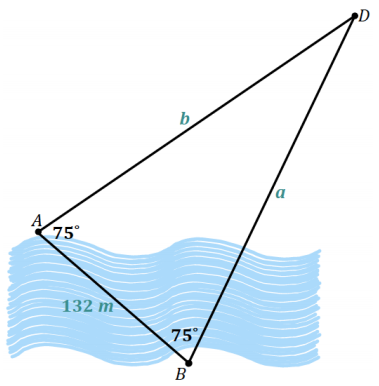
→ Set up an equation using the law of cosines. Remember, we are trying to find the distance between D and or, as we have labeled it, b.
b2 = 1322 + a2 – 2(132)(a) cos 75
→ Recall that this is an isosceles triangle; we know that a = b. To reduce variables, we will substitute b for a.
Rewrite the equation, and solve for b.
Sample solution:
b2 = 1322 + (b)2 – 2(132) (b) cos 75
b2 = 1322 + (b)2 – 264(b) cos 75
0 = 1322 – 264(b)cos 75
264(b) cos 75 = 1322
b = \(\frac{132^{2}}{264 \cos 75}\)
b ≈ 255 m
Eureka Math Geometry Module 2 Lesson 32 Opening Exercise Answer Key
a. Find the length of d and e.
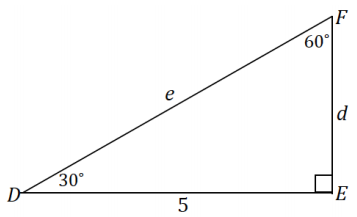
Answer:
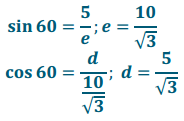
b. Find the lengths of x and y. How is this different from part (a)?
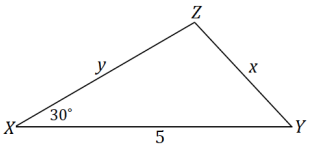
Answer:
Accept any reasonable answer explaining that the triangle is not a right triangle; therefore, the trigonometric ratios used in part (a) are not applicable here.
Eureka Math Geometry Module 2 Lesson 32 Exercise Answer Key
Exercise 1.
In ∆ ABC, m∠A 30, a = 12, and b = 10. Find sin∠B. Include a diagram in your answer.
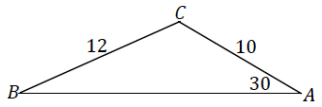
Answer:
\(\frac{\sin 30}{12}=\frac{\sin \angle B}{10}\)
sin ∠B = \(\frac{5}{12}\)
Exercise 2.
A car is moving toward a tunnel carved out of the base of a hill. As the accompanying diagram shows, the top of the hill, H, is sighted from two locations, A and B. The distance between A and B is 250 ft. What is the height, h, of the hill to the nearest foot?
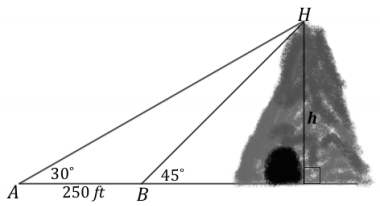
Answer:
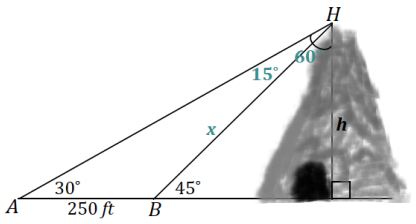
Let x represent BH, in feet. Applying the law of sines,
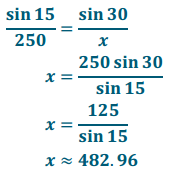
\(\overline{B H}\) is the hypotenuse of a 45 – 45 – 90 triangle whose sides are in the ratio 1: 1: √2, or h: h: h√2.
h√2 = x
h√2 = \(\frac{125}{\sin 15}\)
h = \(\frac{125}{\sin 15 \cdot \sqrt{2}}\)
h ≈ 342
The height of the hill is approximately 324 feet.
Exercise 3.
Parallelogram ABCD has sides of lengths 44 mm and 26 mm, and one of the angles has a measure of 100°.
Approximate the length of diagonal \(\overline{A C}\) to the nearest millimeter.
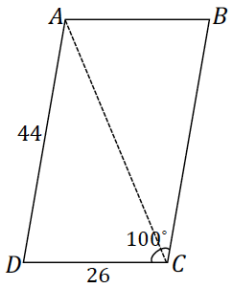
Answer:
In parallelogram ABCD, m∠C = 100°; therefore, m∠D = 80°.
Let d represent the length of \(\overline{A C}\).
d2 = 442 + 262 – 2(44) (26) cos 80
d = 47
The length of \(\overline{A C}\) is 47 millimeters.
Eureka Math Geometry Module 2 Lesson 32 Problem Set Answer Key
Question 1.
Given ∆ ABC, AB = 14, m∠A = 57. 2°, and m∠C = 78. 4°, calculate the measure of angle B to the nearest tenth of a degree, and use the law of sines to find the lengths of \(\overline{A C}\) and \(\overline{B C}\) to the nearest tenth.
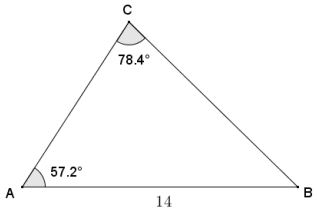
Answer:
By the angle sum of a triangle, m∠B = 44.4°.
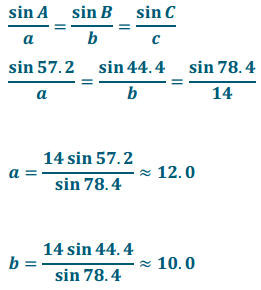
Calculate the area of ∆ ABC to the nearest square unit.
Answer:
Area = \(\frac{1}{2}\) bc sin A
Area = \(\frac{1}{2}\) (10)(14) sin 57.2
Area = 70 sin 57.2
Area ≈ 59
Question 2.
Given ∆ DEF, m∠F = 39°, and EF = 13, calculate the measure of ∠E, and use the law of sines to find the lengths of \(\overline{D F}\) and \(\overline{D E}\) to the nearest hundredth.
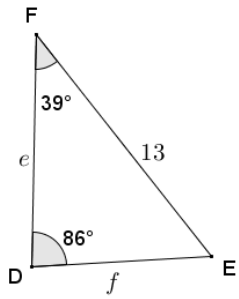
Answer:
By the angle sum of a triangle, m∠E = 55°.
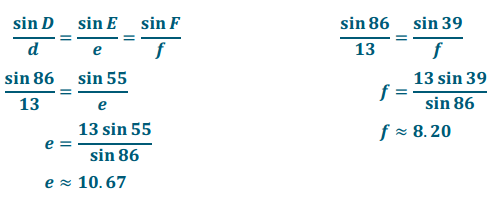
Question 3.
Does the law of sines apply to a right triangle? Based on ∆ ABC, the following ratios were set up according to the law of sines.
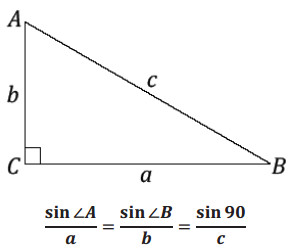
Fill in the partially completed work below:

What conclusions can we draw?
Answer:
The law of sines does apply to a right triangle. We get the formulas that are equivalent to sin ∠A = \(\frac{\text { opp }}{\text { hyp }}\) and sin ∠B = \(\frac{\text { opp }}{\text { hyp }}\) where A and B are the measures of the acute angles of the right triangle.
Question 4.
Given quadrilateral GHKJ, m∠H = 50°, m∠HKG = 80°, mLKGJ = 50°, ∠j is a right angle, and GH = 9 in, use the law of sines to find the length of \(\overline{G K}\), and then find the lengths of \(\overline{G J}\) and \(\overline{J K}\) to the nearest tenth of an inch.
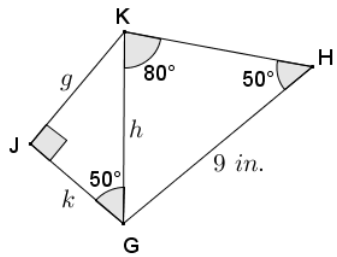
Answer:
By the angle sum of a triangle, m∠HGK = 50°; therefore,
∆ GHK is an isosceles triangle since its base ∠‘s have equal measure.
\(\frac{\sin 50}{h}=\frac{\sin 80}{9}\)
h = \(\frac{9 \sin 50}{\sin 80}\)
h ≈ 7.0
k = 7 cos 50 ≈ 4.5
g = 7 sin 50 ≈ 5.4
Question 5.
Given triangle LMN, LM = 10, LN = 15, and m∠L = 38°, use the law of cosines to find the length of \(\overline{M N}\) to the nearest tenth.
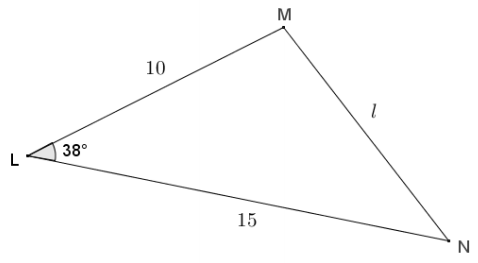
Answer:
l2 = 102 + 152 – 2(10)(15) cos 38
l2 = 100 + 225 – 300 cos 38
l2 = 325 – 300 cos 38
l2 = 325 – 300 cos 38
l = \(\sqrt{325-300 \cos 38}\)
l ≈ 9.4
MN = 9.4
The length of \(\overline{M N}\) is approximately 9.4 units.
Question 6.
Given triangle ABC, AC = 6, AB = 8, and m∠A = 78°, draw a diagram of triangle ABC, and use the law of cosines to find the length \(\overline{B C}\).
Answer:
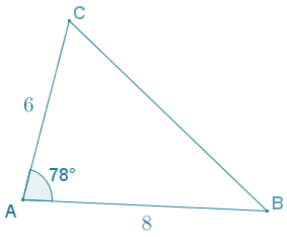
a2 = 62 + 82 – 2(6)(8)(cos 78)
a2 = 36 + 64 – 96(cos 78)
a2 = 100 – 96 cos 78
a = \(\sqrt{100-96 \cos 78}\)
a ≈ 8.9
The length of BC is approximately 8.9 units.
Calculate the area of triangle ABC.
Area = \(\frac{1}{2}\)bc(sin A)
Area = \(\frac{1}{2}\)(6)(8)(sin 78)
Area = 23. 5(sin 78)
Area ≈ 23.5
The area of triangle ABC is approximately 23.5 square units.
Eureka Math Geometry Module 2 Lesson 32 Exit Ticket Answer Key
Question 1.
Use the law of sines to find lengths b and c in the triangle below. Round answers to the nearest tenth as necessary.
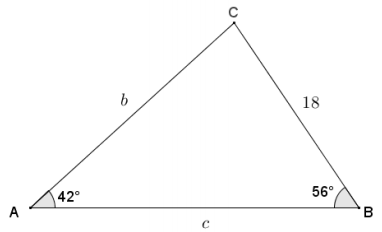
Answer:
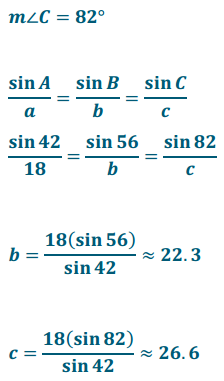
Question 2.
Given ∆ DEF, use the law of cosines to find the length of the side marked d to the nearest tenth.
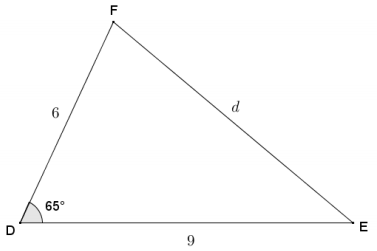
Answer:
d2 = 62 + 92 – 2(6)(9) (cos 65)
d2 = 36 + 81 – 108(cos 65)
d2 = 117 – 108 (cos 65)
d = \(\sqrt{117-108(\cos 65)}\)
d ≈ 8.4