Eureka Math Geometry Module 2 Lesson 31 Answer Key

Engage NY Eureka Math Geometry Module 2 Lesson 31 Answer Key

Eureka Math Geometry Module 2 Lesson 31 Example Answer Key

Example 1.
Find the area of ∆ GHI.
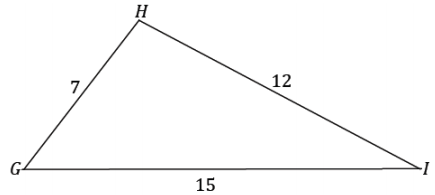
$Eureka Math Geometry Module 2 Lesson 31 Example Answer Key 1$
Answer:
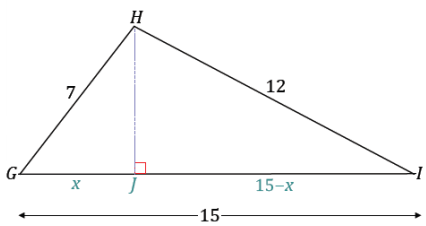
$Eureka Math Geometry Module 2 Lesson 31 Example Answer Key 2$

Allow students the opportunity and the time to determine what they must find (the height) and how to locate it (one option is to drop an altitude from vertex H to side $\overline{GI}$). For students who are struggling, consider showing just the altitude and allowing them to label the newly divided segment lengths and the height.

→ How can the height be calculated?
By applying the Pythagorean theorem to both of the created right triangles to find x,
h² = 49 – x² h² = 144 – (15 – x)²
49 – x² = 144 – (15 – x)²
49 – x² = 144- 225 + 30x – x²
130 = 30x
x = $\frac{13}{3}$
HJ = $\frac{13}{3}$, IJ = $\frac{32}{3}$

The value of x can then be substituted into either of the expressions equivalent to h² to find h.
h² = 49 – $\left(\frac{13}{3}\right)^{2}$
h² = 49 – $\frac{169}{9}$
h = $\frac{4 \sqrt{17}}{3}$

→ What is the area of the triangle?
Area = $\left(\frac{1}{2}\right)(15)\left(\frac{4 \sqrt{17}}{3}\right)$
Area = 10√17

Example 2.
A farmer is planning how to divide his land for planting next year’s crops. A triangular plot of land is left with two known
side lengths measuring 500 m and 1,700 m.
What could the farmer do next in order to find the area of the plot?
Answer:
→With just two side lengths known of the plot of land, what are the farmer’s options to determine the area of his plot of land?
He can either measure the third side length, apply the Pythagorean theorem to find the height of the triangle, and then calculate the area, or he can find the measure of the included angle between the known side lengths and use trigonometry to express the height of the triangle and then determine the area of the triangle.

→ Suppose the included angle measure between the known side lengths is 30°. What is the area of the plot of land? Sketch a diagram of the plot of land.
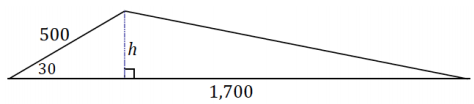
$Eureka Math Geometry Module 2 Lesson 31 Example Answer Key 3$
Area = $\frac{1}{2}$ (1700)(500) sin 30
Area = 212 500
The area of the plot of land is 212,500 square meters.

Eureka Math Geometry Module 2 Lesson 31 Opening Exercise Answer Key

Three triangles are presented below. Determine the areas for each triangle, if possible. If it is not possible to find the area with the provided information, describe what Is needed in order to determine the area.
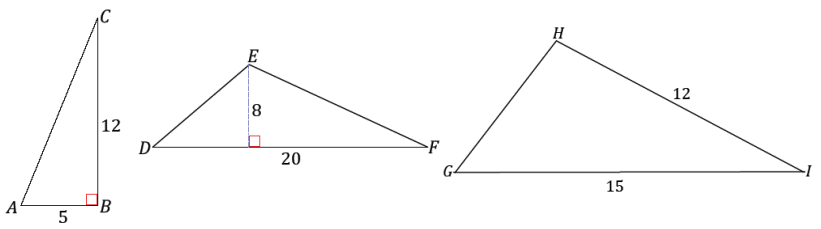
$Eureka Math Geometry Module 2 Lesson 31 Example Answer Key 4$
Answer:
The area of ∆ ABC is $\frac{1}{2}$(5)(12), or 30 square units, and the area of ∆ DEF is $\frac{1}{2}$ (8)(2o), or 80 square units. There is not enough information to find the height of ∆ GHI and, therefore, the area of the triangle.

Is there a way to find the missing information?
Answer:
Without further information, there is no way to calculate the area.

Eureka Math Geometry Module 2 Lesson 31 Exercise Answer Key

Exercise 1.
A real estate developer and her surveyor are searching for their next piece of land to build on. They each examine a plot of land in the shape of ∆ ABC. The real estate developer measures the length of $\overline{A B}$ and $\overline{A C}$ and finds them to both be approximately 4,000 feet, and the included angle has a measure of approximately 50°. The surveyor measures the length of $\overline{A C}$ and $\overline{B C}$ and finds the lengths to be approximately 4,000 feet and 3,400 feet, respectively, and measures the angle between the two sides to be approximately 65°.

a. Draw a diagram that models the situation, labeling all lengths and angle measures.
Answer:
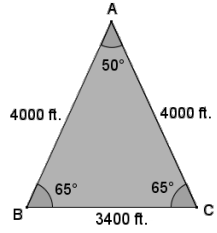
$Eureka Math Geometry Module 2 Lesson 31 Exercise Answer Key 5$

b. The real estate developer and surveyor each calculate the area of the plot of land and both find roughly the same area. Show how each person calculated the area; round to the nearest hundred. Redraw the diagram with only the relevant labels for both the real estate agent and surveyor.
Answer:
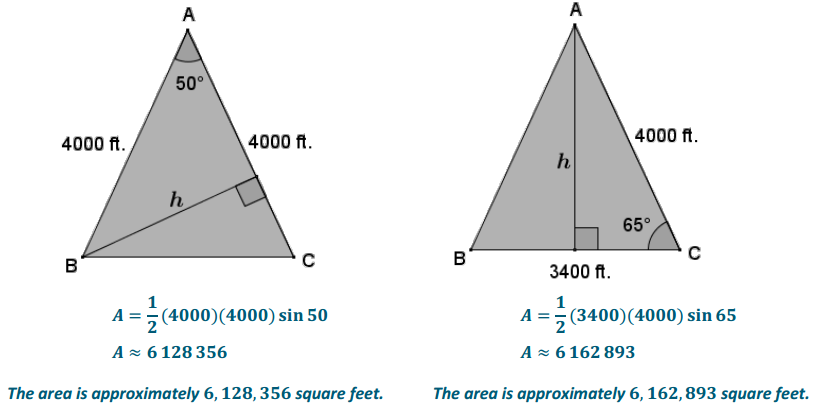
$Eureka Math Geometry Module 2 Lesson 31 Exercise Answer Key 6$

c. What could possibly explain the difference between the real estate agent’s and surveyor’s calculated areas?
Answer:
The difference in the area of measurements can be accounted for by the approximations of the measurements taken instead of exact measurements.

Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key

Find the area of each triangle. Round each answer to the nearest tenth.

Question 1.
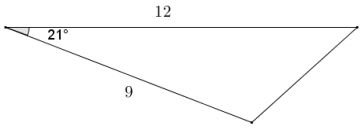
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 7$
Answer:
Area = $\frac{1}{2}$ (12)(9)(sin 21)
Area = 54(sin 21) ≈ 19.4
The area of the triangle is approximately 19.4 square units.

Question 2.
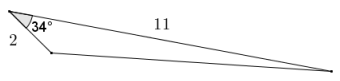
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 8$
Answer:
Area = $\frac{1}{2}$ (2)(11)(sin 34)
Area = 11(sin 34) ≈ 6.2
The area of the triangle is approximately 6.2 square units.

Question 3.
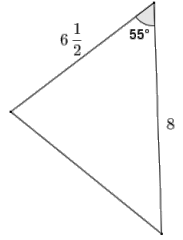
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 9$
Answer:
Area = $\frac{1}{2}$(8) (6$\frac{1}{2}$) (sin 55)
Area = 26(sin 55) ≈ 21.3
The area of the triangle is approximately 21.3 square units.

Question 4.
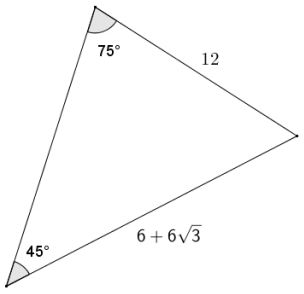
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 10$
Answer:
The included angle is 60° by the angle sum oía triangle.
Area = $\frac{1}{2}$ (12)(6 + 6√3) sin 60
Area = 6(6 + 6√3) $\left(\frac{\sqrt{3}}{2}\right)$
Area = (36 + 36√3) $\left(\frac{\sqrt{3}}{2}\right)$
Area = 18√3 + 18(3)
Area = 18√3 + 54 ≈ 85.2
The area of the triangle is approximately 85.2 square units.

Question 5.
In ∆ DEF, EF = 15, DF = 20, and m∠F = 63°. Determine the area of the triangle. Round to the nearest tenth.
Answer:
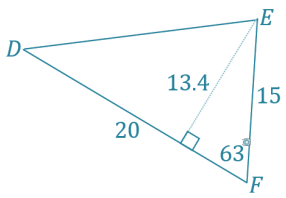
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 11$
Area = $\frac{1}{2}$ (20) (15) sin(63) ≈ 133.7
The area of ∆ DEF is 133.7 units².

Question 6.
A landscape designer is designing a flower garden for a triangular area that is bounded on two sides by the client’s house and driveway. The length of the edges of the garden along the house and driveway are 18 ft. and 8 ft., respectively, and the edges come together at an angle of 80°. Draw a diagram, and then find the area of the garden to the nearest square foot.
Answer:
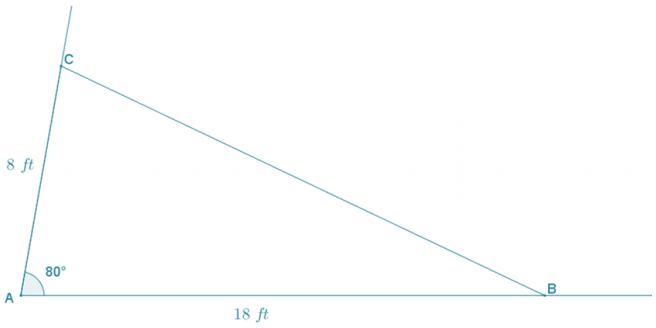
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 12$
The garden is in the shape of a triangle in which the lengths of two sides and the included angle have been provided.
Area(ABC) = $\frac{1}{2}$ (8 ft.)(18 ft.) sin 80
Area(ABC) = (72 sin 80) ft²
Area(ABC) ≈ 71 ft²

Question 7.
A right rectangular pyramid has a square base with sides of length 5. Each lateral face of the pyramid is an isosceles triangle. The angle on each lateral face between the base of the triangle and the adjacent edge is 75°. Find the surface area of the pyramid to the nearest tenth.
Answer:
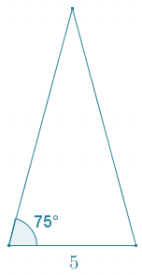
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 13$
Using tangent, the altitude of the triangle to the base of length 5 is equal to 2.5 tan 75.
Using tangent, the altitude of the triangle to the base of length 5 is equal to 2.5 tan 75.
Area = $\frac{1}{2}$ bh
Area = $\frac{1}{2}$ (5)(2.5 sin 75)
Area = 6. 25(sin 75)

The total surface area of the pyramid is the sum of the four lateral faces and the area of the square base:
SA = 4(6. 25(sin 75)) + 5²
SA = 25 sin 75 + 25
SA ≈ 49.1
The surface area of the right rectangular pyramid is approximately 49.1 square units.

Question 8.
The Pentagon building in Washington, DC, is built in the shape of a regular pentagon. Each side of the pentagon measures 921 ft. in length. The building has a pentagonal courtyard with the same center. Each wall of the center courtyard has a length of 356 ft. What is the approximate area of the roof of the Pentagon building?
Answer:
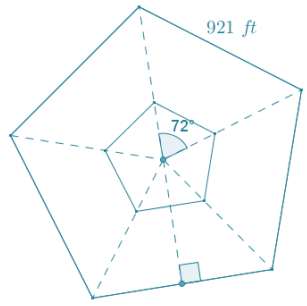
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 14$
Let A₁ represent the area within the outer perimeter of the Pentagon building in square feet.
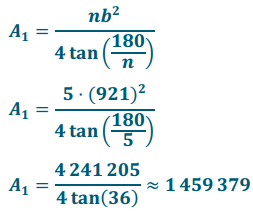
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 15$
The area within the outer perimeter of the Pentagon building is approximately 1,459, 379 ft².
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 16$
The area of the roof of the Pentagon building is approximately 1, 241, 333 ft².

Question 9.
A regular hexagon is inscribed in a circle with a radius of 7. Find the perimeter and area of the hexagon.
Answer:
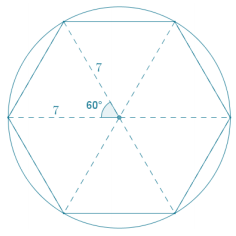
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 17$
The regular hexagon can be divided into six equilateral triangular regions with each side of the triangles having a length of 7. To find the perimeter of the hexagon, solve the following:
6 7 = 42, so the perimeter of the hexagon is 42 units.
To find the area of one equilateral triangle:
Area = $\frac{1}{2}$ (7)(7) sin 60
Area = $\frac{49}{2}\left(\frac{\sqrt{3}}{2}\right)$
Area = $\frac{49 \sqrt{3}}{4}$
The area of the hexagon is six times the area of the equilateral triangle.
Total Area = 6$\left(\frac{49 \sqrt{3}}{4}\right)$
Total Area = $\frac{147 \sqrt{3}}{2}$ ≈ 127.3
The total area of the regular hexagon is approximately 127.3 square units.

Question 10.
In the figure below, ∠AEB is acute. Show that Area (∆ ABC) = AC · BE · sin ∠AEB.
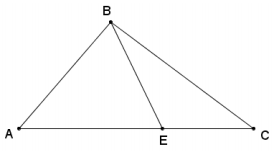
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 18$
Answer:
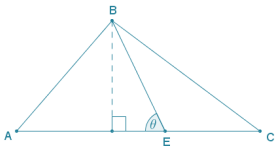
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 19$
Let θ represent the degree measure of angle AEB, and let h represent the altitude of ∆ ABC (and ∆ ABE).
Area(∆ ABC) = $\frac{1}{2}$ · AC · h
sin θ = $\frac{h}{B E}$ which implies that h = BE · sin θ.
Therefore, by substitution:
Area(∆ ABC) = $\frac{1}{2}$ AC · BE · sin ∠AEB.

Question 11.
Let ABCD be a quadrilateral. Let w be the measure of the acute angle formed by diagonals $\overline{AC}$ and $\overline{BD}$. Show that
Area(ABCD) = $\frac{1}{2}$ AC · BD · sin w.
(Hint: Apply the result from Problem 10 to ∆ ABC and ∆ ACD.)
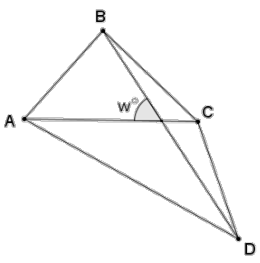
$Eureka Math Geometry Module 2 Lesson 31 Problem Set Answer Key 20$
Answer:
Let the intersection of $\overline{AC}$ and $\overline{BD}$ be called point P.
Using the results from Problem 10, solve the following:
Area(∆ ABC) = $\frac{1}{2}$AC · BP · sin w and
Area(∆ ADC) = $\frac{1}{2}$AC · PD · sin w
Area(ABCD) = ($\frac{1}{2}$AC · BP · sin w) + ($\frac{1}{2}$Ac · PD sin w) Area is additive.
Area(ABCD) = ($\frac{1}{2}$Ac. sin w) · (BP + PD) Distributive property
Area(ABCD) = ($\frac{1}{2}$Ac. sin w) · (BD) Distance is additive
And commutative addition gives us Area(ABCD) = $\frac{1}{2}$ · AC · BD · sin w.

Eureka Math Geometry Module 2 Lesson 31 Exit Ticket Answer Key

Question 1.
Given two sides of the triangle shown, having lengths of 3 and 7 and their included angle of 49°, find the area of the triangle to the nearest tenth.
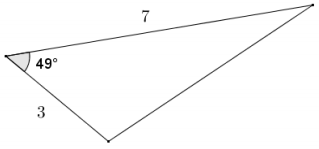
$Eureka Math Geometry Module 2 Lesson 31 Exit Ticket Answer Key 21$
Answer:
Area = $\frac{1}{2}$ (3)(7)(sin 49)
Area = 10. 5(sin 49) ≈ 7.9
The area of the triangle is approximately 7.9 square units.

Question 2.
In isosceles triangle PQR, the base QR = 11, and the base angles have measures of 71.45°. Find the area of ∆ PQR to the nearest tenth.
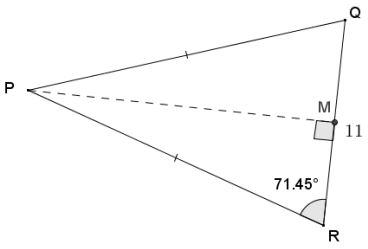
$Eureka Math Geometry Module 2 Lesson 31 Exit Ticket Answer Key 22$
Answer:
Drawing an altitude from P to midpoint M on $\overline{Q R}$ cuts the isosceles triangle into two right triangles with
QM = MR = 5.5. Using tangent, solve the following:
tan 71.45 = $\frac{P M}{5.5}$
PM = 5. 5(tan 71.45)
Area = $\frac{1}{2}$ bh
Area = $\frac{1}{2}$ (11)(5. 5(tan 71.45))
Area = 30. 25(tan 71.45) ≈ 90. 1
The area of the isosceles triangle is approximately 90.1 square units.