Engage NY Eureka Math Geometry Module 1 End of Module Assessment Answer Key
Eureka Math Geometry Module 1 End of Module Assessment Answer Key
Question 1.
Each of the illustrations on the next page shows in black a plane figure consisting of the letters F, R, E, and D evenly spaced and arranged in a row. In each illustration, an alteration of the black figure is shown in gray. In some of the illustrations, the gray figure is obtained from the black figure by a geometric transformation consisting of a single rotation. In others, this is not the case.

a. Which illustrations show a single rotation?
Answer:
Illustrations 2 and 5
b. Some of the illustrations are not rotations or even a sequence of rigid transformations. Select one such illustration, and use it to explain why it is not a sequence of rigid transformations.
Answer:
Illustrational 1 shows translations of individual letters F, R, E, and D; but each letter is translated a different distance. Since translation requires a shift of the entire plane by the same distance, illustrational does not qualify.
Question 2.
In the figure below, \(\overline{C D}\) bisects ∠ACB, AB = BC, m∠BEC = 90°, and m∠DCE = 42°. Find the measure of ∠A.
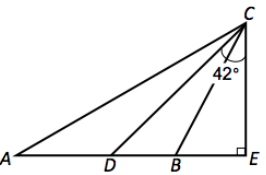
Answer:
Label the angles as shown.
(∠ACD ≅ ∠DCB since \(\overline{C D}\) bisects ∠ACB)
Since AB = BC, ∆ABC is isosceless, therefore 2x = a.
m∠A + m∠ACE + m∠E = 180°
a + (x + 42) + 90 = 180
2x + x + 132 = 180
x = 16
Since a = 2x, m∠A = 32°
Question 3.
In the figure below, \(\overline{A D}\) is the angle bisector of ∠BAC. \(\overline{B A P}\) and \(\overline{B D C}\) are straight lines, and \(\overline{A D}\) || \(\overline{P C}\). Prove that AP = AC.
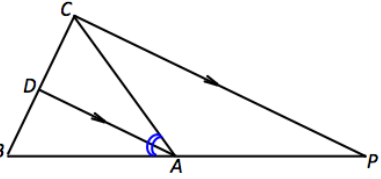
Answer:
Label w, x, y and z as shown.
| Statements | Reasons |
| 1. \(\overline{A D}\) is the angle bisector of ∠BAC | Given |
| 2. \(\overline{A D}\) || \(\overline{P C}\) | Given |
| 3. z = w | Definition of angle bisector |
| 4. z = y | If two parallel lines are cut by a transversal, alt. internal angles are equal in measure. |
| 5. w = x | If two parallel lines are cut by a tranversal, corr. Angles are equal in measure. |
| 6. x = y | Transitive property |
| 7. ∆ACP is isosceless | Base angles are congruent |
| 8. AC = AP | Definition of isosceles triangle. |
Question 4.
∆ ABC and ∆ DEF, in the figure below are such that \(\overline{A B}\) ≅ \(\overline{D E}\), \(\overline{A C}\) ≅ \(\overline{D F}\) and ∠A ≅∠D.
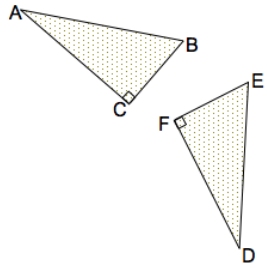
a. Which criteria for triangle congruence (ASA, SAS, SSS) implies that ∆ABC ≅ ∆DEF?
Answer:
side – Angle – side
b. Describe a sequence of rigid transformations that shows ∆ ABC ≅ ∆ DEF.
Answer:
- Translate ∆DEF so that F is mapped onto C.
- Rotate the image of ∆DEF about C so that E is mapped onto B.
- Reflect the image of the rotation across \(\overleftrightarrow{B C}\).
Question 5.
a. Construct a square ABCD with side \(\overline{A B}\). List the steps of the construction.

Answer:
- Extend \(\overline{A B}\) in both directions.
- Construct a perpendicular bisector to AB through a; Construct a perpendicular bisector to AB through B.
- Construct a circle with center A and radius AB; construct a circle with center B and raadius AB.
- Select a point where circle A meets the perpendicular through A and call that point D. on the same side of AB as D, select the point where circle B meets the perpendicular through B and call that point C.
- Draw segment CD.
b. Three rigid motions are to be performed on square ABCD. The first rigid motion is the reflection through \(\overline{B D}\). The second rigid motion is a 90° clockwise rotation around the center of the square.
Describe the third rigid motion that will ultimately map ABCD back to its original position. Label the image of each rigid motion A, B, C, and D in the blanks provided.
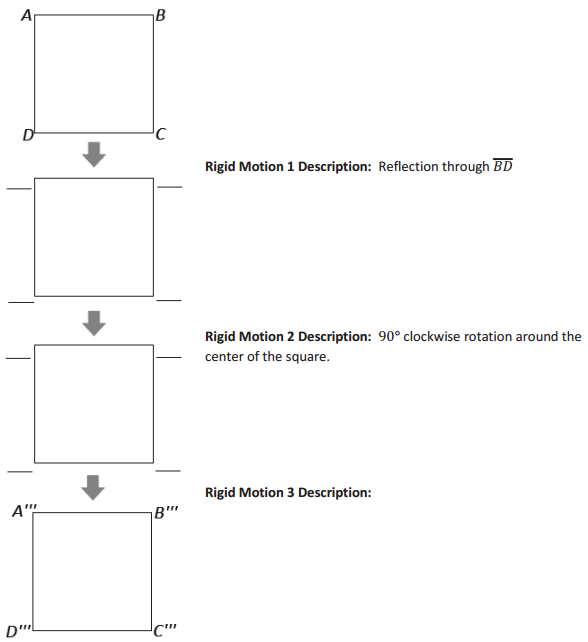
Answer:
Reflection through the line connecting the midpoint of AD and the midppoint of BC.
Question 6.
Suppose that ABCD is a parallelogram and that M and N are the midpoints of \(\overline{A B}\) and \(\overline{C D}\), respectively. Prove that AMCN is a parallelogram.
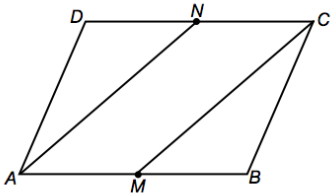
Answer:
| Statements | Reasons |
| 1. M and N are the mid points of \(\overline{A B}\) and \(\overline{C D}\) | Given |
| 2. ABCD is a parallelogram | Given |
| 3. AB = DC | Opposite sides of parallelogram are congruent |
| 4. NC = \(\frac{1}{2}\)DC | N is the mid point of DC |
| 5. AM = \(\frac{1}{2}\)AB | M is the mid point of AB |
| 6. AM = \(\frac{1}{2}\)DC | substitution |
| 7. AM = NC | Transitive property |
| 8. \(\overline{A B}\) || \(\overline{D C}\) | Definition of parallelogram |
| 9. \(\overline{A M}\) || \(\overline{N C}\) | M is on line AB, N is online DC |
| 10. AMCN is a parallelogram | Opposite sides are equal in length and parallel. |