Engage NY Eureka Math Geometry Module 1 Mid Module Assessment Answer Key
Eureka Math Geometry Module 1 Mid Module Assessment Answer Key
Question 1.
State precise definitions of angle, circle, perpendicular, parallel, and line segment based on the undefined notions of point, line, distance along a line, and distance around a circular arc.
Angle:
Circle:
Perpendicular:
Parallel:
Line segment:
Answer:
Angle:
An angle is formed by two rays that share a common vertex. An angle is proper if the two rays do not lie on the same line.
Circle:
A circle is the set of all points in a plane that are equidistant from the center point. The circle in plane P with center a and radius AB is the set of all points in P whose distance from A is the same as the distance from A to B.
Perpendicular:
Two lines are perpendicular if they have one point in common and if the four angles formed by the intersection are all right angles.
Parallel:
Two lines are parallel if they lie in the same plane and have no points in common.
Line segment:
A line segment is the set of point A and B and all points on line AB between A and B.
Question 2.
A rigid motion, J, of the plane takes a point, A, as input and gives C as output (i.e., J(A) = C). Similarly, J(B) = D for input point B and output point D.
Jerry claims that knowing nothing else about J, we can be sure that \(\overline{A C}\) ≅ \(\overline{B D}\) because rigid motions preserve distance.
a. Show that Jerry’s claim is incorrect by giving a counterexample (hint: a counterexample would be a specific rigid motion and four points A, B, C, and D in the plane such that the motion takes A to C and B to D, \(\overline{A C}\) ≅ \(\overline{B D}\) yet).
Answer:
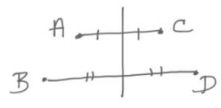
Here, J is a reflection across a vertical line. The distance from A to a line is different from the distance from B to the line. Therefore, the distance from A to its image (c) is different from the distance from B to its image(D).
b. There is a type of rigid motion for which Jerry’s claim is always true. Which type below is it?
A. Rotation
B. Reflection
C. Translation
Answer:
C. Translation
c. Suppose Jerry claimed that \(\overline{A B}\) ≅ \(\overline{C D}\). Would this be true for any rigid motion that satisfies the conditions described in the first paragraph? Why or why not?
Answer:
Yes, because rigid motions always preserve distance.
Question 3.
a. In the diagram below, l is a line, A is a point on the line, and B is a point not on the line. C is the midpoint of \(\overline{A B}\). Show how to create a line parallel to l that passes through B by using a rotation about C.
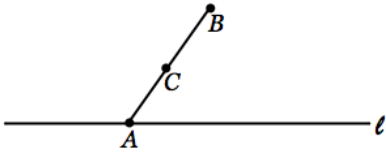
Answer:
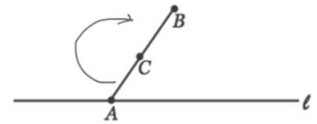
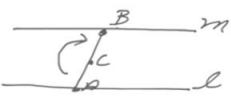
Take a 180° rotation about C. Line m is the image of l under this rotation. Line m passes through B and is parallel to l.
b. Suppose that four lines in a given plane, l1, l2, m1, and m2 are given, with the conditions (also given that l1 || l2, m1 || m2, and l1 is neither parallel nor perpendicular to m1.
i. Sketch (freehand) a diagram of l1, l2, m1, and m2 to illustrate the given conditions.
Answer:
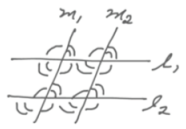
ii. In any diagram that illustrates the given conditions, how many distinct angles are formed? Count only angles that measure less than 1800, and count two angles as the same only if they have the same vertex and the same edges. Among these angles, how many different angle measures are formed? Justify your answer.
Answer:
There are distinct angles with two different angle measures because alternate interior/exterior angles are congruent and corresponding angles are congruent.
Question 4.
In the figure below, there is a reflection that transforms ∆ ABC to ∆\(A^{\prime} B^{\prime} C^{\prime}\). Use a straightedge and compass to construct the line of reflection, and list the steps of the construction.
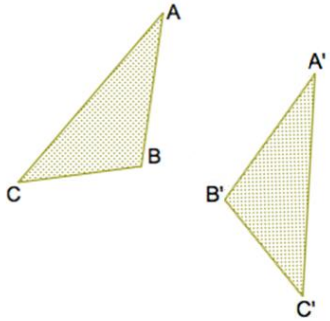
Answer:
1. Draw a segment B\(B^{\prime}\)
2. Construct circle B with radius
3. Construct circle \(B^{\prime}\) with radius
4. Connect the two intersections of circles B and \(B^{\prime}\)
5. This forms the line of reflection between ∆ABC and ∆\(A^{\prime}\)\(B^{\prime}\)\(C^{\prime}\)
Question 5.
Precisely define each of the three rigid motion transformations identified.
a. \(T_{\overrightarrow{A B}}(P)\)
Answer:
For vector \(\overrightarrow{A B}\), the translation along \(\overrightarrow{A B}\) is a translation of the plane:
(i) For every point P on line AB, \(T_{\overrightarrow{A B}}(P)\) is the point on \(\overrightarrow{A B}\) so that \(\overrightarrow{P Q}\) has the same length and direction as \(\overrightarrow{A B}\) and
(ii) For P not on \(\overrightarrow{A B}\), let l, be the line through P parallel to \(\overrightarrow{A B}\) and l2 be the line through B parallel to \(\overrightarrow{A B}\). Q is the intersection of l1 and l2.
b. rl(P)
Answer:
For a line l, a reflection across l is the transformation rl of the plane defined as follows:
(1) For any point p on line l, rl(P) = P, and
(2) For any point P no only rl(P) is the point Q so that l is the perpendicular bisector of \(\overrightarrow{P Q}\)
c. Rc, 30°(P)
Answer:
The rotation of 30° around center c is defined as follows:
(1) For the center C, Rc, 30°(C) = C, and
(2)For any other point P, Rc, 30° is the point Q that lies in the counterclockwise half-plane of ray \(\overrightarrow{C P}\) such that CQ = CP and ∠PCQ = 30°.
Question 6.
Given in the figure below, line lis the perpendicular bisector of \(\overline{A B}\) and of \(\overline{C D}\).
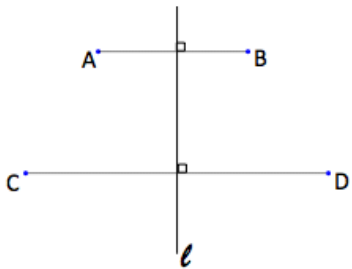
a. Show \(\overline{A C}\) ≅ \(\overline{B D}\)
Answer:
since l is the perpendicular bisector of \(\overline{A B}\) and \(\overline{C D}\), the reflection through line l brings A to B and C to D. Because reflections take line segments to congruent line segments \(\overline{A C}\) is the congruent to \(\overline{B D}\).
b. Show ∠ACD ≅ ∠BDC
Answer:
The reflection through line l brings A to B and C to D and D to C. Therefore ray \(\overrightarrow{C A}\) goes to ray \(\overrightarrow{D B}\), Ray \(\overrightarrow{C D}\) goes to ray \(\overrightarrow{D C}\). The image of ∠ACD is therefore congruent to ∠BDC.
c. Show \(\overline{A B}\) || \(\overline{C D}\).
Answer:
\(\overline{A B}\) || \(\overline{C D}\) because the perpendicular bisector intersects the two lines creating congruent corresponding angles.