Engage NY Eureka Math Algebra 2 Module 4 Lesson 1 Answer Key
Eureka Math Algebra 2 Module 4 Lesson 1 Exercise Answer Key
Exploratory Challenge/Exercises 1 – 13:
Exercise 1.
Would you change any of the assignments of 1 – 5 that Alan made? Explain your answer. Assign the numbers 1 – 5 to the event descriptions based on what you think is the best strategy to win the game.
| Outcome is an odd number on Spinner 1 and a red card from the card bag. | Outcome is an odd number on Spinner 1. |
Outcome is an odd number on Spinner 1 and a blue card from the card bag. | Outcome is an even number from Spinner 1 or a red card from the card bag. | Outcome is not a blue card from the card bag. |
Answer:
Answers will vary.
Exercise 2.
Carry out a turn by observing an outcome from spinning Spinner 1 and picking a card. How many points did you earn from this first turn?
Answer:
Answers will vary.
Exercise 3.
Complete four more turns (for a total of five), and determine your final score.
Player: Your Turn
Scoring Card for Scenario 1:
| Trial | Outcome from Spinner 1 | Outcome from the Card Bag | Points Based on Your Assignment of Numbers to the Events |
Answer:
Answers will vary depending on the outcomes when the student plays the game.
Exercise 4.
If you changed the numbers assigned to the descriptions, was your score better than Alan’s score? Did you expect your score to be better? Explain. If you did not change the numbers from those that Alan assigned, explain why you did not change them.
Answer:
Note: This question provides students on opportunity to begin explaining the strategy they ore using in this game. Anticipate that in most coses students are assigning the larger numbers (the 5 or the 4) to the outcomes they think are most likely.
At this point in the lesson, students have not been asked to calculate the actual probabilities of the events of interest. However, some students may have already calculated or estimated the probabilities. Anticipate that students change the assignment of numbers to try to improve their scores.
As students discuss strategies for assigning numbers based on whkh events are most likely to occur, they are also
evaluating the thinking of others.
Exercise 5.
Spinning Spinner 1 and drawing a card from the card bag is a chance experiment. One possible outcome of this experiment is (1, Blue-A). Recall that the sample space for a chance experiment is the set of all possible outcomes. What is the sample space for the chance experiment of Scenario Card 1?
Answer:
The sample space consists of 18 outcomes.
((1, Blue-A), (1, Blue-B), (1, Blue-C), (1, Blue-D), (1, Red-E), (1, Red-F), (2, Blue-A), (2, Blue-B), (2, Blue-C), (2, Blue-D), (2, Red-E), (2, Red-F), (3, Blue-A), (3, Blue-B), (3, Blue-C), (3, Blue-D), (3,Red-E), (3, Red-F)).
Exercise 6.
Are the outcomes in the sample space equally likely? Explain your answer.
Answer:
Yes, each outcome is equally likely to occur because the spinner is equally likely to land in any of the three segments, and each of the six cards is equally likely to be selected. The selection of a card and the result of spinning the spinner do not depend on each other, so the 18 outcomes in the sampk space should be equally likely.
Exercise 7.
Recall that an event is a collection of outcomes from the sample space. One event of interest for someone with Scenario Card 1 is “odd number on Spinner 1 and a red card.” What are the outcomes that make up this event? List the outcomes of this event in the first row of Table 1 (see Exercise 9).
Answer:
See the completed chart in Exercise 9.
Exercise 8.
What is the probability of getting an odd number on Spinner 1 and picking a red card from the card bag? Also enter this probability in Table 1 (see Exercise 9).
Answer:
See the completed table in Exercise 9. Direct students to write their probabilities as fractions or as decimals. Fractions do not need to be reduced, as the unreduced fractions are meaningful based on the context.
Exercise 9.
Complete Table 1 by listing the outcomes for the other events and their probabilities based on the chance experiment for this scenario card.
| Event | Outcomes | Probability |
| Odd number on Spinner 1 and a red card from the card bag |
||
| Odd number on Spinner 1 | ||
| Odd number on Spinner 1 and a blue card from the card bag |
||
| Even number on Spinner 1 or a red card from the card bag |
||
| Not picking a blue card from the card bag |
Answer:
The following table organizes the responses to Exercises 7 – 9:
| Event | Outcomes | Probability |
| Odd number on Spinner 1 and a red card from the card bag | Note: If students struggle with the “and” language, discuss the outcomes with students.
(, Red-E), (, Red-F), (, Red-E), |
The probability is, which is approximately .
Assign point to this event. |
| Odd number on Spinner 1
|
Note: Students may indicate that the probability of this outcome is the same as the probability of just getting an odd number on the spinner without considering the color of the card selected.
(, Blue-A), (, Blue-B), (, Blue-C), |
The probability is or, which is approximately.
Assign points to this event. |
| Odd number on Spinner 1 and a blue card from the card bag | (, Blue-A), (, Blue-B), (, Blue-C), (, Blue-D), (, Blue-A), (, Blue-B), (, Blue-C), (, Blue-D) |
The probability is, which is approximately.
Assign points to this event. |
| Even number on Spinner 1 or a red card from the card bag | Note: This event involves the “or.” Make sure students identify all of the outcomes that apply. This is an excellent event to discuss with students.
(, Red-E), (, Red-F), (, Blue-A), |
The probability is, which is approximately.
Assign points to this event. |
| Not picking a blue card from the card bag | Note: Although formally defined in Lesson 3, this is an example of the complement of the event “picking a blue card.” An informal discussion of the word “complement” may be considered; however, it is not necessary at this time.
(, Red-E), (, Red-F), (, Red-E), |
The probability is, which is approximately.
Assign points to this event. |
Exercise 10.
Based on the above probabilities, how would you assign the numbers 1 – 5 to each of the game descriptions? Explain.
Answer:
If players assigned the points based on a 5 assigned to the event most likely to occur, followed by 4, etc., then there would be changes made to the assignment of points.
Exercise 11.
If you changed any of the points assigned to the game descriptions, play the game again at least three times and record your final scores for each game. Do you think you have the best possible assignment of numbers to the events for this scenario card?
If you did not change the game descriptions, also play the game so that you have at least three final scores. Compare your scores with scores of other members of your class. Do you think you have the best assignment of numbers to the events for this scenario card?
| Turn | Outcome from Spinner 1 |
Outcome from the Card Bag |
Points Based on the Assignment of Points in Exercise 10 |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Answer:
Answers will vary. A good way to discuss this question with students is to compare the score Alan received with his assignment of points and the scores students received based on their assignments of points. Based on the assignment of points described in Exercise 10, one possible student response is shown below.
| Turn | Outcome from Spinner 1 |
Outcome from the Card Bag |
Points Based on the Assignment of Points in Exercise 10 |
| 1 | 2 | Blue | 4 |
| 2 | 1 | Red | 5 |
| 3 | 1 | Red | 5 |
| 4 | 3 | Blue | 5 |
| 5 | 2 | Blue | 4 |
The final score for the above five turns is 23 points. This is a better score than Alan received from his assignment of points.
Exercise 12.
Why might you not be able to answer the question of whether or not you have the best assignments of numbers to the game descriptions with at least three final scores?
Answer:
To decide the best assignment of points involves playing the game many times.
Note: Use this question to point out that probability is a long run relative frequency. For this example, to get a good sense of the probabilities, students would need to play the game many times.
Exercise 13.
Write your answers to the following questions independently, and then share your responses with a neighbor:
a. How did you make decisions about what to bet on?
Answer:
Answers will vary. I calculated the probability of each outcome and bet in the order of probability, 5 (greatest) to 1 (least). I used probability but changed a few bets based on the earlier outcomes.
b. How do the ideas of probability help you make decisions?
Answer:
Answers will vary. Calculating probability gives you a good idea of the number of times on outcome will occur and helps you make better decisions.
Eureka Math Algebra 2 Module 4 Lesson 1 Problem Set Answer Key
Consider a second scenario card that Alan created for his game:
Scenario Card 2
Tools: Spinner 1
Spinner 2: a spinner with six equal sectors (Place the number 1 in a sector, the number 2 in a second sector, the number 3 in a third sector, the number 4 in a fourth sector, the number 5 in a fifth sector, and the number 6 in the last sector.)
Directions (chance experiment): Spin Spinner 1, and spin Spinner 2. Record the number from Spinner 1, and record the number from Spinner 2.
Five Events of Interest:
|
Outcome is an odd number on |
Outcome is an odd number on Spinner 1 and an even number on Spinner 2. | Outcome is the sum of 7 from the numbers received from Spinner 1 and Spinner 2. |
Outcome is an even number on Spinner 2. |
Outcome is the sum of 2 from the numbers received from Spinner 1 and |
Player:
Scoring Card for Scenario 2:
| Turn | Outcome from Spinner 1 | Outcome for Spinner 2 | Points |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Question 1.
Prepare Spinner 1 and Spinner 2 for the chance experiment described on this second scenario card. (Recall that Spinner 2 has six equal sectors.)
Answer:
Prepare Spinner 2 as described. You can use the same Spinner 1 used for Scenario Card 1.
Question 2.
What is the sample space for the chance experiment described on this scenario card?
Answer:
There are 18 outcomes on this scenario card. Students can list all of the outcomes or describe them. Here is the list (the first number is the outcome from Spinner 1, and the second number is the outcome from Spinner 2);
(1, 1), (1,2), (1,3), (1,4), (1,5), (1,6), (2, 1), (2,2), (2,3), (2,4), (2.5), (2,6), (3, 1), (3,2), (3,3), (3,4), (3,5), (3,6)
Question 3.
Based on the sample space, determine the outcomes and the probabilities for each of the events on this scenario card. Complete the table below.
| Event | Outcomes | Probability |
| Outcome is an odd number on Spinner 2. |
||
| Outcome is an odd number on Spinner 1 and an even number on Spinner 2. |
||
| Outcome is the sum of 7 from the numbers received from Spinner 1 and Spinner 2. |
||
| Outcome is an even number on Spinner 2. |
||
| Outcome is the sum of 2 from the numbers received from Spinner 1 and Spinner 2. |
Answer:
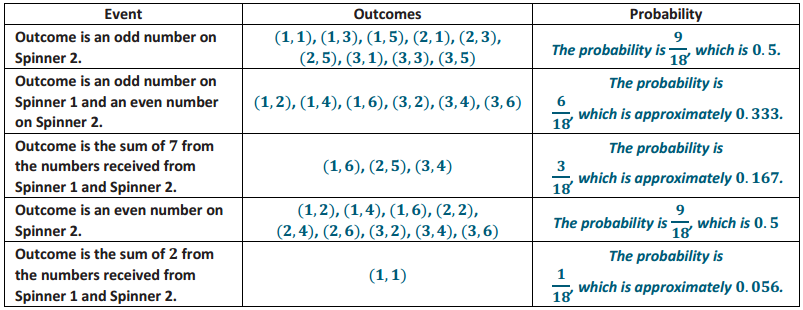
Note that although each event is different, some events are subsets of another event. As a result, students want to assign a larger number to the event with more outcomes. Expect that students obtain scores of 4 or 5 for each turn. As an extension, students may be asked to revise the descriptions of the events on the strategy cards in order to make the game more challenging.
Question 4.
Assign the numbers 1 – 5 to the events described on the scenario card.
Answer:
The following assignments would be based on the 5 assigned to the event with the greatest probability (the most likely outcome), to the event with the next largest, etc.:
Five Events of Interest: Scenario 2
| Outcome is an odd number on Spinner 2. |
Outcome is an odd number on Spinner 1 and an even number on Spinner 2. |
Outcome is the sum of 7 from the numbers received from Spinner 1 and Spinner 2. |
Outcome is an even number on Spinner 2. |
Outcome is the sum of 2 from the numbers received from Spinner 1 and Spinner 2. |
Answer:
| Outcome is an odd number on Spinner 2. |
Outcome is an odd number on Spinner 1 and an even number on Spinner 2. |
Outcome is the sum of 7 from the numbers received from Spinner 1 and Spinner 2. |
Outcome is an even number on Spinner 2. |
Outcome is the sum of 2 from the numbers received from Spinner 1 and Spinner 2. |
| 4 | 3 | 2 | 5 | 1 |
Question 5.
Determine at least three final scores based on the numbers you assigned to the events.
Player: Scott
| Trial | Outcome from Spinner 1 | Outcome for Spinner 2 | Points (see Problem 4) |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Player: Scott
| Trial | Outcome from Spinner 1 | Outcome for Spinner 2 | Points (see Problem 4) |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Player: Scott
| Trial | Outcome from Spinner 1 | Outcome for Spinner 2 |
Points (see Problem 4) |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 5 |
Answer:
Responses will vary. Provided are three final scores based on outcomes from carrying out the game.
Player Scott:
| Trial | Outcome from Spinner 1 | Outcome for Spinner 2 | Points (see Problem 4) |
| 1 | 2 | 6 | 5 |
| 2 | 1 | 5 | 4 |
| 3 | 2 | 6 | 5 |
| 4 | 3 | 3 | 4 |
| 5 | 2 | 2 | 5 |
Final Score: 23 Points
Player: Scott
| Trial | Outcome from Spinner 1 | Outcome for Spinner 2 | Points (see Problem 4) |
| 1 | 3 | 3 | 4 |
| 2 | 3 | 6 | 5 |
| 3 | 1 | 5 | 4 |
| 4 | 3 | 1 | 4 |
| 5 | 2 | 4 | 5 |
Final Score: 22 Points
Player: Scott
| Trial | Outcome from Spinner 1 | Outcome for Spinner 2 | Points (see Problem 4) |
| 1 | 2 | 2 | 5 |
| 2 | 1 | 1 | 4 |
| 3 | 1 | 4 | 5 |
| 4 | 3 | 3 | 4 |
| 5 | 2 | 2 | 5 |
Final Score: 23 Points
Question 6.
Alan also included a fair coin as one of the scenario tools. Develop a scenario card (Scenario Card 3) that uses the coin and one of the spinners, include a description of the chance experiment and descriptions of five events
relevant to the chance experiment.
Answer:
Answers will vary. Encourage students to be creative with this part of their assignment. Anticipate language similar to that used in the examples. A sample response card is included.
The following is an example of a completed Scenario Card 3:
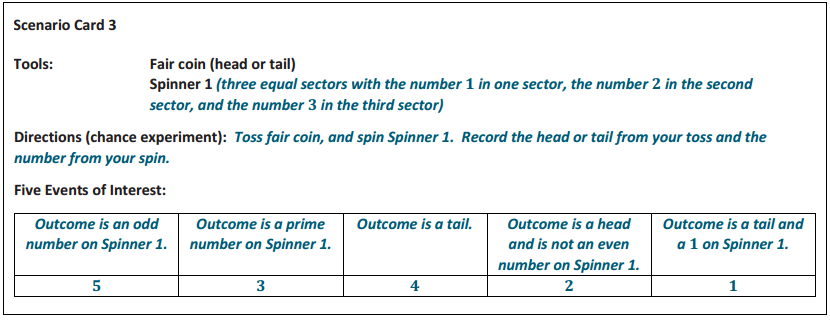
Question 7.
Determine the sample space for your chance experiment. Then, complete the table below for the five events on your scenario card. Assign the numbers 1 – 5 to the descriptions you created.
| Event | Outcomes |
Probability |
Answer:
Evaluate this chart based on the sample space and the descriptions developed by students. To evaluate, encourage
several students to explain their game scenario cards to other students, or provide a sample of the scenario cards
developed for students to try. The sample response is based on the scenario card presented in Problem 6.
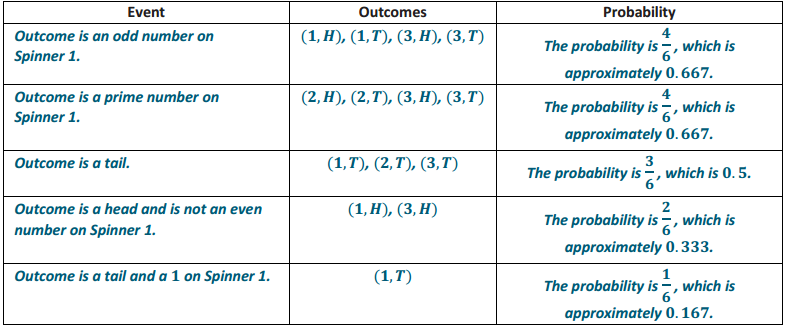
Question 8.
Determine a final score for your game based on five turns.
| Turn | Points | ||
Answer:
Answers vary based on the descriptions developed by students. Note: If time permits, encourage selected students to explain their games to other members of the class.
Eureka Math Algebra 2 Module 4 Lesson 1 Exit Ticket Answer Key
Question 1.
For the chance experiment described in Scenario Card 1, why is the probability of the event “spinning an odd number and randomly selecting a blue card” not the same as the probability of the event “spinning an even number and randomly selecting a blue card”? Which event would have the greater probability of occurring, and why?
Answer:
The first event includes the following outcomes from the sample space: (1, Blue-A), (1, Blue-B), (1, Blue-C), (1, Blue-D), (3, Blue-A), (3, Blue-B), (3, Blue-C), (3, Blue-D). The second event includes the following outcomes: (2, Blue-A), (2, Blue-B), (2, Blue-C), (2, Blue-D).
Because the spinner has two sectors representing odd numbers and only one sector representing an even number, the numbers of outcomes in the two events are different. The probability of the first event is \(\frac{8}{18}\) compared to the probability of \(\frac{4}{18}\) for the second event.
Question 2.
Why is the probability of the event “spinning an odd number from Spinner 1 and randomly selecting a blue card” not equal to the probability of “spinning an odd number from Spinner 1 or randomly selecting a blue card”?
Answer:
The outcomes for the first event must include both the odd number and a blue card or (1, Blue-A), (1, Blue-B), (1, Blue-C), (1, Blue-D), (3, Blue-A), (3,Blue-B), (3,Blue-C), and (3, Blue-D). The probability of that event would be \(\frac{8}{18}\) which is approximately 0.444. The outcomes of the second event would include each of the above outcomes, but it would also include the outcomes of odd numbers from the spinner with a red card and even numbers with a blue card.
The outcomes for this event include (1, Blue-A), (1, Blue-B), (1, Blue-C), (1, Blue-D), (1, Red-E), (1, Red-F), (2, Blue-A), (2,Blue-B), (2, Blue-C), (2, Blue-D), (3,Blue-A), (3,Blue-B), (3,Blue-C), (3, Blue-D), (3, Red-E), and (3, Red-F) . The only outcomes not included would be red cards with an even number. The probability for this event is \(\frac{16}{18^{\prime}}\) which is approximately 0.889.
Question 3.
If one of the red cards is changed to a blue card, what is the probability of the event “spinning an odd number from Spinner 1 and randomly selecting a red card from the card bag”?
Answer:
Changing one red card to a blue card will result in five blue cards and one red card in the card bag. Each of the five blue cards could be paired with each odd number that is possible from the spinner (the number 1 or the number 3). There would be a total of ten outcomes for this event. The number of outcomes in the sample space, however, would not change. As a result, the probability of this event is \(\frac{10}{18^{\prime}}\) which is approximately 0.556.