Engage NY Eureka Math Algebra 2 Module 4 Lesson 4 Answer Key
Eureka Math Algebra 2 Module 4 Lesson 4 Example Answer Key
Exercise 1:
In previous lessons, conditional probabilities were used to investigate whether or not there is a connection between two events. This lesson formalizes this idea and introduces the concept of independence.
1.
Several questions are posed below. Each question is about a possible connection between two events. For each question, identify the two events, and indicate whether or not you think that there would be a connection. Explain your reasoning.
a. Are high school students whose parents or guardians set a midnight curfew less likely to have a traffic violation
than students whose parents or guardians have not set such a curfew?
Answer:
Responses vary.
The two events are parents set a midnight curfew and students have o traffic violation. Anticipate that students may indicate either that students with a curfew are less likely to have a traffic violation or that there is no connection. Either answer is acceptable as long as students provide an explanation.
b. Are left-handed people more likely than right-handed people to be interested in the arts?
Answer:
Responses vary.
The two events are people are right-handed and people are interested in the arts. Students may argue that there is a connection or that there is nota connection between being right-handed and being interested in the arts. Look for some reasoning that indicates that if one of the descriptions is met (selecting a right- handed person), it is more (or less) likely this person is also interested in the arts. Students may indicate that they do not think that there is a connection, which is acceptable as long as they explain their reasoning.
c. Are students who regularly listen to classical music more likely to be interested in mathematics than students who do not regularly listen to classical music?
Answer:
Responses vary.
The two events are “students regularly listen to classical music†and “students are interested in mathematics. Students may argue that there is a connection or there is not a connection between classical music and an interest in mathematics. Look for some reasoning that indicates that the fane of the descriptions is met, it is more likely the other description will or will not occur.
d. Are people who play video games more than 10 hours per week more likely to select football as their favorite sport than people who do not play video games more than 10 hours per week?
Answer:
Responses vary.
The two events are people who play video games more than 10 hours per week and people whose favorite sport is football. Students may argue that there is a connection or there is not a connection between video games and an interest in football, which is acceptable as long as they explain their reasoning.
Two events are independent when knowing that one event has occurred does not change the likelihood that the second event has occurred. How can conditional probabilities be used to tell if two events are independent or not independent?
Exercises 2 – 6:
Recall the hypothetical 1000 two-way frequency table that was used to classify students at Rufus King High School according to gender and whether or not they participated in an after-school athletics program.
Table 1: Participation of Male and Female Students in an After-School Athletics Program
| Participate in an After-School Athletics Program | Do Not Participate in an After-School Athletics Program |
Total | |
| Female | |||
| Male | |||
| Total |
Answer:
| Participate in an After-School Athletics Program | Do Not Participate in an After-School Athletics Program |
Total | |
| Female | 232 | 348 | 580 |
| Male | 168 | 252 | 420 |
| Total | 400 | 600 | 1,000 |
Exercise 2.
For each of the following, indicate whether the probability described is one that can be calculated using the values in Table 1. Also indicate whether or not it is a conditional probability.
a. The probability that a randomly selected student participates in an after-school athletics program
Answer:
This probability can be calculated from the values in the table. It is not a conditional probability. The probability is based on the entire school population.
b. The probability that a randomly selected student who is female participates in an after-school athletics program
Answer:
This probability can be calculated from the values in the table. it is a conditional probability because it is a probability-based on only the female students at the school.
c. The probability that a randomly selected student who is male participates in an after-school athletics program
Answer:
This probability can be calculated from the values in the table. It is a conditional probability because it is based on only the male students at the school.
Exercise 3.
Use Table 1 to calculate each of the probabilities described in Exercise 2.
a. The probability that a randomly selected student participates in an after-school athletics program
Answer:
\(\frac{400}{1000}\) = 0. 400 (This means that 40% of all students participate in after-school athletics programs.)
b. The probability that a randomly selected student who is female participates in an after-school athletics
program
Answer:
\(\frac{232}{580}\) = 0.400 (This means that 40% of female students participate in after-school athletics programs.)
c. The probability that a randomly selected student who is male participates in an after-school athletics program
Answer:
\(\frac{168}{420}\) = 0.400 (This means that 40% of male students participate in after-school athletics programs.)
Exercise 4.
Would your prediction of whether or not a student participates in an after-school athletics program change if you knew the gender of the student? Explain your answer.
Answer:
No. Based on the conditional probabilities, the probability that o student participates in an after-school athletics program is 0.400 for both male and female students.
Two events are independent if knowing that one event has occurred does not change the probability that the other event has occurred. For example, consider the following two events:
F: The event that a randomly selected student is female
S: The event that a randomly selected student participates in an after-school athletics program.
Events F and S would be independent if the probability that a randomly selected student participates in an after-school athletics program is equal to the probability that a randomly selected student who is female participates in an after-school athletics program.
If this was the case, knowing that a randomly selected student female does not change the probability that the selected student participates in an after-school athletics program. Then, F and S would be independent.
Exercise 5.
Based on the definition of independence, are the events randomly selected student is female and randomly selected student participates in an after-school athletics program independent? Explain.
Answer:
Yes, they are independent because knowing that a randomly selected student is female does not change the probability that the selected student participates in an after-school athletics program. The probability that a randomly selected student participates in an after-school athletics program is 0.400, and the probability that a randomly selected student who is female participates is also 0.400.
Exercise 6.
A randomly selected student participates in an after-school athletics program.
a. What is the probability this student is female?
Answer:
\(\frac{232}{400}\) = 0.58
This is equal to the probability that a randomly selected student is female.
b. Using only your answer from part (a), what is the probability that this student is male? Explain how you arrived at your answer.
Answer:
The probability is 0.42.
The probability in part (a) can be interpreted as 58% of the students who participate in after-school athletics programs are female. The rest must be male, so the probability that a randomly selected student who participates in an after-school athletics program is male is 0.42. 1 – 0.58 = 0.42
Exercises 7 – 11:
Consider the data below.
| No Household Member Smokes | At Least One Household Member Smokes | Total | |
| Student Has Asthma | 69 | 113 | 182 |
| Student Does Not Have Asthma | 473 | 282 | 755 |
| Total | 542 | 395 | 937 |
Exercise 7.
You are asked to determine if the two events a randomly selected student has asthma and a randomly selected student has a household member who smokes are independent. What probabilities could you calculate to answer this question?
Answer:
Students could indicate that the probability of selecting a student who has a household member who smokes is the same for students who have asthma as for those who do not have asthma. Or students could indicate that the probability of selecting a student who has a household member who smokes from the students who have asthma would need to be equal to the probability of selecting a student who has a household member who smokes from all of the students.
Or students could Indicate that the probability of selecting a student who has a household member who smokes from the students who do not have asthma would need to be equal to the probability of selecting a student who has a household member who smokes from all of the students.
Students could also indicate that conditional probabilities based on the columns would have to be equal for the events to be independent. The probability of selecting a student who has asthma from the students who have no household member who smokes would need to be equal to the probability of selecting a student who has asthma from the students who have at least one household member who smokes.
Exercise 8.
Calculate the probabilities you described in Exercise 7.
Answer:
The row conditional probabilities described are as follows:
\(\frac{69}{182}\) = 0.379
\(\frac{473}{755}\) = 0.626
The column conditional probabilities described ore as follows:
\(\frac{69}{542}\) = 0.127
\(\frac{113}{395}\) = 0.286
Exercise 9.
Based on the probabilities you calculated in Exercise 8, are these two events independent or not independent? Explain.
Answer:
No. The conditional probabilities need to be equal for the events to be independent.
Exercise 10.
Is the probability that a randomly selected student who has asthma and who has a household member who smokes the same as or different from the probability that a randomly selected student who does not have asthma but does have a household member who smokes? Explain your answer.
Answer:
The probabilities are different as the events are not independent. The probability of a randomly selected student
who has asthma having a household member who smokes is \(\frac{113}{182^{\prime}}\) which is approximately 0.62. The probability of a randomly selected student who does not have asthma having a household member who smokes is \(\frac{282}{755^{\prime}}\) which is approximately 0.37.
Exercise 11.
A student is selected at random. The selected student indicates that he has a household member who smokes. What is the probability that the selected student has asthma?
Answer:
\(\frac{113}{395}\) = 0.29 This is the conditional probability that a randomly selected student who has a household family member who smokes has asthma.
Eureka Math Algebra 2 Module 4 Lesson 4 Problem Set Answer Key
Question 1.
Consider the following questions:
a. A survey of the students at a Midwest high school asked the following questions:
Do you use a computer at least 3 times a week to complete your schoolwork?
Are you taking a mathematics class?
Do you think the events “a randomly selected student uses a computer at least 3 times a week” and “a randomly selected student is taking a mathematics class†are independent or not independent? Explain your reasoning.
Answer:
Anticipate students indicate that using a computer at least 3 times per week and taking a mathematics class are not independent. However, it is also acceptable for students to make a case for independence. Examine the explanations students provide to see if they understand the meaning of independence.
b. The same survey also asked students the following:
“Do you participate in any extracurricular activities at your school?”
“Do you know what you want to do after high school?”
Do you think the events “a randomly selected student participates in extracurricular activities” and “a randomly selected student knows what she wants to do after completing high school” are independent or not, independent? Explain your reasoning.
Answer:
Answers will vary. Anticipate students indicate that students involved in extracurricular activities are often students who want to attend college. It is likely the events are not independent.
c. People attending a professional football game in 2013 completed a survey that included the following questions:
“Is this the first time you have attended a professional football game?”
“Do you think football is too violent?”
Do you think the events “a randomly selected person who completed the survey Is attending a professional football game for the first time” and “a randomly selected person who completed the survey thinks football is too violent” are independent or not independent? Explain your reasoning.
Answer:
Answers will vary. Anticipate that students indicate that people who attend football more often are more likely to not think the game is too violent it is likely the events are not independent. Again, examine the explanations students provide if they indicate the events are not independent.
Question 2.
Complete the table below in a way that would indicate the two events “uses a computer” and “is taking a mathematics class” are independent.
| Uses a Computer at Least Times a Week for Schoolwork | Does Not Use a Computer at Least Times a Week for Schoolwork | Total | |
| In a Mathematics Class | 700 | ||
| Not in a Mathematics Class | |||
| Total | 600 | 1,000 |
Answer:
| Uses a Computer at Least Times a Week for Schoolwork | Does Not Use a Computer at Least Times a Week for Schoolwork | Total | |
| In a Mathematics Class | 420 | 280 | 700 |
| Not in a Mathematics Class | 180 | 120 | 300 |
| Total | 600 | 400 | 1,000 |
Question 3.
Complete the following hypothetical 1000 table. Are the events “participates in extracurricular activities” and “know what I want to do after high school” independent or not independent? Justify your answer.
| Participates in Extracurricular Activities | Does Not Participate in Extracurricular Activities | Total | |
| Know What I Want to Do After High School | 800 | ||
| Do Not Know What I Want to Do After High School | 50 | ||
| Total | 600 | 1,000 |
Answer:
| Participates in Extracurricular Activities | Does Not Participate in Extracurricular Activities | Total | |
| Know What I Want to Do After High School | 550 | 250 | 800 |
| Do Not Know What I Want to Do After High School | 50 | 150 | 200 |
| Total | 600 | 400 | 1,000 |
The events “student participates in extracurricular activities” and “student knows what I want to do after high school are not independent. Students could indicate that the events are not independent in several ways.
For example, \(\frac{50}{200}\) (the probability that a randomly selected student who does not know what he wants to do after high school participates in extracurricular activities) does not equal \(\frac{550}{800}\) (the probability that a randomly selected student who does know what he wants to do after high school participates in extracurricular activities).
Question 4.
The following hypothetical 1000 table is from lesson 2.
| No Household Member Smokes | At Least One Household Member Smokes | Total | |
| Student Has Asthma | 73 | 120 | 193 |
| Student Does Not Have Asthma | 506 | 301 | 807 |
| Total | 579 | 421 | 1,000 |
The actual data from the entire population are given in the table below.
| No Household Member Smokes | At Least One Household Member Smokes | Total | |
| Student Has Asthma | 69 | 113 | 182 |
| Student Does Not Have Asthma | 473 | 282 | 755 |
| Total | 542 | 395 | 937 |
a. Based on the hypothetical 1000 table, what is the probability that a randomly selected student who has asthma has at least one household member who smokes?
Answer:
\(\frac{120}{193}\) = 0.622
b. Based on the actual data, what is the probability that a randomly selected student who has asthma has at least one household member who smokes (round your answer to 3 decimal places)?
Answer:
\(\frac{113}{182}\) = 0.621
c. Based on the hypothetical 1000 table, what is the probability that a randomly selected student who has no household member who smokes has asthma?
Answer:
\(\frac{73}{579}\) = 0.126
d. Based on the actual data, what is the probability that a randomly selected student who has no household member who smokes has asthma?
Answer:
\(\frac{69}{542}\) = 0.127
e. What do you notice about the probabilities calculated from the actual data and the probabilities calculated
from the hypothetical 1000 table?
Answer:
The conditional probabilities differ only due to rounding in constructing the hypothetical 1000 table from probability information based on the actual data. When an actual data table is available, it can be used to calculate probabilities.
When only probability information is available, constructing a hypothetical 1000 table from that information and using it to compute other probabilities will give some answers as if the actual data were available.
Question 5.
As part of the asthma research, the investigators wondered if students who have asthma are less likely to have a pet at home than students who do not have asthma. They asked the following two questions:
“Do you have asthma?”
“Do you have a pet at homer?”
Based on the responses to these questions, you would like to set up a two-way table that you could use to determine if the following two events are independent or not independent:
Event 1: A randomly selected student has asthma.
Event 2: A randomly selected student has a pet at home.
a. How would you label the rows of the two-way table?
Answer:
Anticipate students indicate for the rows “Has Asthma” and “Does Not Have Asthma.” Students might use these labels for the columns rather thon the rows, which is also acceptable.
b. How would you label the columns of the two-way table?
Answer:
Anticipate students indicate for the columns “Has a Pet” and “Does Not Have a Pet.”
c. What probabilities would you calculate to determine if Event 1 and Event 2 are independent?
Answer:
Answers may vary. Row conditional probabilities or column conditional probabilities would have to be equal if the events are independent. For column conditional probabilities (based on the definition of rows and columns above), this would mean that the probability that a randomly selected student who has a pet has asthma is equal to the probability that a randomly selected student who does not have a pet has asthma.
Eureka Math Algebra 2 Module 4 Lesson 4 Exit Ticket Answer Key
Question 1.
The following hypothetical 1000 two-way table was introduced in the previous lesson:
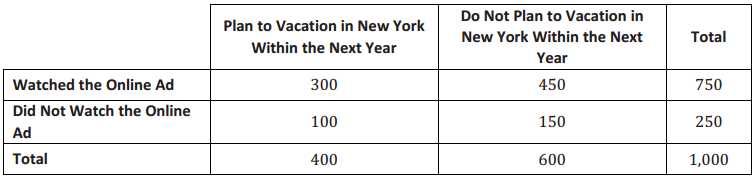
Are the events “a randomly selected person watched the online ad” and “a randomly selected person plans to vacation in New York within the next year’ independent or not independent? Justify your answer using probabilities calculated from the information in the table.
Answer:

The conditional probabilities that could be used to evaluate if the events are independent are the probability that given the selected member watched the online ad, the member plans to vacation in New York, and the probability that given the selected member did not watch the ad, the member plans to vacation in New York. Because the probabilities are equal, the events are independent.
\(\frac{300}{750}\) = 0.40 and \(\frac{100}{250}\) = 0.40
Question 2.
A survey conducted at a local high school indicated that 30% of students have a job during the school year. If having a job and being in the eleventh grade are not independent, what do you know about the probability that a randomly selected student who is in the eleventh grade would have a job? Justify your answer.
Answer:
The probability that a student selected from the eleventh grade has a job would not be equal to 0.30. Not independent means that knowing the selected student is in the eleventh grade changes the probability that the student has a job.
Question 3.
Eighty percent of the dogs at a local kennel are in good health. If the events “a randomly selected dog at this kennel is in good health” and “a randomly selected dog at this kennel weighs more than 30 pounds” are independent, what do you know about the probability that a randomly selected dog that weighs more than 30 pounds will be in good health? Justify your answer.
Answer:
As the events are independent, knowing that the selected dog weighs more than 30 pounds does not change the probability that the dog is in good health. This means that the probability that a large dog is in good health is also 0.80.