Engage NY Eureka Math Algebra 2 Module 3 Lesson 9 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 9 Opening Exercise Answer Key
Opening Exercise:
a. Evaluate WhatPower2(8). State your answer as a logarithm, and evaluate It.
Answer:
log2(8) = 3
b. Evaluate WhatPower5(625). State your answer as a logarithm, and evaluate it.
Answer:
log5(625) = 4
Eureka Math Algebra 2 Module 3 Lesson 9 Exploratory Challenge Answer Key
Exploratory Challenge:
Autumn is starting a new club with eight members including herself. She wants everyone to have a secret identification code made up of only A’s and B’s, known as an ID code. For example, using two characters, her ID code could be AA.
a. Using A’s and B’s, can Autumn assign each club member a unique two-character ID code using only A’s and B’s? Justify your answer. Here’s what Autumn has so far.
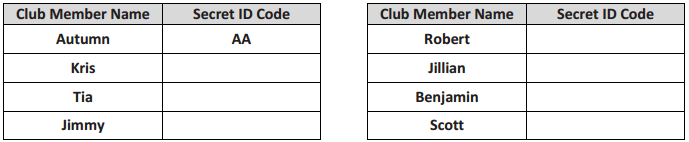
Answer:
No, she cannot assign a unique 2-character ID code to each member. The only codes available are AA, BA, AB, and BB, and there are eight people.
b. Using A’s and B’s, how many characters would be needed to assign each club member a unique ID code? Justify your answer by showing the ID codes you would assign to each club member by completing the table above (adjust Autumn’s ID if needed).
Answer:
You would need three characters in each ID code. A completed table is shown below. Students could assign one of the unique codes to any club member, so this is not the only possible solution.
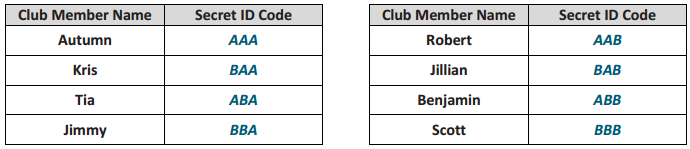
When the club grew to 16 members, Autumn started noticing a pattern.
Using A’s and B’s:
i. Two people could be given a secret ID code with 1 letter: A and B.
ii. Four people could be given a secret ID code with 2 letters: AA, BA, AB, BB.
iii. Eight people could be given a secret ID code with 3 letters: AAA, BAA, ABA, BBA, AAB, BAB, ABB, BBB.
c. Complete the following statement, and list the secret ID codes for the 16 people. 16 people could be given a secret ID code with _________ letters using A’s and B’s.
Answer:
16 people could be given a secret ID code with 4 characters. Notice the original members have their original three-character code with an A added to the end. Then, the newer members have the original three-character codes with a B added to the end.
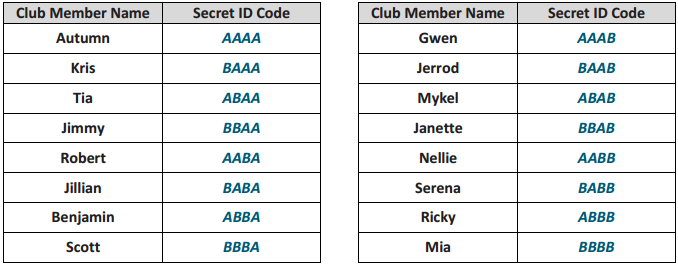
d. Describe the pattern in words. What type of function could be used to model this pattern?
Answer:
The number of people in the club is a power of 2. The number of characters needed to generate a unique ID code using only two characters is the exponent of the power of 2.
log2(2) = 1
log2(4) = 2
log2(8) = 3
log2(16) = 4
A logarithm function could be used to model this pattern. For 16 people, you will need a four-character ID code because log2(16) = 4.
Eureka Math Algebra 2 Module 3 Lesson 9 Exercise Answer Key
Exercises 1 – 2:
In the previous problems, the letters A and B were like the digits In a number. A four-digit ID code for Autumn’s club could be any four-letter arrangement of A’s and B’s because, in her ID system, the only digits are the letters A and B.
Exercise 1.
When Autumn’s club grows to include more than 16 people, she will need five digits to assign a unique ID code to each club member. What is the maximum number of people that could be in the club before she needs to switch to a six-digit ID code? Explain your reasoning.
Answer:
Since log2(32) = 5 and log2(64) = 6, she will need to switch to a six-digit ID code when the club grows to more than 32 members.
Exercise 2.
If Autumn has 256 members in her club, how many digits would she need to assign each club member a unique ID code using only A’s and B’s? Show how you got your answers.
Answer:
She will need 8 digits because log2(256) = 8.
Example:
A thousand people are given unique identifiers made up of the digits 0, 1, 2, …, 9. How many digits would be needed for each ID number?
Answer:
You would just need three digits: (000, 001, 002, …, 099, 100, 101, …, 998, 999).
Exercises 3 – 4:
Exercise 3.
There are approximately 317 million people in the United States. Compute and use log(100000000) and log(l000000000) to explain why Social Security numbers are 9 digits long.
Answer:
We know that log(100000000) = 8, which is the number of digits needed to assign an ID number to loo million people. We know that log(l000000000) = 9, which is the number of digits needed to assign an ID number to 1 billion people. The United States government will not need to increase the number of digits in a Social Security number until the United States population reaches one billion.
Exercise 4.
There are many more telephones than the number of people in the United States because of people having home phones, cell phones, business phones, fax numbers, etc. Assuming we need at most 10 billion phone numbers in the United States, how many digits would be needed so that each phone number is unique? Is this reasonable? Explain.
Answer:
Since log( 10000000000) = 10, you would need a ten-digit phone number in order to have ten billion unique numbers. Phone numbers in the United States are 10 digits long. If you divide 10 billion by 317 million (the number of people in the United States), that would allow for approximately 31 phone numbers per person. That is plenty of numbers for individuals to have more than one number, leaving many additional numbers for businesses and the government.
Eureka Math Algebra 2 Module 3 Lesson 9 Problem Set Answer Key
Question 1.
The student body president needs to assign each officially sanctioned club on campus a unique ID code for purposes of tracking expenses and activities. She decides to use the letters A, B, and C to create a unique three-character code for each club.
a. How many clubs can be assigned a unique ID code according to this proposal?
Answer:
Since log3(27) = 3, the president could assign codes to 27 clubs according to this proposal.
b. There are actually over 500 clubs on campus. Assuming the student body president still wants to use the letters A, B, and C, how many characters would be needed to generate a unique ID code for each club?
Answer:
We need to estimate log3(500). Since 35 = 243 and 36 = 729, she could use a six-character combination of letters and have enough unique IDs for up to 729 clubs.
Question 2.
Can you use the numbers 1, 2, 3, and 4 in a combination of four digits to assign a unique ID code to each of 500 people? Explain your reasoning.
Answer:
log4(4) = 1
log4(16) = 2
log4(64) = 3
log4(256) =4
log4(1024) = 5
No. You would need to use a five-digit ID code using combinations of 1’s, 2’s, 3’s, and 4’s such as 11111 or 12341, or you could use the numbers 1 to 5 in four characters such as 1231, 1232, 1233, 1234, 1235, etc., because
log5(625) = 4.
Question 3.
Automobile license plates typically have a combination of letters (26) and numbers (10). Over time, the state of New York has used different criteria to assign vehicle license plate numbers.
a. From 1973 to 1986, the state used a 3-letter and 4-number code where the three letters indicated the county where the vehicle was registered. Essex County had 13 different 3-letter codes in use. How many cars could be registered to this county?
Answer:
Since log(10000) = 4, the 4-digit code could be used to register up to 10,000 vehicles. Multiply that by 13 different county codes, and up to 130,000 vehicles could be registered in Essex County.
b. Since 2001, the state has used a 3-letter and 4-number code but no longer assigns letters by county. Is this coding scheme enough to register 10 million vehicles?
Answer:
Since log26(x) = 3 when x = 263 = 17,576, there are 17,576 three-letter codes. Since log(l0000) = 4, there are 10,000 four-digit codes. Multiply 17576 . 10,000 = 175,760,000, and we see that this scheme generates over 100 million license plate numbers.
Question 4.
The Richter scale uses base 10 logarithms to assign a magnitude to an earthquake based on the amount of force released at the earthquake’s source as measured by seismographs in various locations.
a. Explain the difference between an earthquake that is assigned a magnitude of 5 versus one assigned a magnitude of 7.
Answer:
The difference between S and 7 is 2, so a magnitude of 7 would be 102, or 100, times greater force.
b. An earthquake with magnitude 2 can usually only be felt by people located near the earthquake’s origin, called its epicenter. The strongest earthquake on record occurred in Chile In 1960 with magnitude 9. 5. How many times stronger is the force of an earthquake with magnitude 9. 5 than the force of an earthquake with magnitude 2?
Answer:
The difference between 2 and 9. 5 is 7.5, so it would be about 107.5 times the force. This is approximately 31 million times greater force.
c. What is the magnitude of an earthquake whose force is 1,000 times greater than a magnitude 4.3 quake?
Answer:
Since 103 = 1000, the magnitude would be the sum of 4.3 and 3, which is 7.3.
Question 5.
Sound pressure level is measured in decibels (dB) according to the formula L = 10 log (\(\frac{I}{I_{0}}\)), where I is the intensity of the sound and I0 is a reference intensity that corresponds to a barely perceptible sound.
a. Explain why this formula would assign 0 decibels to a barely perceptible sound.
Answer:
If we let I = I0, then
L = 10 log(\(\frac{I}{I_{0}}\))
L = 10 log(1)
L = 10 . 0
L = 0.
Therefore, the reference intensity is always 0 dB.
b. Decibel levels above 120 dB can be painful to humans. What would be the intensity that corresponds to this level?
Answer:
120 = 10 log (\(\frac{I}{I_{0}}\))
1.2 = log(\(\frac{I}{I_{0}}\))
\(\frac{I}{I_{0}}\) = 101.2
I ≈ 15.8I0
From this equation, we can see that the intensity is about 16 times greater than barely perceptible sound.
Eureka Math Algebra 2 Module 3 Lesson 9 Exit Ticket Answer Key
Question 1.
A brand-new school district needs to generate ID numbers for its student body. The district anticipates a total enrollment of 75, 000 students within the next ten years. Will a five-digit ID number using the symbols 0, 1, …, 9 be enough? Explain your reasoning.
Answer:
log(10000) = 4 and log(100000) = 5, so 5 digits should be enough. However, students who enter school at the kindergarten level in the tenth year of this numbering scheme would need to keep their IDs for 13 years. Dividing 75,000 by 13 shows there would be roughly 6,000 students per grade.
Adding that many students per year would take the number of needed IDs at any one time over 100,000 in just a few more years. The district should probably use a six-digit ID number.