Engage NY Eureka Math Algebra 2 Module 3 Lesson 10 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 10 Opening Exercise Answer Key
Opening Exercise:
Find the value of the following expressions without using a calculator.
WhatPower10(1000) =
Answer:
3
log10(1000) = Answer:
3
WhatPower10(100) =
Answer:
2
log10(100) =
Answer:
2
WhatPower10(10) =
Answer:
1
log10(10) =
Answer:
1
WhatPower10(1) =
Answer:
0
log10(1) =
Answer:
0
WhatPower10(\(\frac{1}{10}\)) =
Answer:
-1
log10(\(\frac{1}{10}\)) =
Answer:
-1
WhatPower10(\(\frac{1}{100}\)) =
Answer:
-2
log10(\(\frac{1}{100}\)) =
Answer:
-2
Formulate a rule based on your results above: If k is an integer, then log10(10k) = ______
Answer:
1og10(10k) = k
Eureka Math Algebra 2 Module 3 Lesson 10 Example Answer Key
Example 1:
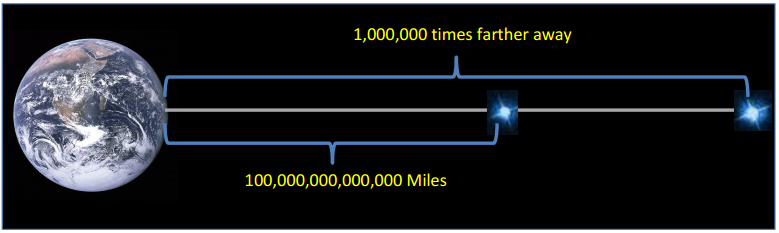
(100,000,000,000,000) (1,000,000) = 100,000,000,000,000,000,000, so the second star is 100 quintillion miles away from Earth.
→ How did you arrive at that figure?
I counted the zeros; there are 14 zeros in 100,000,000,000,000 and 6 zeros in 1,000,000, so there must be 20 zeros in the product.
→ Can we restate that in terms of exponents?
(1014) (106) = 1020
→ How are the exponents related?
14 + 6 = 20
→ What are log(1014), log(106), and log(1020)?
14, 6, and 20
→ In this case, can we state an equivalent expression for log(1014 . 106)?
log(1014 . 106) = log(1014) + log(106)
→ Why is this equation true?
log(1014 106) = log(1020) = 20 = 14 + 6 = log(1014) + log(106)
→ Generalize to find an equivalent expression for log(lOm . 109 for integers m and n. Why is this equation true?
log(10m . 10n) = log(10m + n) = m + n = log(10m) + log(10n)
This equation is true because when we multiply powers of 10 together, the resulting product is a power of 10 whose exponent is the sum of the exponents of the factors.
→ Keep this result in mind as we progress through the lesson.
Eureka Math Algebra 2 Module 3 Lesson 10 Exercise Answer Key
Exercises:
Exercise 1.
Find two consecutive powers of 10 so that 30 is between them. That is, find an integer exponent k so that
10k < 30 < 10k + 1
Answer:
Since 10 < 30 < 100, we have k = 1.
Exercise 2.
From your result in Exercise 1, log(30) is between which two integers?
Answer:
Since 30 is some power of 10 between 1 and 2, 1 < log(30) < 2.
Exercise 3.
Find a number k to one decimal place so that 10k < 30 < 10k + 0.1, and use that to find under and overestimates for log(30).
Answer:
Since 101.4 ≈ 25.1189 and 101.5 ≈ 31.6228, we have 101.4 < 30 < 101.5. Then 1.4 < log(30) < 1.5, and k ≈ 1.4.
Exercise 4.
Find a number k to two decimal places so that 10k < 30 < 10k + 0.01, and use that to find under and overestimates for log(30).
Answer:
Since 101.47 ≈ 29.5121, and 101.48 ≈ 30.1995, we have 101.47 < 30 < 101.48 so that 1.47 < log(30) < 1.48. So, k ≈ 1.47.
Exercise 5.
Repeat this process to approximate the value of log(30) to 4 decimal places.
Answer:
Since 101.477 ≈ 29.9916, and 101.478 ≈ 30.0608, we have 101.477 < 30 < 101.478 so that 1.477 < log(30) < 1.478.
Since 101.4771 ≈ 29.9985, and 101.4772 ≈ 30.0054, we have 101.4771 < 30 < 101.4772 so that 1.4771 < log(30) < 1.4772.
Since 101.47712 ≈ 29.9999, and 101.47713 ≈ 30.0006, we have 101.47712 < 30 < 1.47713 so that 1.47712 < log(30) < 1.47713.
Thus, to four decimal places, log(30) ≈ 1.4771.
Exercise 6.
Verify your result on your calculator, using the LOG button.
Answer:
The calculator gives log(30) ≈ 1.477121255.
Exercise 7.
Use your calculator to complete the following table. Round the logarithms to 4 decimal places.
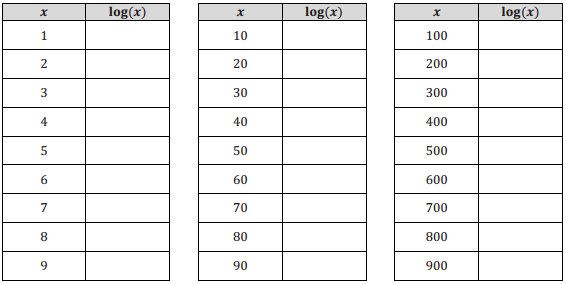
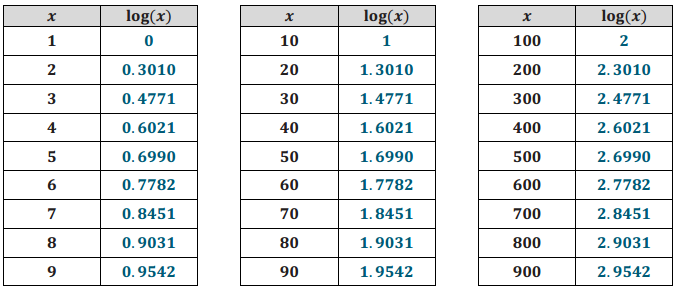
Answer:
Exercise 8.
What pattern(s) can you see in the table from Exercise 7 as x is multiplied by 10? Write the pattern(s) using logarithmic notation.
Answer:
I found the patterns log(10x) = 1 + log(x) and log(100x) = 2 + log(x). I also noticed that log(100x) = 1 + log(10x).
Exercise 9.
What pattern would you expect to find for log(l000x)? Make a conjecture, and test it to see whether or not it appears to be valid.
Answer:
I would guess that the values of log(1000x) will all start with 3. That is, log(1000x) = 3 + log(x). This appears to be the case since log(2000) ≈ 3.3010, log(5000) ≈ 3.6990, and log(8000) ≈ 3.9031.
Exercise 10.
Use your results from Exercises 8 and 9 to make a conjecture about the value of log(10” x) for any positive integer k.
Answer:
It appears that log(10k . x) = k + log(x), for any positive integer k.
Exercise 11.
Use your calculator to complete the following table. Round the logarithms to 4 decimal places.
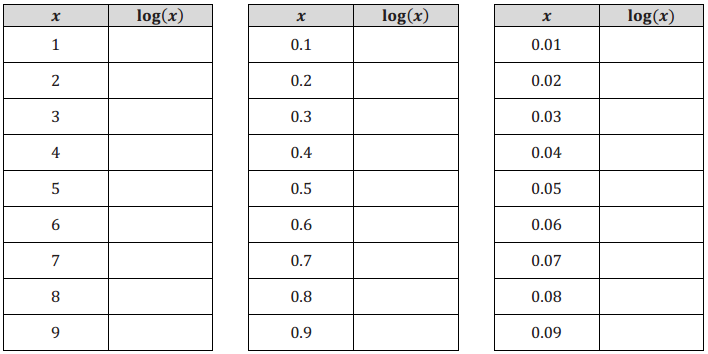
Answer:
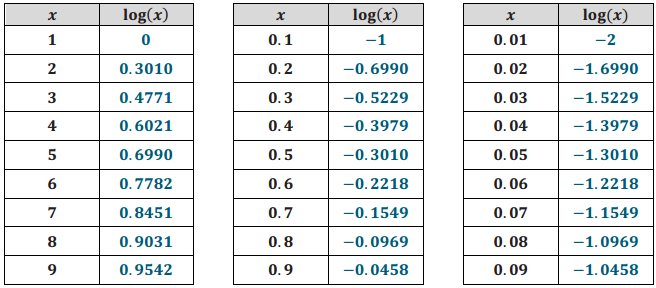
Exercise 12.
What pattern(s) can you see In the table from Exercise 11? Write them using logarithmic notation.
Answer:
I found the patterns log(x) – log (\(\frac{x}{10}\)) = 1, which can be written as log (\(\frac{x}{10}\)) = -1 + log(x), and log (\(\frac{x}{100}\)) = -2 + log(x).
Exercise 13.
What pattern would you expect to find for log (\(\frac{x}{1000}\))? Make a conjecture, and test it to see whether or not It appears to be valid.
Answer:
I would guess that the values of log(\(\frac{x}{1000}\)) will all start with -2 and that log (\(\frac{x}{1000}\)) = -3 + log(x). This appears to be the case since log(0.002) ≈ -2.6990, and -2.6990 = -3 + 0.3010; log(0.005) ≈ -2.3010, and -2.3010 = -3 + 0.6990; log(0.008) ≈ -2.0969, and -2.0969 = -3 + 0.9031.
Exercise 14.
Combine your results from Exercises 10 and 12 to make a conjecture about the value of the logarithm for a multiple of a power of 10; that is, find a formula for log(10k . x) for any integer k.
Answer:
It appears that log(10k . x) = k + log(x), for any integer k.
Eureka Math Algebra 2 Module 3 Lesson 10 Problem Set Answer Key
Question 1.
Complete the following table of logarithms without using a calculator; then, answer the questions that follow.
Answer:
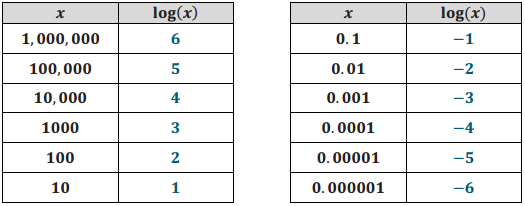
a. What is log(1)? How does that follow from the definition of a base-10 logarithm?
Answer:
Since 100 = 1, we know that log(1) = 0.
b. What is log(10k) for an integer k? How does that follow from the definition of a base-10 logarithm?
Answer:
By the definition of the logarithm, we know that log(10k) = k.
c. What happens to the value of log(x) as x gets really large?
Answer:
For any x> 1, there exists k > 0 so that 10k < x < 10k + 1 As x gets really large, k gets large. Since k ≤ log(x) < k + 1, as k gets large, log(x) gets large. d. For x > 0, what happens to the value of log(x) as x gets really close to zero?
Answer:
For any 0 < x < 1, there exists k > 0 so that 10-k < x < 10k + 1. Then -k ≤ x < -k + 1. As x gets closer to zero, k gets larger. Thus, log(x) is negative, and |log(x)| gets large as the positive number x gets close to zero.
Question 2.
Use the table of logarithms below to estimate the values of the logarithms in parts (a) – (h).
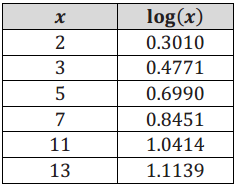
a. log(70000)
Answer:
4.8451
b. log(O. 0011)
Answer:
-2.9586
c. log(20)
Answer:
1.3010
d. log(0.00005)
Answer:
-4.3010
e. log(130 000)
Answer:
5.1139
f. log(3000)
Answer:
3.4771
g. log(0.07)
Answer:
-1.1549
h. log(11000000)
Answer:
7.0414
Question 3.
If log(n) = 0.6, find the value of log(10n).
Answer:
log(10n) = 1.6
Question 4.
If m is a positive integer and log(m) ≈ 3.8, how many digits are there in m? Explain how you know.
Answer:
Since 3 < log(m) < 4, we know 1,000 < m < 10,000; therefore, m has 4 digits.
Question 5.
If m is a positive integer and log(m) ≈ 9. 6, how many digits are there in m? Explain how you know.
Answer:
Since 9 < log(m) < 10, we know 109 < m < 1010; therefore, m has 10 digits.
Question 6.
Vivian says log(452000) = 5 + log(4.52), while her sister Lillian says that log(452000) = 6 + log(0.452). Which sister is correct? Explain how you know.
Answer:
Both sisters are correct. Since 452,000 = 4.52 . 105, we can write log(452000) = 5 + log(4.52). However, we could also write 452,000 = 0.452 . 106, so log(452000) = 6 + log(0.452). Both calculations give log(452,000) ≈ 5.65514.
Question 7.
Write the base-10 logarithm of each number in the form k + log(x), where k is the exponent from the scientific notation, and x is a positive real number.
a. 24902 × 104
Answer:
4+ log(2.4902)
b. 2.58 × 1013
Answer:
13+ log(2.58)
c. 9.109 × 1o-31
Answer:
-31 + log(9.109)
Question 8.
For each of the following statements, write the number in scientific notation, and then write the logarithm base 10 of that number in the form k + log(x), where k is the exponent from the scientific notation, and x is a positive real number.
a. The speed of sound is 1116ft/s.
Answer:
1116 = 1.116 × 103, so log(1116) = 3 + log(1.116).
b. The distance from Earth to the sun is 93 million miles.
Answer:
93,000,000 = 9.3 × 107, so log(93000000) = 7 + log(9.3).
c. The speed of light is 29,980,000,000 cm/s.
Answer:
29,980,000,000 = 2.998 × 1010, so log(29, 980,000, 000) = 10 + log(2.998).
d. The weight of Earth is 5,972, 000,000,000, 000,000,000, 000 kg.
Answer:
5, 972, 000, 000, 000, 000, 000, 000, 000 = 5.972 × 1024, so
log(5,972,000,000,000, 000,000,000,000) = 24 + log(5.972).
e. The diameter of the nucleus of a hydrogen atom is 0. 00000000000000175 m.
Answer:
0.00000000000000175 = 1.75 × 10-15, so log(0. 00000000000000175) = -15 + log(1.75).
f. For each part (a) – (e), you have written each logarithm in the form k + log(x), for integers k and positive real numbers x. Use a calculator to find the values of the expressions log(x). Why are all of these values between 0 and 1?
Answer:
log(1.116) ≈ 0.047664
log(9.3) ≈ 0.968483
log(2.998) ≈ 0.476832
log(5.972) ≈ 0.77612
log(1.75) ≈ 0.243038
These values are all between 0 and 1 because x is between 1 and 10. We can rewrite 1 < x < 10 as 100 < x < 101. If we write x = 10L for some exponent L, then 100 < 10L < 101, so 0 < L < 1. This exponent L is the base 10 logarithm of X.
Eureka Math Algebra 2 Module 3 Lesson 10 Exit Ticket Answer Key
Question 1.
Use the logarithm table below to approximate the specified logarithms to four decimal places. Do not use a calculator.
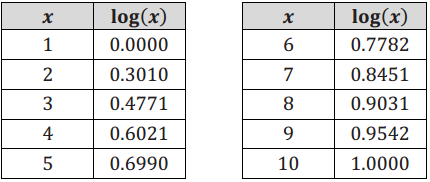
a. log( 500)
Answer:
log(500) = log(102 . 5)
= 2 + log(5)
≈ 2.6990
b. log(0.0005)
Answer:
log(0.0005) = log(10-4 . 5)
= -4 + log(5)
≈ -3.3010
Question 2.
Suppose that A is a number with log(A) = 1.352.
a. What is the value of log(1000A)?
Answer:
log(1000A) = log(103A) = 3 + log(A) = 4.352
b. Which one of the following statements is true? Explain how you know.
i. A < 0
ii. 0 < A < 10
iii. 10 < A < 100
iv. 100 < A < 1000 v. A >1000
Answer:
Because log(A) = 1.352 = 1 + 0.352, A is greater than 10 and less than 100. Thus, (iii) is true. In fact, from the table above, we can see that A is between 20 and 30 because of log(20) ≈ 1.3010, and log(30) ≈ 1. 4771.