Engage NY Eureka Math Algebra 2 Module 3 Lesson 32 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 32 Mathematical Modeling Exercise Answer Key
Mathematical Modeling Exercise:
Now that you have studied the mathematics of structured savings plans, buying a car, and paying down a credit card debt, it’s time to think about the mathematics behind the purchase of a house. In the problem set in Lesson 31, you selected a future career and a home to purchase. The question of the day is this: Can you buy the house you have chosen on the salary of the career you have chosen? You need to adhere to the following constraints:
→ Mortgages are loans that are usually offered with 30-, 20-, or 15- year repayment options. Start with a 30-year mortgage.
→ The annual interest rate for the mortgage will be 5%.
→ Your payment includes the payment of the loan for the house and payments into an account called an escrow account, which is used to pay for taxes and insurance on your home. We approximate the annual payment to escrow as 1.2% of the home’s selling price.
→ The bank can only approve a mortgage if the total monthly payment for the house, including the payment to the escrow account, does not exceed 30% of your monthly salary.
→ You have saved up enough money to put a 10% down payment on this house.
Exercise 1.
Will the bank approve a 30-year mortgage on the house that you have chosen?
Answer:
I chose the career oía graphic designer, with a starting salary of $39, 900. My monthly salary is
\(\frac{\$ 39900}{12}\) = $3325
Thirty percent of my $3,325 monthly salary is $997. 50.
I found a home that is suitable for $190.000.
Since 0.012(190000) = 2280, I need to contribute $2,280 to escrow for the year, which means I need to pay $190 to escrow each month.
I will make a $19,000 down payment, meaning that I need a mortgage for $171,000.
APPROACH 1:
We can think of the total owed on the house in two different ways.
→ If we had placed the original loan amount = 171000 in a savings account earning 5% annual interest, then the future amount in 30 years would be Af = Ap(1 + i)360
→ If we deposit a payment of R into an account monthly and let the money in the account accumulate and earn interest for 30 years, then the future value is
Af = R + R(1 + i) + R(1 + i)2 + …. + R(1+i)359
= R\(\sum_{k=0}^{359}\)(1 + i)k
= R\(\left(\frac{1-(1+i)^{360}}{1-(1+i)}\right)\)
= R\(\left(\frac{(1+i)^{360}-1}{i}\right)\)
Setting these two expresions for Af equal to each other, we have
Ap(1 + i)360 = R\(\left(\frac{(1+i)^{360}-1}{i}\right)\)
R = \(\frac{A_{p} \cdot i \cdot(1+i)^{360}}{(1+i)^{360}-1}\),
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-360}}\)
This is the formula for the present value of an annuity, but rewritten to isolate R.
Then using my values of Ap, i and n we have
R = \(\frac{171000(0.004167)}{1-(1.004167)^{-360}}\)
R = 918.01.
Then, the monthly payment on the house I chose would be R + 190 = 1 108.01. The bank will not lend me the money to buy this house because $1, 108.01 is higher than $997.50.
APPROACH 2:
From Lesson 30, we know that the present value of an annuity formula is A = R\(\left(\frac{1-(1+i)^{-n}}{i}\right)\), where i is the monthly interest rate, R is the monthly payment, and n is the number of months in the term. In my example, i = \(\frac{0.05}{12}\) ≈ 0.004167, R is unknown, n = 12.30 = 360, and Ap = 171000. We can solve the above formula for R, then we can substitute the known values of the variables and calculate the resulting payment R.
Ap = R\(\left(\frac{1-(1+i)^{-n}}{i}\right)\)
Ap . i = R(1 – (1 + i)-n)
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
Then using my values of Ap, i and n we have
R = \(\frac{171000(0.004167)}{1-(1.004167)^{-360}}\)
R = 918.01.
Then, the monthly payment on the house ichose would be R + 190 = 1108.01. The bank will not lend me the money to buy this house because $1, 108.01 is higher than $997.50.
Exercise 2.
Answer either (a) or (b) as appropriate.
a. If the bank approves a 30-year mortgage, do you meet the criteria for a 20-year mortgage? If you could get a mortgage for any number of years that you want, what is the shortest term for which you would qualify?
Answer:
(This scenario did not happen in this example.)
b. If the bank does not approve a 30-year mortgage, what is the maximum price of a house that fits your budget?
Answer:
The maximum that the bank allows for my monthly payment is 30% of my monthly salary, which is $997. 50. This includes the payment to the loan and to escrow. If the total price of the house is H dollars, then I will make a down payment of 0.1H and finance 0.9H. Using the present value of an annuity formula, we have
0.9H = R\(\left(\frac{1-(1+i)^{-n}}{i}\right)\)
0.9H = R \(\left(\frac{1-(1.004167)^{-360}}{0.004167}\right)\)
0. 9H = R(186.282)
However, R represents just the payment to the loan and not the payment to the escrow account. We know that the escrow portion is one-twelfth of 1.2% of the house value. If we denote the total amount paid for the loan and escrow by P, then P = R + 0.001H, so R = P – 0.001H. We know that the largest value for P is P = 997.50, so then
0.9H = R(186.282)
0.9H = (997.50 – 0.001H)(186.282)
0.9H = 185816 – 0. 186282H
1.086282H = 185816
H = 171056.87
Then, I can only afford a house that is priced at or below $171,056.87.
Eureka Math Algebra 2 Module 3 Lesson 32 Problem Set Answer Key
Question 1.
Use the house you selected to purchase in the Problem Set from Lesson 31 for this problem.
a. What was the selling price of this house?
Answer:
Student responses will vary. The sample response will continue to use a house that sold for $190,000.
b. Calculate the total monthly payment, R, for a 15-year mortgage at 5% annual interest, paying 10% as a down payment and an annual escrow payment that is 1.2% of the full price of the house.
Answer:
Using the payment formula with Ap = 0.9(190000) = 171000, i = \(\frac{0.05}{12}\) ≈ 0.004167, and n = 15 . 12 = 180, we have
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(171000)(0.004167)}{1-(1.004167)^{-180}}\)
≈ 1352.29
The escrow payment is \(\frac{1}{12}\)(0.012)($190000) = $190.00. The total monthly payment is
$1,352.29 + $190.00 = $1, 542.29.
Question 2.
In the summer of 2014, the average listing price for homes for sale in the Hollywood Hills was $2,663,995.
a. Suppose you want to buy a home at that price with a 30-year mortgage at 5. 25% annual interest, paying 10% as a down payment and with an annual escrow payment that is 1.2% of the full price of the home. What is your total monthly payment on this house?
Answer:
Using the payment formula with Ap = 0.9(2663995) = 2397595.50, i = \(\frac{0.0525}{12}\) ≈ 0.004375, and n = 360, we have
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(2397595.50)(0.004375)}{1-(1.004375)^{-360}}\) = 13239.61
The escrow payment is \(\frac{1}{12}\)(0.012)($2663995) = $2664.00. The total monthly payment is
$13,239.61 + $2,664 = $15,903.61.
b. How much is paid in interest over the life of the loan?
Answer:
The total amount paid is $13239.61(360) = $4766259.60, and the purchase price was $2,663,995. The amount of interest is the difference: $4, 766,259.60 – $2,663,995 = $2,102,264.60.
Question 3.
Suppose that you would like to buy a home priced at $200,000. You plan to make a payment of 10% of the purchase price and pay 1.2% of the purchase price into an escrow account annually.
a. Compute the total monthly payment and the total interest paid over the life of the loan for a 30-year mortgage at 4.8% annual interest.
Answer:
Using the payment formula with A = 0.9(200000) = 180000, i = \(\frac{0.048}{12}\)= 0.004, and n = 360, we have
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(180000)(0.004)}{1-(1.004)^{-360}}\) ≈ 994.40
The escrow payment is \(\frac{1}{12}\)(0.012)($200000) = $200.00. The total monthly payment is
$994.40 + $200 = $1,194.40.
The total amount of interest is the difference between the total amount paid, 360($994. 40), which is $357, 984, and the selling price $200, 000, so the total interest paid is $157,984.
b. Compute the total monthly payment and the total interest paid over the life of the loan for a 20-year mortgage at 4.8% annual interest.
Answer:
Using the payment formula with Ap = 0.9(200000) = 180000, i = \(\frac{0.048}{12}\) = 0.004, and n = 240, we have
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(180000)(0.004)}{1-(1.004)^{-240}}\) ≈ 1168. 12
The escrow payment is \(\frac{1}{12}\)(0.012)($200000) = $200.00. The total monthly payment is
$1,168.12 + $200 = $1,368.12.
The total amount of interest is the difference between the total amount paid, 240($1168. 12), which is $280,348.80, and the selling price, $200,000, so the total interest paid is $80,348.80.
c. Compute the total monthly payment and the total interest paid over the life of the loan for a 15-year mortgage at 4.8% annual interest.
Answer:
Using the payment formula with Ap = 0.9(200000) = 180000, i = \(\frac{0.048}{12}\) = 0.004, and n = 180, we have
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(180000)(0.004)}{1-(1.004)^{-180}}\) ≈ 1404.75
The escrow payment is \(\frac{1}{12}\)((0.012)($200000) = $200. 00. The total monthly payment is $1,404.75 + $200 = $1,604.75.
The total amount of interest is the difference between the total amount paid, 180($ 1404.75), which is $252,855, and the selling price, $200,000, so the total interest paid is $52,855.
Question 4.
Suppose that you would like to buy a home priced at $180,000. You qualify for a 30-year mortgage at 4.5% annual interest and pay 1.2% of the purchase price into an escrow account annually.
a. Calculate the total monthly payment and the total interest paid over the life of the loan if you make a 3% down payment.
Answer:
With a three percent down payment, you need to borrow = 0.97($180000) = $174600. We have
i = \(\frac{0.045}{12}\) =0.00375,and n = 360, so
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(174600)(0.00375)}{1-(1.00375)^{-360}}\) ≈ 884.67
The escrow payment is \(\frac{1}{12}\)((0.012)($180000) = $180.00. The total monthly payment is
$884.67 + $180 = $1,064.67.
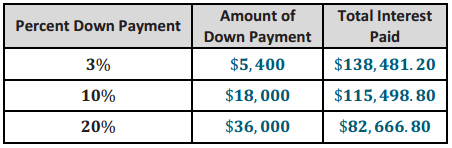
The total amount of interest is the difference between the total amount paid, 360($884.67), which is $318,481.20, and the selling price, $180,000, so the total interest paid is $138,481.20.
b. Calculate the total monthly payment and the total interest paid over the life of the loan if you make a 10% down payment.
Answer:
With a ten percent down payment, you need to borrow Ap = 0. 9($180000) = $162000. We have
i = \(\frac{0.045}{12}\) = 0.00375,and n = 360, so
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(162000)(0.00375)}{1-(1.00375)^{-360}}\) ≈ 820.83
The escrow payment is \(\frac{1}{12}\)(0. 012)($180000) = $180.00. The total monthly payment is
$820.83 + $180 = $1,000.83.
The total amount of interest is the difference between the total amount paid, 360($820. 83), which is $295, 498.80, and the selling price, $180, 000, so the total interest paid is $115, 498.80.
c. Calculate the total monthly payment and the total interest paid over the life of the loan if you make a 20% down payment.
Answer:
With a twenty percent down payment, you need to borrow Ap = 0.8($180000) = $144000. We have
i = \(\frac{0.045}{12}\) = 0.00375, and n = 360, so
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(144000)(0.00375)}{1-(1.00375)^{-360}}\) ≈ 729.63
The escrow payment is (0.012)($180000) = $180.00. The total monthly payment is $729.63 + $180 = $909. 63.
The total amount of interest is the difference between the total amount paid, 360($729.63), which is $262,666.80, and the selling price, $180,000, so the total interest paid is $82,666.80.
d. Summarize the results of parts (a), (b), and (c) in the chart below.
Answer:
Question 5.
The following amortization table shows the amount of payments to principal and interest on a $100,000 mortgage at the beginning and the end of a 30-year loan. These payments do not include payments to the escrow account.
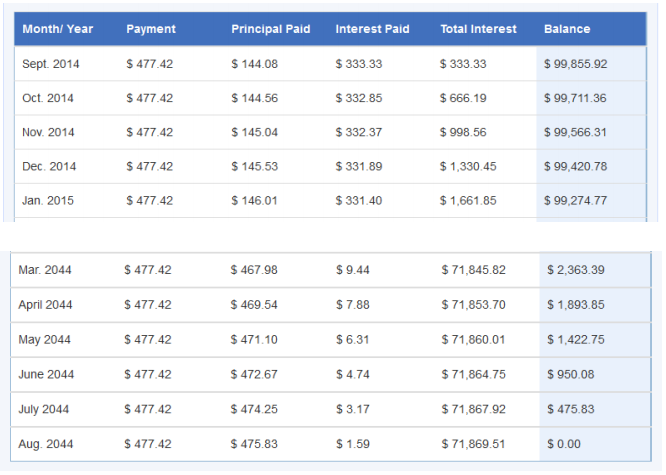
a. What is the annual interest rate for this loan? Explain how you know.
Answer:
Since the first interest payment is i . $100000 = $333.33, the monthly interest rate is i = 0.0033333, and the annual interest rate is then 12i ≈ 0.0399996, so i = 4.0%.
b. Describe the changes in the amount of principal paid each month as the month n gets closer to 360.
Answer:
As n gets closer to 360, the amount of the payment that is allocated to principal increases to nearly the amount of the entire payment.
c. Describe the changes in the amount of interest paid each month as the month n gets closer to 360.
Answer:
As n gets closer to 360, the amount of the payment that is allocated to interest decreases to nearly zero.
Question 6.
Suppose you want to buy a $200,000 home with a 30-year mortgage at 4.5% annual interest paying 10% down with an annual escrow payment that is 1.2% of the price of the home.
a. Disregarding the payment to escrow, how much do you pay toward the loan on the house each month?
Answer:
R = \(\frac{\mathbf{A}_{\mathbf{p}} \cdot \mathbf{i}}{\mathbf{1}-(\mathbf{1}+\mathbf{i})^{-n}}\)
= \(\frac{(180000)(0.00375)}{1-(1.00375)^{-360}}\) ≈ 912.03
The amount paid toward the loan on the house each month is $912.03.
b. What is the total monthly payment on this house?
Answer:
The monthly escrow payment is \(\frac{1}{12}\)(0.012)(200000) = 200, so the total monthly payment is $1,112.03.
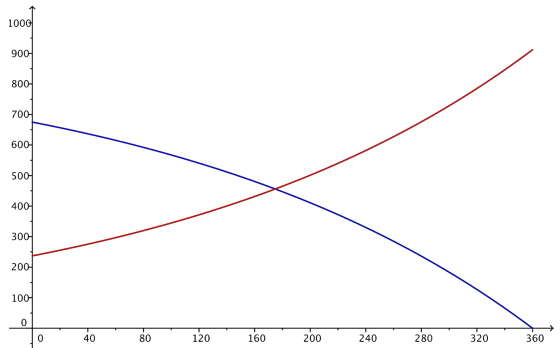
c. The graph below depicts the amount of your payment from part (b) that goes to the interest on the loan and the amount that goes to the principal on the loan. Explain how you can tell which graph is which.
Answer:
The amount paid to interest starts high and decreases, while the amount paid to principal starts low and then increases over the life of the loan. Thus, the blue curve that starts around 675 and decreases represents the amount paid to interest, and the red curve that starts around 240 and increases represents the amount paid to principal.
Question 7.
Student loans are very similar to both car loans and mortgages. The same techniques used for car loans and mortgages can be used for student loans. The difference between student loans and other types of loans is that usually students are not required to pay anything until 6 months after they stop being full-time students.
a. An unsubsidized student loan accumulates interest while a student remains In school. Sal borrows $9, 000 his first term in school at an interest rate of 5.95% per year compounded monthly and never makes a payment. How much will he owe 4\(\frac{1}{2}\) years later? How much of that amount is due to compounded interest?
Answer:
This is a compound interest problem without amortization since Sal does not make any payments.
9000 . (1 + \(\frac{0.0595}{12}\))54 ≈ 11755.40
Sal will owe $11,755.40 at the end of 4 years. Since he borrowed $9,000, he owes $2,755.40 in interest.
b. If Sal pays the Interest on his student loan every month while he Is in school, how much money has he paid?
Answer:
Since Sal pays the interest on his loan every month, the principal never grows. Every month, the interest is calculated by
9000 . \(\frac{0.0595}{12}\) ≈ $44.63.
if Sal pays $44.63 every month for 4\(\frac{1}{2}\) years, he will have paid $2,410.02.
c. Explain why the answer to part (a) is different than the answer to part (b).
Answer:
If Sal pays the Interest each month, as in part (b), then no interest ever compounds. if he skips the interest payments while he is in school, then the compounding process charges interest on top of interest, increasing the total amount of interest owed on the loan.
Question 8.
Considerthe sequence a0 = 10000, an = an – 1 . \(\frac{1}{10}\) for n ≥ 1.
a. Write the explicit form for the nth term of the sequence.
Answer:
a1 = 10000\(\frac{1}{10}\) = 1000
a2 = \(\frac{1}{10}\)(a1) = 10000 (\(\frac{1}{10}\))2
a3 = \(\frac{1}{10}\)(a2) = 10000 (\(\frac{1}{10}\))3
b. Evaluate \(\sum_{k=0}^{4} a_{k}\).
Answer:
\(\sum_{k=0}^{4} a_{k}\) = 10000 + 1000 + 100 + 10 + 1 = 11111
c. Evaluate \(\sum_{k=0}^{6} a_{k}\).
Answer:
\(\sum_{k=0}^{6} a_{k}\) = 10000 + 1000 + 100 + 10 + 1 + 0.1 + 0.01 = 11111.11
d. Evaluate \(\sum_{k=0}^{8} a_{k}\) using the sum of a geometric series formula.
Answer:
\(\sum_{k=0}^{8} a_{k}\) = 10000\(\frac{\left(1-r^{9}\right)}{1-r}\)
= 10000\(\frac{\left(1-\left(\frac{1}{10}\right)^{9}\right)}{1-\frac{1}{10}}\)
= 11,111.1111
e. Evaluate \(\sum_{k=0}^{10} a_{k}\) using the sum of a geometric series formula.
Answer:
\(\sum_{k=0}^{10} a_{k}\)) = 10000\(\frac{\left(1-r^{11}\right)}{1-r}\)
= 10000\(\frac{\left(1-\left(\frac{1}{10}\right)^{11}\right)}{1-\frac{1}{10}}\)
= 11111.111111
f. Describe the value of \(\sum_{k=0}^{n} a_{k}\) for any value of n ≥ 4.
Answer:
The value of \(\sum_{k=0}^{n} a_{k}\) for any n ≥ 4 is \(11111 . \underbrace{111 \ldots 1}_{n-4 \text { ones }} \).
Eureka Math Algebra 2 Module 3 Lesson 32 Exit Ticket Answer Key
Question 1.
Recall the present value of an annuity formula, where Ap is the present value, R is the monthly payment, i is the monthly interest rate, and n is the number of monthly payments:
Ap = R\(\left(\frac{1-(1+i)^{-n}}{i}\right)\)
Rewrite this formula to isolate R.
R = \(\frac{A_{p}}{\frac{1-(1+i)^{-n}}{i}}\)
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
Question 2.
Suppose that you want to buy a house that costs $175,000. You can make a 10% down payment, and 1.2% of the house’s value is paid into the escrow account each month.
a. Find the total monthly payment for a 30-year mortgage at 4.25% interest on this house.
Answer:
We haveAp = 0.9(175000) = 157500, and the monthly escrow payment is
\(\frac{1}{12}\)(o.012)($175000) = $175. The monthly interest rate ils given by i = \(\frac{0.045}{12}\) = 0.00375, and n = 12 . 30 = 360. Then the formula from Problem 1 gives
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(157500)(0.00375)}{1-(1.00375)^{-360}}\) ≈ 798.03
Thus, the payment to the loon is $798.03 each month. Then the total monthly payment is $798.03 + $175 = $973.03.
b. Find the total monthly payment for a 15-year mortgage at 3.75% interest on this house.
Answer:
We have Ap = 0.9(175000) = 157500, and the monthly escrow payment is
\(\frac{1}{12}\)(o.012) ($175000) = $175. The monthly interest rate i is given by i = \(\frac{0.0375}{12}\) = 0.003125, and n = 12 . 15 = 180. Then the formula from Problem 1 gives
R = \(\frac{A_{p} \cdot i}{1-(1+i)^{-n}}\)
= \(\frac{(157500)(0.003125)}{1-(1.003125)^{-180}}\) ≈ 1145.38
Thus, the payment to the loan is $1, 145.38 each month. Then the total monthly payment is
$1, 145.38 + $175 = $1,320.38.