Engage NY Eureka Math Algebra 2 Module 3 Lesson 20 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 20 Opening Exercise Answer Key
Opening Exercise:
a. Sketch the graphs of the three functions f(x) = x2, g(x) = (2x)2 + 1, and h(x) = 4x2 + 1.
i. Describe the sequence of transformations that takes the graph of f(x) = x2 to the graph of g(x) = (2x)2 + 1.
Answer:
The graph of g is a horizontal scaling by a factor of \(\frac{1}{2}\) and a vertical translation up 1 unit of the graph of f.
ii. Describe the sequence of transformations that takes the graph of f(x) = x2 to the graph of h(x) = 4x2 + 1.
Answer:
The graph of h is a vertical scaling by a factor of 4 and a vertical translation up 1 unit of the graph of f.
iii. Explain why g and h from parts (I) and (ii) are equivalent functions.
Answer:
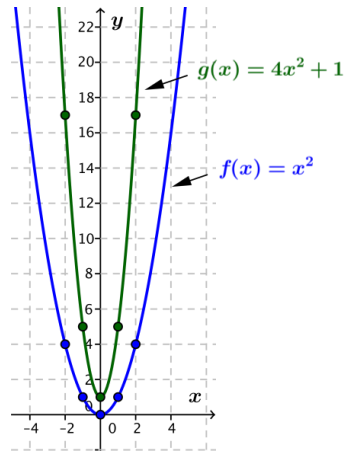
These functions are equivalent and have the same graph because the expressions (2x)2 + 1 and 4x2 + 1 are equivalent. The blue graph shown is the graph off, and the green graph is the graph of g and h.
b. Describe the sequence of transformations that takes the graph of f(x) = sin(x) to the graph of g(x) = sin(2x) – 3.
Answer:
The graph of g is a horizontal scaling by a factor of \(\frac{1}{2}\) and a vertical translation down 3 units of the graph of f.
c. Describe the sequence of transformations that takes the graph of f(x) = sin(x) to the graph of h(x) = 4 sin(x) – 3.
Answer:
The graph of h is a vertical scaling by a factor of 4 and a vertical translation down 3 units of the graph of f.
d. Explain why g and h from parts (b) – (c) are not equivalent functions.
Answer:
These functions are not equivalent because they do not have the same graphs, and the two expressions are not equivalent.
Eureka Math Algebra 2 Module 3 Lesson 20 Exploratory Challenge Answer Key
Exploratory Challenge:
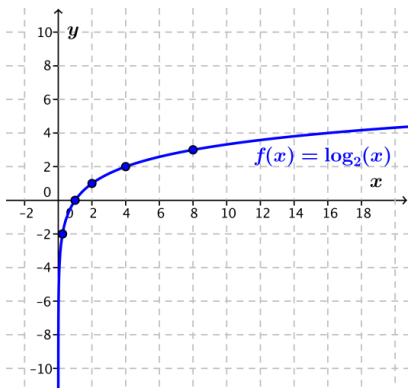
a. Sketch the graph of f(x) = log2(x) by identifying and plotting at least five key points. Use the table below to get started.
| x | Log2(x) |
| \(\frac{1}{4}\) | -2 |
| \(\frac{1}{2}\) | -1 |
| 1 | |
| 2 | |
| 4 | |
| 8 |
Answer:
The graph of f is shown below.
| x | Log2(x) |
| \(\frac{1}{4}\) | -2 |
| \(\frac{1}{2}\) | -1 |
| 1 | 0 |
| 2 | 1 |
| 4 | 2 |
| 8 | 3 |
b. Describe a sequence of transformations that takes the graph off to the graph of g(x) = log2(8x).
Answer:
The graph of g is a horizontal scaling by a factor of \(\frac{1}{8}\) of the graph of f.
c. Describe a sequence of transformations that takes the graph off to the graph of h(x) = 3 + log2(x).
Answer:
The graph of h is a vertical translation up 3 units of the graph of f.
d. Complete the table below for f, g, and h and describe any noticeable patterns.
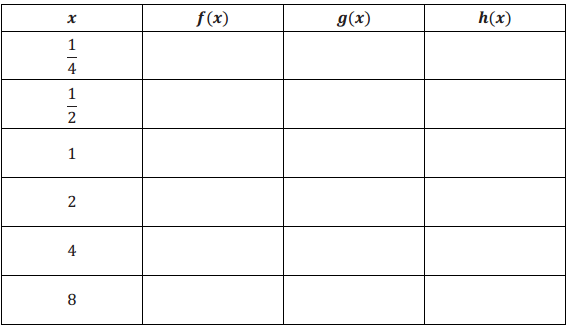
Answer:
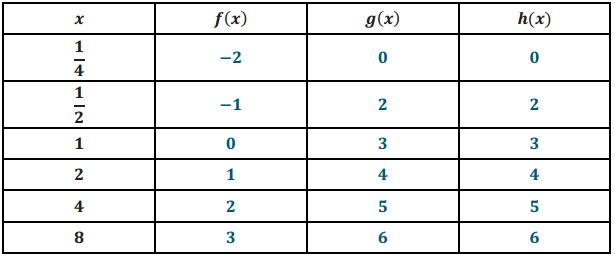
The functions g and h have the same range values at each domain value in the table.
e. Graph the three functions on the same coordinate axes and describe any noticeable patterns.
Answer:
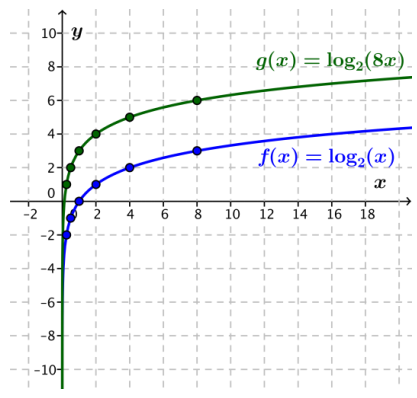
The graphs of g and h are identical.
f. Use a property of logarithms to show that g and h are equivalent.
Answer:
By the product property and the definition of logarithm, log2(8x) = log2(8) + log2(x) = 3 + log2(x), so g(x) = h(x) for all positive real numbers x and g and h are equivalent functions.
g. Describe the graph of p(x) = log2(\(\frac{x}{4}\)) as a vertical translation of the graph of f(x) = log2(x). Justify your response.
Answer:
The graph of p isa vertical translation down 2 units of the graph off because log2(\(\frac{x}{4}\)) = log2(x) – 2.
h. Describe the graph of h(x) = 3 + log2(x) as a horizontal scaling of the graph of f(x) = log2(x). Justify your response.
Answer:
The graph of h is a horizontal scaling by a factor of \(\frac{1}{8}\) of the graph of f because
3 + log2(x)= log2(8) + log2(x)= log2(8x).
i. Do the functions h(x) = log2(8) + log2(x) and k(x) = log2(x + 8) have the same graphs? Justify your reasoning.
Answer:
No, they do not. By substituting 1 for x in both f and g, you can see that the graphs of the two functions do not have the same y-coordinate at this point. Therefore, the graphs cannot be the same if at least one point is different.
j. Use properties of exponents to explain why graphs of f(x) = 4x and g(x) = (22)x are identical.
Answer:
Using the power property of exponents, 22x = (22)x = 4x Since the expressions are equal, the graphs of the functions would be the same.
k. Use the properties of exponents to predict what the graphs of g(x) = 4 . 2x and h(x) = 2x + 2 look like compared to one another. Describe the graphs of g and h as transformations of the graph of f(x) = 2x. Confirm your prediction by graphing f, g, and h on the same coordinate axes.
Answer:
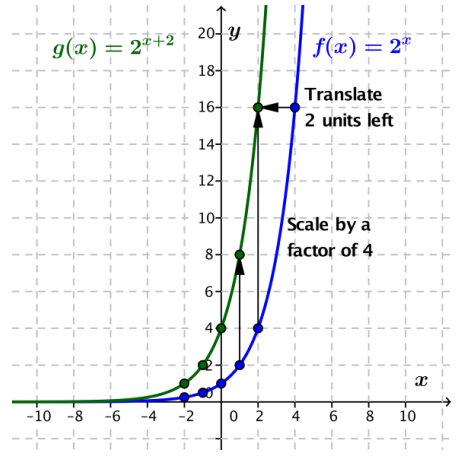
The graphs of the two functions g and h are the same since 2x + 2 = 2x . 22 = 4. 2x by the multiplication property of exponents and the commutative property. The graph of g is the graph of f(x) = 2x scaled vertically by a factor of 4. The graph of h is the graph of f(x) = 2x translated horizontally 2 units to the left.
l. Graph f(x) = 2x, g(x) = 2-x and h(x) = (\(\frac{1}{2}\))x on the same coordinate axes. Describe the graphs of g and h as transformations of the graph off. Use the properties of exponents to explain why g and h are equivalent.
Answer:
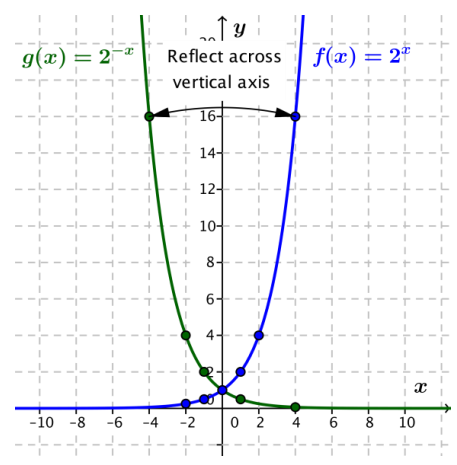
The graph of g and the graph of h are both reflections about the vertical axis of the graph of f. They are equivalent because ((\(\frac{1}{2}\)))x = (2-1)-x = 2-x by the definition of a negative exponent and the power property of exponents.
Eureka Math Algebra 2 Module 3 Lesson 20 Example Answer Key
Example 1: Graphing Transformations of the Logarithm Functions
The general form of a logarithm function is given by f(x) = k + a log(x – h), where a, b, k, and h are real numbers such that b is a positive number not equal to 1, and x – h > 0.
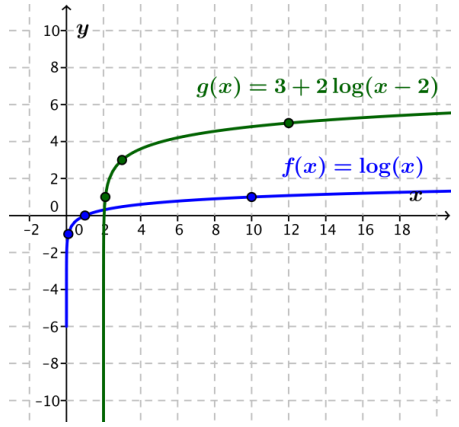
a. Given g(x) = 3 + 2 log(x – 2), describe the graph of g as a transformation of the common logarithm function.
Answer:
The graph of g is a horizontal translation 2 units to the right, a vertical scaling by a factor of 2, and a vertical translation up 3 units of the graph of the common logarithm function.
b. Graph the common logarithm function and g on the same coordinate axes.
Answer:
Example 2: Graphing Transformations of Exponential Functions
The general form of the exponential function is given by f(x) = a . bx + k, where a, b, and k are real numbers such that b is a positive number not equal to 1.
a. Use the properties of exponents to transform the function g(x) = 32x + 1 – 2 to the general form, and then graph it. What are the values of a, b, and k?
Answer:
Using the properties of exponents, 32x + 1 – 2 = 32x . 31 – 2 = 3 . 9x – 2. Thus, g(x) = 3(9)x – 2 so a = 3, b = 9, and k = -2.
b. Describe the graph of g as a transformation of the graph of f(x) = 9x.
Answer:
The graph of g is a vertical scaling by a factor of 3 and a vertical translation down 2 units of the graph of f.
c. Describe the graph of g as a transformation of the graph of f(x) = 3x.
Answer:
The graph of g is a horizontal scaling by a factor of \(\frac{1}{2}\), a vertical scaling by a factor of 3, and a vertical translation down 2 units of the graph of f.
d. Sketch the graph of g using transformations.
Answer:
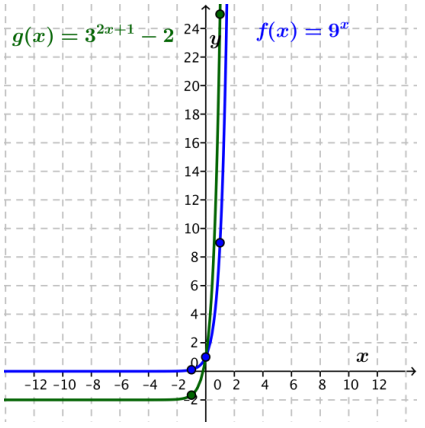
The graph of f(x) = 9x is shown in blue, and the graph of g is shown in green.
Eureka Math Algebra 2 Module 3 Lesson 20 Exercise Answer Key
Exercises:
Graph each pair of functions by first graphing f and then graphing g by applying transformations of the graph of f. Describe the graph of g as a transformation of the graph of f.
Exercise 1.
f(x) = log3(x) and g(x) = 2 log3(x – 1)
Answer:
The graph of g is the graph of f translated 1 unit to the right and stretched vertically by a factor of 2.
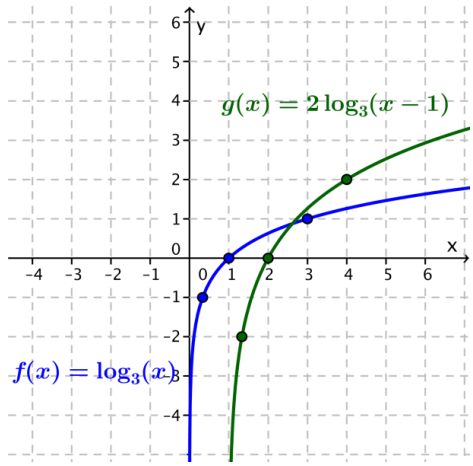
Exercise 2.
f(x) = log(x) and g(x) = log(100x)
Answer:
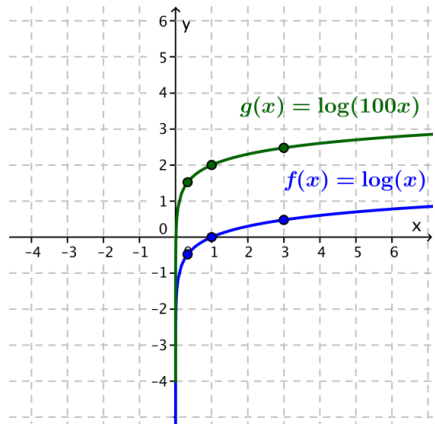
Because of the product property of logarithms, g(x) = 2 + log(x). The graph of g is the graph of f translated vertically 2 units.
Exercise 3.
f(x) = log5x and g(x) = – log5(5(x + 2))
Answer:
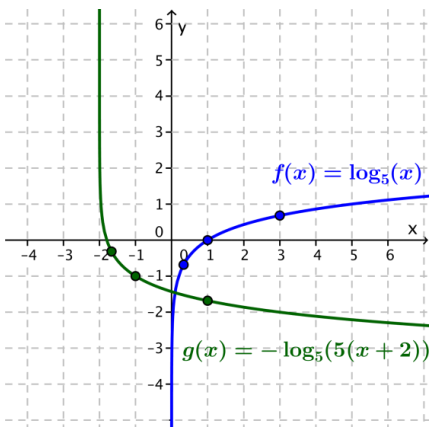
Since -log5(5(x + 2)) = -1 – log5(x + 2) by the product property of logarithms and the distributive property, the graph of gis the graph off translated 2 units to the left, reflected across the horizontal axis, and translated down 1 unit.
Exercise 4.
f(x) = 3x and g(x) = -2 . 3x – 1
Answer:
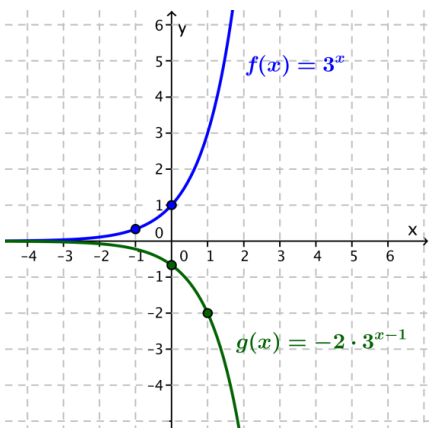
Since -2 . 3x – 1 = -2 . 3x. 3x – 1 = –\(\frac{2}{3}\) . 3x by the properties of exponents and the commutative property, the graph of g is the graph of f reflected across the horizontal axis and compressed by afactor of \(\frac{2}{3}\).
There are multiple ways to obtain the graph of g from the graph of f through a sequence of transformations. One choice is to use the structure of g(x) = -2 . 3x – 1to translate the graph off horizontally one unit left, reflect across the horizontal axis, and then scale vertically by a factor of 2. Another choice is to rewrite g(x) as g(x) = \(\frac{2}{3}\)(3x). Then the graph of g is obtained from the graph of f by reflecting the graph of f across the horizontal axis and then vertically scaling by a factor of \(\frac{2}{3}\).
Eureka Math Algebra 2 Module 3 Lesson 20 Problem Set Answer Key
Question 1.
Describe each function as a transformation of the graph of a function in the form f(x) = log(x). Sketch the graph of f and the graph of g by hand. Label key features such as intercepts, intervals where g is increasing or decreasing, and the equation of the vertical asymptote.
a. g(x) = log2(x – 3)
Answer:
The graph of g is the graph of f(x) = log2(x) translated horizontally 3 units to the right. The function g is increasing on (3, ∞). The x-intercept is 4, and the vertical asymptote is x = 3.
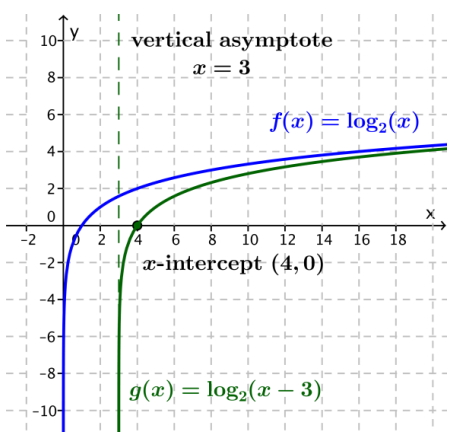
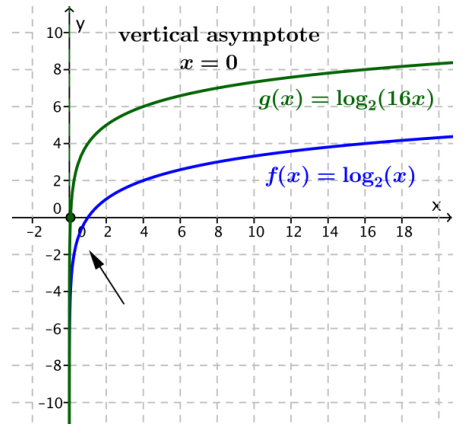
b. g(x) = log2(16x)
Answer:
The graph of g is the graph of f(x) = log2(x) translated vertically up 4 units. The function g is increasing on
(0, ∞). The x-intercept is 2-4. The vertical asymptote is x = 0.
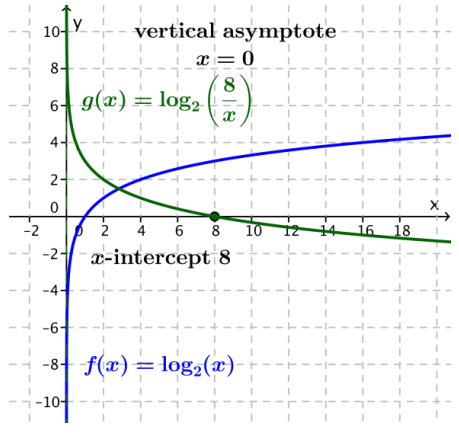
c. g(x) = log2(\(\frac{8}{x}\))
Answer:
The graph of g is the graph of f(x) = log2(x) reflected about the horizontal axis and translated vertically up 3 units. The function g is decreasing on (0, ∞). The x-intercept is 23. The vertical asymptote is x = 0. The reflected graph and the final graph are both shown in the solution.
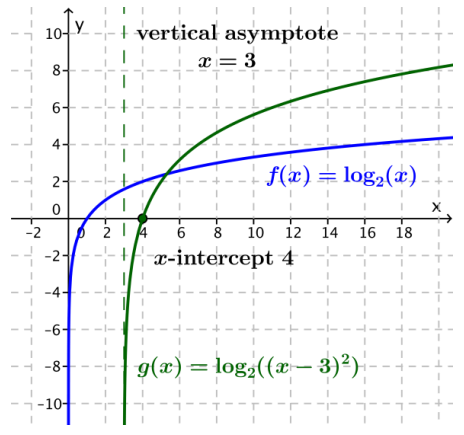
d. g(x) = log2((x – 3)2)for x > 3
Answer:
The graph of g is the graph of f(x) = log2(x) stretched vertically by a factor of 2 and translated horizontally 3 units to the right. The function g is increasing on (3, ∞). The x-intercept is 4, and the vertical asymptote is x = 3.
Question 2.
Each function graphed below can be expressed as a transformation of the graph of f(x) = log(x). Write an algebraic function for g and h, and state the domain and range.
Answer:
In Figure 1, g(x) = -log(x – 2) for x > 2. The domain of g is x > 2, and the range of g is all real numbers.
In Figure 2, h(x) = 2 + log(x) for x > 0. The domain of h is x > 0, and the range of h is all real numbers.
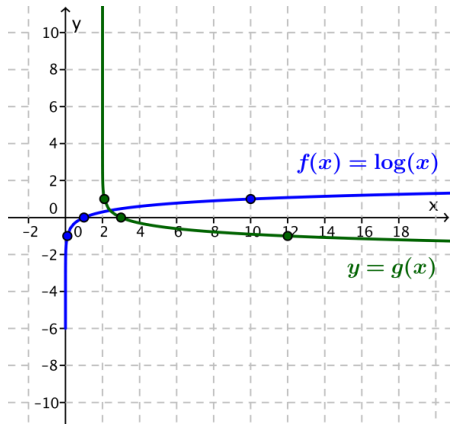
Figure 1: Graphs of f(x) = log(x) and the function g
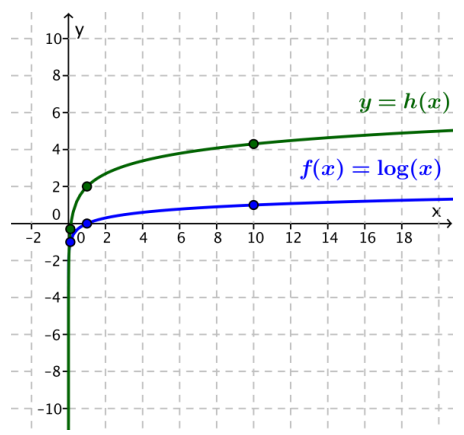
Figure 2: Graphs of f(x) = log(x) and the function h
Question 3.
Describe each function as a transformation of the graph of a function in the form f(x) = bx. Sketch the graph off and the graph of g by hand. Label key features such as intercepts, intervals where g is increasing or decreasing, and the horizontal asymptote.
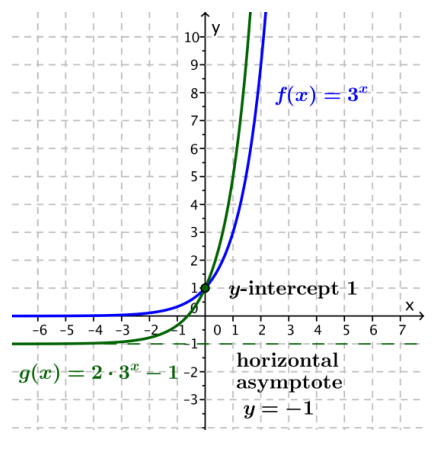
a. g(x) = 2 . 3x – 1
Answer:
The graph of g is the graph of f(x) = 3x scaled vertically by a factor of 2 and translated vertically down 1 unit. The equation of the horizontal asymptote is y = -1. The y-intercept is 1, and the x-intercept is approximately -0.631. The function g is increasing for all real numbers.
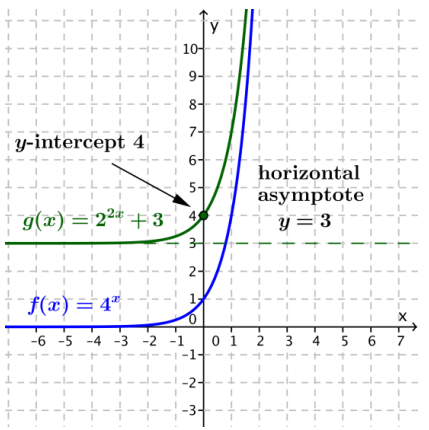
b. g(x) = 22x + 3
Answer:
The graph of g is the graph of f(x) = 4x translated vertically up 3 units. The equation of the horizontal asymptote is y = 3. The y-intercept is 4. There is no x-intercept. The function g is increasing for all real numbers.
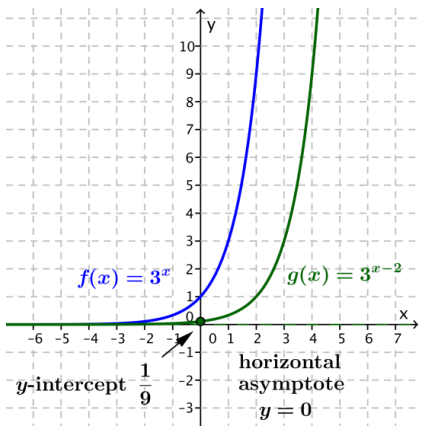
c. g(x) = 3x – 2
Answer:
The graph of g is the graph of f(x) = 3x translated horizontally 2 units to the right OR the graph of f scaled
vertically by a factor of \(\frac{1}{9}\). The equation of the horizontal asymptote is y = 0. The y-intercept is \(\frac{1}{9}\). There is no x-intercept, and the function g is increasing for all real numbers.
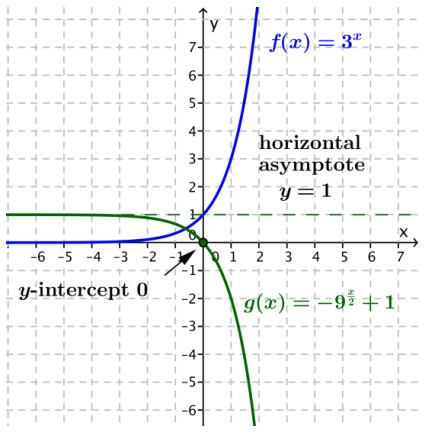
d. g(x) = -9\(\frac{x}{2}\) + 1
Answer:
The graph of g is the graph of f(x) = 3x reflected about the horizontal axis and then translated vertically up 1 unit. The equation of the horizontal asymptote is y = 1. The y-intercept is 0, and the x-intercept is also 0. The function g is decreasing for all real numbers.
Question 4.
Using the function f(x) = 2x, create a new function g whose graph is a series of transformations of the graph of f with the following characteristics:
→ The function g is decreasing for all real numbers.
→ The equation for the horizontal asymptote is y = 5.
→ The y-intercept is 7.
Answer:
One possible solution is g(x) = 2 . 2-x + 5.
Question 5.
Using the function f(x) = 2x, create a new function g whose graph is a series of transformations of the graph of f with the following characteristics:
→ The function g is increasing for all real numbers.
→ The equation for the horizontal asymptote is y = 5.
→ The y-intercept is 4.
Answer:
One possible solution is g(x) = -(2-x) + 5.
Question 6.
Consider the function g(x) = (\(\frac{1}{4}\))x – 3
a. Write the function g as an exponential function with base 4. Describe the transformations that would take the graph of f(x) = 4x to the graph of g.
Answer:
(\(\frac{1}{4}\))x – 3 = (4-1)x – 3 = 4-x + 3 = 43 . 4-x
Thus, g(x) = 64 . 4-x. The graph of g is the graph of f reflected about the vertical axis and scaled vertically
by a factor of 64.
b. Write the function g as an exponential function with base 2. Describe two different series of transformations that would take the graph of f(x) = 2’ to the graph of g.
Answer:
(\(\frac{1}{4}\))x – 3 = (2)-2x – 3 = 2-2(x – 3) = 2-2x + 6 = 64 . 2-2x
Thus, g(x) = 64 . 2-2x or g(x) = 2-2(x – 3). To obtain the graph of g from the graph of f, you can scale the graph horizontally by a factor of \(\frac{1}{2}\), reflect the graph about the vertical axis, and scale it vertically by a factor of 64. Or, you can scale the graph horizontally by a factor of \(\frac{1}{2}\), reflect the graph about the vertical axis, and translate the resulting graph horizontally 3 units to the right.
Question 7.
Explore the graphs of functions in the form f(x) = log(xn) for n > 1. Explain how the graphs of these functions change as the values of n increase. Use a property of logarithms to support your reasoning.
Answer:
The graphs appear to be a vertical scaling of the common logarithm function by a factor of n. This is true because of the property of logarithms that states log(xn) = n log(x).
Question 8.
Use a graphical approach to so’ve each equation. If the equation has no solution, explain why.
a. log(x) = log(x – 2)
Answer:
This equation has no solution because the graphs of y = log(x) and y = log(x – 2) are horizontal translations of each other. Thus, their graphs do not intersect, and the corresponding equation has no solution.
b. log(x) = log(2x)
Answer:
This equation has no solution because log(2x) = log(2) + log(x), which means that the graphs of y = log(x) andy = log(2x) are a vertical translation of each other. Thus, their graphs do not intersect, and the corresponding equation has no solution.
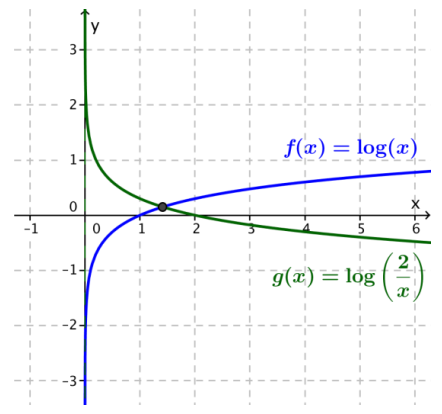
c. log(x) = log (\(\frac{2}{x}\))
Ans:
The solution is the x-coordinate of the intersection point of the graphs of y = log(x) and y = log(2) – log(x). Since the graph of the function defined by the right side of the equation is a reflection across the horizontal axis and a vertical translation of the graph of the function defined by the left side of the equation, the graphs of these functions intersect in exactly one point with an x-coordinate approximately 1.5.
d. Show algebraically that the exact solution to the equation in part (c) is √2.
Answer:
log(x) = log(2) – log(x)
2 log(x) = log(2)
log(x) = \(\frac{1}{2}\)log(2)
log(x) = log(2\(\frac{1}{2}\))
x = 2\(\frac{1}{2}\)
Since 2\(\frac{1}{2}\) = √2 the exact solution is √2.
Question 9.
Make a table of values forf(x) = \(x^{\frac{1}{\log (x)}}\) for x > 1. Graph the function f for x > 1. Use properties of logarithms to explain what you see in the graph and the table of values.
Answer:

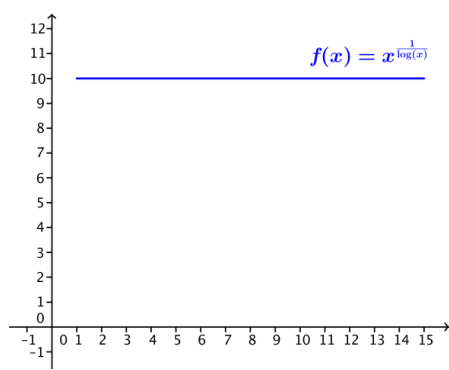
We see that \(x^{\frac{1}{\log (x)}}\) = 10 for all x > 1 because \(\frac{1}{\log (x)}=\frac{\log (10)}{\log (x)}\) = logx(10). Therefore, when we substitute logx(10) into the expression \(x^{\frac{1}{\log (x)}}\), we get xlogx(10), which is equal to 10 according to the definition of a logarithm.
Eureka Math Algebra 2 Module 3 Lesson 20 Exit Ticket Answer Key
Question 1.
Express g(x) = -log4(2x) in the general form of a logarithmic function, f(x) = k + a logb(x – h). Identify a, b, h, and k.
Answer:
Since -log4(2x) = -log4(2) + log4(x) = –\(\frac{1}{2}\) – log4(x), the function is g(x) = –\(\frac{1}{2}\) – log(x), and a = -1, b = 4, h = 0, and k = –\(\frac{1}{2}\).
Question 2.
Use the structure of g when written in general form to describe the graph of g as a transformation of the graph of h(x) = log4(x).
Answer:
The graph of g is the graph of h reflected about the horizontal axis and translated down \(\frac{1}{2}\) unit.
Question 3.
Graph g and h on the same coordinate axes.
Answer:
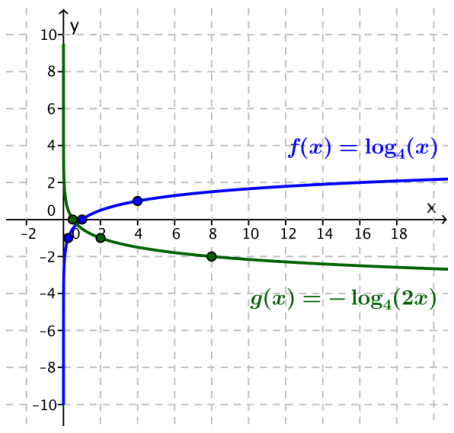
The graph of h is shown in blue, and the graph of g is shown in green.