Engage NY Eureka Math Algebra 2 Module 3 Lesson 16 Answer Key
Eureka Math Algebra 2 Module 3 Lesson 16 Opening Exercise Answer Key
a. Explain how to use a number line to add the fractions \(\frac{7}{5}\) + \(\frac{9}{4}\).
Answer:
First, we locate the point \(\frac{7}{5}\) on the number line by dividing each unit into 5 intervals of length \(\frac{1}{5}\).

Then, we locate the point \(\frac{9}{4}\) on the number line by dividing each unit into 4 intervals of length \(\frac{1}{4}\).

To find the sum, we place the green segment of length \(\frac{9}{4}\) end-to-end with the blue segment of lenth \(\frac{7}{5}\) and the right end point of the green segment ¡s the sum. Since the tick marks at units of \(\frac{1}{4}\) and \(\frac{1}{5}\) do not align, we make new tick marks that are \(\frac{1}{20}\) apart. Then \(\frac{7}{5}\) = \(\frac{28}{20}\) and \(\frac{9}{4}\) = \(\frac{45}{20}\) so the sum is located at point \(\frac{73}{20}\)

b. Convert \(\frac{7}{5}\) and \(\frac{9}{4}\) to decimals, and explain the process for adding them together.
Answer:
We know that \(\frac{7}{5}\) = 1.4 and \(\frac{9}{4}\) = 2.25. To add these numbers, we add a zero placeholder to 1.4 to get 1.40 so that each number has the same number of decimal places. Then, we line them up at the decimal place and add from right to left, carrying over power of 10 if needed (we do not need to carry for this sum).
Step 1: Working from right to left, we first add 0 hundredths + 5 hundredths = 5 hundredths.
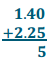
Step 2: Then we add 4 tenths +2 tenths = 6 tenths.
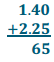
Step 3: And, finally, we add 1 one + 2 ones = 3 ones.
![]()
Eureka Math Algebra 2 Module 3 Lesson 16 Exercise Answer Key
Exercises:
Exercise 1.
According to the calculator, log(4) = 0.6020599913 … and log(25) = 1.3979400087 …. Find an approximation of log(4) + log(25) to one decimal place, that ¡s, to an accuracy of 10-1.
Answer:
0.60 < log(4) < 0.61
1.39 < log(25) < 1.40
1.99 < log(4) + log(25) < 2.01
log(4) + log(25) ≈ 2.0
Exercise 2.
Find the value of log(4) + log(25) to an accuracy of 10-2.
Answer:
0.602 < log(4) < 0.603
1.397 < log(25) < 1.398
1.999 < log(4) + log(25) < 2.001
log(4) + log(25) ≈ 2.00
Exercise 3.
Find the value of log(4) + log(25) to an accuracy of 10_8.
Answer:
0. 602059991 ≤ log(4) ≤ 0. 602059992
1.397940008 ≤ log(25) ≤ 1.397940009
1. 999999999 ≤ log(4) + log(25) ≤ 2.000000001
log(4) + log(25) ≈ 2.00000000
Exercise 4.
Make a conjecture: Is log(4) + log(25) a rational or an irrational number?
Answer:
It appears that log(4) + log(25) = 2 exactly, so my conjecture is that log(4) + log(25) is a rational number.
Exercise 5.
Why is your conjecture in Exercise 4 true?
Answer:
The logarithm rule that says log(x) + log(y) = log(xy) applies here.
log(4) + log(25) = log(4 . 25)
= log(100)
= log(102)
= 2
Remember that the calculator gives the following values: log(4) = 0.6020599913 … and log(25) = 1.3979400087…
Exercise 6.
Find the value of log(4) log(25) to three decimal places.
Answer:
0.6020 ≤ log(4) ≤ 0.6021
1. 3979 ≤ log(25) ≤ 1.3980
0.8415358 ≤ log(4) . log(25) ≤ 0.8417358
log(4) log(25) ≈ 0.842
Exercise 7.
Find the value of log(4) log(25) to five decimal places.
Answer:
0.602059 ≤ log(4) ≤ 0.602060
1.397940 < log(25) ≤ 1.397941
0.8416423585 ≤ log(4) . log(25) ≤ 0.8416443585
log(4) log(25) ≈ 0.84164
Exercise 8.
Does your conjecture from the above discussion appear to be true?
Answer:
No. The work from Exercise 6 shows that log(4) . log(25) ≠ log(29), and log(4) . log(25) ≠ log(100). (Answers will vary based on student conjectures.)
Eureka Math Algebra 2 Module 3 Lesson 16 Problem Set Answer Key
Question 1.
Given that √5 ≈ 2.2360679775 and π ≈ 3. 1415926535, find the sum √5 + π to an accuracy of 10-8 without using a calculator.
Answer:
From the estimations we are given, we know that
2.236067977 < √5 < 2.236067978
3.141592653 < π < 3.141592654.
Adding these together gives
5.377660630 < √5 + π < 5.377660632.
Then, to an accuracy of 10-8, we have
√5 + π ≈ 5. 37766063.
Question 2.
Put the following numbers in order from least to greatest. √2, π, 0, e, \(\frac{22}{7}\), \(\frac{\pi^{2}}{3}\), 3.14, √10
Answer:
0, √2, e, 3.14, π, \(\frac{22}{7}\), √10, \(\frac{\pi^{2}}{3}\)
Question 3.
Find a rational number between the specified two numbers.
a. \(\frac{4}{13}\) \(\frac{5}{13}\)
Answer:
Many answers are possible. Since \(\frac{4}{13}\) = \(\frac{8}{26}\) and \(\frac{5}{13}\) = \(\frac{10}{26}\), we know that \(\frac{4}{13}\) < \(\frac{9}{26}\) < \(\frac{5}{13}\).
b. \(\frac{3}{8}\) and \(\frac{5}{9}\)
Answer:
Many answers are possible. Since \(\frac{3}{8}\) = \(\frac{27}{72}\) and \(\frac{5}{9}\) = \(\frac{40}{72}\) we know that \(\frac{30}{72}\) = \(\frac{5}{12}\) is between \(\frac{3}{8}\) and \(\frac{5}{9}\).
c. 1.7299999 and 1.73
Answer:
Many answers are possible. 1.7299999 < 1.72999995 < 1.73.
d. \(\frac{\sqrt{2}}{7}\) and \(\frac{\sqrt{2}}{9}\)
Answer:
Many answers are possible. Since \(\frac{\sqrt{2}}{9}\) ≈ 0.157135 and \(\frac{\sqrt{2}}{7}\) ≈ 0.202031, we know \(\frac{\sqrt{2}}{9}\) < 0.2 < \(\frac{\sqrt{2}}{7}\).
e. π and √10
Answer:
Many answers are possible. Since π ≈ 3. 14159 and √10 ≈ 3.16228, we know π < 3.15 < √10.
Question 4.
Knowing that is irrational, find an irrational number between and
Answer:
One such number is r√2, for some rational number r. Then \(\frac{1}{2}\) < r√2 <\(\frac{5}{9}\) so we have \(\frac{1}{2 \sqrt{2}}\) < r < \(\frac{5}{9 \sqrt{2}}\) Since \(\frac{1}{2 \sqrt{2}}\) ≈ 0. 3536 and \(\frac{5}{9 \sqrt{2}}\) ≈ 0.3929, we can let r = 0.36. Then, 0. 36√2 is an irrational number between \(\frac{1}{2}\) and \(\frac{5}{9}\).
Question 5.
Give an example of an irrational number between e and π.
Answer:
Many answers are possible, such as \(\frac{\pi+e}{2}\), \(\sqrt{\pi e}\) or \(\frac{10}{11}\)π.
Question 6.
Given that √2 is irrational, which of the following numbers are irrational?
\(\frac{\sqrt{2}}{2}\), 2 + √2, \(\frac{\sqrt{2}}{2 \sqrt{2}}\), \(\frac{2}{\sqrt{2}}\), (√2)2.
Answer:
Note that \(\frac{\sqrt{2}}{2 \sqrt{2}}\) = \(\frac{1}{2}\), \(\frac{2}{\sqrt{2}}\) = √2 and (√2)2 = 2. The numbers \(\frac{\sqrt{2}}{2}\), 2 + √2 and \(\frac{2}{\sqrt{2}}\) are irrational.
Question 7.
Given that π is irrational, which of the following numbers are irrational?
\(\frac{\pi}{2}\), \(\frac{\pi}{2 \pi}\), √π, π2
Answer:
The numbers \(\frac{\pi}{2}\), √π, π2 are irrational.
Question 8.
Which of the following numbers are irrational?
1, 0, √5, \(\sqrt[3]{64}\), e, π, \(\frac{\sqrt{2}}{2}\), \(\frac{\sqrt{8}}{\sqrt{2}}\), cos(\(\frac{\pi}{3}\)), sin(\(\frac{\pi}{3}\))
Answer:
The numbers √5, e, π, \(\frac{\sqrt{2}}{2}\), and sin(\(\frac{\pi}{3}\)) are irrational.
Question 9.
Find two irrational numbers x and y so that their average is rational.
Answer:
If x = 1 + √2 and y = 3 – √2 then \(\frac{x+y}{2}\) = \(\frac{1}{2}\)((1+ √2)) + (3 – √2) = 2. So, the average of x and y is rational.
Question 10.
Suppose that \(\frac{2}{3}\)x is an irrational number. Explain how you know that x must be an irrational number. (Hint: What would happen if there were integers a and b so that x = \(\frac{a}{b}\)?
Answer:
If x is rational, then there are integers a and b so that x = \(\frac{a}{b}\). Then \(\frac{2a}{2b}\) is rational, so \(\frac{2}{3}\)x is also rational. This contradicts the given fact that x is irrational, so it is not possible for x to be rational. Thus, x must be an irrational number.
Question 11.
If r and s are rational numbers, prove that r + s and r – s are also rational numbers.
Answer:
¡fr and s are rational numbers, then there exist integers a, b, c, d with b ≠ 0 and d ≠ 0 so that r = \(\frac{a}{b}\) and s = \(\frac{c}{d}\). Then,
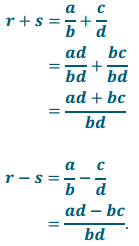
Since ad + bc, ad – bc, and bd are integers, r + s and r – s are rational numbers.
Question 12.
If r is a rational number and x is an irrational number, determine whether the following numbers are always rational, sometimes rational, or never rational. Explain how you know.
a. r + x
Answer:
If r + x = y and y ¡s rational, then r – y = -x would be rational by Problem 11. Since x is irrational, we know -x ¡s irrational, so y cannot be rational. Thus, the sum r + x ¡s never rational.
b. r – x
Answer:
If r – x = y, and y are rational, then r – y = x would be rational by Problem 11. Since x is irrational, y cannot be rational. Thus, the difference r – x is never rational.
c. rx
Answer:
If rx = y, r ≠ 0, and y is rational, then there are integers a, b, c, d with a ≠ 0, b ≠ 0, and d ≠ 0 so that r = \(\frac{a}{b}\) and y = \(\frac{c}{d}\). Then x = \(\frac{y}{r}\) = \(\frac{cb}{ad}\), so x is rational. Since x was not rational, the only way that rx can be rational ¡s ¡f r = 0. Thus, rx ¡s sometimes rational (in only one case).
d. xr
Answer:
If x = \(\sqrt[r]{\boldsymbol{k}}\) for some rational number k, then xr = k is rational. For example, (√5)2 = 5 is rationaL But, πr is never rational for any exponent r, so xr is sometimes rational.
Question 13.
If x and y are irrational numbers, determine whether the following numbers are always rational, sometimes rational, or never rational. Explain how you know.
a. x + y
Answer:
This ¡s sometimes rational. For example, π + √2 ¡s irrational, but (1 + √2) + (1 -√2) = 2 is rational.
b. x – y
Answer:
This is sometimes rational. For example, π – √2 ¡s irrational, but (5 + √3) – (1 +√3) = 4 is rational.
c. xy
Answer:
This is sometimes rational. For example, π√2 is irrational, but √2 . √8 = 4 is ratuional.
d. \(\frac{x}{y}\)
Answer:
This is sometimes rational. For example, \(\frac{\pi}{\sqrt{2}}\) is irrational, but \(\frac{\sqrt{8}}{\sqrt{2}}\) = 2 is rational.
Eureka Math Algebra 2 Module 3 Lesson 16 Exit Ticket Answer Key
Question 1.
The decimal expansions of e and √5 are given below.
e ≈ 2.71828182 …
√5 ≈ 2.23606797…
a. Find an approximation of √5 + e to three decimal places. Do not use a calculator.
Answer:
2.2360 ≤ √5 2.2361
2. 7182 ≤ e ≤ 2.7183
4.9542 √5 + e ≤ 4.9544
Thus, to three decimal places, √5 + e ≈ 4.954.
b. Explain how you can locate √5 + e on the number line. How is this different from locating 2.6 + 2.7 on the number line?
Answer:
We cannot locate √5 + e precisely on the number line because the sum ¡s irrational, but we can get as close to it as we want by squeezing it between two rational numbers, r1 and r2, that differ only in the last decimal place, r1 + √5+ e ≤ r2. Since we can locate rational numbers on the number line, we can get arbitrarily close to the true location of √5 + e by starting with more and more accurate decimal representations of √5b and e.
This differs from pinpointing the location of sums of rational numbers because we can precisely locate the sum 2.6 + 2.7 = 5.3 by dividing the interval [5, 6] into 10 parts of equal length 0.1. Then, the point 5.3 is located exactly at the point between the third and fourth parts.