Engage NY Eureka Math Algebra 2 Module 1 Lesson 33 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 33 Example Answer Key
Example: Finding an Analytic Equation for a Parabola
Given a focus and a directrix, create an equation for a parabola.
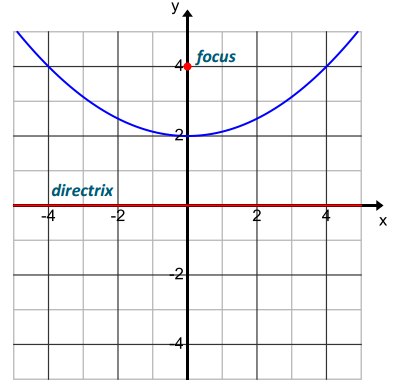
Focus: F(0, 2)
Directrix: x-axis
Parabola:
P = {((x, y) | (x,y) is equidistant from F and the x-axis.}
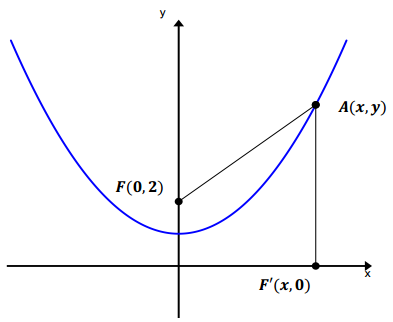
Let A be any point (x,y) on the parabola P. Let F’ be a point on the directrix with the same x-coordinate as point A.
What is the length AF’?
Answer:
AF’ = y
Use the distance formula to create an expression that represents the length AF.
Answer:
AF = \(\sqrt{(x-0)^{2}+(y-2)^{2}}\)
Create an equation that relates the two lengths, and solve it for y.
Answer:
Therefore, P = {(x, y) | \(\sqrt{(x-0)^{2}+(y-2)^{2}}\) = y}.
The two segments have equal lengths. AF’ = AF
The length of each segment y = \(\sqrt{(x-0)^{2}+(y-2)^{2}}\)
Square both sides of the equation. y2 = x2 + (y – 2)2
Expand the binomial. y2 = x2 + y2 – 4y + 4
Solve for y. 4y = x2 + 4
y = \(\frac{1}{4}\)x2 + 1
Replacing this equation in the definition of P = {(x, y) | (x, y) is equidistant from F and the x-axis) gives the statement P = {(x, y) | y = \(\frac{1}{4}\) x2 + 1}.
Thus, the parabola P is the graph of the equation y = \(\frac{1}{4}\)x2 + 1.
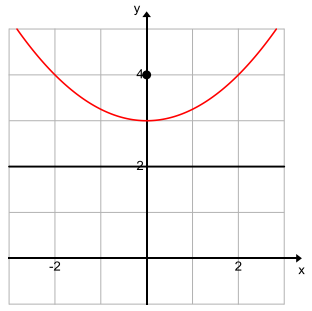
Verify that this equation appears to match the graph shown.
Answer:
Consider the point where the y-axis intersects the parabola; let this point have coordinates (0, b). From the graph, we see that 0 < b < 2. The distance from the focus (0, 2) to (0, b) is 2 – b units, and the distance from the directrix to (0, b) is b units. Since (0, b) is on the parabola, we have 2 – b = b, so that b = 1. From this perspective, we see that the point (0, 1) must be on the parabola. Does this point satisfy the equation we found? Let x = 0. Then our equation gives y = \(\frac{1}{4}\)x2 + 1 = \(\frac{1}{4}\)(0)2 + 1, so (0, 1) satisfies the equation. This is the only point that we have determined to be on the parabola at this point, but it provides evidence that the equation matches the graph.
Eureka Math Algebra 2 Module 1 Lesson 33 Opening Exercise Answer Key
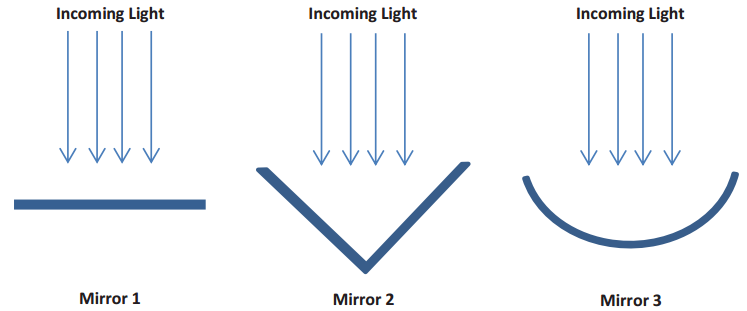
Suppose you are viewing the cross-section of a mirror. Where would the incoming light be reflected in each type of design? Sketch your ideas below.
Answer:
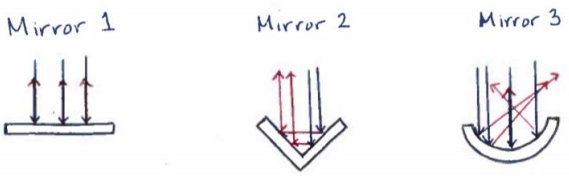
In Mirror 1, the light would reflect back onto the light rays. In Mirror 2, the light would reflect from one side of the mirror horizontally to the other side, and then reflect back upwards vertically. Incoming and outgoing rays would be parallel. In Mirror 3, the light would reflect back at different angles because the mirror is curved.
Eureka Math Algebra 2 Module 1 Lesson 33 Exercise Answer Key
Exercise 1.
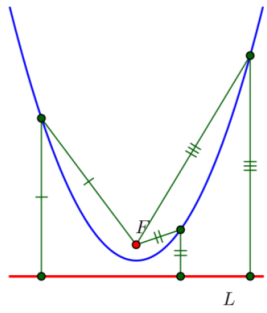
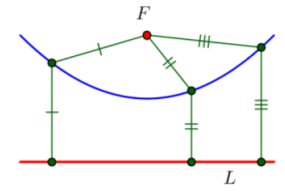
Demonstrate your understanding of the definition of a parabola by drawing several pairs of congruent segments given the parabola, its focus, and directrix. Measure the segments that you drew to confirm the accuracy of your sketches in either centimeters or inches.
Answer:
Exercise 2.
Derive the analytic equation of a parabola given the focus of (0, 4) and the directrix y = 2. Use the diagram to help you work this problem.
a. Label a point (x, y) anywhere on the parabola.
Answer:
b. Write an expression for the distance from the point (x, y) to the directrix.
Answer:
y – 2
c. Write an expression for the distance from the point (x, y) to the focus.
Answer:
\(\sqrt{(x-0)^{2}+(y-4)^{2}}\)
d. Apply the definition of a parabola to create an equation in terms of x and y. Solve this equation for y.
Answer:
y – 2 = \(\sqrt{(x-0)^{2}+(y-4)^{2}}\)
Solved for y, we find an equivalent equation is y = \(\frac{1}{4}\)x2 + 3.
e. What is the translation that takes the graph of this parabola to the graph of the equation derived in Example 1?
Answer:
A translation down two units will take this graph of this parabola to the one derived in Example 1.
Eureka Math Algebra 2 Module 1 Lesson 33 Problem Set Answer Key
Question 1.
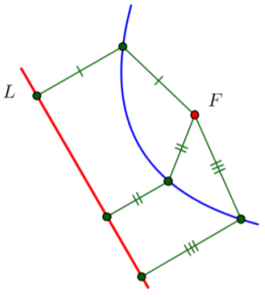
Demonstrate your understanding of the definition of a parabola by drawing several pairs of congruent segments given each parabola, its focus, and directrix. Measure the segments that you drew in either inches or centimeters to confirm the accuracy of your sketches.
Answer:
Measurements will depend on the location of the segments and the size of the printed document. Segments that should be congruent should be close to the same length.
a.
Answer:
b.
Answer:
c.
Answer:
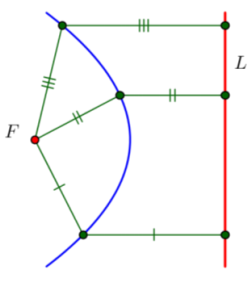
d.
Answer:
Question 2.
Find the distance from the point (4, 2) to the point (0, 1).
Answer:
The distance is √17 units.
Question 3.
Find the distance from the point (4, 2) to the line y = – 2.
Answer:
The distance is 4 units.
Question 4.
Find the distance from the point (- 1, 3) to the point (3, – 4).
Answer:
The distance is √65 units.
Question 5.
Find the distance from the point (- 1, 3) to the line y = 5.
Answer:
The distance is 2 units.
Question 6.
Find the distance from the point (x, 4) to the line y = – 1.
Answer:
The distance is 5 units.
Question 7.
Find the distance from the point (x, – 3) to the line y = 2.
Answer:
The distance is 5 units.
Question 8.
Find the values of x for which the point (x, 4) is equidistant from (0, 1), and the line y = – 1.
Answer:
If \(\sqrt{(x-0)^{2}+(4-1)^{2}}\) = 5, then x = 4 or x =- 4.
Question 9.
Find the values of x for which the point (x, – 3) is equidistant from (1, – 2), and the line y = 2.
Answer:
If \(\sqrt{(x-1)^{2}+(-3-(-2))^{2}}\) = 5, then x = 1 + 2√6 or x = 1 – 2√6
Question 10.
Consider the equation y = x2.
a. Find the coordinates of the three points on the graph of y = x2 whose x-values are 1, 2, and 3.
Answer:
The coordinates are (1, 1), (2, 4), and (3, 9).
b. Show that each of the three points in part (a) is equidistant from the point (o, \(\frac{1}{4}\)), and the line y = –\(\frac{1}{4}\).
Answer:

c. Show that if the point with coordinates (x, y) is equidistant from the point (0, \(\frac{1}{4}\)), and the line y = –\(\frac{1}{4}\) then y = x2.
Answer:
The distance from (x, y) to (o, \(\frac{1}{4}\)) is \(\sqrt{(x-0)^{2}+\left(y-\frac{1}{4}\right)^{2}}\) and the distance from (x, y) to the line y = –\(\frac{1}{4}\) is y – (-\(\frac{1}{4}\)) = y + \(\frac{1}{4}\). Setting these distances equal gives
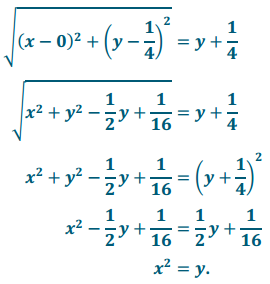
Thus, if a point (x, y) is the same distance from the point (0, \(\frac{1}{4}\)), and the line y = –\(\frac{1}{4}\), then (x, y) lies on the parabola y = x2.
Question 11.
Consider the equation y = \(\frac{1}{2}\)x2 – 2x.
a. Find the coordinates of the three points on the graph of y = \(\frac{1}{2}\)x2 – 2x whose x-values are – 2, 0, and 4.
Answer:
The coordinates are (- 2, 6), (0, 0), (4, 0).
b. Show that each of the three points in part (a) is equidistant from the point (2, –\(\frac{3}{2}\)) and the line y = –\(\frac{5}{2}\).
Answer:
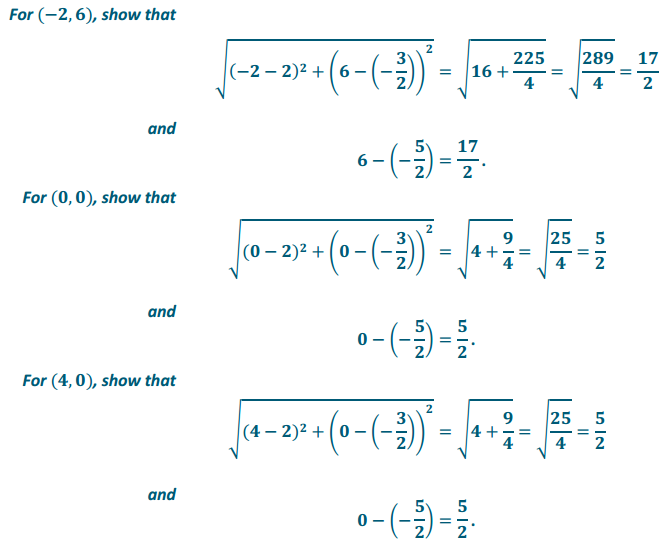
c. Show that if the point with coordinates (x, y) is equidistant from the point (2, –\(\frac{3}{2}\)), and the line y = –\(\frac{5}{2}\) then y = \(\frac{1}{2}\)x2 – 2x.
Answer:
The distance from (x, y) to (2, –\(\frac{3}{2}\)) is \(\sqrt{(x-2)^{2}+\left(y+\frac{3}{2}\right)^{2}}\) and the distance from (x, y) to the line y = –\(\frac{5}{2}\) is y – (-\(\frac{5}{2}\)) = y + \(\frac{5}{2}\). Setting these distances equal gives
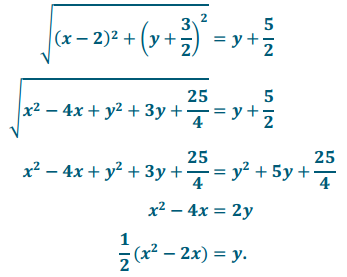
Question 12.
Derive the analytic equation of a parabola with focus (1, 3) and directrix y = 1. Use the diagram to help you work this problem.
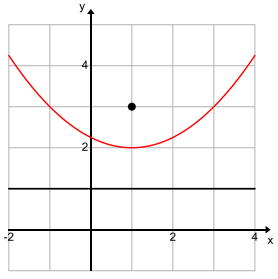
a. Label a point (x, y) anywhere on the parabola.
Answer:
b. Write an expression for the distance from the point (x, y) to the directrix.
Answer:
y – 1
c. Write an expression for the distance from the point (x, y) to the focus (1, 3).
Answer:
\(\sqrt{(x-1)^{2}+(y-3)^{2}}\)
d. Apply the definition of a parabola to create an equation in terms of x and y. Solve this equation for y.
Answer:
y – 1 = \(\sqrt{(x-1)^{2}+(y-3)^{2}}\)
(y – 1)2 =(x – 1)2 + (y – 3)2
y2 – 2y + 1 = (x – 1)2 + y2 – 6y + 9
4y = (x – 1)2 + 8
y = \(\frac{1}{4}\)(x – 1)2 + 2
y = \(\frac{1}{4}\)x2 – \(\frac{1}{2}\)x + \(\frac{9}{4}\)
e. Describe a sequence of transformations that would take this parabola to the parabola with equation y = \(\frac{1}{4}\)x2 + 1 derived In Example 1.
Answer:
A translation 1 unit to the left and 1 unit downward will take this parabola to the one derived in Example 1.
Question 13.
Consider a parabola with focus (0, – 2) and directrix on the x-axis.
a. Derive the analytic equation for this parabola.
Answer:
y = –\(\frac{1}{4}\)x2 – 1
b. Describe a sequence of transformations that would take the parabola with equation y = \(\frac{1}{4}\)x2 + 1 derived in Example 1 to the graph of the parabola in part (a).
Answer:
Reflect the graph in Example 1 across the x-axis to obtain this parabola.
Question 14.
Derive the analytic equation of a parabola with focus (0, 10) and directrix on the x-axis.
Answer:
y = \(\frac{1}{20}\)x2 + 5
Eureka Math Algebra 2 Module 1 Lesson 33 Exit Ticket Answer Key
Question 1.
Derive an analytic equation for a parabola whose focus is (0, 4) and directrix Is the x-axis. Explain how you got your answer.
Answer:
Let (x, y) be a point on the parabola. Then, the distance between this point and the focus is given by
\(\sqrt{(x-0)^{2}+(y-4)^{2}}\). The distance between the point (x, y) and the directrix is y. Then,
y = \(\sqrt{(x-0)^{2}+(y-4)^{2}}\)
y2 = x2 + y2 – 8y + 16
8y = x2 + 16
y = \(\frac{1}{8}\)x2 + 2
Question 2.
Sketch the parabola from Question 1. Label the focus and directrix.
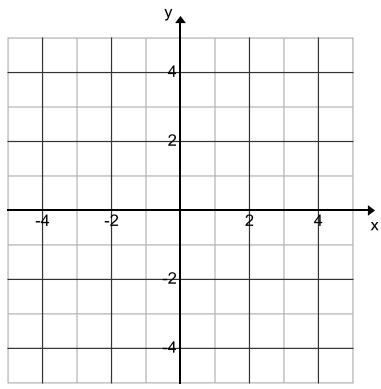
Answer: