Engage NY Eureka Math Algebra 2 Module 1 Lesson 31 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 31 Exercise Answer Key
Exercise 1.
Draw a graph of the circle with equation x2 + y2 = 9.
a. What are the solutions to the system of circle and line when the circle is given by x2 + y2 = 9, and the line is given by y = 2?
Answer:
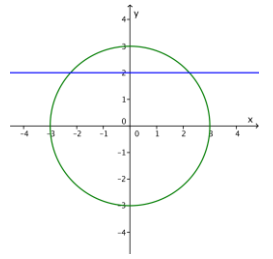
Substituting y = 2 in the equation of the circle yields x2 + 4 = 9, so x2 = 5, and x = √5 or x = -√5. The solutions are (-√5, 2) and (√5, 2).
b. What happens when the line is given by y = 3?
Answer:
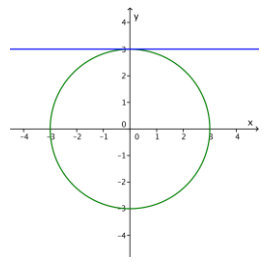
Substituting y = 3 in the equation of the circle yields x2 + 9 = 9, so x2 = 0. The line is tangent to the circle, and the solution is (0, 3).
c. What happens when the line is given by y = 4?
Answer:

Substituting y = 4 in the equation of the circle yields x2 + 16 = 9, so x2 = – 7. Since there are no real numbers that satisfy x2 = – 7, there is no solution to this equation. This indicates that the line and circle do not intersect.
Exercise 2.
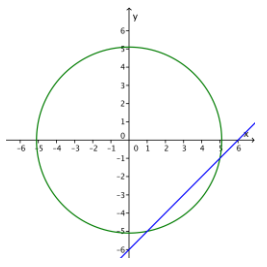
By solving the equations as a system, find the points common to the line with equation x – y = 6 and the circle with equation x2 + y2 = 26. Graph the line and the circle to show those points.
Answer:
(5, – 1) and (1, – 5). See picture to the right.
Exercise 3.
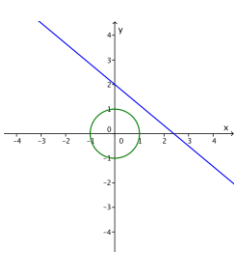
Graph the line given by 5x + 6y = 12 and the circle given by x2 + y2 = 1. Find all solutions to the system of equations.
Answer:
There is no real solution; the line and circle do not intersect. See picture to the right.
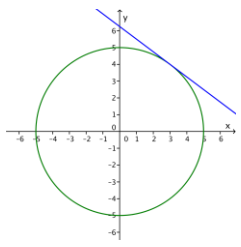
Exercise 4.
Graph the line given by 3x + 4y = 25 and the circle given by x2 + y2 = 25. Find all solutions to the system of equations. Verify your result both algebraically and graphically.
Answer:
The line is tangent to the circle at (3, 4), which is the only solution. See picture to the right.
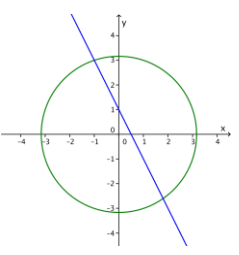
Exercise 5.
Graph the line given by 2x + y = 1 and the circle given by x2 + y2 = 10. Find all solutions to the system of equations. Verify your result both algebraically and graphically.
Answer:
The line and circle intersect at (- 1, 3) and \(\left(\frac{9}{5},-\frac{13}{5}\right)\), which are the two solutions. See picture to the right.
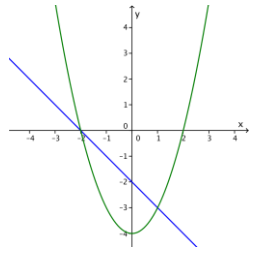
Exercise 6.
Graph the line given by x + y = – 2 and the quadratic curve given by y = x2 – 4. Find all solutions to the system of equations. Verify your result both algebraically and graphically.
Answer:
The line and the parabola intersect at (1, – 3) and (- 2, 0), which are the two solutions. See picture to ‘ the right.
Eureka Math Algebra 2 Module 1 Lesson 31 Problem Set Answer Key
Question 1.
Where do the lines given by y = x + b and y = 2x + 1 intersect?
Answer:
Since we do not know the value of b, we cannot solve this problem by graphing, and we will have to approach it algebraically. Eliminating y gives the equation
x + b = 2x + 1
x = b – 1.
Since x = b – 1, we have y = x + b = (b – 1) + b = 2b – 1. Thus, the lines intersect at the point (b – 1, 2b – 1).
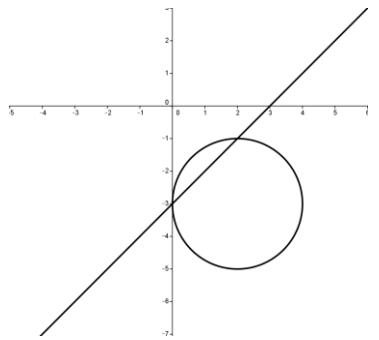
Question 2.
Find all solutions to the following system of equations.
(x – 2)2 + (y + 3)2 = 4
x – y = 3
Illustrate with a graph.
Answer:
Solve the linear equation for one of the variables: x = y + 3.
Substitute that variable in the quadratic equation:
(y + 3 – 2)2 + (y + 3)2 = 4.
Rewrite the equation in standard form: 2y2 + 8y + 6 = 0.
Solve the quadratic equation: 2(y + 3)(y + 1) = 0, so
y = – 3 or y = -1.
If y = – 3, then x = 0. If y = -1, then x = 2.
As the graph shows, the solution is the two points (0, -3) and (2, -1).
Question 3.
Find all solutions to the following system of equations.
x + 2y = 0
x2 – 2x + y2 – 2y – 3 = 0
Illustrate with a graph.
Answer:
Solve the linear equation for one of the variables: x = – 2y.
Substitute that variable in the quadratic equation:
(-2y)2 – 2(-2y) + y2 – 2y – 3 = 0.
Rewrite the equation in standard form: 5y2 + 2y – 3 = 0.
Solve the quadratic equation: (5y – 3)(y + 1) = 0, so y = \(\frac{3}{5}\) or
y = – 1.
If y = \(\frac{3}{5}\), then x = –\(\frac{6}{5}\). If y = – 1, then x = 2.
As the graph shows, the solutions are the two points: (-\(\frac{6}{5}\), \(\frac{3}{5}\)) and (2, -1).
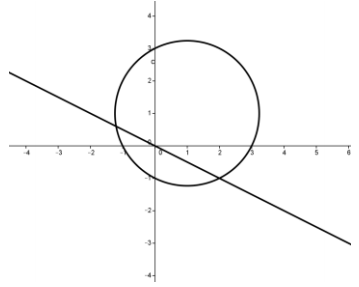
Question 4.
Find all solutions to the following system of equations.
x + y = 4
(x + 3)2 + (y – 2)2 = 10
Illustrate with a graph.
Answer:
Solve the linear equation for one of the variables: x = 4 – y.
Substitute that variable in the quadratic equation:
(4 – y + 3)2 + (y – 2)2 = 10.
Rewrite the equation in standard form: 2y2 – 18y + 43 = 0.
Solve the equation using the quadratic formula:
y = \(\frac{18+\sqrt{324-344}}{4}\) or y = \(\frac{18-\sqrt{324-344}}{4}\)
So we have y = \(\frac{1}{2}\)(9 + √-5) or y = \(\frac{1}{2}\)(9 – √-5).
Therefore, there is no real solution to the system.
As the graph shows, the line and circle do not intersect.
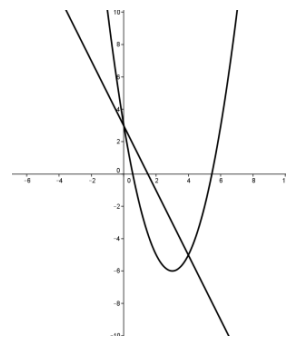
Question 5.
Find all solutions to the following system of equations.
y = – 2x + 3
y = x2 – 6x + 3
Illustrate with a graph.
Answer:
The linear equation is already solved for one of the variables: y = -2x + 3.
Substitute that variable in the quadratic equation: – 2x + 3 = x2 – 6x + 3.
Rewrite the equation in standard form: x2 – 4x = 0.
Solve the quadratic equation: x(x – 4) = 0.
So, x = 0 or x = 4.
If x = 0, then y = 3. If x = 4, then y = – 5.
As the graph shows, the solutions are the two points (0, 3) and (4, – 5).
Question 6.
Find all solutions to the following system of equations.
– y2 + 6y + x – 9 = 0
6y = x + 27
Illustrate with a graph.
Answer:
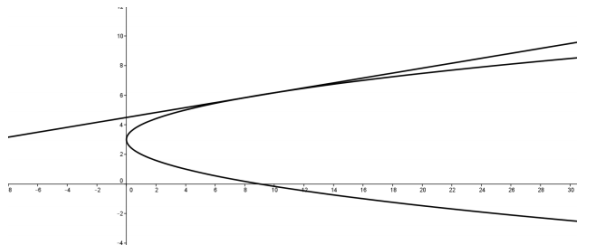
Solve the second equation for x: x = 6y – 27.
Substitute in the first equation: – y2 + 6y + 6y – 27 – 9 = 0.
Combine like terms: – y2 + 12y – 36 = 0.
Rewrite the equation in standard form and factor: – (y – 6)2 = 0.
Therefore, y = 6. Then x = 6y – 27, so x = 9.
There is only one solution (9, 6), and as the graph shows, the line is tangent to the parabola.
An alternative solution would be to solve the linear equation for y instead of x, getting the quadratic equation (x – 9)(x – 9) = 0, which gives the repeated root x = 9 and the same point of tangency (9, 6).
Another alternative solution would be to solve the quadratic equation for x, so that x = y2 – 6y + 9. Substituting in the linear equation would yield 6y = y2 – 6y + 9 + 27. Converting that to standard form would give y2 – 12y + 36 = 0, which gives the repeated root y = 6, as in the first solution. Note that in this case, unlike when the graph of the quadratic equation is a circle, the quadratic equation can be solved for x in terms of y without getting a radical expression.
Question 7.
Find all values of k so that the following system has two solutions.
x2 + y2 = 25
y = k
Illustrate with a graph.
Answer:
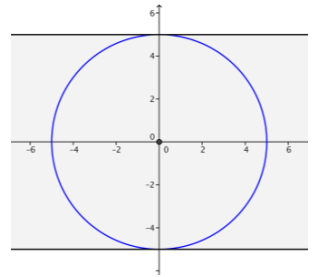
The center of the circle is the origin, and the line is parallel to the x-axis. Therefore, as the graph shows, there are two solutions only when – 5 < k < 5.
Question 8.
Find all values of k so that the following system has exactly one solution.
y = 5 – (x – 3)2
y = k
Illustrate with a graph.
Answer:
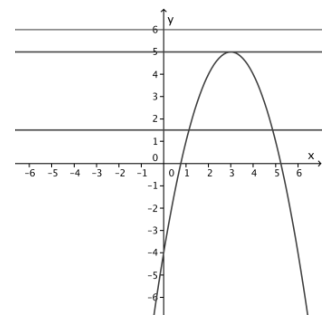
The parabola opens down, and its axis of symmetry is the vertical line x = 3. The line y = k is a horizontal line and will intersect the parabola in either two, one, or no points. It intersects the parabola in one point only if it passes through the vertex of the parabola, which is k = 5.
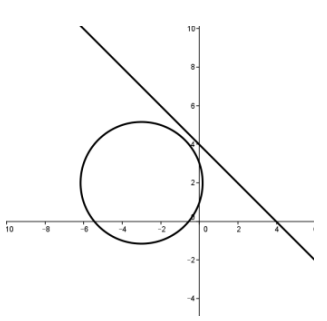
Question 9.
Find all values of k so that the following system has no solutions.
x2 + (y – k)2 = 36
y = 5x + k
Illustrate with a graph.
Answer:
The circle has radius 6 and center (0, k). The line has slope 5 and crosses the y-axis at (0, k). Since for any value of k the line passes through the center of the circle, the line intersects the circle twice. (In the figure on the left below, k = 2, and in the one on the right below, k = – 3.) There is no value of k for which there is no solution.
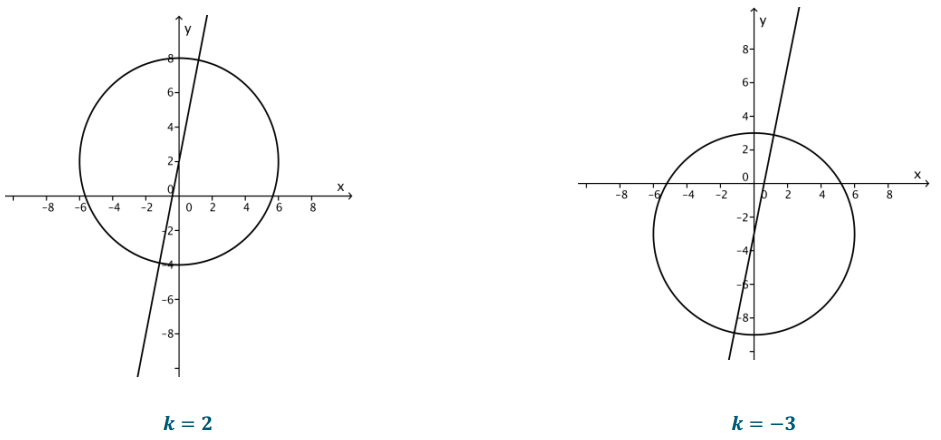
Eureka Math Algebra 2 Module 1 Lesson 31 Exit Ticket Answer Key
Make and explain a prediction about the nature of the solution to the following system of equations, and then solve the system.
x2 + y2 = 25
4x + 3y = 0
Illustrate with a graph. Verify your solution, and compare it with your initial prediction.
Answer:

Prediction: By inspecting the equations, students should conclude that the circle is centered at the origin, and that the line goes through the origin. So, the solution should consist of two points.
Solution: Solve the linear equation for one of the variables: y = – \(\frac{4 x}{3}\)
Substitute that variable in the quadratic equation: x2 + \(\left(-\frac{4 x}{3}\right)^{2}\) = 25.
Remove parentheses and combine like terms: 25x2 – 25 ∙ 9 = 0,
so x2 – 9 = 0.
Solve the quadratic equation in x: (x + 3)(x – 3) = 0, which gives the roots 3 and – 3.
Substitute into the linear equation: If x = 3, then y = – 4; if x = – 3, then y = 4.
As the graph shows, the solution is the two points of intersection of the circle and the line: (3, – 4) and (- 3, 4).
An alternative solution would be to solve the linear equation for x instead of y, getting the quadratic equation (y + 4)(y – 4) = 0, which gives the roots 4 and – 4 and the same points of intersection.
Eureka Math Algebra 2 Module 1 Lesson 31 Exploratory Challenge Answer Key
Exploratory Challenge 1
a. Sketch the lines given by x + y = 6 and – 3x + y = 2 on the same set of axes to solve the system graphically. Then solve the system of equations algebraically to verify your graphical solution.
Answer:
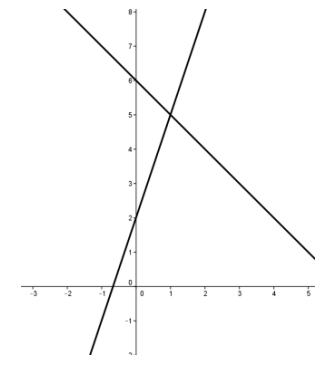
The point (1, 5) should be easily identifiable from the sketch. See the graph to the right.
Solving each equation for y gives the system
y = – x + 6
y = 3x + 2.
This leads to the single-variable equation
– x + 6 = 3x + 2
4x = 4
x = 1
y = – 1 + 6
y = 5.
Thus, the solution is the point (1, 5).
b. Suppose the second line is replaced by the line with equation x + y = 2. Plot the two lines on the same set of axes, and solve the pair of equations algebraically to verify your graphical solution.
Answer:
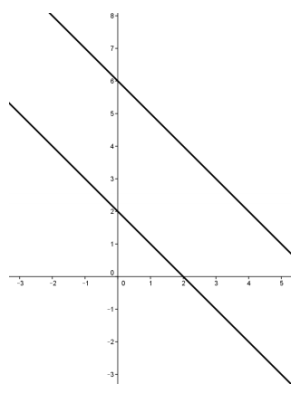
The lines are parallel, and there is no point in common. See the graph to the right.
If we try to solve the system algebraically, we have
y = – x + 6
y = – x + 2,
which leads to the single-variable equation
– x + 6 = – x + 2
4 = 0.
Since 4 = 0 is not a true number sentence, the system has no solution.
c. Suppose the second line ¡s replaced by the line with equation 2x = 12 – 2y. Plot the lines on the same set of axes, and solve the pair of equations algebraically to verify your graphical solution.
Answer:
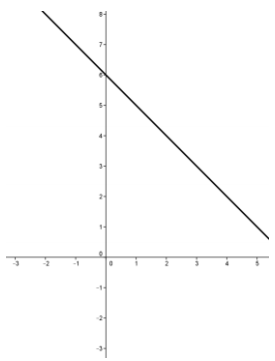
The lines coincide, and they have all points in common. See the graph to the right.
Algebraically, we have the system
y = – x + 6
y = – x + 6,
which leads to the equation
– x + 6 = – x + 6
0 = 0.
Thus all points (x, – x + 6) are solutions to the system.
d. We have seen that a pair of lines can intersect in 1, 0, or an infinite number of points. Are there any other possibilities?
Answer:
No. Students should convince themselves and each other that these three options exhaust the possibilities for the intersection of two lines.
Exploratory Challenge 2
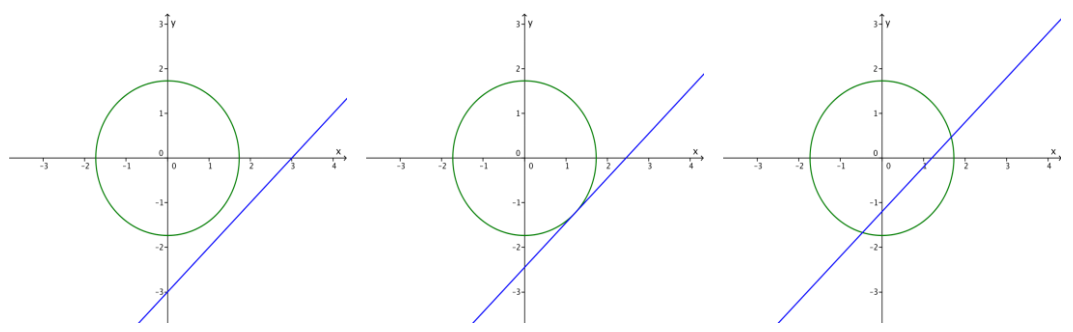
a. Suppose that instead of equations for a pair of lines, you were given an equation for a circle and an equation for a line. What possibilities are there for the two figures to intersect? Sketch a graph for each possibility.
Answer:
They can intersect in 0, 1, or 2 points as shown below.
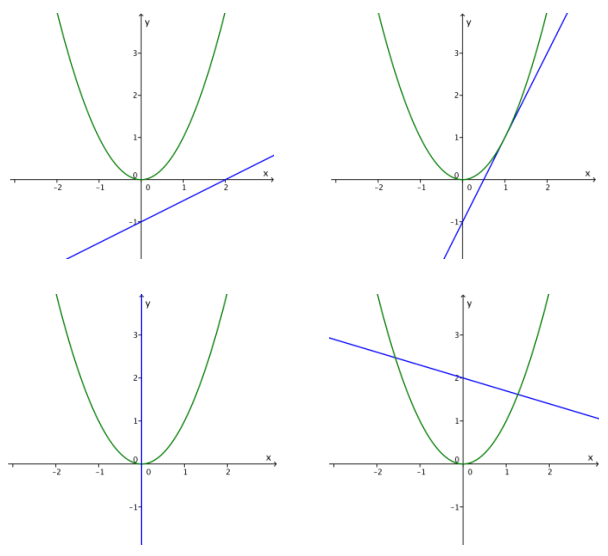
b. Graph the parabola with equation y = x2. What possibilities are there for a line to intersect the parabola? Sketch each possibility.
Answer:
The parabola and line can intersect in 0, 1, or 2 points as shown below. Note that, in contrast to the circle, where all the lines intersecting the circle in one point are tangent to it, lines intersecting the parabola in one point are either tangent to it or are parallel to the parabola’s axis of symmetry in this case, the y-axis.
c. Sketch the circle given by x2 + y2 = 1 and the line given by y = 2x + 2 on the same set of axes. One solution to the pair of equations is easily identifiable from the sketch. What is it?
Answer:
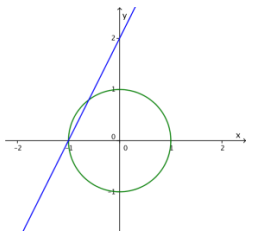
The point (- 1, 0) should be easily identifiable from the sketch, but the other point is not.
d. Substitute y = 2x + 2 into the equation x2 + y2 = 1, and solve the resulting equation for x.
Answer:
Factoring or using the quadratic formula, students should find that the solutions to x2 + (2x + 2)2 = 1 are – 1 and –\(\frac{3}{5}\).
e. What does your answer to part (d) tell you about the intersections of the circle and the line from part (c)?
Answer:
There are two intersections of the line and the circle. When x = – 1, then y = 0, as the sketch shows, so (- 1, 0) is a solution. When x = – \(\frac{3}{5}\), then y = 2 (-\(\frac{3}{5}\)) + 2 = \(\frac{4}{5}\), so \(\left(-\frac{3}{5}, \frac{4}{5}\right)\) is another solution.