Eureka Math Algebra 2 Module 1 Lesson 30 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 30 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 30 Example Answer Key

Example 1.
Determine the values for x, y, and z in the following system:
2x + 3y – z = 5
4x – y – z = – 1
x + 4y + z = 12
Answer:
2x + 3y – z = 5 …….. (1)
4x – y – z = – 1 …….. (2)
x + 4y + z = 12 …….. (3)
Suggest numbering the equations as shown above to help organize the process.
→ Eliminate z from equations (1) and (2) by subtraction. Replace equation (1) with the result.

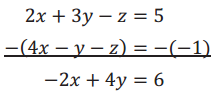
→ Our goal is to find two equations in two unknowns. Thus, we will also eliminate z from equations (2) and (3) by adding as follows. Replace equation (3) with the result.

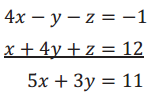
→ Our new system of three equations in three variables has two equations with only two variables in them:
– 2x + 4y = 6
4x – y – z = -1
5x + 3y = 11.

→ These two equations now give us a system of two equations in two variables, which we reviewed how to solve in Exercises 1 – 2.
– 2x + 4y = 6
5x + 3y = 11
At this point, let students solve this individually or with partners, or guide them through the process if necessary.

→ To get matching coefficients, we need to multiply both equations by a constant:
5(- 2x + 4y) = 5(6)     →      – 10x + 20y = 30
2(5x + 3y) = 2(11)     →     10x + 6y = 22.

→ Replacing the top equation with the sum of the top and bottom equations together gives the following:
26y = 52
10x + 6y = 22.

→ Replace y = 2 in one of the equations to find x:
5x + 3(2) = 11
5x + 6 = 11
5x = 5
x = 1.

→ Replace x = 1 and y = 2 in any of the original equations to find z:
2(1) + 3(2) – z = 5
2 + 6 – z = 5
8 – z = 5
z = 3.
→ The solution, x = 1, y = 2, and z = 3, can be written compactly as an ordered triple of numbers (1, 2, 3).

Consider pointing out to students that the point (1, 2, 3) can be thought of as a point in a three-dimensional coordinate plane, and that it is, like a two-by-two system of equations, the intersection point in three-space of the three planes given by the graphs of each equation. These concepts are not the point of this lesson, so addressing them is optional.

Point out that a linear system involving three variables requires three equations in order for the solution to possibly be a single point.

The following problems provide examples of situations that require solving systems of equations in three variables.

Eureka Math Algebra 2 Module 1 Lesson 30 Exercise Answer Key

Determine the value of x and y in the following systems of equations.

Exercise 1.
2x + 3y = 7
2x + y = 3
Answer:
x = \(\frac{1}{2}\), y = 2

Exercise 2.
5x – 2y = 4
Answer:
– 2x + y = 2
x = 8, y = 18

Exercise 3.
A scientist wants to create 120 ml of a solution that is 30% acidic. To create this solution, she has access to a 20% solution and a 45% solution. How many milliliters of each solution should she combine to create the 30% solution?
Answer:
Milliliters of 20% solution: x ml
Milliliters of 45% solution: y ml
Write one equation to represent the total amounts of each solution needed:
x + y = 120.
Since 30% of 120 ml is 36, we can write one equation to model the acidic portion:
0.20x + 0.45y = 36.
Writing these two equations as a system:
x + y = 120
0.20x + 0.45y = 36

To solve, multiply both sides of the top equation by either 0.20 to eliminate x or 0.45 to eliminate y. The following steps will eliminate x:
0. 20(x + y) = 0.20(120)
0.20x + 0.45y = 40
which gives
0.20x + 0.20y = 24
0.20x + 0.45y = 36.

Replacing the top equation with the difference between the bottom equation and top equation results in a new system with the same solutions:
0.25y = 12
0.20x + 0.45y = 36.
The top equation can quickly be solved for y,
y = 48,
and substituting y = 48 back into the original first equation allows us to find x:
x + 48 = 120
x = 72.
Thus, we need 48 ml of the 45% solution and 72 ml of the 20% solution.

Exercise 4.
Given the system below, determine the values of r, s, and u that satisfy all three equations.
r + 2s – u = 8
s + u = 4
r – s – u = 2
Answer:
Adding the second and third equations together produces the equation r = 6. Substituting this into the first equation and adding it to the second gives 6 + 3s = 12, so that s = 2. Replacing s with 2 in the second equation gives u = 2. The solution to this system of equations is (6, 2, 2).

Exercise 5.
Find the equation of the form y = ax² + bx + c whose graph passes through the points (1, 6), (3, 20), and (- 2, 15).
Answer:
We find a = 2, b = – 1, c = 5; therefore, the quadratic equation is y = 2x² – x + 5.

→ Since we know three ordered pairs, we can create three equations.
6 = a + b + c
20 = 9a + 3b + c
15 = 4a – 2b + c
Ask students to explain where the three equations came from. Then have them use the technique from Example 1 to solve this system.

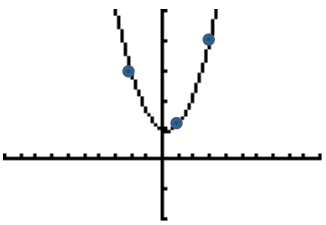
Have students use a graphing utility to plot y = 2x² – x + 5 along with the original three points to confirm their answer.

Eureka Math Algebra 2 Module 1 Lesson 30 Problem Set Answer Key

Solve the following systems of equations.

Question 1.
x + y = 3
y + z = 6
x + z = 5
Answer:
x = 1, y = 2, z = 4 or (1, 2, 4)

Question 2.
r = 2(s – t)
2t = 3(s – r)
r + t = 2s – 3
Answer:
r = 2, s = 4, t = 3, or (2, 4, 3)

Question 3.
2a + 4b + c = 5
a – 4b = – 6
2b + c = 7
Answer:
a = – 2, b = 1, c = 5 or (- 2, 1, 5)

Question 4.
2x + y – z = – 5
4x – 2y + z = 10
2x + 3y + 2z = 3
x = \(\frac{1}{2}\), y = – 2, z = 4 or (\(\frac{1}{2}\), – 2, 4)

Question 5.
r + 3s + t = 3
2r – 3s + 2t = 3
– r + 3s – 3t = 1
r = 3, s = \(\frac{1}{3}\), t = -1 or (3, \(\frac{1}{3}\), -1)

Question 6.
x – y = 1
2y + z = – 4
x – 2z = – 6
Answer:
x = – 2, y = -3, z = 2 or (- 2, – 3,2)

Question 7.
x = 3(y – z)
y = 5(z – x)
x + y = z + 4
Answer:
x = 3, y = 5, z = 4 or (3, 5, 4)

Question 8.
p + q + 3r = 4
2q + 3r = 7
p – q – r = – 2
Answer:
p = 2, q = 5, r = – 1 or (2, 5, – 1)

Question 9.
\(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\) = 5
\(\frac{1}{x}+\frac{1}{y}\) = 2
\(\frac{1}{x}-\frac{1}{y}\) = – 2
Answer:
x = 1, y = 1, z = \(\frac{1}{3}\) or (1, 1, \(\frac{1}{3}\))

Question 10.
\(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\) = 6
\(\frac{1}{b}+\frac{1}{c}\) = 5
\(\frac{1}{a}-\frac{1}{b}\) = – 1
Answer:
a = -1, b = \(\frac{1}{2}\), c = \(\frac{1}{3}\) or (1, \(\frac{1}{2}\), \(\frac{1}{3}\))

Question 11.
Find the equation of the form y = ax² + bx + c whose graph passes through the points (1, – 1), (3, 23), and (- 1, 7).
Answer:
y = 4x² – 4x – 1

Question 12.
Show that for any number t, the values x = t + 2, y = 1 – t, and z = t + 1 are solutions to the system of equations below.
x + y = 3
y + z = 2
(In this situation, we say that t parameterizes the solution set of the system.)
Answer:
x + y = (t + 2) + (1 – t) = 3
y + z = (1 – t) + (t + 1) = 2

Question 13.
Some rational expressions can be written as the sum of two or more rational expressions whose denominators are the factors of its denominator (called a partial fraction decomposition). Find the partial fraction decomposition for \(\frac{1}{n(n+1)}\) by finding the value of A that makes the equation below true for all n except 0 and – 1.

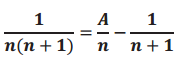
Answer:
Adding \(\frac{1}{n+1}\) to both sides of the equations, we have

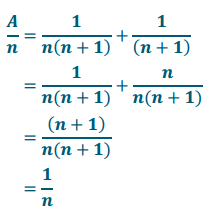
so A = 1 and thus \(\frac{1}{n(n+1)}=\frac{1}{n}-\frac{1}{n+1}\).

Question 14.
A chemist needs to make 40 ml of a 15% acid solution. He has a 5% acid solution and a 30% acid solution on hand. If he uses the 5% and 30% solutions to create the 15% solution, how many ml of each does he need?
Answer:
He needs 24 ml of the 5% solution and 16 ml of the 30% solution.

Question 15.
An airplane makes a 400-mile trip against a head wind in 4 hours. The return trip takes 2. 5 hours, the wind now being a tail wind. If the plane maintains a constant speed with respect to still air, and the speed of the wind is also constant and does not vary, find the still-air speed of the plane and the speed of the wind.
Answer:
The speed of the plane in still wind is 130 mph, and the speed of the wind is 30 mph.

Question 16.
A restaurant owner estimates that she needs the same number of pennies as nickels and the same number of dimes as pennies and nickels together. How should she divide $26 between pennies, nickels, and dimes?
Answer:
She will need 200 dimes ($20 worth), 100 nickels ($5 worth), and 100 pennies ($1 worth) for a total of $26.

Eureka Math Algebra 2 Module 1 Lesson 30 Exit Ticket Answer Key

For the following system, determine the values of p, q, and r that satisfy all three equations:
2p + q – r = 8
q + r = 4
p – q = 2.
Answer:
p = 4, q = 2, r = 2, or equivalently (4, 2, 2)