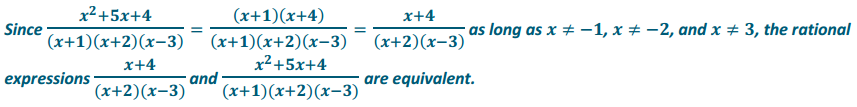Engage NY Eureka Math Algebra 2 Module 1 Lesson 22 Answer Key
Eureka Math Algebra 2 Module 1 Lesson 22 Example Answer Key
Consider the following rational expression: \(\frac{2(a-1)-2}{6(a-1)-3 a}\). Turn to your neighbor, and discuss the following: For what values of a is the expression undefined?
Answer:
Sample students’ answers. When they suggest that the denominator cannot be zero, give the class a minute to work out that the denominator is zero when a = 2.
\(\frac{2(a-1)-2}{6(a-1)-3 a}\)
6(a – 1) – 3a = 0
6a – 6 – 3a = 0
3a – 6 = 0
a = 2
→ Let’s reduce the rational expression with \(\frac{2(a-1)-2}{6(a-1)-3 a}\) to lowest terms. Since no common factor is visible in the given form of the expression, we first simplify the numerator and denominator by distributing and combining like terms.
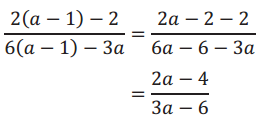
→ Next, we factor the numerator and denominator, and divide both by any common factors. This step shows clearly why we had to specify that a ≠ 2.
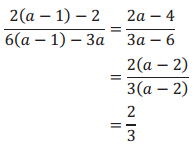
→ As long as a ≠ 2, we see that \(\frac{2(a-1)-2}{6(a-1)-3 a}\) and \(\frac{2}{3}\) are equivalent rational expressions.
If we allow a to take on the value of 2, then \(\frac{2(a-1)-2}{6(a-1)-3 a}\) is undefined. However, the expression \(\frac{2}{3}\) is always defined, so these expressions are not equivalent.
Eureka Math Algebra 2 Module 1 Lesson 22 Opening Exercise Answer Key
On your own or with a partner, write two fractions that are equivalent to \(\frac{1}{3}\) and use the slips of paper to create visual models to justify your response.
Answer:
Use the following to either walk through the exercise for scaffolding or as an example of likely student responses.
→ We can use the following area model to represent the fraction \(\frac{1}{3}\). Because the three boxes have the same area, shading one of the three boxes shows that \(\frac{1}{3}\) of the area in the figure is shaded.
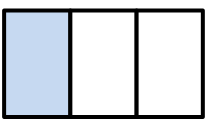
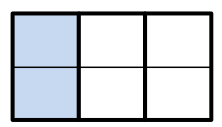
→ Now, if we draw a horizontal line dividing the columns in half, we have six congruent rectangles, two of which are shaded so that \(\frac{2}{6}\) of the area in the figure
is shaded.
→ In the figure below, we have now divided the original rectangle into nine congruent sub-rectangles, three of which are shaded so that \(\frac{3}{9}\) of the area in the figure is shaded.
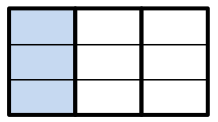
→ Let’s suppose that the area of the original rectangle is 1. In walking the class through the example, point out that the shaded area in the first figure is \(\frac{1}{3}\), the shaded area in the second figure is \(\frac{2}{6}\), and the shaded area in the third figure is \(\frac{3}{9}\). Since the area of the shaded regions are the same in all three figures, we see that \(\frac{1}{3}=\frac{2}{6}=\frac{3}{9}\). Thus, \(\frac{1}{3}\), \(\frac{2}{6}\), and \(\frac{3}{9}\) are equivalent fractions.
If students come up with different equivalent fractions, then incorporate those into the discussion of equivalent areas, noting that the shaded regions are the same for every student.
→ Now, what if we were to choose any positive integer n and draw lines across our figure so that the columns are divided into n pieces of the same size? What is the area of the shaded region?
Give students time to think and write, and ask them to share their answers with a partner. Anticipate that students will express the generalization in words or suggest either \(\frac{1}{3}\) or \(\frac{n}{3n}\). Both are correct and, ideally, both will be suggested.
→ Thus, we have the rule:
If a, b, and n are integers with n ≠ 0 and b ≠ 0, then
\(\frac{n a}{n b}=\frac{a}{b}\).
The result summarized in the box above is also true for real numbers a, b, and n, as well as for polynomial and rational expressions.
→ Then \(\frac{2}{6}=\frac{2(1)}{2(3)}=\frac{1}{3}\) and \(\frac{3}{9}=\frac{3(1)}{3(3)}=\frac{1}{3}\)
→ We say that a rational number is simplified, or reduced to lowest terms, when the numerator and denominator do not have a factor in common. Thus, while \(\frac{1}{3}\), \(\frac{2}{6}\), and \(\frac{3}{9}\) are equivalent, only \(\frac{1}{3}\) is in lowest terms.
Eureka Math Algebra 2 Module 1 Lesson 22 Exercise Answer Key
Exercise 1.
Reduce the following rational expressions to lowest terms, and identify the values of the variable(s) that must be excluded to prevent division by zero.
a. \(\frac{2(x+1)+2}{(2 x+3)(x+1)-1}\)
Answer:
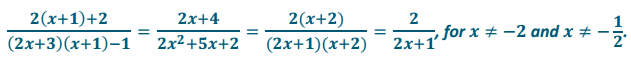
b. \(\frac{x^{2}-x-6}{5 x^{2}+10 x}\)
Answer:
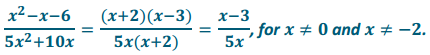
c. \(\frac{3-x}{x^{2}-9}\)
Answer:
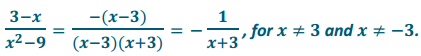
d. \(\frac{3 x-3 y}{y^{2}-2 x y+x^{2}}\)
Answer:
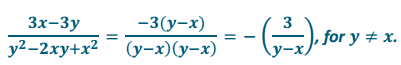
Eureka Math Algebra 2 Module 1 Lesson 22 Problem Set Answer Key
Question 1.
Find an equivalent rational expression in lowest terms, and identify the value(s) of the variable that must be excluded to prevent division by zero.
a. \(\frac{16 n}{20 n}\)
Answer:
\(\frac{4}{5}\); n ≠ 0
b. \(\frac{x^{3} y}{y^{4} x}\)
Answer:
\(\frac{x^{2}}{y^{3}}\); x ≠ 0 and y ≠ 0
c. \(\frac{2 n-8 n^{2}}{4 n}\)
Answer:
\(\frac{1-4 n}{2}\); n ≠ 0
d. \(\frac{d b+d c}{d b}\)
Answer:
\(\frac{b+c}{b}\); b ≠ 0 and d ≠ 0
e. \(\frac{x^{2}-9 b^{2}}{x^{2}-2 x b-3 b^{2}}\)
Answer:
\(\frac{x+3 b}{x+b}\); x ≠ 3b and x ≠ – b
f. \(\frac{3 n^{2}-5 n-2}{2 n-4}\)
Answer:
\(\frac{3 n+1}{2}\); n ≠ 2
g. \(\frac{3 x-2 y}{9 x^{2}-4 y^{2}}\)
Answer:
\(\frac{1}{3 x+2 y}\); y ≠ \(\frac{3}{2}\)x and y ≠ –\(\frac{3}{2}\)x
h. \(\frac{4 a^{2}-12 a b}{a^{2}-6 a b+9 b^{2}}\)
Answer:
\(\frac{4 a}{a-3 b}\); a ≠ 3b
i. \(\frac{y-x}{x-y}\)
Answer:
– 1; x ≠ y
j. \(\frac{a^{2}-b^{2}}{b+a}\)
Answer:
a – b; a ≠ – b
k. \(\frac{4 x-2 y}{3 y-6 x}\)
Answer:
\(-\frac{2}{3}\); y ≠ 2x
l. \(\frac{9-x^{2}}{(x-3)^{3}}\)
Answer:
\(-\frac{3+x}{(x-3)^{2}}\); x ≠ 3
m. \(\frac{x^{2}-5 x+6}{8-2 x-x^{2}}\)
Answer:
\(-\frac{x-3}{4+x}\); x ≠ 2 and x ≠ – 4
n. \(\frac{a-b}{x a-x b-a+b}\)
Answer:
\(\frac{1}{x-1}\); x ≠ 1 and a ≠ b
o. \(\frac{(x+y)^{2}-9 a^{2}}{2 x+2 y-6 a}\)
Answer:
\(\frac{x+y+3 a}{2}\); a ≠ \(\frac{x+y}{3}\)
p. \(\frac{8 x^{3}-y^{3}}{4 x^{2}-y^{2}}\)
Answer:
\(\frac{4 x^{2}+2 x y+y^{2}}{2 x+y}\); y ≠ 2x and y ≠ – 2x
Question 2.
Write a rational expression with denominator 6b that is equivalent to
a. \(\frac{a}{b}\)
Answer:
\(\frac{6a}{6b}\)
b. one – half of \(\frac{a}{b}\).
Answer:
\(\frac{3a}{6b}\)
c. \(\frac{1}{3}\)
Answer:
\(\frac{2b}{6b}\)
Question 3.
Remember that algebra is just a symbolic method for performing arithmetic.
a. Simplify the following rational expression: \(\frac{\left(x^{2} y\right)^{2}(x y)^{3} z^{2}}{\left(x y^{2}\right)^{2} y z}\)
Answer:
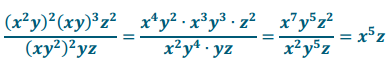
b. Simplify the following rational expression without using a calculator: \(\frac{12^{2} \cdot 6^{3} \cdot 5^{2}}{18^{2} \cdot 15}\).
Answer:
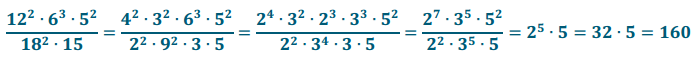
c. How are the calculations in parts (a) and (b) similar? How are they different? Which expression was easier to simplify?
Answer:
Both simplifications relied on using the rules of exponents. It was easier to simplify the algebraic expression in part (a) because we did not have to factor any numbers, such as 18, 15, and 12. However, if we substitute x = 2, y = 3, and z = 5, these two expressions have the exact same structure. Algebra allows us to do this calculation more quickly.
Eureka Math Algebra 2 Module 1 Lesson 22 Exit Ticket Answer Key
Question 1.
Find an equivalent rational expression In lowest terms, and identify the value(s) of the variables that must be excluded to prevent division by zero.
Answer:
If x ≠ 3 and x ≠ 2, then we have
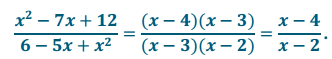
Question 2.
Determine whether or not the rational expressions \(\) and \(\) are equivalent for x ≠ – 1, x ≠ – 2, and x ≠ – 3. Explain how you know.
Answer: