Eureka Math Algebra 2 Module 1 Lesson 21 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 21 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 21 Mathematical Modeling Exercise Answer Key

The Environmental Protection Agency (EPA) is studying the flow of a river in order to establish flood zones. The EPA hired a surveying company to determine the flow rate of the river, measured as volume of water per minute. The firm set up a coordinate system and found the depths of the river at five locations as shown on the graph below. After studying the data, the firm decided to model the riverbed with a polynomial function and divide the area into six regions that are either trapezoidal or triangular so that the overall area can be easily estimated. The firm needs to approximate the depth of the river at two more data points in order to do this.

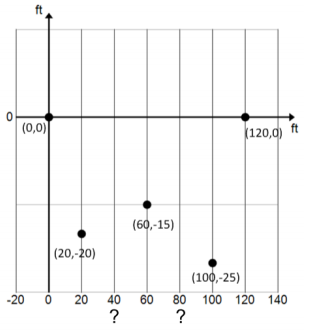
Answer:

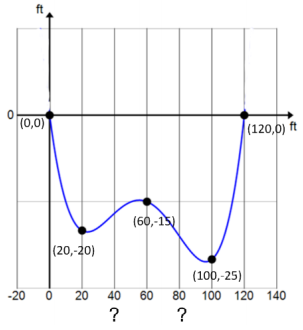
Exercise 1.
Find a polynomial P that fits the five given data points.
Answer:

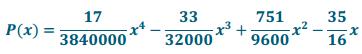
Exercise 2.
Use the polynomial to estimate the depth of the river at x = 40 and x = 80.
Answer:
P(40) = – 17 and P(80) = – 21

Exercise 3.
Estimate the area of the cross section.
Answer:

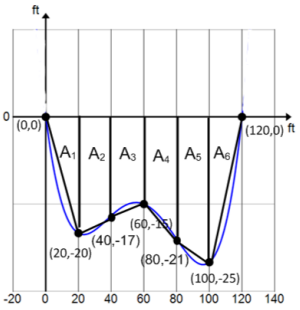
A = A₁ + A₂ + A₃ + A₄ + A₅ + A₆
= 200 ft² + 370 ft² + 320 ft² + 360 ft² + 460 ft² + 250 ft²
= 1,960 ft²

Suppose that the river flow speed was measured to be an average speed of 176\(\frac{\mathrm{ft}}{\min }\) at the cross section.

Exercise 4.
What is the volumetric flow of the water (the volume of water per minute)?
Answer:

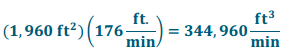
Exercise 5.
Convert the flow to gallons per minute. [Note: 1 cubic foot 7.48052 gallons.]
Answer:

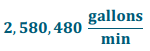
Eureka Math Algebra 2 Module 1 Lesson 21 Problem Set Answer Key

Question 1.
As the leader of the surveying team, write a short report to the EPA on your findings from the In-class exercises. Be sure to include data and calculations.
Answer:
After collecting data at the site, we decided that the cross-sectional area could be approximated using trapezoids. In order to Increase the accuracy of our area approximation, more data points were needed. We chose to use the data collected to model the riverbed using a degree 4 polynomial function. We used the computational knowledge engine Wolfram Alpha to find the polynomial that fit the data, which is P(x) = \(\frac{17}{3840000}\)x⁴ – \(\frac{33}{32000}\)x³ + \(\frac{751}{9600}\)x² – \(\frac{35}{16}\)x. Using the polynomial P, we were able to estimate enough data points to calculate the cross – sectional area and determined that it was 1,960 ft². Using this information and the average speed of the water at the cross-section, which was \(\frac{\text { ft}}{\min }\), we were able to compute the volumetric flow of the river at that cross-section. We determined that the volumetric flow is approximately 344,960 \(\frac{\mathrm{ft}^{3}}{\mathrm{min}}\) which is 2,580,480 \(\frac{\text { gallons }}{\text { min }}\).

Question 2.
Suppose that depths of the riverbed were measured for a different cross-section of the river.
a. Use Wolfram Alpha to find the interpolating polynomial Q with values:
Q(0) = 0,        Q(16.5) = – 27.4,       Q(44.4) = – 19.6,       Q(77.6) = -25.1,
Q(123. 3) = – 15.0,       Q(131. 1) = – 15. 1,       Q(150) = 0.
Answer:

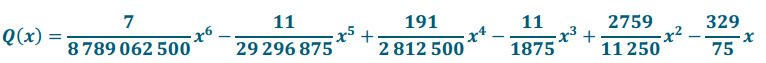
b. Sketch the cross-section of the river, and estimate its area.
Answer:

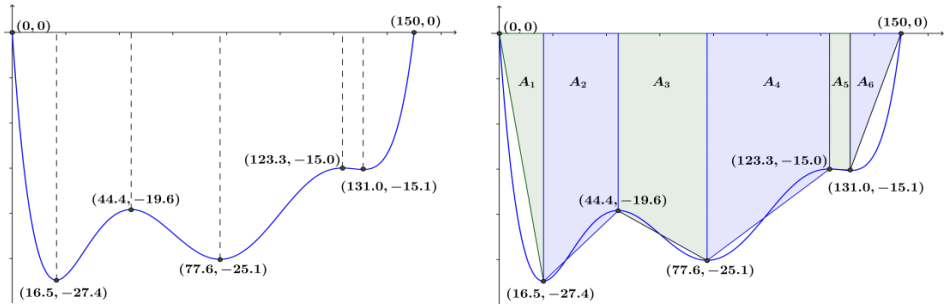
Area estimates:
A₁ = \(\frac{1}{2}\) (27.4)(16.5) = 226.05
A₂ = \(\frac{1}{2}\) (27.4 + 19.6) (44.4 – 16.5) = 655.65
A₃ = \(\frac{1}{2}\) (25.1 + 19.6) (77.6 – 44.4) = 742.02
A₄ = \(\frac{1}{2}\) (15. 0 + 25. 1) (123. 3 – 77.6) = 916.285
A₅ = \(\frac{1}{2}\) (15. 1 + 15.0) (131.0 – 123.3) = 115. 885
A₆ = \(\frac{1}{2}\)(15. 1) (150. 0 – 131.0) = 143.45
So, the total area can be estimated by
A = A₁ + A₂ + A₃ + A₄ + A₅ + A₆
= 2799.34.

c. Suppose that the speed of the water was measured at 124\(\frac{\text { ft}}{\text { min }}\) What is the approximate volumetric flow in this section of the river, measured in gallons per minute?
Answer:

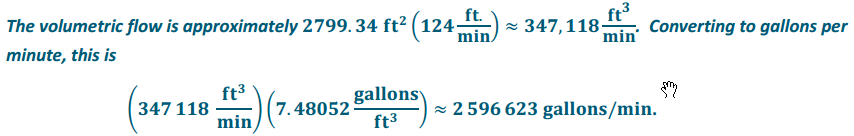
Eureka Math Algebra 2 Module 1 Lesson 21 Exit Ticket Answer Key

Explain the process you used to estimate the volumetric flow of the river, from accumulating the data to calculating the flow of water.
Answer:
We were given data points that represented the depth of the river at various points in the cross-section. We used Wolfram Alpha to find a polynomial P that passed through those given points. We used the polynomial P to find more data points. Then we approximated the area of the cross-section using triangles and trapezoids; figures whose area we know how to calculate. Once we had an approximate area of the cross-section, we multiplied that area by the speed of the water across the cross-section to find the amount of volumetric flow in units of cubic feet per minute. The last step was to convert cubic feet to gallons to get the amount of volumetric flow in units of gallons per minute.