Eureka Math Algebra 2 Module 1 Lesson 18 Answer Key

Engage NY Eureka Math Algebra 2 Module 1 Lesson 18 Answer Key

Eureka Math Algebra 2 Module 1 Lesson 18 Example Answer Key

Example 1.
a. Find the quotient by factoring the numerator.
$\frac{x^{2}+3 x+2}{x+2}$
Answer:
$\frac{x^{2}+3 x+2}{x+2}=\frac{(x+1)(x+2)}{x+2}$
= x + 1

→ We already know that $\frac{x^{2}+3 x+2}{x+2}$ = x + 1, as long as x ≠ – 2. How could we use this fact to find $\frac{x^{2}+3 x+5}{x+2}$?
Since 3 + 2 = 5, there must be 3 left over after performing division.

→ How could we rewrite the problem in a way that is more convenient?
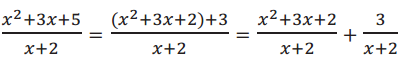
$Eureka Math Algebra 2 Module 1 Lesson 18 Example Answer Key 4$

→ So, what are the quotient and remainder?
The quotient is x + 1 with a remainder of 3.

Since the 3 is left over and has not been divided by the x + 2, it is still written as a quotient.
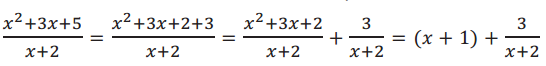
$Eureka Math Algebra 2 Module 1 Lesson 18 Example Answer Key 5$

b. Find the quotient.
$\frac{x^{2}+3 x+5}{x+2}$
Answer:
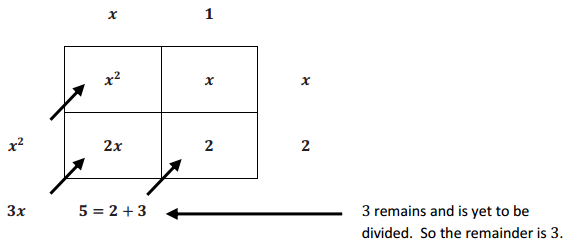
$Eureka Math Algebra 2 Module 1 Lesson 18 Example Answer Key 6$
$\frac{x^{2}+3 x+5}{x+2}$ = (x + 1) + $\frac{3}{x+2}$

Long Division Method:
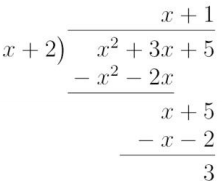
$Eureka Math Algebra 2 Module 1 Lesson 18 Example Answer Key 7$

Example 2.
a. Find the quotient by factoring the numerator.
$\frac{x^{3}-8}{x-2}$
Answer:
$\frac{(x-2)\left(x^{2}+2 x+4\right)}{x-2}$
= x² + 2x + 4

b. find the quotient.
$\frac{x^{3}-4}{x-2}$
Answer:
= $\frac{x^{3}-8+4}{x-2}=\frac{x^{3}-8}{x-2}+\frac{4}{x-2}$
= x² + 2x + 4 + $\frac{4}{x-2}$

→ In pairs, see if you can determine how to use the quotient from (a) to find the quotient of $\frac{x^{3}-4}{x-2}$
Give students a couple of minutes to discuss, and then elicit responses.

→ How did you rewrite the numerator?
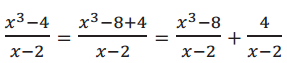
$Eureka Math Algebra 2 Module 1 Lesson 18 Example Answer Key 8$

→ Why is this a useful way to rewrite the problem?
We know that $\frac{x^{3}-8}{x-2}$ = x² + 2x + 4.

→ So what are the quotient and remainder of $\frac{x^{3}-4}{x-2}$ ?
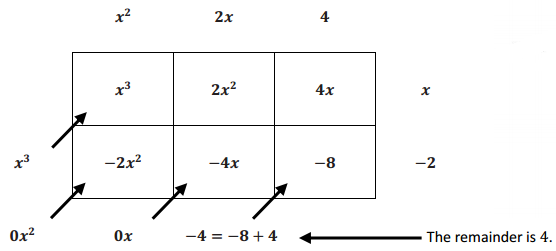
The quotient is x² + 2x + 4 with a remainder of 4.

Therefore, $\frac{x^{3}-4}{x-2}$ = (x² + 2x + 4) + $\frac{4}{x-2}$

Give students a couple of minutes to rework the problem using either the reverse tabular method or long division and then share student work.
$Eureka Math Algebra 2 Module 1 Lesson 18 Example Answer Key 9$
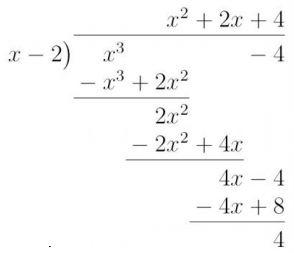
$Eureka Math Algebra 2 Module 1 Lesson 18 Example Answer Key 10$

Eureka Math Algebra 2 Module 1 Lesson 18 Opening Exercise Answer Key

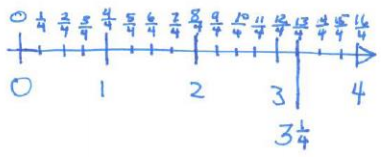
Write the rational number $\frac{13}{4}$ as aa mixed number.
Answer:
Method 1:
$Eureka Math Algebra 2 Module 1 Lesson 18 Opening Exercise Answer Key 1$

Method 2:
$Eureka Math Algebra 2 Module 1 Lesson 18 Opening Exercise Answer Key 2$

Method 3:
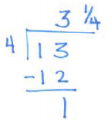
$Eureka Math Algebra 2 Module 1 Lesson 18 Opening Exercise Answer Key 3$

Eureka Math Algebra 2 Module 1 Lesson 18 Exercise Answer Key

Find each quotient by inspection.

Exercise 1.
$\frac{x+4}{x+1}$
Answer:
1 + $\frac{3}{x+1}$

Exercise 2.
$\frac{2 x-7}{x-3}$
Answer:
2 – $\frac{1}{x-3}$

Exercise 3.
$\frac{x^{2}-21}{x+4}$
Answer:
(x – 4) – $\frac{5}{x+4}$

Find each quotient by using the reverse tabular method.

Exercise 4.
$\frac{x^{2}+4 x+10}{x-8}$
Answer:
(x + 12) + $\frac{106}{x-8}$

Exercise 5.
$\frac{x^{3}-x^{2}+3 x-1}{x+3}$
Answer:
x² – 4x + 12 – $\frac{46}{x+3}$

Exercise 6.
$\frac{x^{2}-2 x-19}{x-1}$
Answer:
(x – 1) – $\frac{20}{x-1}$

Find each quotient by using long division.

Exercise 7.
$\frac{x^{2}-x-25}{x+6}$
Answer:
(x – 7) + $\frac{17}{x+6}$

Exercise 8.
$\frac{x^{4}-8 x^{2}+12}{x+2}$
Answer:
(x³ – 2x² – 4x + 8) – $\frac{4}{x+2}$

Exercise 9.
$\frac{4 x^{3}+5 x-8}{2 x-5}$
Answer:
(2x² + 5x + 15) + $\frac{67}{2 x-5}$

Rewrite the numerator in the form (x – h)² + k by completing the square. Then find the quotient.

Exercise 10.
$\frac{x^{2}+4 x-9}{x+2}$
Answer:
(x + 2) – $\frac{13}{x+2}$

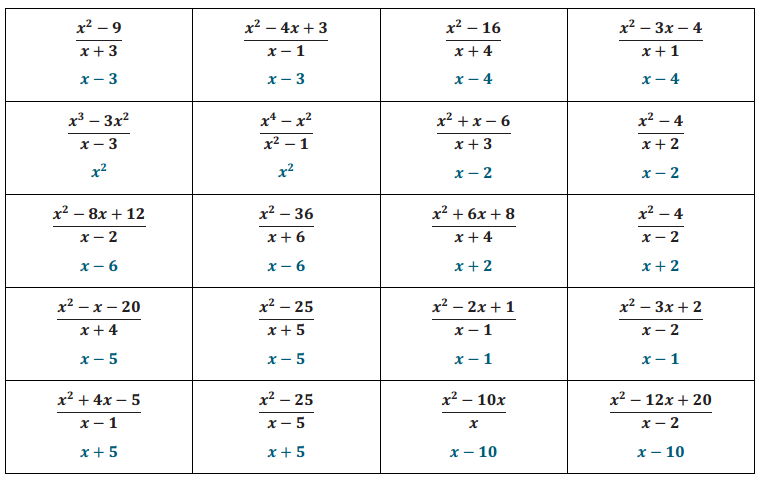
Eureka Math Algebra 2 Module 1 Lesson 18 Mental Math Exercise Answer Key

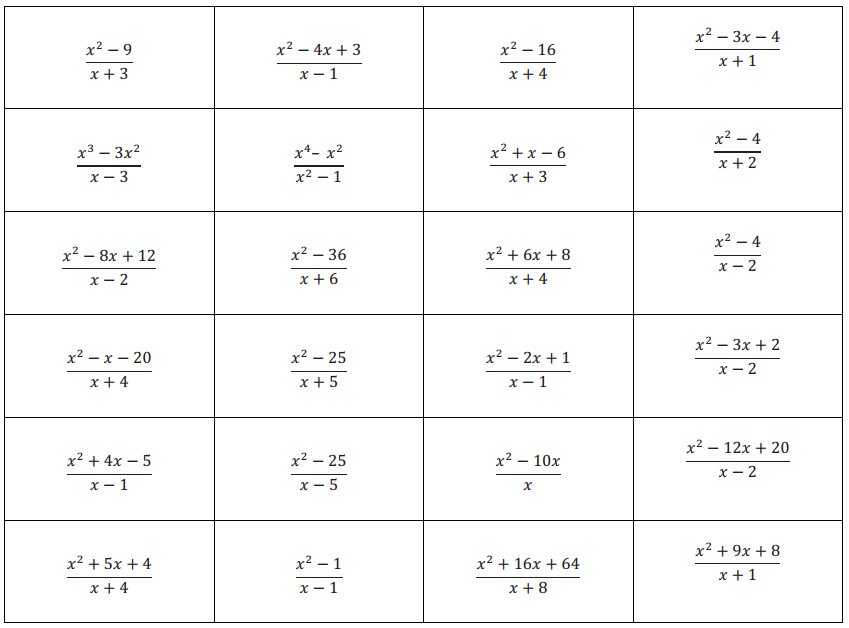
$Eureka Math Algebra 2 Module 1 Lesson 18 Mental Math Exercise Answer Key 11$
Answer:
$Eureka Math Algebra 2 Module 1 Lesson 18 Mental Math Exercise Answer Key 12$
$Eureka Math Algebra 2 Module 1 Lesson 18 Mental Math Exercise Answer Key 13$

Eureka Math Algebra 2 Module 1 Lesson 18 Problem Set Answer Key

Question 1.
For each pair of problems, find the first quotient by factoring the numerator. Then, find the second quotient by using the first quotient.
a. $\frac{3 x-6}{x-2}$ $\frac{3 x-9}{x-2}$
Answer:
3 3 – $\frac{3}{x-2}$

b. $\frac{x^{2}-5 x-14}{x-7}$ $\frac{x^{2}-5 x+2}{x-7}$
Answer:
x + 2 (x + 2) + $\frac{16}{x-7}$

c. $\frac{x^{3}+1}{x+1}$ $\frac{x^{3}}{x+1}$
Answer:
x² – x + 1 (x² – x + 1) – $\frac{1}{x+1}$

d. $\frac{x^{2}-13 x+36}{x-4}$ $\frac{x^{2}-13 x+30}{x-4}$
Answer:
x – 9 (x – 9) – $\frac{6}{x-4}$

Find each quotient by using reverse tabular method.

Question 2.
$\frac{x^{3}-9 x^{2}+5 x+2}{x-1}$
Answer:
(x² – 8x – 3) – $\frac{1}{x-1}$

Question 3.
$\frac{x^{2}+x+10}{x+12}$
Answer:
(x – 11) + $\frac{142}{x+12}$

Question 4.
$\frac{2 x+6}{x-8}$
Answer:
2 + $\frac{22}{x-8}$

Question 5.
$\frac{x^{2}+8}{x+3}$
Answer:
(x – 3) + $\frac{17}{x+3}$

Find each quotient by using long division.

Question 6.
$\frac{x^{4}-9 x^{2}+10 x}{x+2}$
Answer:
(x³ – 2x² – 5x + 20) – $\frac{40}{x+2}$

Question 7.
$\frac{x^{5}-35}{x-2}$
Answer:
(x^>4 + 2x³ + 4x² + 8x + 16) – $\frac{3}{x-2}$

Question 8.
$\frac{x^{2}}{x-6}$
Answer:
(x + 6) + $\frac{36}{x-6}$

Question 9.
$\frac{x^{3}+2 x^{2}+8 x+1}{x+5}$
Answer:
(x² – 3x + 23) – $\frac{114}{x+5}$

Question 10.
$\frac{x^{3}+2 x+11}{x-1}$
Answer:
(x² + x + 3) + $\frac{14}{x-1}$

Question 11.
$\frac{x^{4}+3 x^{3}-2 x^{2}+6 x-15}{x}$
Answer:
(x³ + 3x² – 2x + 6) – $\frac{15}{x}$

Question 12.
Rewrite the numerator in the form (x – h)² + k by completing the square. Then, find the quotient.
$\frac{x^{2}-6 x-10}{x-3}$
Answer:
x – 3 – $\frac{19}{x-3}$

Eureka Math Algebra 2 Module 1 Lesson 18 Exit Ticket Answer Key

Question 1.
Find the quotient of $\frac{x-6}{x-8}$ by inspection.
Answer:
1 + $\frac{2}{x-8}$

Question 2.
Find the quotient of $\frac{9 x^{3}-12 x^{2}+4}{x-2}$ by using either long division or the reverse tabular method.
Answer:
(9x² + 6x + 12) + $\frac{28}{x-2}$