Engage NY Eureka Math Algebra 1 Module 4 Lesson 19 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 19 Example Answer Key
Example
For each graph, answer the following:
- What is the parent function?
- How does the translated graph relate to the graph of the parent function?
- Write the formula for the function depicted by the translated graph.
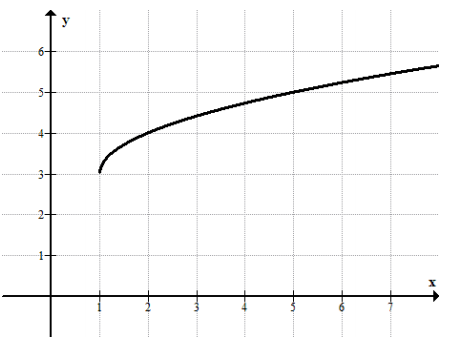
a.
Answer:
y = f(x)
y = g(x)
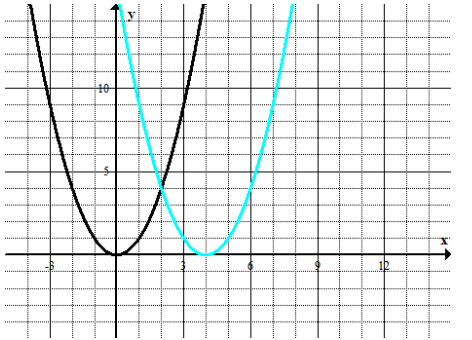
The parent function is f(x) = x2. The graph is shifted 4 units to the right. The function defined by the translated graph is g(x) = (x – 4)2.
b.
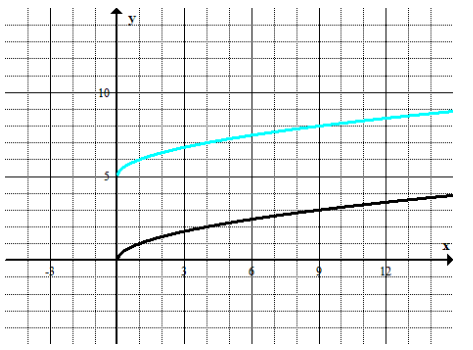
Answer:
y = f(x)
y = g(x)
The parent function is f(x) = \(\sqrt{x}\). The constant value added to f(x) is 5 because the graph is shifted 5 units up. The function defined by the translated graph is g(x) = \(\sqrt{x}\) + 5.
c.
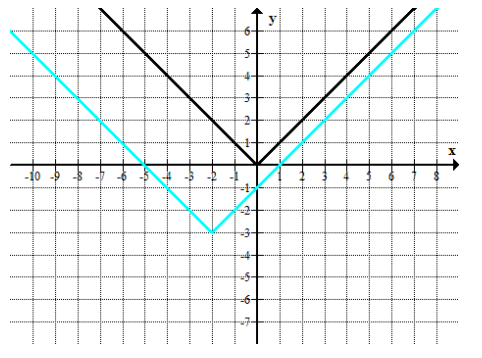
Answer:
y = f(x)
y = g(x)
The parent function is f(x) = |x|. The constant values added to f(x) are – 3 and + 2 because the graph is shifted 3 units down and 2 units to the left. The function defined by the translated graph is g(x) = |x + 2| – 3.
Eureka Math Algebra 1 Module 4 Lesson 19 Exercise Answer Key
Opening Exercise
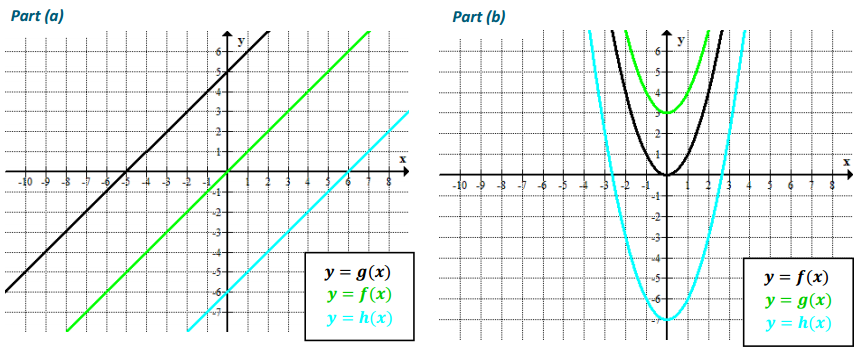
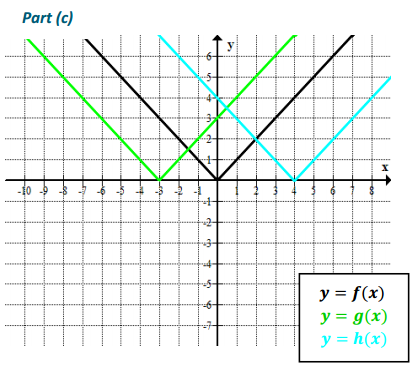
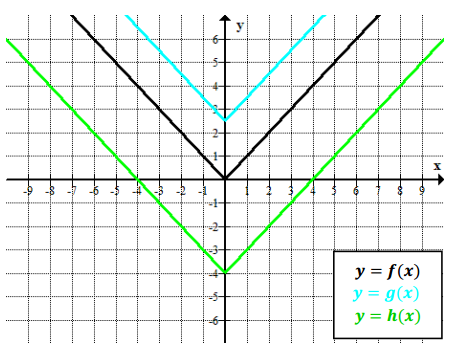
Graph each set of three functions in the same coordinate plane (on your graphing calculator or a piece of graph paper). Then, explain what similarities and differences you see among the graphs.
a. f(x) = x
g(x) = x + 5
h(x) = x – 6
b. f(x) = x2
g(x) = x2 + 3
h(x) = x2 – 7
c. f(x) = |x|
g(x) = |x + 3|
h(x) = |x – 4|
Answer:
Part (a)—The graphs are parallel lines, but they have different x – and y – intercepts.
Part (b)—The graphs look the same (because they are congruent), but they have different vertices, which in this case means different minimum values. They are related by vertical translations.
Part (c)—The overall shapes of the graphs look the same (because they are congruent), but they have different vertices. They are related by horizontal translations.
Exercises
Exercise 1.
For each of the following graphs, use the formula for the parent function f to write the formula of the translated function.
a.
Answer:
Parent Function: f(x) = |x|
Translated Functions: g(x) = |x| + 2.5,
h(x) = |x| – 4
b.
Answer:
Parent Function: f(x) = \(\sqrt [ 3 ]{ x }\)
Translated Functions: g(x) = \(\sqrt [ 3 ]{ x }\) + 1,
h(x) = \(\sqrt [ 3 ]{ x + 5 }\)
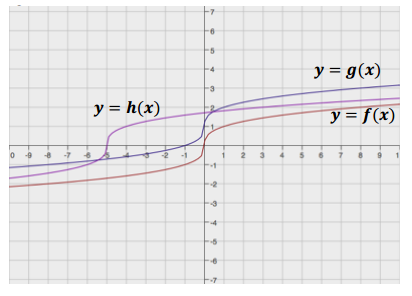
Exercise 2.
Below is a graph of a piecewise function f whose domain is – 5 ≤ x ≤ 3. Sketch the graphs of the given functions on the same coordinate plane. Label your graphs correctly.
g(x) = f(x) + 3 h(x) = f(x – 4)
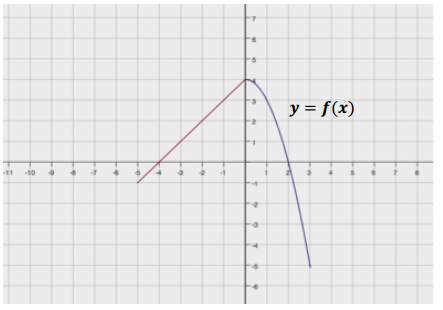
Answer:
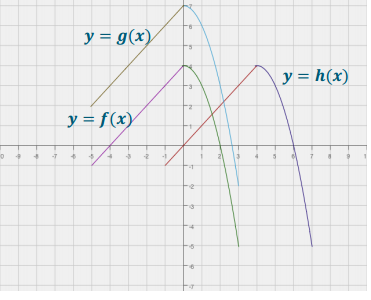
Exercise 3.
Match the correct equation and description of the function with the given graphs.
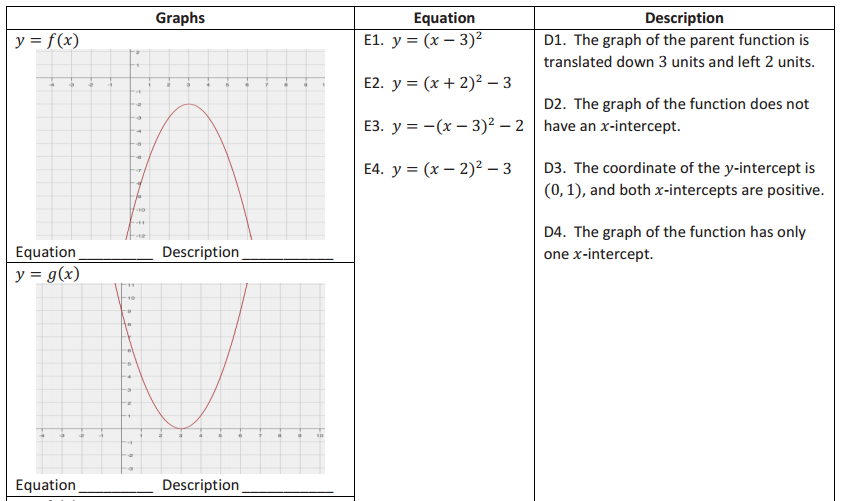
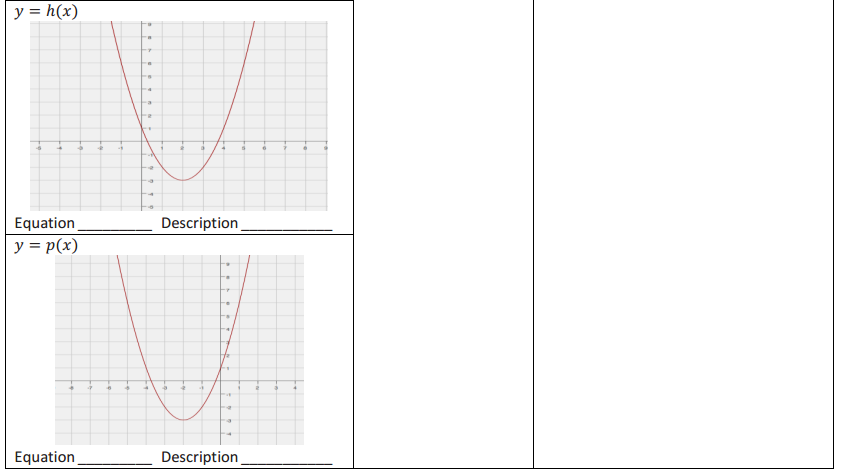
Answer:
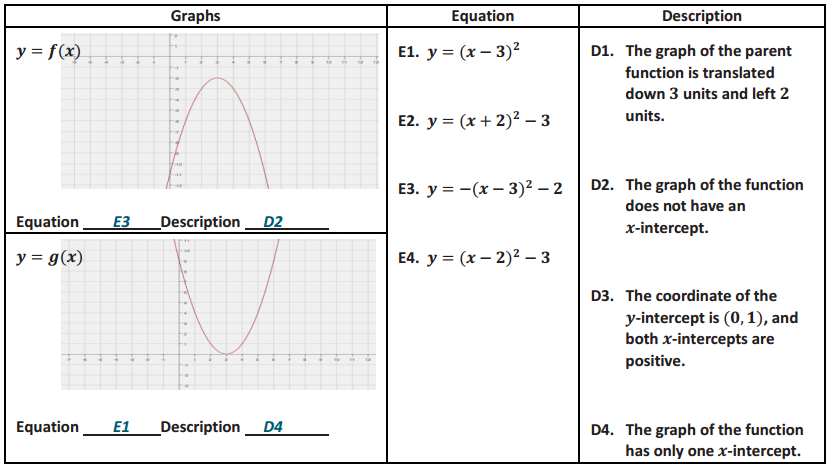
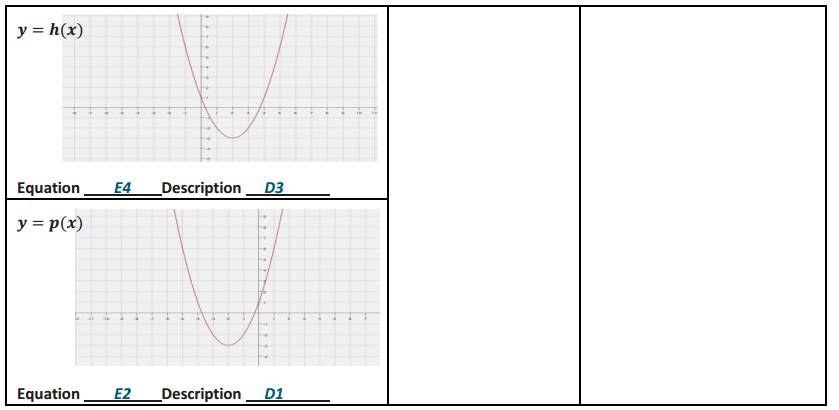
Eureka Math Algebra 1 Module 4 Lesson 19 Problem Set Answer Key
Question 1.
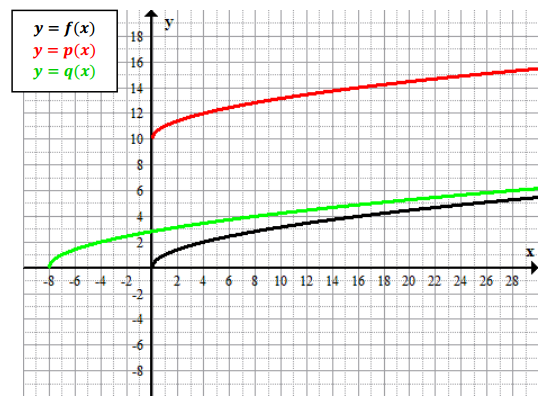
Graph the functions in the same coordinate plane. Do not use a graphing calculator.
f(x) = \(\sqrt{x}\)
p(x) = 10 + \(\sqrt{x}\)
q(x) = \(\sqrt{x + 8}\)

Answer:
Question 2.
Write a function that translates the graph of the parent function f(x) = x2 down 7.5 units and right 2.5 units.
Answer:
f(x) = (x – 2.5)2 – 7.5
Question 3.
How would the graph of f(x) = |x| be affected if the function were transformed to f(x) = |x + 6| + 10?
Answer:
The graph would be shifted 10 units up and 6 units to the left.
Question 4.
Below is a graph of a piecewise function f whose domain is the interval – 4≤x≤2. Sketch the graph of the given functions below. Label your graphs correctly.
g(x) = f(x) – 1 h(x) = g(x – 2) [Be careful; this one might be a challenge.]
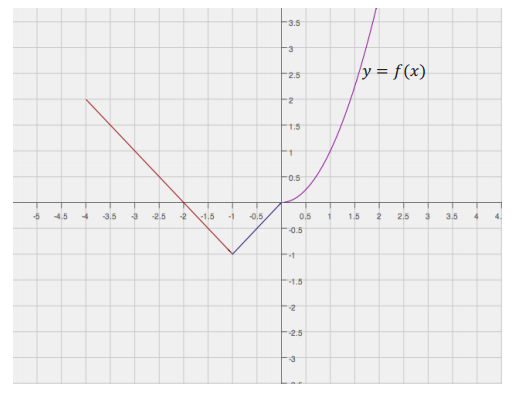
Answer:
Point out that the graph of h is related to g rather than f. Make sure students recognize that they must find the graph of g first, and then translate it to find h.
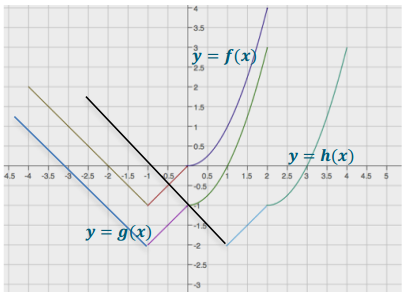
Question 5.
Study the graphs below. Identify the parent function and the transformations of that function depicted by the second graph. Then, write the formula for the transformed function.
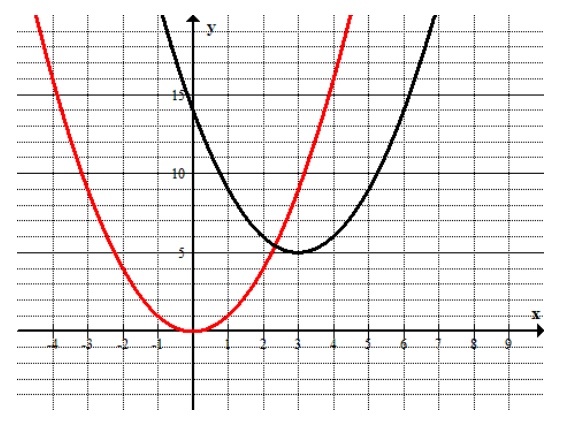
Answer:
y = g(x)
y = f(x)
The parent function is f(x) = x2, in red. The graph of the transformed function, in black, is the graph of y = f(x) shifted 3 units to the right and 5 units up. The function defined by the translated graph is g(x) = (x – 3)2 + 5.
Eureka Math Algebra 1 Module 4 Lesson 19 Exit Ticket Answer Key
Question 1.
Ana sketched the graphs of f(x) = x2 and g(x) = x2 – 6 as shown below. Did she graph both of the functions correctly? Explain how you know.
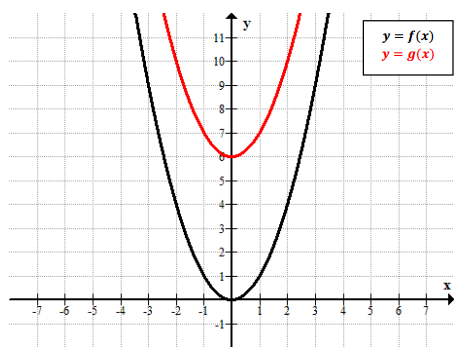
Answer:
The function f was graphed correctly, but not g. The graph of g should have been translated 6 units below the graph of f.
Question 2.
Use transformations of the graph of f(x) = \(\sqrt{x}\) to sketch the graph of f(x) = \(\sqrt{x – 1}\) + 3.

Answer:
The graph should depict the graph of the square root function translated 1 unit right and 3 units up.