Engage NY Eureka Math Algebra 1 Module 4 Lesson 15 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 15 Exercise Answer Key
Opening Exercise
Solve the following:
a. 4x2 + 5x + 3 = 2x2 – 3x
Answer:
Students should recognize that this is a difficult quadratic equation to solve. Accordingly, they should set it equal to zero and solve it using the quadratic formula:
2x2 + 8x + 3 = 0
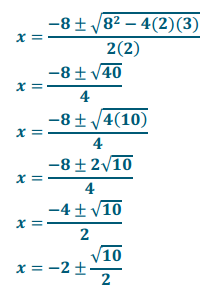
Check by substituting the approximated decimal value(s) into the original equation or by completing the square:
2(x2 + 4x) = – 3 → 2(x2 + 4x + 4) = – 3 + 8 → 2(x + 2)2 = 5
(x + 2)2 = \(\frac{5}{2}\) → x + 2 = ±\(\sqrt{\frac{5}{2}}\) → x = – 2 ± \(\sqrt{\frac{5}{9}}\)
(Have students use their calculators to check that these are the same decimal values as the previous solutions.)
b. c2 – 14 = 5c
Answer:
Initially, students may approach this problem by using the quadratic formula. While this approach works, encourage students to look for a more efficient pathway to the solution (in this case, to solve by factoring):
c2 – 5c – 14 = 0 → (c – 7)(c + 2) = 0 → c = 7 or – 2
Checks:
72 – 14 = 5(7) → 49 – 14 = 35 → 35 = 35
( – 2)2 – 14 = 5( – 2) → 4 – 14 = – 10 → – 10 = – 10
Exercises
Solve Exercises 1–5 using the quadratic formula.
Exercise 1.
x2 – 2x + 1 = 0
Answer:
a = 1, b = – 2, c = 1
x = \(\frac{ – ( – 2) \pm \sqrt{( – 2)^{2} – 4(1)(1)}}{2(1)}\) = \(\frac{2 \pm \sqrt{0}}{2}\) = 1
Exercise 2.
3b2 + 4b + 8 = 0
Answer:
a = 3, b = 4, c = 8
b = \(\frac{ – 4 \pm \sqrt{4^{2} – 4(3)(8)}}{2(3)}\) = \(\frac{ – 4 \pm \sqrt{ – 80}}{6}\) = ???
Exercise 3.
2t2 + 7t – 4 = 0
Answer:
a = 2, b = 7, c = – 4
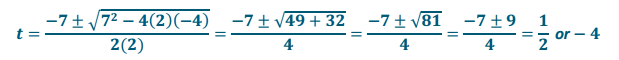
Exercise 4.
q2 – 2q – 1 = 0
Answer:
a = 1, b = – 2, c = – 1
q = \(\frac{ – ( – 2) \pm \sqrt{( – 2)^{2} – 4(1)( – 1)}}{2(1)}\) = \(\frac{2 \pm \sqrt{8}}{2}\) = \(\frac{2 \pm 2 \sqrt{2}}{2}\) = 1 ± \(\sqrt{2}\)
Exercise 5.
m2 – 4 = 3
Answer:
a = 1, b = 0, c = – 7
m = \(\frac{0 \pm \sqrt{0^{2} – 4( – 7)}}{2(1)}\) = \(\frac{0 \pm \sqrt{28}}{2}\) = \(\frac{0 \pm 2 \sqrt{7}}{2}\) = 0 ± \(\sqrt{7}\) = ±\(\sqrt{7}\)
For Exercises 6–9, determine the number of real solutions for each quadratic equation without solving.
Exercise 6.
p2 + 7p + 33 = 8 – 3p
Answer:
a = 1, b = 10, c = 25 → 102 – 4(1)(25) = 0 → one real solution
Exercise 7.
7x2 + 2x + 5 = 0
Answer:
a = 7, b = 2, c = 5 → 22 – 4(7)(5) = – 136 → no real solutions
Exercise 8.
2y2 + 10y = y2 + 4y – 3
Answer:
a = 1, b = 6, c = 3 → 62 – 4(1)(3) = 24 → two real solutions
Exercise 9.
4z2 + 9 = – 4z
Answer:
a = 4, b = 4, c = 9 → 42 – 4(4)(9) = – 128 → no real solutions
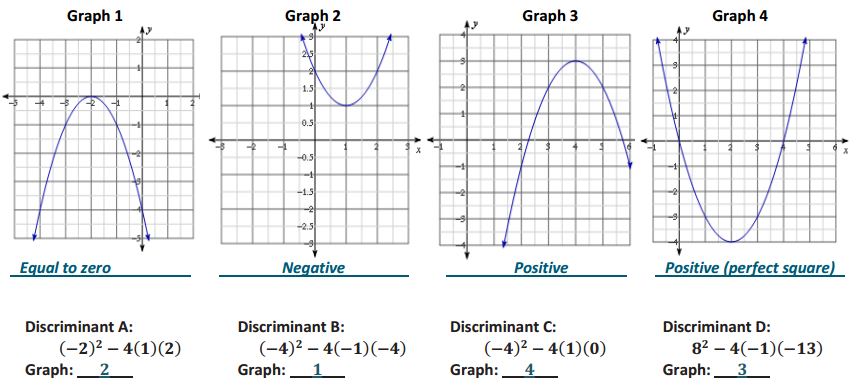
Exercise 10.
On the line below each graph, state whether the discriminant of each quadratic equation is positive, negative, or equal to zero. Then, identify which graph matches the discriminants below.
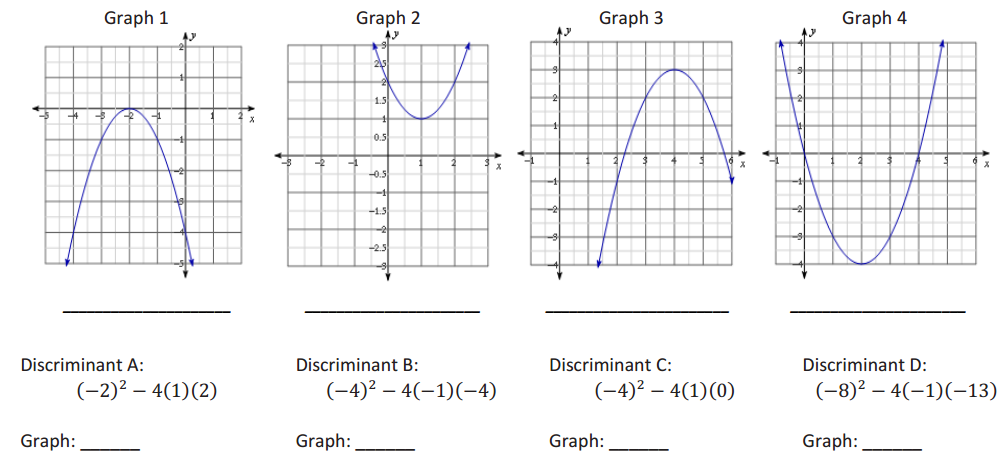
Answer:
Exercise 11.
Consider the quadratic function f(x) = x2 – 2x – 4.
a. Use the quadratic formula to find the x – intercepts of the graph of the function.
Answer:
x = 1 + \(\sqrt{5}\) and x = 1 – \(\sqrt{5}\)
b. Use the x – intercepts to write the quadratic function in factored form.
Answer:
f(x) = (x – (1 + \(\sqrt{5}\)))(x – (1 – \(\sqrt{5}\)))
c. Show that the function from part (b) written in factored form is equivalent to the original function.
Answer:
f(x) = x2 – (1 + \(\sqrt{5}\))x – (1 – \(\sqrt{5}\))x + (1 + \(\sqrt{5}\))(1 – \(\sqrt{5}\))
f(x) = x2 – x – \(\sqrt{5}\) x – x + \(\sqrt{5}\) x + 1 – 5
f(x) = x2 – 2x – 4
Extension: Consider the quadratic equation ax2 + bx + c = 0.
a. Write the equation in factored form, a(x – m)(x – n) = 0, where m and n are the solutions to the equation.
Answer:

Eureka Math Algebra 1 Module 4 Lesson 15 Problem Set Answer Key
Without solving, determine the number of real solutions for each quadratic equation.
Question 1.
b2 – 4b + 3 = 0
Answer:
a = 1, b = – 4, c = 3 → ( – 4)2 – 4(1)(3) = 4 → two real solutions
Question 2.
2n2 + 7 = – 4n + 5
Answer:
a = 2, b = 4, c = 2 → (4)2 – 4(2)(2) = 0 → one real solution
Question 3.
x – 3x2 = 5 + 2x – x2
Answer:
a = – 2, b = – 1, c = – 5 → ( – 1)2 – 4( – 2)( – 5) = – 39 → no real solutions
Question 4.
4q + 7 = q2 – 5q + 1
Answer:
a = – 1, b = 9, c = 6 → (9)2 – 4( – 1)(6) = 105 → two real solutions
Based on the graph of each quadratic function, y = f(x), determine the number of real solutions for each corresponding quadratic equation, f(x) = 0.
Question 5.
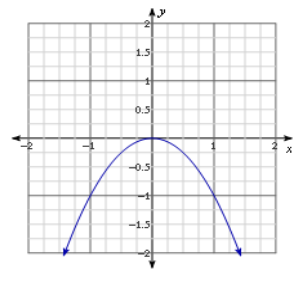
Answer:
One real solution
Question 6.
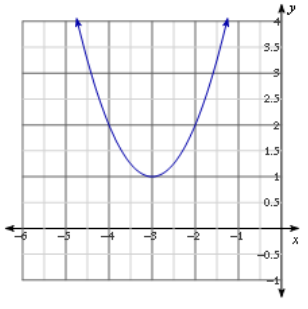
Answer:
No real solutions
Question 7.
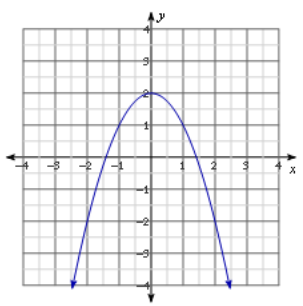
Answer:
Two real solutions
Question 8.
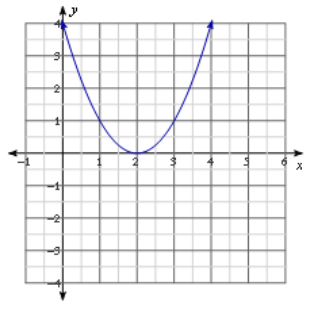
Answer:
One real solution
Question 9.
Consider the quadratic function f(x) = x2 – 7.
a. Find the x – intercepts of the graph of the function.
Answer:
x = ±\(\sqrt{7}\)
b. Use the x – intercepts to write the quadratic function in factored form.
Answer:
f(x) = (x – \(\sqrt{7}\))(x + \(\sqrt{7}\))
c. Show that the function from part (b) written in factored form is equivalent to the original function.
Answer:
f(x) = (x – \(\sqrt{7}\))(x + \(\sqrt{7}\)) = x2 + \(\sqrt{7}\) x – \(\sqrt{7}\) x – 7 = x2 – 7
Question 10.
Consider the quadratic function f(x) = – 2x2 + x + 5.
a. Find the x – intercepts of the graph of the function.
Answer:
x = \(\frac{1 \pm \sqrt{41}}{4}\)
b. Use the x – intercepts to write the quadratic function in factored form.
Answer:
f(x) = – 2(x – \(\frac{1 + \sqrt{41}}{4}\)) (x – \(\frac{1 – \sqrt{41}}{4}\))
c. Show that the function from part (b) written in factored form is equivalent to the original function.
Answer:
f(x) = – 2(x – \(\frac{1 + \sqrt{41}}{4}\))(x – \(\frac{1 – \sqrt{41}}{4}\)) = – 2(x2 – \(\frac{1 + \sqrt{41}}{4}\) x – \(\frac{1 – \sqrt{41}}{4}\)x – \(\frac{5}{2}\)) = – 2(x2 – \(\frac{1}{2}\) x – \(\frac{5}{2}\))
= – 2x2 + x + 5
Eureka Math Algebra 1 Module 4 Lesson 15 Exit Ticket Answer Key
Question 1.
Solve the following equation using the quadratic formula: 3x2 + 6x + 8 = 6.
Answer:
3x2 + 6x + 2 = 0 →
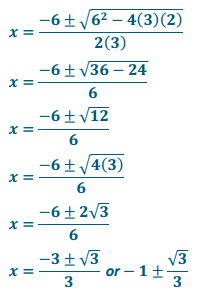
Question 2.
Is the quadratic formula the most efficient way to solve this equation? Why or why not?
Answer:
This is a personal preference. Some may consider the quadratic formula to be more efficient, while others may prefer completing the square. After the leading coefficient is factored out, the linear term coefficient is still even, making this a good candidate for completing the square.
Question 3.
How many zeros does the function f(x) = 3x2 + 6x + 2 have? Explain how you know.
Answer:
Since the discriminant of the original equation is positive, 12, and yields two real solutions, the function must have two zeros. OR After solving the equation 3x2 + 6x + 2 = 0, I found that there were two irrational solutions. This means that the corresponding function has two zeros.