Engage NY Eureka Math Algebra 1 Module 4 Lesson 1 Answer Key
Eureka Math Algebra 1 Module 4 Lesson 1 Example Answer Key
Example 1.
Jackson has given his friend a challenge:
The area of a rectangle, in square units, is represented by 3a2 + 3a for some real number a. Find the length and width of the rectangle.
How many possible answers are there for Jackson’s challenge to his friend? List the answer(s) you find.

Answer:
3a2 + 3a = 3a(a + 1) so the width of the rectangle could be 3a units and the length could be (a + 1) units.
(Students may opt to factor only a or 3 or even \(\frac{1}{2}\) a: a(3a + 3) or 3(a2 + a) or \(\frac{1}{2}\) a(6a + 6).)
There are infinite representations for the dimensions of the rectangle.
Example 2: Multiply Two Binomials
Using a Table as an Aid
You have seen the geometric area model used in previous examples to demonstrate the multiplication of polynomial expressions for which each expression was known to represent a measurement of length.
Without a context such as length, we cannot be certain that a polynomial expression represents a positive quantity.
Therefore, an area model is not directly applicable to all polynomial multiplication problems. However, a table can be used in a similar fashion to identify each partial product as we multiply polynomial expressions. The table serves to remind us of the area model even though it does not represent area.
For example, fill in the table to identify the partial products of (x + 2)(x + 5). Then, write the product of (x + 2)(x + 5) in standard form.
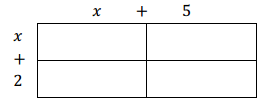
Answer:
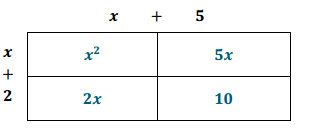
x2 + 7x + 10
Without the Aid of a Table
Regardless of whether or not we make use of a table as an aid, the multiplying of two binomials is an application of the distributive property. Both terms of the first binomial distribute over the second binomial. Try it with (x + y)(x – 5). In the example below, the colored arrows match each step of the distribution with the resulting partial product.
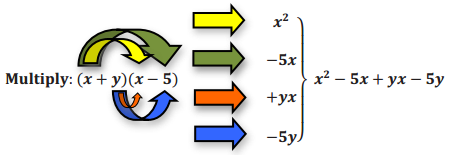
Example 3: The Difference of Squares
Find the product of (x + 2)(x – 2). Use the distributive property to distribute the first binomial over the second.
With the Use of a Table:
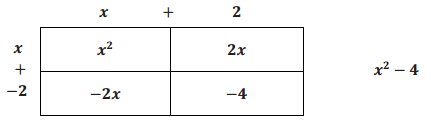
Without the Use of a Table:
(x)(x) + (x)( – 2) + (2)(x) + (2)( – 2) = x2 – 2x + 2x – 4 = x2 – 4
Answer:
→ Do you think the linear terms are always opposites when we multiply the sum and difference of the same two terms? Why?
Yes. When we multiply the first term of the first binomial by the last term of the second, we get the opposite of what we get when we multiply the second term of the first binomial by the first term of the second.
→ So, x2 – 4 is the difference of two perfect squares. Factoring the difference of two perfect squares reverses the process of finding the product of the sum and difference of two terms.
Example 4: The Square of a Binomial
To square a binomial, such as (x + 3)2, multiply the binomial by itself.
(x + 3)(x + 3) = (x)(x) + (x)(3) + (3)(x) + (3)(3)
= x2 + 3x + 3x + 9
= x2 + 6x + 9
Square the following general examples to determine the general rule for squaring a binomial:
a.(a + b)2
Answer:
(a + b)(a + b) = a2 + ab + ba + b2 = a2 + 2ab + b2
b.(a – b)2
Answer:
(a – b)(a – b) = a2 – ab – ba + b2 = a2 – 2ab + b2
Eureka Math Algebra 1 Module 4 Lesson 1 Exercise Answer Key
Opening Exercise
Write expressions for the areas of the two rectangles in the figures given below.
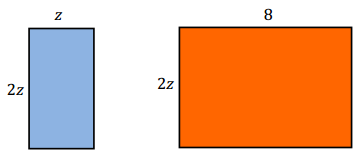
Answer:
Blue: 2z(z) = 2z2; Orange: 2z(8) = 16z
Now write an expression for the area of this rectangle:
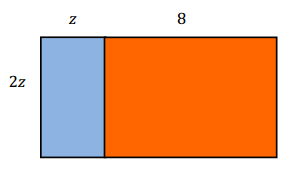
Answer:
2z2 + 16z
Exercises 1–3
Factor each by factoring out the greatest common factor:
Exercise 1.
10ab + 5a
Answer:
5a(2b + 1)
Exercise 2.
3g3 h – 9g2 h + 12h
Answer:
3h(g3 – 3g2 + 4)
Exercise 3.
6x2 y3 + 9xy4 + 18y5
Answer:
3y3 (2x2 + 3xy + 6y2) (Students may find this one to be more difficult. It is used as an example in a scaffolding suggestion below.)
Discussion: The Language of Polynomials
PRIME NUMBER: A prime number is a positive integer greater than 1 whose only positive integer factors are 1 and itself.
COMPOSITE NUMBER: A composite number is a positive integer greater than 1 that is not a prime number.
A composite number can be written as the product of positive integers with at least one factor that is not 1 or itself.
For example, the prime number 7 has only 1 and 7 as its factors. The composite number 6 has factors of 1, 2, 3, and 6; it could be written as the product 2⋅3.
Answer:
Factoring is the reverse process of multiplication (through multiple use of the distributive property). We factor a polynomial by reversing the distribution process—factoring the GCF out of each term and writing it on the outside of the parentheses. To check whether the polynomial’s factored form is equivalent to its expanded form, you can multiply the factors to see if the product yields the original polynomial.
4(x + 3) is called a factored form of 4x + 12.
A nonzero polynomial expression with integer coefficients is said to be prime or irreducible over the integers if it satisfies two conditions:
(1) It is not equivalent to 1 or – 1, and
(2) If the polynomial is written as a product of two polynomial factors, each with integer coefficients, then one of the two factors must be 1 or – 1.
Answer:
→ Note that this definition actually specifies prime numbers and their negatives as well (the case when the polynomial has degree 0).
→ For example: 4x + 9 is irreducible over the integers.
Given a polynomial in standard form with integer coefficients, let c be the greatest common factor of all of the coefficients. The polynomial is factored completely over the integers when it is written as a product of c and one or more prime polynomial factors, each with integer coefficients.
Answer:
→ In the future, we learn to factor over the rationals and reals.
Exercise 4.
Factor the following examples of the difference of perfect squares.
a. t2 – 25
Answer:
(t – 5)(t + 5)
b. 4x2 – 9
Answer:
(2x – 3)(2x + 3)
c. 16h2 – 36k2
Answer:
(4h – 6k)(4h + 6k)
d. 4 – b2
Answer:
(2 – b)(2 + b)
e. x4 – 4
Answer:
(x2 – 2)(x2 + 2)
f. x6 – 25
Answer:
(x3 – 5)(x3 + 5)
Write a General Rule for Finding the Difference of Squares
Write a2 – b2 in factored form.
Answer:
(a + b)(a – b)
Exercises 5–7
Factor each of the following differences of squares completely:
Exercise 5.
9y2 – 100z2
Answer:
(3y + 10z)(3y – 10z)
Exercise 6.
a4 – b6
(a2 + b3)(a2 – b3)
Exercise 7.
r4 – 16s4 (Hint: This one factors twice.)
Answer:
(r2 + 4s2)(r2 – 4s2) = (r2 + 4s2)(r – 2s)(r + 2s)
Exercises 8–9
Square the binomial.
Exercise 8.
(a + 6)2
Answer:
a2 + 12a + 36
Exercise 9.
(5 – w)2
Answer:
25 – 10w + w2
Eureka Math Algebra 1 Module 4 Lesson 1 Problem Set Answer Key
Question 1.
For each of the following, factor out the greatest common factor:
a. 6y2 + 18
Answer:
6(y2 + 3)
b. 27y2 + 18y
Answer:
9y(3y + 2)
c. 21b – 15a
Answer:
3(7b – 5a)
d. 14c2 + 2c
Answer:
2c(7c + 1)
e. 3x2 – 27
Answer:
3(x2 – 9)
Question 2.
Multiply.
a. (n – 5)(n + 5)
Answer:
n2 – 25
b. (4 – y)(4 + y)
Answer:
16 – y2
c. (k + 10)2
Answer:
k2 + 20k + 100
d. (4 + b)2
Answer:
16 + 8b + b2
Question 3.
The measure of a side of a square is x units. A new square is formed with each side 6 units longer than the original square’s side. Write an expression to represent the area of the new square. (Hint: Draw the new square and count the squares and rectangles.)
Original square x
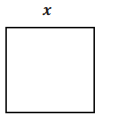
Answer:
New square:
(x + 6)2 or x2 + 12x + 36
Question 4.
In the accompanying diagram, the width of the inner rectangle is represented by x – 3 and the length by x + 3. The width of the outer rectangle is represented by 3x – 4 and the length by 3x + 4.

a. Write an expression to represent the area of the larger rectangle.
Answer:
Find the area of the larger (outer) rectangle by multiplying the binomials:
(3x – 4)(3x + 4) = 9x2 – 16.
b. Write an expression to represent the area of the smaller rectangle.
Answer:
Find the area of the smaller (inner) rectangle by multiplying the binomials:
(x – 3)(x + 3) = x2 – 9.
c. Express the area of the region inside the larger rectangle but outside the smaller rectangle as a polynomial in terms of x. (Hint: You will have to add or subtract polynomials to get your final answer.)
Answer:
Subtract the area of the smaller rectangle from the area of the larger rectangle:
(9x2 – 16) – (x2 – 9) = 9x2 – 16 – x2 + 9 = 8x2 – 7.
Eureka Math Algebra 1 Module 4 Lesson 1 Exit Ticket Answer Key
Question 1.
When you multiply two terms by two terms, you should get four terms. Why is the final result when you multiply two binomials sometimes only three terms? Give an example of how your final result can end up with only two terms.
Answer:
Often when you multiply two binomials, each has a term with the same variable, say x, and two of the terms combine to make one single x – term. If the two terms combine to make zero, there will be only two of the four terms left. For example, (x + 3)(x – 3) = x2 – 9.