Before recalling about Decimal Fraction let us learn the fundamentals of what is a fraction. A fraction is formed up of two parts namely numerator and denominator. A Decimal Fraction is a Fraction having a denominator of 10 or multiples of 10 such as 100, 1000, 10000, …., etc. This article helps you to be well versed with Decimals Fractions such as Definitions, Facts, Operations performed on Decimal Fractions, Solved Examples.
What is a Decimal Fraction?
A Decimal Fraction is a Fraction in which the denominator is a power of 10 such as 10, 100, 1000, etc. You can write Decimal Fractions with a Decimal Point instead of a Denominator. By expressing the decimal fractions using decimal point calculations of addition, subtraction, multiplication, and division will be much simpler.
Examples:
\(\frac { 13 }{ 100 } \) = 0.13
\(\frac { 54 }{ 10 } \) = 5.4
Also, See:
Operations on Decimal Fractions
Addition and Subtraction of Decimal Fractions: Given Numbers are placed under each other so that the decimal points lie in each column and below one another. Later, the numbers are added and subtracted in a regular way.
For Example:
Add 0.0045 and 3.0423
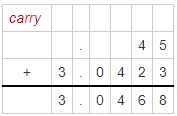
The Sum of 0.0045 and 3.0423 is 3.0468
Multiplication of Decimal Fractions: Multiply the given numbers without considering the decimal point. After that, the decimal point is marked off to obtain the decimal places that is the sum of decimal places in the given numbers.
For Example 0.3*0.03*0.003
Multiply the numbers without considering the decimal point
3*3*3 = 27
Now find the number of decimal places to be marked by adding the decimal places in the given numbers i.e. (1+2+3) = 6 i.e. 0.000027
Dividing Decimal Fraction by a Counting Number: Divide the given number without considering the decimal point by counting the number. Later, after obtaining the quotient place as many decimal places are there in the dividend. If we were to divide 0.0028÷7 we will firstly divide 28÷7 and the quotient is 4. As there are 4 decimal places in the given number place the same in quotient obtained i.e. 0.0004
Thus, 0.0028÷7 = 0.0004
Dividing Decimal Fraction by a Decimal Fraction: Multiply both the dividend and divisor with suitable powers of 10 so that you can make them as a whole number and then proceed.
Thus, \(\frac { 0.00077 }{ 0.11 } \) = \(\frac { 0.00077*100 }{ 0.11*100 } \)
= \(\frac { 0.077 }{ 11 } \)
= 0.007
Solved Examples on Decimal Fractions
1. Convert (i) 0.60 and (ii) 4.008 into vulgar fractions?
Solution:
(i) 0.60 = \(\frac { 60 }{ 100 } \) = \(\frac { 3 }{ 5 } \)
(ii) 4.008 = \(\frac { 4008 }{ 1000 } \) = \(\frac { 501 }{ 125 } \)
In order to convert decimal into vulgar fractions firstly place 1 in the denominator and annex with as many zeros as the number of digits after the decimal point in the given number. Later, remove the decimal point and note the whole number in the numerator. Reduce it to Lowest Form. Remember Annexing Zeros to the Right of Decimal Fraction doesn’t change the value.
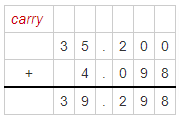
2. Add 35.2 + 4.098?
Solution:
Given Numbers are placed under each other so that the decimal point lies in one column. Numbers can be subtracted or added in a usual way.
3. Evaluate i) 5.3029×100
Solution:
i) 5.3029×100
To Multiply a Decimal Fraction by a Power of 10 shift the decimal point to the right as many places of decimal that is to the power of 10.
5.3029×100 = 530.29
4. Find the product
i) 2.232×0.1
Simply multiply the numbers without considering the decimal point. i.e. 2232*1= 2232
Later, count the number of decimal places in the given numbers i.e. (3+1) = 4
Now put the decimal after 4 that counts 4 digits from right thus 0.02232
5. Evaluate 0.81÷ 9?
Solution:
Divide the given number as if there is no decimal point. 81÷9 = 9
After obtaining the quotient count the number of decimal places in the given number i.e. 0.81 =2
Hence place the decimal point on the left of 0.09
