In Maths Numbers are Classified into Various Types like Real Numbers, Whole Numbers, Natural Numbers, Rational Numbers, etc. Decimal Numbers is a Standard form among them used to represent integers and non-integer numbers. By going through this article, you will learn all about the Definition of Decimals, Types, Properties, Conversions, Examples, etc. in the later modules.
What are Decimals?
Decimals are one type of numbers that has a whole number and fractional part separated by a decimal point. The Dot present between the whole number part and fractional part is called the decimal point.
For instance, 23.4 is a decimal number in which 23 is a whole number and 4 is called the fractional part.
“.” is called the decimal point.
List of Decimal Concepts
Below is the list of Decimal Topics for your reference. You can access them by simply clicking on the quick links available. Once you click on them you will be redirected to a new page having the entire concept explained with examples. Try solving as much as possible to get a good grip on the concept.
- Decimal Numbers
- Decimal Fractions
- Decimal Places
- Decimal and Fractional Expansion
- Like and Unlike Decimals
- Conversion of Unlike Decimals to Like Decimals
- Comparing Decimals
- Adding Decimals
- Subtracting Decimals
- Simplify Decimals Involving Addition and Subtraction Decimals
- Multiplying Decimal by a Whole Number
- Multiplying Decimal by a Decimal Number
- Dividing Decimal by a Whole Number
- Dividing Decimal by a Decimal Number
- Simplification of Decimal
- Converting Decimals to Fractions
- Converting Fractions to Decimals
- Rounding Decimals
- Rounding Decimals to the Nearest Whole Number
- Rounding Decimals to the Nearest Tenths
- Rounding Decimals to the Nearest Hundredths
- Round a Decimal
- H.C.F. and L.C.M. of Decimals
- Terminating Decimal
- Non-Terminating Decimal
- Repeating or Recurring Decimal
- Pure Recurring Decimal
- Mixed Recurring Decimal
- Conversion of Pure Recurring Decimal into Vulgar Fraction
- Conversion of Mixed Recurring Decimals into Vulgar Fractions
Types of Decimal Numbers
Decimal Numbers are classified into two types namely
- Recurring Decimal Numbers
- Non-Recurring Decimal Numbers
- Decimal Fraction
Recurring Decimal Numbers: These are also called Repeating or Non-Terminating Decimals. These Recurring Decimals are further classified into Finite and Infinite.
Example:
3.2525(Finite)
4.12121212……(Infinite)
Non-Recurring Decimal Numbers: These are also called Non-Repeating or Terminating Decimals. They are further classified into finite and infinite non-recurring decimal numbers.
Example:
5.2475 (Finite)
4.1367254….(Infinite)
Decimal Fraction: It Represents the fraction whose denominator is in powers of ten.
31.75 = 3175/100
22.415 = 22415/1000
In Order to Change the Decimal Number to Decimal Fraction firstly place 1 in the denominator and remove the decimal point. “1” is followed by zeros that are equal to the number of digits following the decimal point.
For Example to convert 2.345 to decimal fraction we get
22.345 = 2345/1000
2 represents the power of 101 that is the tenths position.
2 represents the power of 100 that is the unit’s position.
3 represents the power of 10-1 that is the one-tenth position.
4 represents the power of 10-2 that is the one-hundredths position.
5 represents the power of 10-3 that is the one-thousandths position
This is how each digit is represented to the power of a decimal number.
Place Value in Decimals
Place Value System defines the position of a digit in a number that helps to determine its value. When we write Numbers Position of each digit is important.
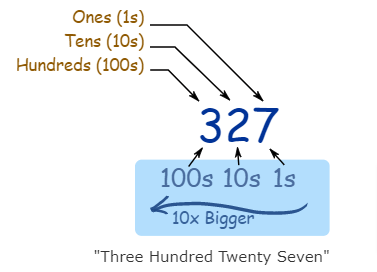
The position of “7” is in One’s place, which means 7 ones (i.e. 6).
The position of “2” is in the Ten’s place, which means 2 tens (i.e. twenty).
The position of “3” is in the Hundred’s place, which means 3 hundred.
As we go left, each position becomes ten times greater.
Therefore, we read it as Three Hundred Twenty-Seven
On Moving towards the left each position becomes 10 times bigger and
Tens are 10 times bigger than ones and similarly, Hundreds are 10 times bigger than Tens.
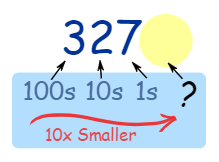
Moving towards the right each position becomes 10 times smaller from Hundreds to Tens to Ones. If we continue further the process after ones \(\frac { 1 }{ 10 } \)ths are smaller. Before doing so, you need to place a decimal point.

Place Value Chart
For a better understanding of the concept of place value check out the Place Value Chart below.
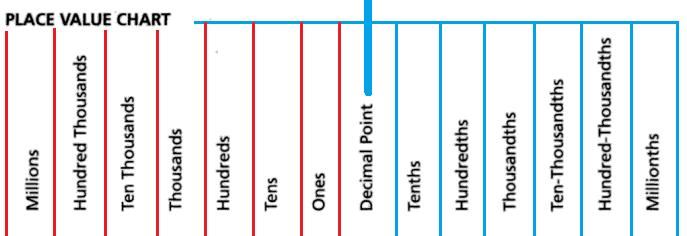
Digits to the left of the decimal point are multiplied with positive powers of 10 in increasing order from right to left. In the same way, digits to the right of the decimal point are multiplied with negative powers of 10 in increasing order from left to right.
Example:
71.325
Decimal Expansion of the number is expressed as follows
{(7*10)+(1*1)} + {(3*0.1)+(2*0.01)+(5*0.001)}
Here, each number is multiplied with associated power of 10.
Decimals Properties
Below is the list of important properties of decimal numbers under both multiplication and division operations. They are as follows
- Irrespective of the decimal numbers multiplied in any order the product remains unchanged.
- On multiplying a whole number and decimal number in any order the product remains the same.
- If a decimal fraction is multiplied by 1 product is the decimal fraction itself.
- If you multiply a decimal fraction with zero the product is zero(0).
- On dividing a decimal number with 1, the quotient is the decimal number itself.
- If you divide a decimal number with the same number the quotient is 1.
- If you divide 0 with any decimal the quotient becomes zero.
- Division of a Decimal Number with 0 isn’t possible since the reciprocal of 0 doesn’t exist.
Arithmetic Operations on Decimals
Similar to performing Arithmetic Operations on Integers you can do the same with Decimals. Let us discuss important tips while performing arithmetic operations.
Addition: In Decimal Numbers Addition, line up the decimal points of given numbers and then add the numbers. If you don’t find the decimal point, the decimal is behind the number.
Subtraction: Decimal Subtraction is also similar to Decimal Addition. Just like Decimal Addition line up the decimal point of given numbers and subtract the values. To do the arithmetic operation use place holding zeros for your reference.
Multiplication: While Performing Multiplication of Decimal Numbers multiply similar to integers as if the decimal point is not present. Find the product and count the number of digits next to the decimal point in both the numbers. Count indicates how many numbers are needed after the decimal point in the product value.
Division: In Order to divide decimal numbers firstly move the digits so that the number becomes whole numbers. Perform Division Operation similar to Integers Division.
Decimal to Fraction Conversions
Conversion of Fraction to Decimal or Decimal to Fraction is quite simple. We have explained both the methods by even taking few examples. They are as follows
Decimal to Fraction Conversion
Numbers after the decimal points denotes tenths, hundredths, thousandths, and so on. While converting from decimal to fraction note down the decimal numbers in expanded form and then simplify the values.
Example 0.45
Expanded form of 0.45 is 45*(\(\frac { 1 }{ 100 } \)) = \(\frac { 45 }{ 100 } \) = \(\frac { 9 }{ 20 } \)
Fraction to Decimal Conversion
In order to change from fraction to decimal simply divide the numerator with the denominator
For example, \(\frac { 9 }{ 2 } \) is a fraction. If it’s divided, we get 4.5
Problems on Decimals
Question 1.
Convert \(\frac { 15 }{ 10 } \) to decimal?
Solution:
To change from fraction to decimal you just need to divide the numerator with the denominator
On dividing, we get the decimal value as 1.5
Question 2.
Express 3.35 in fraction form?
Solution:
The given decimal number is 3.35
The expanded form of 3.35 is
= 335 x (\(\frac { 1 }{ 100 } \))
= \(\frac { 335 }{ 100 } \)
=\(\frac { 67 }{ 20 } \)
Hence, the equivalent fraction for 3.35is \(\frac { 67 }{ 20 } \).
