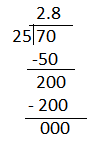Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 7 Module 2 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Student Book Answer Key Unit 7 Module 2
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 2 Session 1 Answer Key
Story Problems
Solve each problem. Show your work. Write an equation to represent the problem and the solution.
Question 1.
Trading cards come in packs of 12 cards. Chris bought 300 cards. How many packs did he buy?
Answer:
Given that trading cards come in packs of 12 cards and Chris bought 300 cards.
To get the number of packs he bought, divide 300 by 2, 300÷12=25
Thus he bought 25 packs.
Question 2.
Chris dealt out all the trading cards to himself and 11 friends so they could play a game. How many cards did each person get?
Answer:
Given that Chris dealt out all the trading cards to himself and 11 friends so they could play a game.
To get the number of cards each will get, divide 300 by 2, 300÷12=25.
Each person will get 25 cards.
Question 3.
Anna earned $270 over the summer by mowing lawns. 1f she mowed 18 lawns and earned the same amount each time, how much did Anna earn per lawn?
Answer:
Given that Anna earned $270 over the summer by mowing lawns and she mowed 18 lawns.
To calculate the earnings per lawn, divide 270 by 18, 270÷18=15
Anna will earn $15 per lawn.
Question 4.
Mr. Foley is setting up chairs for a meeting. Each row has 18 chairs. 270 people are expected to come to the meeting. How many rows of chairs should he set up?
Answer:
Given that Mr. Foley is setting up chairs for a meeting. Each row has 18 chairs. 270 people are expected to come to the meeting.
To calculate the number of rows to be set up, divide 270 by 18, 270÷18=15.
He needs to set up 15 rows of chairs.
Question 5.
There is \(\frac{1}{2}\) of a pan of lasagna to feed Marta and her three cousins. How much of the whole pan of lasagna do they each get?
Answer:
Given that there is \(\frac{1}{2}\) of a pan of lasagna to feed Marta and her three cousins.
So, all the four people willl get \(\frac{1}{4}\) × \(\frac{1}{2}\) = \(\frac{1}{8}\)
Ecah will get \(\frac{1}{8}\) of lasagna.
Question 6.
Marta has 4 cups of grated cheese. She needs \(\frac{1}{2}\) a cup of cheese for each mini-pizza. How many mini-pizzas can she make?
Answer:
Given that Marta has 4 cups of grated cheese and she needs \(\frac{1}{2}\) a cup of cheese for each mini-pizza.
She can make, 4 ÷ \(\frac{1}{2}\) = 8
So, in total 8 mini-pizza can be made with 4 cups of grated cheese.
Question 7.
CHALLENGE Craig is organizing a neighborhood party for his scout troop. He needs to deliver fliers to all of the houses in the neighborhood. There are 13 streets with 12 houses, 14 streets with 11 houses, and 8 streets with 13 houses. If there are 18 boys in his scout troop helping Craig deliver the fliers, how many fliers should each pair of boys get?
NOTE The group of 18 boys who will be working in pairs to deliver the fliers does not include Craig, because he will be busy keeping everyone organized.
Answer:
Given that there are 13 streets with 12 houses, 14 streets with 11 houses, and 8 streets with 13 house and 18 boys to deliver the fliers.
Each pair of boys means 2 boys. Therefore, there will be 9 pair of boys.
Total number of houses will be 12+11+13 = 36
Total number of streets will be 13+14+8 = 35
To calculate the number of fliers each boys will get, divide the number of houses by number of boys.
36 ÷ 18 = 2
Each pair of boys will get 2 fliers.
Thinking About Money
Ebony was putting her loose change into rolls to take to the bank.
Question 1.
Ebony discovered she had $8 in quarters.
a. How many quarters are there in $8?
Answer:
$8 ÷ \(\frac{1}{4}\) = 32
b. Choose the division expression you would use to find the number of quarters in $8.
(A) $8 ÷ 4
(B) $8 ÷ \(\frac{1}{4}\)
(C) $8 ÷ \(\frac{1}{2}\)
Answer:
The correct expression to find the number of quarters in $8 will be $8 ÷ \(\frac{1}{4}\)
So, the correct option will be B.
Question 2.
Ebony had $6 in dimes.
a. How many dimes are in $6?
Answer:
One dollar equals to 10 dimes.
Therefore, $6 will have 6×10 = 60 dimes.
b. Write the division expression you would use to find the number of dimes in $6.
Answer:
The division expression to find the number of dimes in $6 will be $6 ÷ \(\frac{1}{10}\)
Question 3.
Ebony also had $6 in nickels.
a. How many nickels are in $6?
Answer:
1 dollar equals to 20 nickles.
So, $6 will have 6×20 = 120 nickels.
b. Write the division expression you would use to find the number of nickels in $6.
Answer:
The division expression to find the number of nickels in $6 will be $6 ÷ \(\frac{1}{20}\)
Question 4.
Ebony deposited $64.32 when she went to the bank. If she already had $487.99 in her account, what it her new balance (total)? Show your work.
Answer:
Given that Ebony deposited $64.32 when she went to the bank. If she already had $487.99 in her account.
In total her new balance will sum of the money she deposited and the amount she had earlier in her account.
$64.32 + $487.99 = $552.31
She will have $552.31 in total.
Question 5.
How much more does Ebony need to reach her goal of $1,000.00 in her account? Show your work.
Answer:
To reach $1,000.00, subtract the amount she had in her account from $1,000.00.
She had $552.31 in total in bher account.
So, $1,000.00 – $552.31 = $447.69
She will need $447.69 to reach her goal of $1,000.00 in her account.
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 2 Session 2 Answer Key
Multiplication Round & Check
Question 1.
Multiply the numbers.
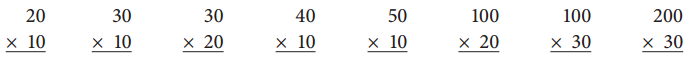
Answer:
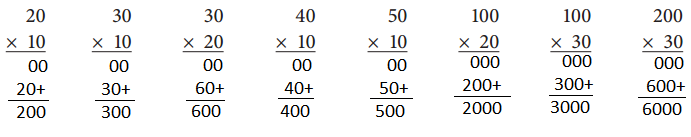
20 × 10 = 200
30 × 10 = 300
30 × 20 = 600
40 × 10 = 400
50 × 10 = 500
100 × 20 = 2000
100 × 30 = 3000
200 × 30 = 6000
Question 2.
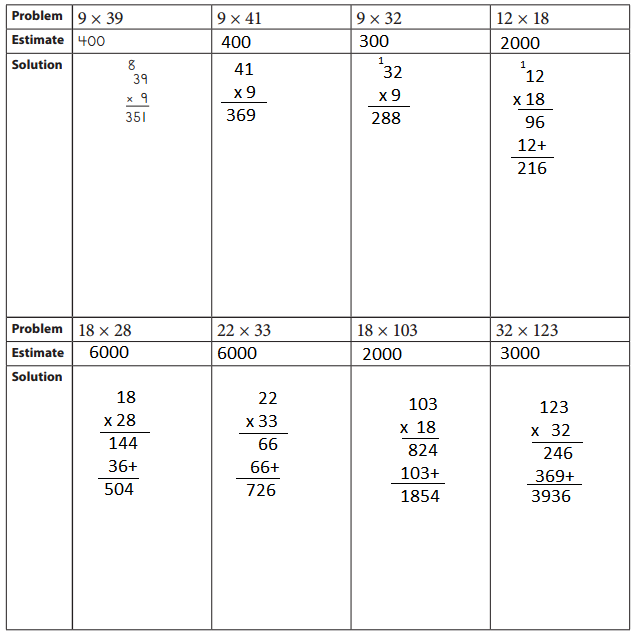
Think about rounding to estimate the answers to the problems below. Then rewrite each problem vertically and solve it using the standard algorithm.
Hint: Use the answers above to help with your estimates.
Answer:
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 2 Session 3 Answer Key
Work Place Instructions 7B Quotients Race to One Hundred
Each pair of players needs:
- math journals
- 1 deck of Number Cards, wild cards removed
- 1 Quotients Race to One Hundred Record Sheet to share
1. Players decide who will be the dealer and who will go first. The dealer gives 5 cards to each player.
2. Player 1 arranges her 5 cards so that 2 cards form a divisor and 3 cards form a dividend. Then, Player 1 writes the division problem in the Problem column on her side of the record sheet.
Players need to think strategically about how to arrange the cards to produce the greatest quotient possible.
Player 1 I drew 9, 6, 4, 3, and 7. think I’ll try 976 and 34, so my problem is 976 ÷ 34.
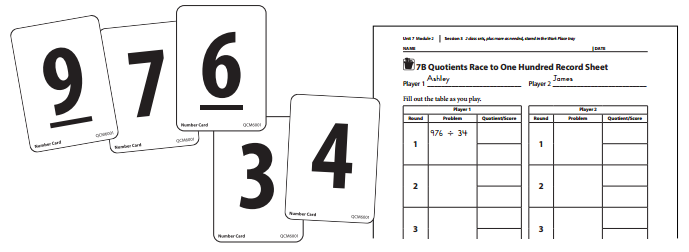
3. Player 1 works in her math journal to solve the division problem formed by the cards. She can disregard any remainder.
4. Player 1 shows her work to Player 2 and Player 2 says whether he agrees with the quotient.
- If Player 2 agrees with the quotient, Player 1 records the whole number portion of the quotient in the Quotient/Score column on the record sheet.
- If Player 2 disagrees with the quotient, the two players rework the problem together. Then, Player 1 records the whole number part of the quotient in the Quotient/Score column on the record sheet.
Player 1 I made a ratio table for 34, and subtracted off the amounts, like this.
Player 2 I agree with your work, so you can put 28 for your first quotient.
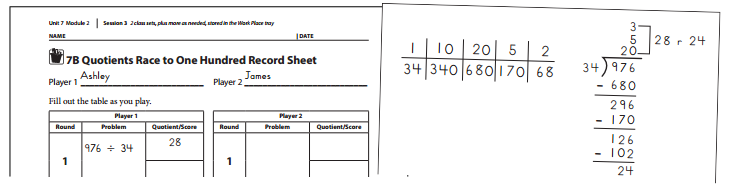
5. Player 2 takes a turn.
6. Players continue to take turns. After each turn, a player records her newest quotient, adds that quotient to her previous quotie3nts to get her new score, and records her new score. The player whose quotients total 100 or more first is the winner.
Game Variations
A. Players can play individually and see how many turns it takes them to get to 100, or they can play together, supporting each other as they see how many turn it takes them to get to 100.
B. Players can deal out 6 cards and make 4-digit dividends.
C. Players can play Remainders Race to 3. In this version, players find the remainder in each division problem and record the remainder as a fraction. As they play, they add the remainders instead of the whole number quotients. The first player who gets a total of 3 wins the game.
D. If players need more practice with 1-digit divisors, they can deal 3 or 4 cards and arrange the problem so there is a 1-digit divisor and a 2- or 3-digit dividend.
E. Players can add the wild cards to the deck of Number Cards and, upon receiving a wild card, choose a number for that card to represent.
Answer:
Player 2 is the winner.

Dividing Fractions & Whole Numbers
Question 1.
Fill in the bubble to show what each expression below means. Then use labeled sketches and numbers to model and solve each problem. Show your work and remember to write the answer at the bottom of each box.
4 ÷ \(\frac{1}{5}\)
![]() How many groups of 4 are there in \(\frac{1}{5}\)?
How many groups of 4 are there in \(\frac{1}{5}\)?
![]() How many groups of \(\frac{1}{5}\) are there in 4?
How many groups of \(\frac{1}{5}\) are there in 4?
![]() What is \(\frac{1}{5}\) of 4?
What is \(\frac{1}{5}\) of 4?
Answer:
Groups of 4 in \(\frac{1}{5}\) will be, \(\frac{1}{5}\) × 4 = \(\frac{4}{5}\)
Groups of \(\frac{1}{5}\) in 4 will be, 4 ÷ \(\frac{1}{5}\) = 20
\(\frac{1}{5}\) of 4 = \(\frac{1}{5}\) × 4 = \(\frac{4}{5}\)
\(\frac{1}{2}\) ÷ 4
![]() How many groups of \(\frac{1}{2}\) are there in 4?
How many groups of \(\frac{1}{2}\) are there in 4?
![]() What is \(\frac{1}{2}\) of 4?
What is \(\frac{1}{2}\) of 4?
![]() If you split \(\frac{1}{2}\) into 4 equal shares, how big is each share?
If you split \(\frac{1}{2}\) into 4 equal shares, how big is each share?
Answer:
Groups of \(\frac{1}{2}\) in 4 will be, 4 × \(\frac{1}{2}\) = 2
\(\frac{1}{2}\) of 4 = \(\frac{1}{2}\) × 4 = \(\frac{4}{2}\) = 2
If \(\frac{1}{2}\) is split into 4 equal shares, it will be, \(\frac{1}{2}\) ÷ 4 = \(\frac{1}{8}\)
Question 2.
Mr. Ortega had \(\frac{1}{2}\) of a box of felt markers. He divided the box equally among 3 small groups of students. What fraction of the box of felt markers did each group get?
a. Choose the expression that best represents this problem.
![]() \(\frac{1}{2}\) ÷ 3
\(\frac{1}{2}\) ÷ 3
![]() 3 ÷ \(\frac{1}{2}\)
3 ÷ \(\frac{1}{2}\)
![]() \(\frac{1}{2}\) × 3
\(\frac{1}{2}\) × 3
Answer:
Given that Mr. Ortega had \(\frac{1}{2}\) of a box of felt markers. He divided the box equally among 3 small groups of students.
The fraction of the box of felt markers each group will get, will be \(\frac{1}{2}\) ÷ 3 = \(\frac{1}{6}\)
Therefore, the given expression will be \(\frac{1}{2}\) ÷ 3
b. Solve the problem. Show your work.
Each group of students got ______________ of a box of felt markers.
Answer:
Each group of students will get \(\frac{1}{6}\) of a box of felt markers.
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 2 Session 4 Answer Key
Dividing Marbles
Question 1.
Peter has 320 marbles. He is going to divide them into 32 bags. How many marbles will be in each bag?
a. Write an equation for the problem.
Answer:
Given that Peter has 320 marbles. He is going to divide them into 32 bags.
The expression will be 320÷32 = 10
10 marbles will be there in ecah bag.
b. Solve the problem. Show your work.
Answer:
320÷32 = 10
10 marbles will be there in ecah bag.
Question 2.
Sophia has 352 marbles. She is also going to divide them into 32 bags. How many marbles will be in each bag?
a. Write an equation for the problem.
Answer:
Given that Sophia has 352 marbles. She is also going to divide them into 32 bags.
The equation will be 352÷32 = 11
b. Solve the problem. Show your work.
Answer:
352÷32 = 11
11 marbles will be there in each bag.
Question 3.
Cole has 288 marbles. He is also going to divide them into 32 bags. How many marbles will be in each bag?
a. Write an equation for the problem.
Answer:
Given that Cole has 288 marbles. He is also going to divide them into 32 bags.
The equation will be 288÷32 = 9
b. Solve the problem. Show your work.
Answer:
288÷32 = 9
9 marbles will be there in each bag.
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 2 Session 5 Answer Key
Dealing with Remainders
Question 1.
A bakery donated 273 cookies for the end of the year fifth grade school party. How- many cookies does each of the 84 students get if they share the cookies fairly?
a. Solve the problem. Show your work.
Answer:
Given that a bakery donated 273 cookies for the end of the year fifth grade school party which has 84 students.
To get the sharfe of cookies, divide the cookies with the number of students.
b. Write an equation to represent the problem and the answer.
Answer:
Divide 273 with 84, 273÷84.
c. Explain what you did with the remainder, if any, and why.
Answer:
The remainder will be 21.
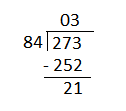
With the remainder 21, expand the quotient to get the remainder 0.
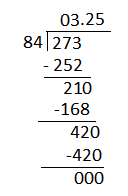
Question 2.
There are 814 students going on a field trip, and they have 31 buses. How many students should go on each bus if they split up evenly on the buses?
a. Solve the problem. Show your work.
Answer:
Given that there are 814 students going on a field trip, and they have 31 buses.
To get the number of students after splitting them evenly, divide the number of students by number of buses.
b. Write an equation to represent the problem and the answer.
Answer:
The equation for above scenario will be 814 ÷ 31
c. Explain what you did with the remainder, if any, and why.
Answer:
With the remainder, expand the quotient, it is non terminating remainder.
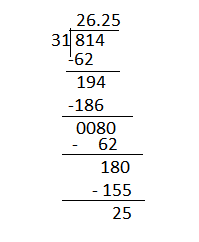
Question 3.
Green Lake School is serving cake to their 840 students on the last day of school. Each large cake serves 48 students. How many cakes does the school need?
a. Solve the problem. Show your work.
Answer:
Given that Green Lake School is serving cake to their 840 students on the last day of school. Each large cake serves 48 students.
To get the count of cakes, divide the students by number of serving.
b. Write an equation to represent the problem and the answer.
Answer:
The equation to represent above problem will be 840÷48
c. Explain what you did with the remainder, if any, and why.
Answer:
840÷48 will give 17.5
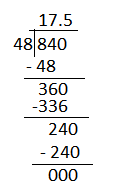
Question 4.
Green Lake school wants to improve the landscaping around the school. The principal collected $476 from 56 parents to plant new trees. If all of the parents donated the same amount, how much did they each give?
a. Solve the problem. Show your work.
Answer:
Given that Green Lake school wants to improve the landscaping around the school. The principal collected $476 from 56 parents to plant new trees and if all of the parents donated the same amount, then each would have given
To get the amount each would given, divide the total amount by the number of parents.
b. Write an equation to represent the problem and the answer.
Answer:
An equation to represent the problem and the answer will be, 476÷56
c. Explain what you did with the remainder, if any, and why.
Answer:
Dividing the 476 by 56 will give 8.5
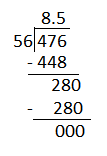
Question 5.
During a play, 744 students will sit in rows in the auditorium. If each row can seat 32 students, how many rows do they need?
a. Solve the problem. Show your work.
Answer:
Given that during a play, 744 students will sit in rows in the auditorium. If each row can seat 32 students.
To get the number of rows, divide the number of students by number students who can sit in one row.
b. Write an equation to represent the problem and the answer.
Answer:
An equation to represent the problem will be 744÷32
c. Explain what you did with the remainder, if any, and why.
Answer:
Dividing 744 by 32 will give 23.25 quotient and 0 as remainder.
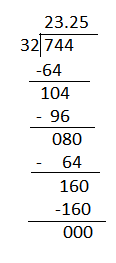
Question 6.
CHALLENGE The Friends and Family Committee sold tickets for a school dance. They used the money to pay for music, decorations, and snacks. Tickets cost $4.50, and 259 students bought tickets. The committee spent \(\frac{1}{3}\) of the money they made on food. They bought 15 platters of food. How much did each platter cost?
a. Solve the problem. Show your work.
Answer:
Given that the Friends and Family Committee sold tickets for a school dance. They used the money to pay for music, decorations, and snacks. Tickets cost $4.50, and 259 students bought tickets.
Total money will be 4.50 × 259 = $1165.5
The committee spent \(\frac{1}{3}\) of the money they made on food, \(\frac{1}{3}\) × 1165.5, which will be 388.5
They bought 15 platters of food, 388.5÷15 = 25.9
Each platter will cost $25.9
b. Write an equation to represent the problem and the answer.
Answer:
An equation to represent the problem and the answer will be 388.5÷15 = 25.9
c. Explain what you did with the remainder, if any, and why.
Answer:
Dividing 388.5 will give 25.9
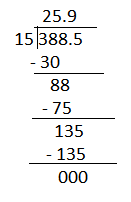 f
f
Story Problems: Division with Remainders
Solve each problem below. Show your work. Use the context of each story to help you decide what to do with the remainder.
Question 1.
The entire Harrisville Middle School is taking a field trip to the symphony. All 282 people will ride the subway to the theater. Each subway has 8 subway cars. If an equal number of people ride in each subway car, how many people will ride in each?
Answer:
Given that the entire Harrisville Middle School is taking a field trip to the symphony. All 282 people will ride the subway to the theater. Each subway has 8 subway cars. If an equal number of people ride in each subway cars, the number of people will ride can be calculated by dividing the total people by subway cars.
282 ÷ 8 = 35.25
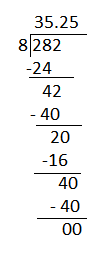
Question 2.
Mrs. Smith’s class has 24 students. The tickets for her class cost $162. How much did each student’s ticket cost? (Teachers get free tickets.)
Answer:
Given that Mrs. Smith’s class has 24 students. The tickets for her class cost $162.
Cost of each ticket can be calculated by dividing 162 with 24
162 ÷ 24 = 6.75
Each student’s ticket cost will be $6.75
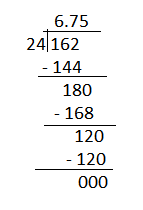
Question 3.
Olivia made brownies for Mrs. Smith’s class. She made 30 brownies and divided the brownies evenly. How many brownies will each student get? (Mrs. Smith says she doesn’t want any.)
Answer:
Given that Olivia made brownies for Mrs. Smith’s class. She made 30 brownies and divided the brownies evenly.
To calculate the number of brownies each student will get, divide 30 by 24.
Each student will get 1.25 brownie.
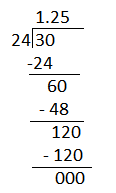
Question 4.
Olivia wants Mrs. Smith to have an equal portion of brownies as well (to take home to her niece). Now how many brownies will each person get?
Answer:
Given that Olivia wants Mrs. Smith to have an equal portion of brownies as well (to take home to her niece).
So now divide 30 by 25.
each person will give 1.2 brownie
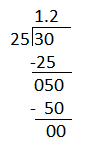
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 2 Session 6 Answer Key
Division Practice
Question 1.
Mr. Lee’s classroom has 966 markers. His 28 students need to share the markers equally so everyone can work on an art project. How many markers should each student get?
a. Solve the problem. Show your work.
Answer:
Given that Mr. Lee’s classroom has 966 markers. His 28 students need to share the markers equally. To calculate the mumber of markers each student will get divide the markers by number of students.
966 ÷ 28 = 34.5
Each student will get 34 markers.
b. Between which two whole numbers does your answer lie? ____________ and _______________
Answer:
The answer will lie between 34 and 35.
c. Write an equation to represent the problem and the answer.
Answer:
An equation to represent the problem will be 966 ÷ 28
d. Explain what you did with the remainder, if any, and why.
Answer:
Dividing 966 by 28 will give 34.5
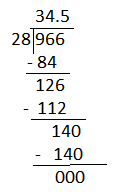
Question 2.
Mr. Lee brought 70 granola bars for his students to share. Three students were absent. How many granola bars can each of his 25 students have?
a. Solve the problem. Show your work.
Answer:
Given that Mr. Lee brought 70 granola bars for his 25 students to share.
b. Between which two whole numbers does your answer lie? ____________ and ____________
Answer:
The obtained answer will lie between 2 and 3.
c. Write an equation to represent the problem and the answer.
Answer:
The equation to represent the problem and the answer will be 70 ÷ 25
d. Explain what you did with the remainder, if any, and why.
Answer:
Dividng 70 by 25 will give 2.8