Students looking for the Bridges in Mathematics Grade 5 Student Book Answer Key Unit 7 Module 1 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Student Book Answer Key Unit 7 Module 1
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 1 Session 1 Answer Key
Rob’s Review
Question 1.
Rob was solving multiplication problems. Write an expression with parentheses to record his thinking for each of the two problems below.
a. Rob solved 97 × 50 by multiplying 100 by 50 and then removing 3 groups of 50.
Answer:
Given that
97 × 50 = (100-3)×50
97 × 50 = (100×50)-(3×50)
b. Rob solved 25 × 44 by finding \(\frac{1}{4}\) of 44 and then multiplying by 100.
Answer:
25 × 44 = \(\frac{1}{4}\) × 44 × 100
Question 2.
Evaluate Rob’s two expressions.
a.
b.
Answer:
a. 97 × 50 = (100×50)-(3×50)
4850 = 5000-150
4850 = 4850
b. 25 × 44 = \(\frac{1}{4}\) × 44 × 100
1100 = \(\frac{44}{4}\) × 100
1100 = 11×100
1100 = 1100
Question 3.
Rob saw a friend use the standard algorithm to solve the problem 290 × 14.
a. Solve the problem using the standard algorithm.
Answer:
= 290 × 14
= (300-10) × 14
= (300-10) × 14
= 300×14 – 10×14
= 4200 – 140
= 4060
b. Rob said he thought there was a more efficient way to solve this problem, and suggested his friend use the ratio table below. Fill in Rob’s ratio table.

Answer:
The ratio for 1 is 4.
Therefore for 2, it will be 2×14=48
Ratio for 3 will be, 3×14=42
Ratio for 300 will be, 300×14=4200
Ratio for 10 will be, 10×14=140
Ratio for 290 will be, 290×14=4060

Bridges in Mathematics Grade 5 Student Book Unit 7 Module 1 Session 2 Answer Key
Array Work
Fill in the blanks on each array. Then write two equations—one multiplication, and one division—equation, to match the array.
Question 1.
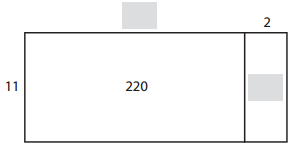
______________ × _______________ = ______________
______________ ÷ _______________ = ______________
Answer:
The multiplication equation will be,
11 × 20 = 220
The division equation will be,
22 ÷ 11 = 2
Question 2.
______________ × _______________ = ______________
______________ ÷ _______________ = ______________
Answer:
The multiplication equation will be,
2\(\frac{1}{2}\) = \(\frac{5}{2}\)
3× \(\frac{5}{2}\) = \(\frac{15}{2}\) or 7 \(\frac{1}{2}\)
The division equation will be,
1\(\frac{1}{4}\) ÷ \(\frac{1}{2}\) = 2\(\frac{1}{2}\)
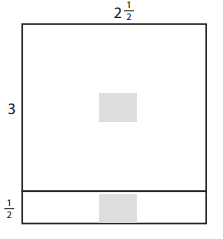
Question 3.
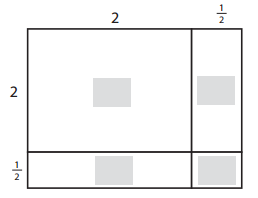
______________ × _______________ = ______________
______________ ÷ _______________ = ______________
Answer:
The multiplication equation will be,
2 × 2 = 4
The division equation will be,
2 ÷ \(\frac{1}{2}\) = 1
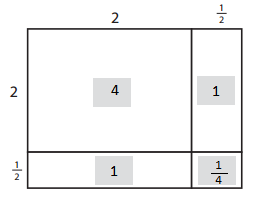
Question 4.
______________ × _______________ = ______________
______________ ÷ _______________ = ______________
Answer:
11 × 30 = 330
33 ÷ 11 = 3
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 1 Session 3 Answer Key
Work Place Instructions 7A Roll Five
Each pair of players needs:
- math journals
- 2 dice numbered 1-6
- 2 dice numbered 4-9
- 1 die numbered 0-5
- 1 Roll Five Record Sheet to share
1. Each player rolls a die numbered either 1-6 or 4-9.
2. The product of the two dice rolled becomes the target number, and both players write the target number on their sides of the record sheet.
3. All five dice are rolled, and players write the digits rolled on their sides of the record sheet.
Note: Both players write the same five digits.
4. Working separately in their math journals, players use any combination of operations (addition, subtraction, multiplication, and/or division) to make an equation that results in the target number.
- Players do not have to use all five digits rolled, but they must make an equation that results in the target number.
- Each digit may be used only once.
- Players keep track of their thinking in their math journals.
5. Players write their equations on the record sheet, using parentheses as necessary. Players check each other’s equations and work for accuracy.
- Players can have different equations; they just need to reach the same target number.
6. Players determine their scores and write them on the record sheet.
- 1 point for each digit used
- 1 additional point for using multi-digit division where the divisor is two or more digits
- 1 additional point for using fractions or decimals
- For example, given 5, 7, 3, 2, 5, and the target number 15, a player could earn an extra point for 375 + 25 = 15.
- Given 5, 6, 5, 5, 1, and the target number 10, a player could earn an extra point for (6 × 5) × 5 + 15 = 10.
- Given 8, 3, 5, 1, 2, and the target number 25, a player could earn an extra point for ((8 × 3) × .5) × 2 + 1 = 25.
- A player who is unable to create an equation for the target number earns zero points for that round.
7. The player with the higher total score after four rounds wins the game.
Game Variations
A. Players work together to create one equation for each round.
B. Players must use all five digits in order for the equation to earn any points.
C. Players use a calculator to help create equations that result in their target number.
Note: Check that the calculator uses the standard order of operations. Enter 1 + 3 × 2. If the answer is 7, that calculator will work for this game.
Answer:
Roll Five & Ratio Tables
Destiny and Jesse are playing Roll Five. They want to add, subtract, multiply and/or divide any of the digits on their five dice to reach their target number.
Question 1.
Destiny’s target number was 24. She rolled the digits 2, 5, 6, 9, and 1.
a. Destiny thinks she can use 6, 2 and 9 to reach her target number. Record an expression she could use with these three digits, and then evaluate the expression.
Answer:
Given that Destiny’s target number was 24. If she uses 6,2 and 9. She can use the below expression to achieve it.
(9×2)+6 = 24
b. What is her score?
Answer:
If she uses 6,2 and 9, then her score will be 24.
c. Jesse encourages Destiny to try for a higher score. Record an equation Destiny could make with 2, 5, 6, 9, and 1 to reach the target number of 24.
Answer:
Given 2, 5, 6, 9, and 1, the target number 24. The equation will be (6 × 1) × 2 + (9 – 5).
d. What is her new score?
Answer:
Her new score will be (6 × 1) × 2 + (9 – 5) = 16
Question 2.
Jesse’s target number was 16. He rolled the digits 3, 4, 4, 6, and 8.
a. Jesse says that 6 times 8 is 48, divided by 3 is 16. Write an expression to record Jesse’s thinking, and then evaluate the expression.
Answer:
6 times 8 in expression will be, 6 × 8. We know that 6 × 8 = 48.
48 divided by 3 in expression will be, 48 ÷ 3. We know that 48 ÷ 3 = 16.
b. Jesse thinks he can get a higher score if he multiplies 6 and 8, divides the product by 4, and then adds 4. Write an expression to record Jesse’s thinking, and then evaluate the expression.
Answer:
6 multiply by 8, 6 × 8 = 48
If 48 is divided by 4, 48 ÷ 4 = 12
(6 × 8) ÷ 4 = 12
12 + 4 = 16
Question 3.
Mariah was solving the problem 342 ÷ 19. She started the ratio table below. Complete the ratio table to find the quotient. Add to Mariah’s ratio table as needed.

342 ÷ 19 = __________________
Answer:
To complete the above table Mariah needs to multiply 19 till 18 times.

342 ÷ 19 = 18
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 1 Session 4 Answer Key
Fruit Pizza
Lisa’s parents own a bakery. They sell fruit pizzas made of granola crust with yogurt filling and one fruit topping. Many fruit topping choices are available.
Lisa wants to make a few fruit pizzas to eat with her friends, and she needs to figure out how much fruit to buy for each kind of pizza she makes. She found a chart that her parents made for their latest pizza order that shows how much of each kind of fruit was used on different numbers of pizzas.
Use the information on the chart below to help Lisa figure out how many cups of fruit she would need for each different kind of pizza, so she can decide if she wants to make a blueberry pizza, a strawberry pizza, a peach pizza, or some of the other kinds on the list.
Note: The cups of fruit are divided evenly among the number of pizzas for that kind of fruit.
Question 1.
Solve each problem in your math journal, and show all of your work. Write your answers on the chart below.
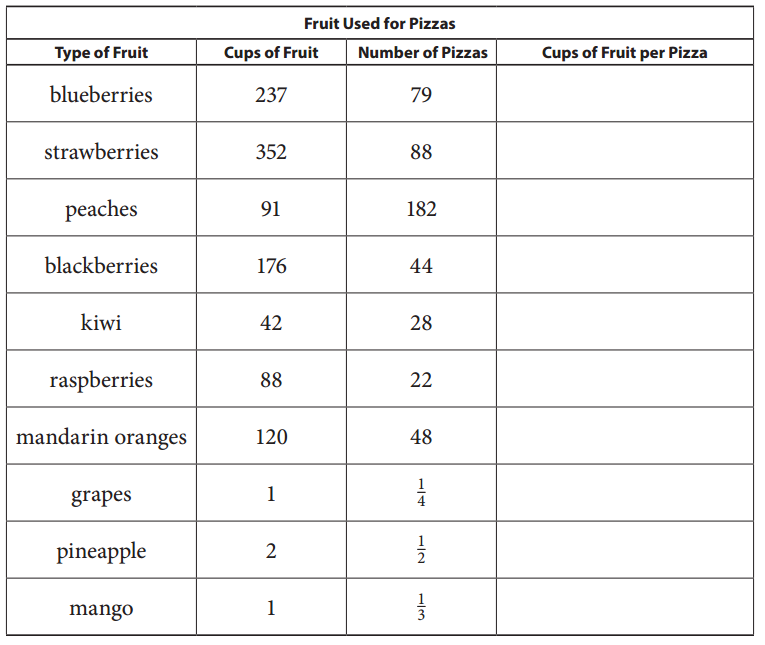
Answer:
Given that 237 cups of blueberries were used to make 79 pizzas. So, the number of cups required per pizza will be 237÷79=3
352 cups of starwberries were used to make 88 pizzas. So, the number of cups required per pizza will be 352÷88=4
91 cups of peaches were used to make 182 pizzas. So, the number of cups required per pizza will be 182÷91=2
176 cups of balckberries were used to make 44 pizzas. So, the number of cups required per pizza will be 176÷44=4
42 cups of kiwi were used to make 28 pizzas. So, the number of cups required per pizza will be 42÷28=1.5
88 cups of raspberries were used to make 22 pizzas. So, the number of cups required per pizza will be 88÷22=4
120 cups of mandarin oranges were used to make 48 pizzas. So, the number of cups required per pizza will be 120÷48=2.5
1 cup of grapes is used to make \(\frac{1}{4}\) pizza. 4 times \(\frac{1}{4}\) will make 1. So, the number of cups required to make 1 pizza will be 4×1=4 cups.
2 cups of pineapple were used to make \(\frac{1}{2}\) pizza. 2 times \(\frac{1}{2}\) will make 1. So, the number of cups required to make 1 pizza will be 2×2=4 cups.
1 cup of mango is used to make \(\frac{1}{3}\) pizza. 3 times \(\frac{1}{3}\) will make 1. So, the number of cups required to make 1 pizza will be 3×1=3 cups.
Thinking About Division
Question 1.
Show your strategy and answer in three ways:
- with a model such as an array or ratio table
- in words
- with an equation
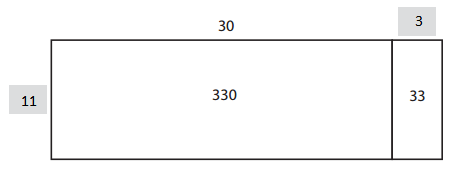
a. How can you use 1100 ÷ 11 to help you find 1089 ÷ 11?
Answer:
1100 ÷ 11 will give 100.
1089 = 1100 – 11
1089 ÷ 11 = (1100-11)÷11
= (1100 ÷ 11) – (11 ÷ 11)
= 100 – 1
= 99
b. How can you use 900 ÷ 9 to help you find 936 ÷ 9?
Answer:
900 ÷ 9 will give 100
936 = 900+36
936 ÷ 9 = (900+36) ÷ 9
= (900÷9) + (36÷9)
= 100 + 4
= 104
Question 2.
Look at the five division problems below. Before you solve them, decide if any of the problems have the same quotient. Explain how you know, and then solve each one.
Answer:
In the given sums below, the quotient for first and third sums will be same.
The quotient for second and fourth sums will be the same.
a. 42 ÷ 7 = _______________
Answer:
42 ÷ 7 will give 6, as we know that 7×6=42.
Here, the quotient will be 6.
b. 420 ÷ 7 = _________________
Answer:
420 ÷ 7 will give 60, as we know that 7×60=420.
Here, the quotient will be 60.
c. 420 ÷ 70 = _________________
Answer:
420 ÷ 70 will give 6, as we know that 70×6=420.
Here, the quotient will be 6.
d. 4,200 ÷ 70 = ________________
Answer:
4200 ÷ 70 will give 60, as we know that 70×60=4200.
Here, the quotient will be 60.
e. 4,620 ÷ 70 = ________________
Answer:
4,620 ÷ 70 = 66, as we know that 70×66=4620.
Here, the quotient will be 66.
Question 3.
Mariana needs to solve the problem 588 ÷ 42. She prefers to think about division as multiplication. She begins by thinking, “I know 10 groups of 42…” Create a ratio table to model Mariana’s thinking and solve the problem.
Answer:

As we know that 42×1=42 and so on.
From the table above, we know that 42×14=588.
Therefore, 588 ÷ 42 will be 14.
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 1 Session 5 Answer Key
Food Project
The Seliwood Community Center wants to donate hot dogs to the Southeast Portland Food Project, and they want to find the best deal.
Question 1.
At Food Mart, hot dogs can be purchased in packages of 8 for $2.40 or packages of 12 for $3.00. Which is a better buy? Explain how you know.
Answer:
Given that at Food Mart, hot dogs can be purchased in packages of 8 for $2.40 or packages of 12 for $3.00.
If packages of 8 is purchased, then the cost of 1 package will be equal to 2.40÷8 = $0.3
If packages of 12 is purchased for $3.00, then the cost of 1 package will be 3.00÷12=$0.25
Therefore, packages of 12 will be the best buy.
Question 2.
At Food World, hot dogs are sold in packages of 24 for $5.76 or packages of 50 for $12.00. Which is a better buy? Explain how you know.
Answer:
Given that at Food World, hot dogs are sold in packages of 24 for $5.76 or packages of 50 for $12.00.
If packages of 24 is purchased for $5.76, then the cost of 1 package will be $0.24
If packages of 50 is purchased for $12.00, then the cost of 1 package will be $0.24
As the cost of 1 package is same for both the cases, both the packages can be bought.
Question 3.
The community center organizers want to buy 600 hot dogs. What will the cost be if they purchase the packages with the best buy? Show your thinking.
Answer:
Given that the community center organizers want to buy 600 hot dogs.
Packages of 50 for $12.00 is the best buy.
The community needs 600 hot dogs, so, 12×50, 12 such packages are to be bought.
The cost will be 12×12= $144.00
Therefore, the cost will be $144.00 if bought with best buy.
Question 4.
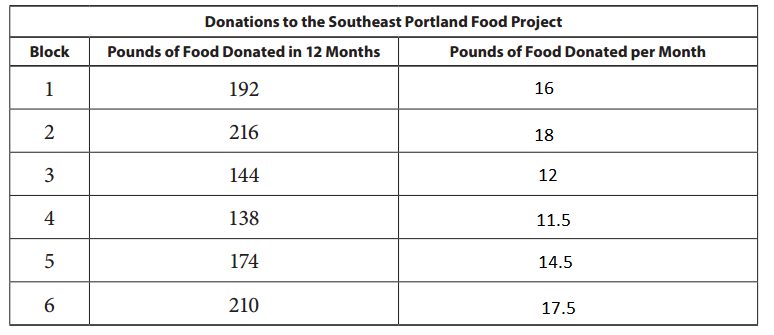
Six blocks of neighbors in Seliwood and Westmoreland donate food to the Southeast Portland Food Project. The table below shows how many pounds of food each block donated during the last 12 months. Fill in the table to show how many pounds of food each block donated per month.
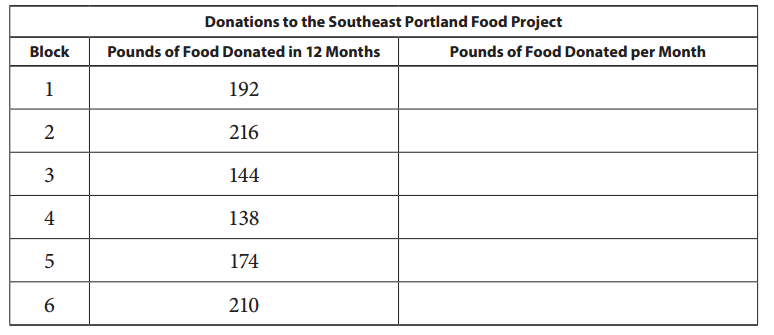
Answer:
If 192 pounds of food is donated in 12 months, then 16 pounds in donated per month.
If 216 pounds of food is donated in 12 months, then 18 pounds in donated per month.
If 144 pounds of food is donated in 12 months, then 12 pounds in donated per month.
If 138 pounds of food is donated in 12 months, then 11.5 pounds in donated per month.
If 174 pounds of food is donated in 12 months, then 14.5 pounds in donated per month.
If 210 pounds of food is donated in 12 months, then 17.5 pounds in donated per month.
Bridges in Mathematics Grade 5 Student Book Unit 7 Module 1 Session 6 Answer Key
Division with Fractions
Question 1.
Alice is filling candy molds with chocolate for her brother’s birthday party. It takes her 6 minutes to fill 5 of the molds. How long will it take her to fill all of the molds? Complete the ratio table to show the answer.
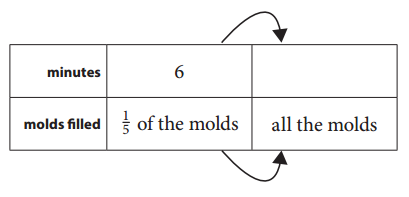
Answer:
Given that Alice is filling candy molds with chocolate for her brother’s birthday party. It takes her 6 minutes to fill 5 of the molds.
\(\frac{1}{5}\) of the molds take 6 minutes.
\(\frac{1}{5}\)×5 = 6×5 = 30
It will take 30 minutes to fill all the molds.
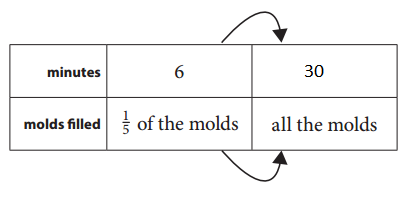
Question 2.
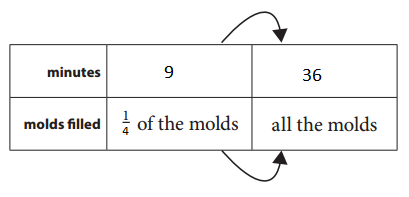
Alice is filling cupcake molds with old, melted crayons to make new crayons for her brother’s party. If it takes her 9 minutes fill \(\frac{1}{4}\) of the molds, how long will it take her to fill all the molds? Show your thinking on a ratio table.
Answer:
Given that Alice is filling cupcake molds with old, melted crayons to make new crayons for her brother’s party.
It will take 9 minutes to fill \(\frac{1}{4}\) of the molds,
\(\frac{1}{4}\) × 4 = 9×4 = 36
It will take 36 minutes to fill all molds.
Question 3.
Write a story problem for the expression 14 ÷ \(\frac{1}{2}\). Then solve the problem. NOTE Remember that 14 ÷ \(\frac{1}{2}\) means, “How many halves are there in 14?”
Answer:
14 ÷ \(\frac{1}{2}\) means 28.
Story problem: There are 28 members in the party and Alice wants to divide the cake in equal halves for all 28 members.