Students looking for the Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 7 Module 1 can find a better approach to solve the problems.
Bridges in Mathematics Grade 5 Home Connections Answer Key Unit 7 Module 1
Bridges in Mathematics Grade 5 Home Connections Unit 7 Module 1 Session 1 Answer Key
More Array Work
Fill in the blanks on each array. Then write two equations—one multiplication and one division—to match the array.
Question 1.
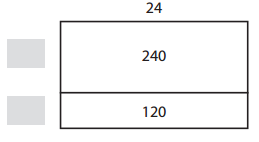
_____________ × ______________ = ______________
_____________ ÷ ______________ = ______________
Answer:
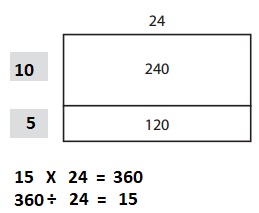
Explanation:
Given from above the two equations which match the array one multiplication and one division are 24 X 15 = 360 ; 360 ÷ 15 = 24 .
Question 2.
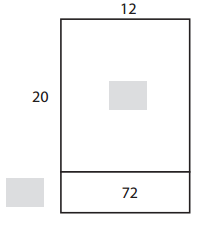
_____________ × ______________ = ______________
_____________ ÷ ______________ = ______________
Answer:
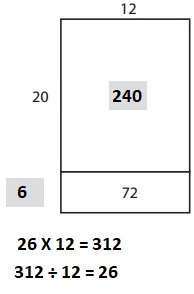
Explanation:
Given from above the two equations which match the array one multiplication and one division are 26 X 12 = 312 ; 312 ÷ 26 = 12.
Question 3.
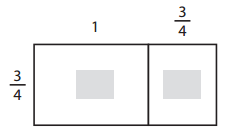
_____________ × ______________ = ______________
_____________ ÷ ______________ = ______________
Answer:
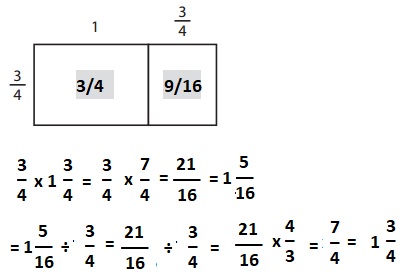
Explanation:
Given from above the two equations which match the array one multiplication and one division is 1 3/4 X 3/4 = 1 5/16 ; 1 5/16 ÷ 1 3/4 = 3/4.
Question 4.

_____________ × ______________ = ______________
_____________ ÷ ______________ = ______________
Answer:
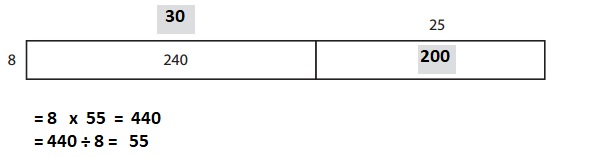
Explanation:
Given from above the two equations which match array one is multiplication and one is division is 55 X 8 = 440 ; 440 ÷ 55 = 8 .
Question 5.
Evaluate each expression.
a. (12 × 4) × \(\frac{1}{4}\) = _______________
Answer:
(12 X 4) X \(\frac{1}{4}\) = 12,
Explanation:
Given from above question first multiply brackets that is (12 X 4) = 48 and then multiply to fraction so, 48 X (1/4) = 48/4 =12.
b. 48 × (6 × \(\frac{1}{3}\)) = _______________
Answer:
48 X ( 6 X \(\frac{1}{3}\))= 96,
Explanation:
Given from above expression first multiply the brackets that is ( 6 X (1/3)) = 6/3 = 2 so therefore multiply to 48 that is 48 X 2 = 96.
c. \(\frac{3}{5}\) × (4 × 5) = _______________
Answer:
\(\frac{3}{5}\) X ( 4 X 5 ) = 12,
Explanation:
Given from above expression first multiply brackets that is ( 4 X 5 ) = 20 and then multiply to fraction that is (3/5) X 20 = 3 X 4 = 12.
d. 16 × (\(\frac{3}{4}\) × 1) = _______________
Answer:
16 X (\(\frac{3}{4}\) X 1 ) = 12,
Explanation:
Given from above expression first multiply (3/4) X 1 = 3/4 and then multiply to 16 that is 16 X (3/4) = 4 X 3 =12.
e. \(\frac{1}{2}\) × (6 × \(\frac{2}{3}\)) = ________________
Answer:
\(\frac{1}{2}\) X ( 6 X \(\frac{2}{3}\)) = 2,
Explanation:
Given from above expression first evaluate ( 6 X (2/3)) = 2 X 2 = 4 and then now multiply to fraction that is (1/2) X 4 = 4/2 = 2.
Question 6.
Ben drove \(\frac{4}{7}\) of the way to his friend’s house before he stopped to eat lunch. If the distance to his friend’s house was a total of 427 miles, how far did Ben drive before he stopped for lunch? Show your work.
Answer:
244 miles did Ben drive before he stopped for lunch,
Explanation:
Given from above fraction of the way Ben drove to his friend’s house is 4/7 and total distance to his friend’s house was 427 miles so therefore ,

Question 7.
Sage hiked 12\(\frac{1}{2}\) miles one day on her vacation. Her younger brother Chase hiked \(\frac{1}{4}\) as far as Sage. How far did Chase hike? Show your work.
Answer:
3 \(\frac{1}{8}\) miles did Chase hike ,
Explanation:
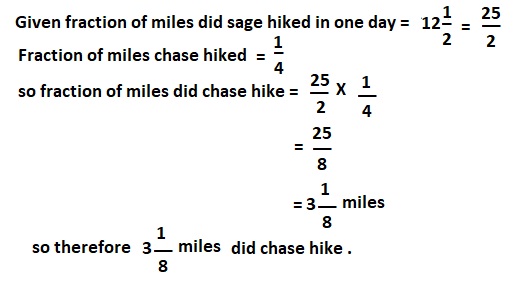
Question 8.
CHALLENGE Randy drank \(\frac{3}{4}\) of a 250 ml container of juice for breakfast, 3\(\frac{5}{6}\) 150 ml water bottles throughout the day, and \(\frac{7}{8}\) of a 400 ml smoothie for dinner.
a. Write an expression to show how much liquid Randy drank in all.
Answer:
(\(\frac{3}{4}\) X 250 ml) + ( (3 \(\frac{5}{6})\) X 150 ml) + (\(\frac{7}{8}\)) X 400 ml,
Explanation:
Given from above the expression which Randy drank in all as a juice for breakfast , water bottles through out the day and smoothie for dinner.
b. How many milliliters did Randy drink in all? Show your work.
Answer:
1,112 \(\frac{1}{2}\) ml did Randy drink in all,
Explanation:
Given from above No of ml of juice did Randy drank for breakfast is 3/4 of 250ml ;No of ml of water bottles did Randy drank through out day is 3(5/6) of 150ml and No of ml of smoothie for dinner is (7/8) of 400ml so therefore,

so, therefore Randy drank 1,112 1/2 ml in all.
c. How many liters is this?
Answer:
1.1125 liters,
Explanation:
As we know that 1 liter is equals to 1000 ml so, 1 ml is equals to 0.001 liter so, therefore 1,112.5 X 0.001 = 1.1125 liters.
Bridges in Mathematics Grade 5 Home Connections Unit 7 Module 1 Session 4 Answer Key
More Roll Five & Ratio Tables
Victor and Juan were playing Roll Five. They have to add, subtract, multiply or divide any of the digits on their five dice to reach their target number. Players are awarded 1 point for each digit used.
Question 1.
Victor’s target number is 18. He rolled the digits 2, 2, 6, 7, and 9.
a. Victor knows he can record 2 × 9 to make 18, but he wants to find another expression that will give him a higher score. Record an expression Victor could use.
Answer:
2 + 7 + 9 = 18 ; ( 7 – 6 ) X 2 X 9 = 18 ,
Explanation:
Given from above the another expression which Victor could use by using 3 digits is 2 + 7 + 9 = 18 ; and by using 4 digits is ( 7 – 6 ) X 2 X 9 = 18.
b. What is Victor’s score?
Answer:
2 , 3 , 4 , or 5 .
Explanation:
Given from above the Victor’s score will be 2 ,3 4 or 5 as depending on the expression chosen by Victor .
c. Victor thinks he can start with 7, subtract 2, subtract another 2, and then multiply by 6 to get 18. Juan says that the expression Victor recorded, 7 – 2 – (2 × 6), does not reach 18. How can Victor rewrite his expression so that he gets a total of 18?
Answer:
( 7 – 2 – 2 ) X 6 = 18 ,
Explanation:
Given from above expression victor recorded 7 – 2 – ( 2 X 6 ) but does not reach to 18 so ,if we write as expression ( 7 – 2 – 2 ) X 6 = 3 X 6 =18 .
d. What is Victor’s score?
Answer:
4,
Explanation:
Given from above the higher digit is 4 so, the victor awarded as 4 points respectively.
Question 2.
Juan’s target number is 36. He rolled the digits 2, 4, 2, 5, and 8.
a. Juan says that 4 less than 8 times 5 is 36. Write an expression to record his thinking, and then solve the problem to see if Juan gets his target number.
Answer:
( 8 X 5 ) – 4 = 36 ,
Expression:
Given from above Juan’s target number is 36 so , 8 times 5 is written as ( 8 X 5) and 4 is less than means subtract 4 from (8 X 5) that is the expression is ( 8 X 5) – 4 = 40 – 4 = 36 .
b. Record another equation Juan could use to reach his target number.
Answer:
(4 + 2) X (8 – 2)= 36,
Expression:
Given from above the another equation is that (4 + 2) X ( 8 – 2) = 6 X 6 = 36 .
Question 3.
Later, Victor was solving the problem 483 ÷ 21. He started the ratio table below. Complete the ratio table to find the quotient. Add to Victor’s ratio table as needed.

483 ÷ 21 = __________________
Answer:
483 ÷ 21 = 23 ,
Explanation:

given from question completed the ratio table and found the quotient that is 483 ÷ 21 = 23 .
Question 4.
Victor also needed to solve 870 ÷ 30. Help him by filling in the ratio table below to solve 870 ÷ 30.

870 ÷ 30 = __________________
Answer:
870 ÷ 30 = 29 ,
Explanation:

Given from above completed the ratio table and find the quotient that is 870 ÷ 30 = 29.
Question 5.
Find the quotient of 608 ÷ 32. Model your thinking with a rectangular array or an area model.
Answer:
608 ÷ 32 = 19,
Explanation:

Given from the question 608 ÷ 32 by using rectangular array area model we get quotient as 19 so, first divide into two boxes and then multiply the number that is 32 X 1 =32 that is 608 – 32 = 288 now again multiply 32 X 9 = 288 then remainder is 0 so , the quotient is 10 + 9 = 19 therefore 608 ÷ 32 = 19.
Question 6.
Fill in chart below to round each number to the nearest one, tenth, and hundredth.
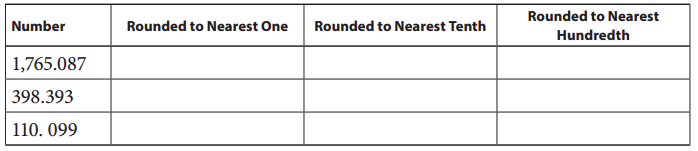
Answer:
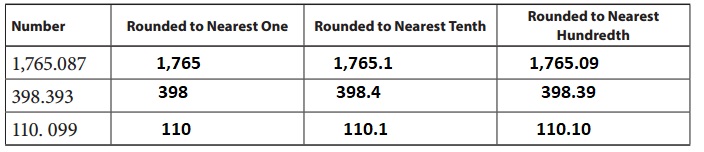
Explanation:
Given from above completed the table by rounding to nearest one , tenth and hundredth.
Question 7.
CHALLENGE Annie needed to solve 855 ÷ 19. She thought she would solve 855 ÷ 20 and then adjust, since 20 is an easier number to work with than 19. Can she solve the problem this way? Why or why not? Explain your thinking.
Answer:
Yes she can solve,
Explanation:
Given that Annie thought that 20 is an easier number to work with than 19 therefore she can solve as dividing by 20 gives 1 less every time ,so you can just add to the result you get when you divide 855 from 20.
Bridges in Mathematics Grade 5 Home Connections Unit 7 Module 1 Session 6 Answer Key
More Division with Fractions
Question 1.
Jamal can paint \(\frac{1}{5}\) of his closet in 12 minutes. How long will it take him to paint the entire closet? Complete the ratio table to show the answer.
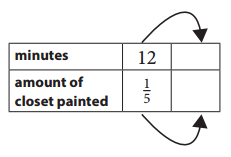
Answer:
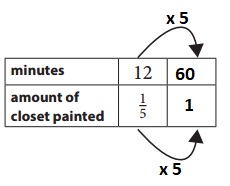
Explanation:
Given from above ratio table so, 12 X 5 = 60 minutes and amount of closet painted is 1/5 x 5 = 1 .
Question 2.
Frank can clean \(\frac{1}{4}\) of his room in 15 minutes. How long will it take Frank to clean the entire room? Show your thinking on a ratio table.
Answer:
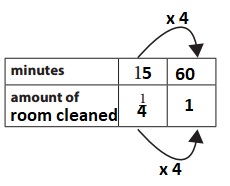
It will take 60 minutes to clean the entire room, Full room is cleaned,
Explanation:
Given from above ratio table number of minutes Frank can clean is 15 minutes so, 15 X 4 = 60 minutes so, amount of room cleaned (1/4) X 4 = 1.
Question 3.
Write a story problem for the expression 15 ÷ \(\frac{1}{3}\). Then solve the problem.
NOTE Remember that 15 ÷ \(\frac{1}{3}\) means, “How many thirds are there in 15?”
Answer:
Story problem:
Harry can make 1 bracelet using \(\frac{1}{3}\) of beads of box, If there are 15 boxes of beads how many number of bracelets can Harry make?
Harry can make 45 bracelets,
Explanation:
Asked to write a story problem for the expression 15 ÷ \(\frac{1}{3}\). Then to solve the problem. So story problem is Harry can make 1 bracelet using \(\frac{1}{3}\) of beads of box, If there are 15 boxes of beads how many number of bracelets can Harry make? Solving we get 15 ÷ \(\frac{1}{3}\) = 15 X 3 = 45 bracelets.
Review
Question 4.
Find the sum or difference.
a. \(\frac{2}{3}\) + \(\frac{4}{9}\)
Answer:
\(\frac{2}{3}\) + \(\frac{4}{9}\) = 1\(\frac{1}{9}\),
Explanation:
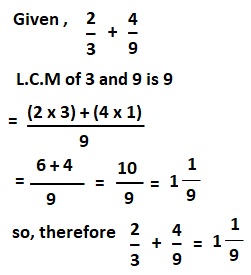
b. \(\frac{3}{5}\) + \(\frac{5}{12}\)
Answer:
\(\frac{3}{5}\) + \(\frac{5}{12}\) = 1 \(\frac{1}{60}\),
Explanation:
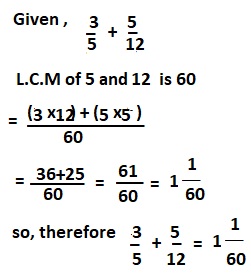
c. 1\(\frac{1}{3}\) + \(\frac{7}{9}\)
Answer:
1\(\frac{1}{3}\) + \(\frac{7}{9}\) = 2\(\frac{1}{9}\),
Explanation:
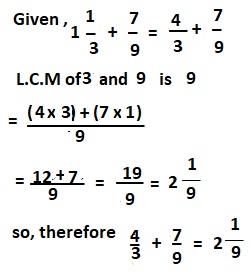
d. 2\(\frac{4}{5}\) – \(\frac{11}{12}\)
Answer:
2\(\frac{4}{5}\) – \(\frac{11}{12}\) = 1\(\frac{53}{60}\),
Explanation:
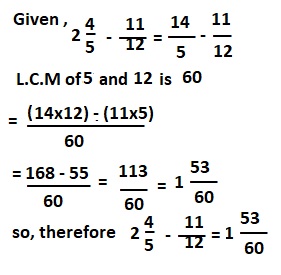
e. \(\frac{6}{7}\) – \(\frac{1}{2}\)
Answer:
\(\frac{6}{7}\) – \(\frac{1}{2}\) = \(\frac{5}{14}\),
Explanation:
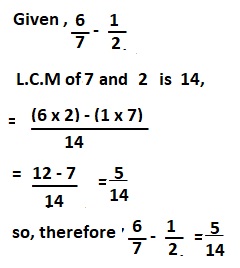
f. 2\(\frac{1}{9}\) – \(\frac{5}{6}\)
Answer:
2\(\frac{1}{9}\) – \(\frac{5}{6}\) = 1 \(\frac{5}{18}\),
Explanation:
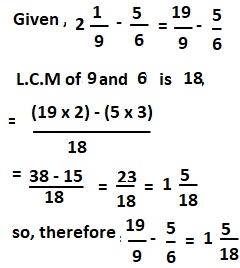
Question 5.
Ling is solving the problem 125 × 16.
a. Use the standard algorithm to find the product of 125 × 16.
Answer:
125 X 16 = 2,000,
Explanation:

so therefore solved 125 X 16 by using standard algorithm and the answer is 2,000.
b. Use another strategy to solve 125 × 16. Think of the most efficient strategy you know.
Answer:
125 X 16 =2,000,
Explanation:
125 X 16 = ( 100 + 25 ) X 16 = (100 X 16 ) + ( 25 X 16 ) = 1600 + 400 = 2,000 this is the most efficient strategy which the number split into two and multiply to given number and add them then we get 125 X 16 = 2000.
Question 6.
Convert the following measurements.
a. 1.2 liters = _______________ ml
Answer:
1.2 liters = 1,200ml,
Explanation:
As we know 1 liter = 1000 ml so, therefore 1.2 liters = 1.2 X 1000 = (12/10) X 1000 ml =1,200 ml .
b. 13,000 ml = ______________ liters
Answer:
13,000 ml = 13 liters ,
Explanation:
As we know that 1ml =0.001 liter so, given 13,000ml = 13,000 X 0.0001= 13,000 X (1/1,000) = 13 liters respectively.
c. 26.74 liters = _______________ ml
Answer:
26.74 liters = 26,740 ml ,
Explanation:
As we know that 1 liter = 1,000 ml so, given 26.74 liters = 26.74 X 1,000 = (2,674/100) X 1,000 =26,740 ml respectively.
d. 2,675 ml = _______________ liters
Answer:
2,675 ml = 2.675 liters,
Explanation:
As we know that 1 ml = 0.001 liters so ,given 2,675 ml = 2,675 X 0.001 = 2,675 X (1/1000) = 2,675/1000 = 2.675 liters respectively.
e. CHALLENGE 3 days = ______________ seconds
Answer:
3 days = 2,59,200 seconds ,
Explanation:

so, therefore 3 days = 2,59,200 seconds.