Bridges in Mathematics Grade 4 Student Book Unit 3 Module 1 Answer Key

Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 3 Module 1 will help students analyze their level of preparation.

Bridges in Mathematics Grade 4 Student Book Answer Key Unit 3 Module 1

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 1 Session 1 Answer Key

Skills Practice

Question 1.
Fill in the blanks.
a. ml = ____ 6 liters
Answer: 6000 ml
1 liter = 1000 ml
6 liters = ?
6 liters = 6 x 1000 = 6000 ml

b. 10 liters = ____ ml
Answer: 10000 ml
1 liter = 1000
10 liters = ?
10 liters = 10 x 1000 = 10000

Question 2.
Fill in the blanks on the ratio table.

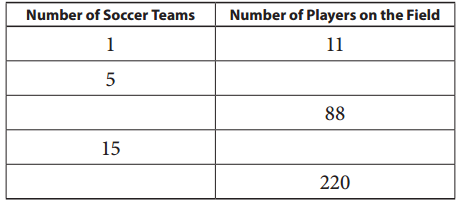
Answer:

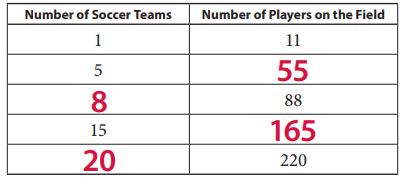
A team of soccer has 11 players on the field.
The number of players on the field for 5 number of soccer teams is 55
The number of players on the field for 15 number of soccer teams is 165
The number of players on the field is 88 for 8 number of soccer teams
The number of players on the field is 220 for 20 number of soccer teams

Question 3.
Which of the following lists contains only prime numbers?
13, 18, 21
15, 19, 27
11, 17, 31
7, 23, 39
Answer: 11, 17, 31
Prime number: The number which is divided by 1 and the number itself. In the above options the numbers are 11, 17, 31

Question 4.
Multiply.

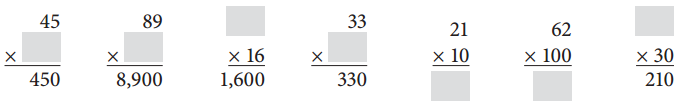
Answer:

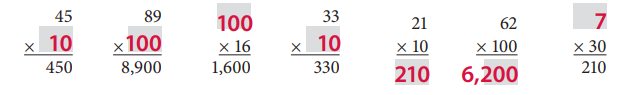
Multiplication was performed for the above given problems.
If two numbers are given, we need to multiply both the numbers to get the result.
When a number and the result, which is the product of two numbers are given, then divide the resulted product with the give number to get another number.

Question 5.
There are 48 kids and 6 adults in the After-School Club, and they’re all going to the zoo this afternoon. Each van holds 7 people. How many vans will the After-School Club need for this trip?

Use numbers, labeled sketches, or words to solve this problem.
Write the answer on the line below.

The After-School Club will need ____ vans to take all 54 people to the zoo.
Answer: The number of vans that are needed for this trip is 8.
Total number of kids = 48 kids
number of adults = 6
each van holds 7 people.
number of vans required = (48 + 6 ) / 7 = 54 / 7 = 7.71 = 8 (approximately)

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 1 Session 2 Answer Key

Fair Shares

Work with a partner to solve at least two of the three problems on this page and the next. Use numbers, words, and labeled sketches to show all of your thinking. If you solve all three and have extra time, start the challenge problem on the next page.

Question 1.
Sally and her friends Vanessa, Ellie, and Helen have 3 strips of dried fruit to share. Each strip is 1″ wide and 12″ long. If the 4 girls share the strips fairly, how much will they each get?

Answer: $\frac{3}{4}$
Number of strip of dried fruit = 3
Number of girls = 4
Therefore, each will get $\frac{3}{4}$.

Question 2.
One Saturday morning, Eduardo and his sister invited their two friends over to play. Before long, things were getting pretty noisy around the house, and Mrs. Ortega said, “If the four of you will pick up all the toys downstairs, I’ll give you $3.00 to spend at the corner store.” If the 4 kids share the $3.00 fairly, how much money will they each get?

Answer: $\frac{3}{4}$
Number of persons = 4
each person will get $3.00
Therefore, 4 kids share the $3.00 fairly, then each will get $\frac{3}{4}$

Question 3.
The gym at our school is open every evening from 5:00 to 8:00. If 4 different
basketball teams want to use the gym on Thursday evening and they agree to split the time equally, how much practice time will each team get?
Answer: $\frac{3}{4}$
Number of hours = 2
Number of different basketball teams = 4
therefore, each team wil get $\frac{3}{4}$ hours.

Question 4.
CHALLENGE The coach took us out for pizza after our last game. There were 14 of us, so we had to split up and sit at different tables. Six of us sat at one table and got 4 medium pizzas to share equally. The other 8 of us sat at a different table and got 6 medium pizzas to share equally. Afterwards, Keira said it wasn’t fair because some kids got more pizza than others. Do you agree with her? Use numbers, words, or labeled sketches to explain your answer.

Answer: Yes I will agree with Keira
number of pieces of medium pizza = 6
first group:
Number of pizzas = 4
Number of total pizza pieces = 6 x 4 = 24
Number of people = 6
Therefore, each person will get = 24 / 6 = 4
second group:
Number of pizzas = 6
Number of total pizza pieces = 6 x 6 = 36
Number of people = 8
Therefore, each person will get = 36 / 8 = 4.5
therefore, keira is correct.

Share & Share Alike

Question 1.
Solve each problem below. Show your work using numbers, labeled sketches, or words.

a. Carmen has four cookies. Her friend Elisa joins her. Carmen shares her cookies evenly with her friend. How many cookies does each girl each get?
Answer: 2 cookies each one get
Number of cookies Carmen has = 4
Carmen shares her cookies evenly with her friend.
therefore, number of people for sharing = 2
cookies does each girl each get = 4 / 2 = 2

b. Carmen and Elisa are about to eat the cookies when Sam and Michael join them. Carmen and Elisa share the cookies evenly with Sam and Michael. How many cookies does each person get?
Answer: 1 cookie each
Number of cookies Carmen has = 4
therefore, number of people for sharing = 4
cookies does each girl each get = 4 / 4 = 1

c. The group is about to eat their cookies when four more friends join them. Carmen collects the cookies and divides them evenly between all eight people. How many cookies does each person get?
Answer: $\frac{1}{2}$ cookies get each
Number of cookies Carmen has = 4
therefore, number of people for sharing = 8
cookies does each girl each get = 4 / 8 = $\frac{1}{2}$

d. The cookies are eaten by the eight people. Imagine, though, that eight more people joined the group before they ate the cookies, and they all shared the cookies evenly. How much would each person have been given?
Answer: $\frac{1}{4}$ cookies each get
Number of cookies Carmen has = 4
therefore, number of people for sharing = 16
cookies does each girl each get = 4 / 16 = $\frac{1}{4}$

Question 2.
Fill in the blank for each equation below.
a 20 × 35 = 2 × _____
Answer: 350
20 x 35 = 700
2 x 350 = 700

b. 10 × ____ = 10 × 5 × 3
Answer: 15
10 x 5 x 3 = 150
10 x 15 = 150

c. ___ × 30 = 9 × 100
Answer: 30
9 x 100 = 900
30 x 30 = 900

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 1 Session 3 Answer Key

Fractions & Mixed Numbers

Question 1.
Change each of the fractions below into a mixed number. Use a labeled sketch and

a.

Answer:

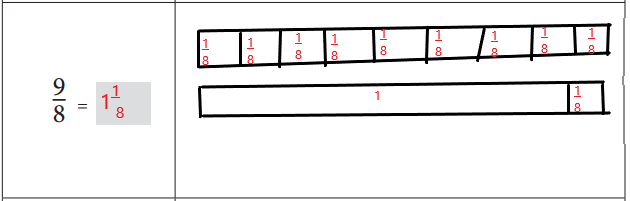
$\frac{9}{8}$ in mixed fraction can be written as 1$\frac{1}{8}$

b.

Answer:

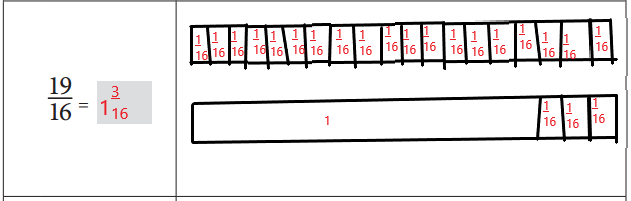
$\frac{19}{16}$ in mixed fraction can be written as 1$\frac{3}{16}$

c.

Answer:

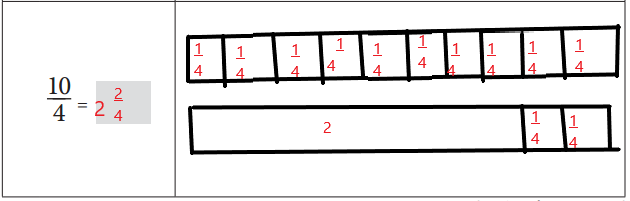
$\frac{10}{4}$ in mixed fraction can be written as 2$\frac{2}{4}$

Question 2.
For each of the problems on this page:

Solve the problem and show your thinking with numbers, words, or labeled sketches. Use your fraction pieces to help if you want.
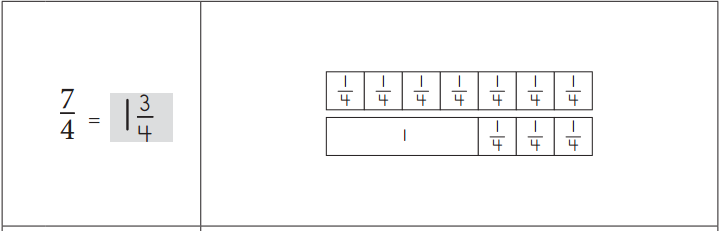
If the answer turns out to be an improper fraction (like $\frac{3}{2}$ or $\frac{7}{4}$) rename it as a mixed number (like 1$\frac{1}{2}$ or 1$\frac{3}{4}$).

a. Carlos and his mom went out on a bike ride. They rode $\frac{5}{8}$ of a mile to the park, and then $\frac{5}{8}$ of a mile back home. How far did they ride in all?

Answer: $\frac{10}{8}$
rode $\frac{5}{8}$ of a mile to the park
$\frac{5}{8}$ of a mile back home
Total distance he travelled = distance travelled to park + distance travelled to home
= $\frac{5}{8}$ + $\frac{5}{8}$ = $\frac{10}{8}$

b. It takes $\frac{3}{4}$ of a cup of orange juice to make 1 smoothie. Erin wants to make 2 smoothies. How much orange juice will she need?

Answer: $\frac{6}{4}$
Number of smoothies Erin wants = 2
Orange juice required for one smoothie = $\frac{3}{4}$
Therefore, orange juice required for two smoothies = $\frac{3}{4}$ + $\frac{3}{4}$ = $\frac{6}{4}$

Question 3.
Change each of the mixed numbers below into a fraction. Use your fraction pieces to help.
ex
1$\frac{3}{4}$ = $\frac{7}{4}$

a. 1$\frac{3}{8}$ =
Answer: $\frac{11}{8}$
1$\frac{3}{8}$ = $\frac{11}{8}$

b. 1$\frac{5}{16}$ =
Answer: $\frac{21}{16}$
1 $\frac{5}{16}$ = $\frac{21}{16}$

c. 2$\frac{1}{2}$ =
Answer: $\frac{5}{2}$
2 $\frac{1}{2}$ = $\frac{5}{2}$

d. 2$\frac{2}{4}$ =
Answer: $\frac{10}{4}$
2 $\frac{2}{4}$ = $\frac{10}{4}$

e.
1$\frac{7}{8}$ =
Answer: $\frac{15}{8}$
1 $\frac{7}{8}$ = $\frac{15}{8}$

Fractions & Mixed Numbers on a Number Line

Question 1.
Use the number line to answer the questions below.

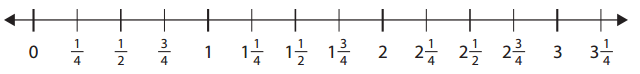
ex
What improper fraction is equal to 2$\frac{1}{4}$ ? In other words, how many fourths are in two and one-fourth?
$\frac{9}{4}$

ex
What number is halfway between 2 and 3?
2$\frac{1}{2}$

a. What improper fraction is equal to 1$\frac{1}{2}$ ? In other words, how many halves are in one and one-half?
Answer; $\frac{3}{2}$
1$\frac{1}{2}$ = $\frac{3}{2}$
The improper fraction is equal to 1$\frac{1}{2}$ is $\frac{3}{2}$

b. What mixed number is equal to $\frac{6}{4}$ ?
Answer: 1$\frac{2}{4}$ or 1$\frac{1}{2}$
The mixed number is equal to $\frac{6}{4}$ is 1$\frac{2}{4}$ or 1$\frac{1}{2}$ .

c. Which is greater, $\frac{5}{4}$ or 1$\frac{1}{2}$ ?
Answer: 1$\frac{1}{2}$
1$\frac{1}{2}$ = $\frac{3}{2}$ = 1.5
$\frac{5}{4}$ = 1.25
As 1.5 is greater than 1.25. Hence, 1$\frac{1}{2}$ is greater than $\frac{5}{4}$

d. What mixed number is equal to $\frac{13}{4}$ ?
Answer: 3$\frac{1}{4}$
The mixed number is equal to $\frac{13}{4}$ is 3$\frac{1}{4}$

e. What improper fraction is equal to 2$\frac{1}{2}$ ? In other words, how many halves are in two and one-half?
Answer: $\frac{5}{2}$
The improper fraction is equal to 2$\frac{1}{2}$ is $\frac{5}{2}$

f. Which is greater, 1$\frac{3}{4}$ or $\frac{8}{4}$ ?
Answer: $\frac{8}{4}$
1$\frac{3}{4}$ = $\frac{7}{4}$
$\frac{8}{4}$ is greater than $\frac{7}{4}$

Challenge

Question 2.
What number is halfway between 0 and 1?
Answer: $\frac{1}{2}$
The number is halfway between 0 and 1 is $\frac{1}{2}$

Question 3.
What number is halfway between 0 and 3?
Answer: 1$\frac{1}{2}$
The number is halfway between 0 and 3 is 1$\frac{1}{2}$ .

Question 4.
What number is halfway between 0 and 17?
Answer: 8$\frac{1}{2}$
The number is halfway between 0 and 17 is 8$\frac{1}{2}$

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 1 Session 4 Answer Key

Fractions & Division Tables

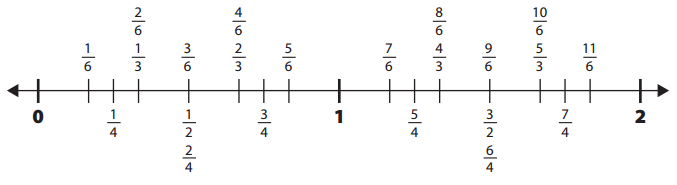
Question 1.
Write a greater than (>), less than (<), or equal sign in the circle to complete each equation below. Use the number line to help figure out which fraction is greater.
ex
$\frac{1}{4}$ $\frac{1}{2}$

a.
$\frac{3}{4}$ $\frac{5}{6}$
Answer: $\frac{3}{4}$ < $\frac{5}{6}$
$\frac{3}{4}$ = 0.75
$\frac{5}{6}$ = 0.833
Therefore, $\frac{3}{4}$ < $\frac{5}{6}$

b.
$\frac{2}{3}$ $\frac{4}{6}$
Answer: $\frac{2}{3}$ = $\frac{4}{6}$
$\frac{2}{3}$ = 0.667
$\frac{4}{6}$ = 0.667
Therefore, $\frac{2}{3}$ = $\frac{4}{6}$

c.
$\frac{5}{3}$ $\frac{5}{4}$
Answer: $\frac{5}{3}$ > $\frac{5}{4}$
$\frac{5}{3}$ = 1.667
$\frac{5}{4}$ = 1.25
Therefore, $\frac{5}{3}$ > $\frac{5}{4}$

d.
$\frac{2}{3}$ $\frac{3}{2}$
Answer: $\frac{2}{3}$ < $\frac{3}{2}$
$\frac{2}{3}$ = 0.667
$\frac{3}{2}$ = 1.5
Therefore, $\frac{2}{3}$ < $\frac{3}{2}$

e.
$\frac{1}{3}$ $\frac{3}{6}$
Answer: $\frac{1}{3}$ < $\frac{3}{6}$
$\frac{1}{3}$ = 0.334
$\frac{3}{6}$ = 0.5
Therefore, $\frac{1}{3}$ < $\frac{3}{6}$

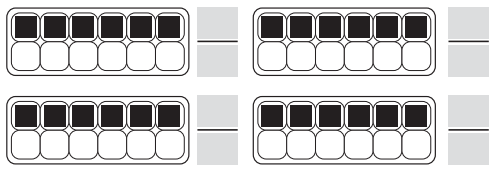
Question 2.
Complete the division tables below.

a.

Answer:

The above division table can be formed by dividing 70, 90,20,80,30, 50, 60, 40 with 10, which results in 7, 9, 2, 8, 3, 5, 6, 4

b.

Answer:

The above division table can be formed by dividing 15, 30, 35, 25, 10, 45, 20, 40 with 5, which results in 3, 6, 7, 5, 2, 9, 4, 8

c.

Answer:

The above division table can be formed by dividing 8, 20, 16, 36, 24, 28, 12, 32 with 4, which results in 2, 5, 4, 9, 6, 7, 3, 8

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 1 Session 5 Answer Key

Dividing an Egg Carton

Use yarn or string to divide your carton into 2 equal parts.

Use yarn or string to divide your carton into 3 equal parts.

Use yarn or string to divide your carton into 4 equal parts.

Use yarn or string to divide your carton into 6 equal parts.

Use yarn or string to divide your carton into 12 equal parts.

Egg Carton Recording Paper

Answer:

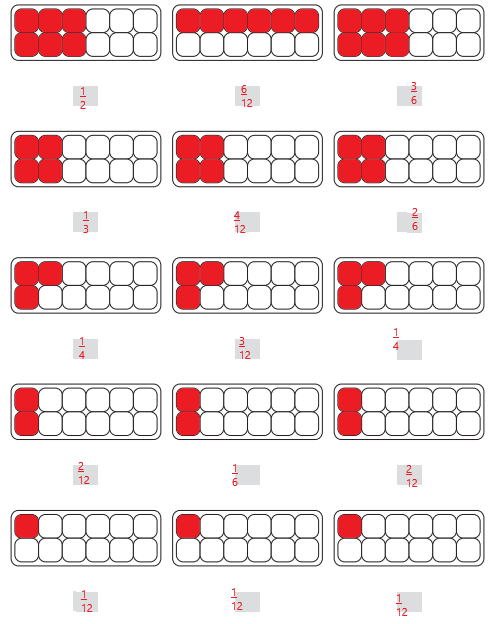
By using yarn or string to divide your carton into 2 equal parts, the fractions are $\frac{1}{2}$, $\frac{6}{12}$, $\frac{3}{6}$ and the same was represented in red in the above figure.
By using yarn or string to divide your carton into 3 equal parts, the fractions are $\frac{1}{3}$, $\frac{4}{12}$, $\frac{2}{6}$ and the same was represented in red in the above figure.
By using yarn or string to divide your carton into 4 equal parts, the fractions are $\frac{1}{4}$, $\frac{3}{12}$, $\frac{1}{4}$ and the same was represented in red in the above figure.
By using yarn or string to divide your carton into 6 equal parts, the fractions are $\frac{2}{12}$, $\frac{1}{6}$, $\frac{2}{12}$ and the same was represented in red in the above figure.
By using yarn or string to divide your carton into 12 equal parts, the fractions are $\frac{1}{12}$, $\frac{1}{12}$, $\frac{1}{12}$ and the same was represented in red in the above figure.

Comparing Fractions

Challenge

1. In the boxes below, list the fractions you just modeled in order from least to greatest.

Answer:

$\frac{1}{12}$ < $\frac{1}{6}$ < $\frac{1}{4}$ < $\frac{1}{3}$ < $\frac{1}{2}$ < $\frac{3}{4}$ < $\frac{5}{6}$ < 1
2. Find a partner to work with. For each pair of fractions below, talk about which is larger and why. You can use the egg cartons to model and compare the fractions, but try to see if you can picture them in your head and reason about which must be larger.

a.

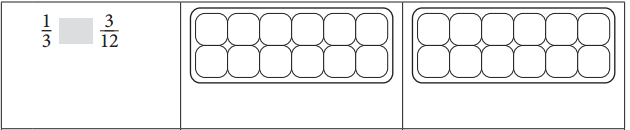
Answer:

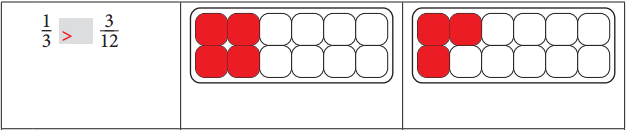
$\frac{1}{3}$ > $\frac{3}{12}$. The same equation was illustrated in the adjacent figure in red color.

b.

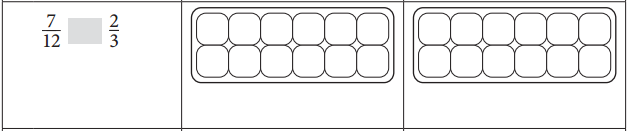
Answer:

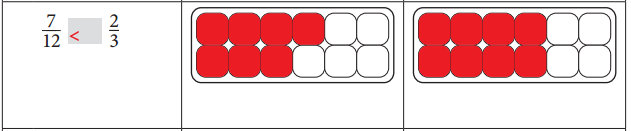
$\frac{7}{12}$ < $\frac{2}{3}$. The same equation was illustrated in the adjacent figure in red color.

c.

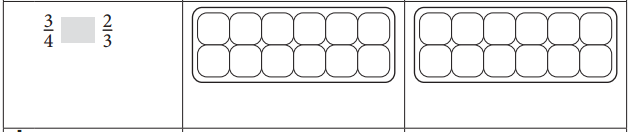
Answer:

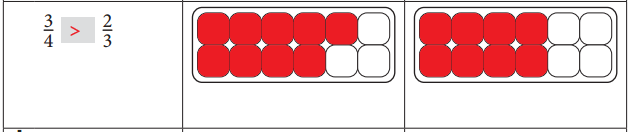
$\frac{3}{4}$ > $\frac{2}{3}$. The same equation was illustrated in the adjacent figure in red color.

d.

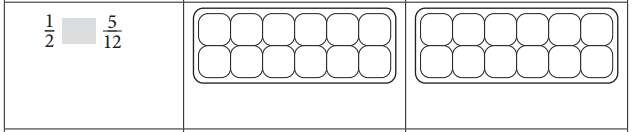
Answer:

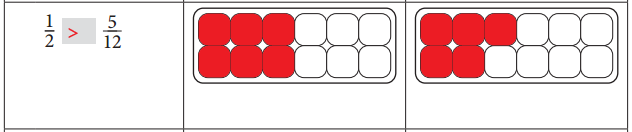
$\frac{1}{2}$ > $\frac{5}{12}$. The same equation was illustrated in the adjacent figure in red color.

e.

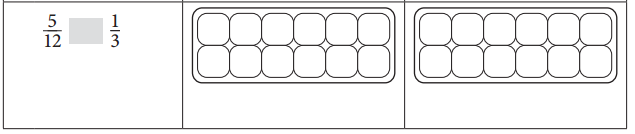
Answer:

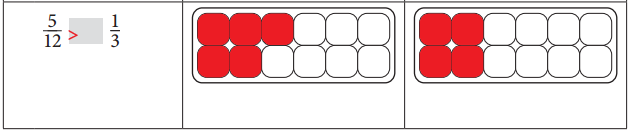
$\frac{5}{12}$ > $\frac{1}{3}$. The same equation was illustrated in the adjacent figure in red color.

Modeling Egg Carton Fractions

Question 1.
Use your egg carton diagram, string, and tiles to build a model of each fraction. Then draw a sketch of each fraction in the tables.

Answer:

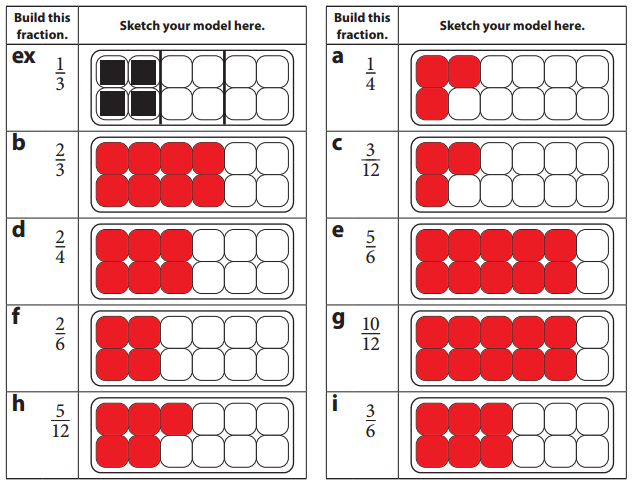
The given fractions are all indicated in red color in the above figure.

Question 2.
What observations can you make about $\frac{3}{6}$ and $\frac{2}{4}$ ?
Answer: $\frac{3}{6}$ = $\frac{1}{2}$ = 0.5
$\frac{2}{4}$ = $\frac{1}{2}$ = 0.5
In $\frac{3}{6}$ we are taking 3 parts from total 6 parts. But where as in $\frac{2}{4}$ we are using 2 parts from total 4 parts.
So we are using half of the amount in total amount.

Question 3.
Which is more, $\frac{1}{4}$ of a dozen or $\frac{1}{3}$ of a dozen? _____

a. How do you know?
Answer: $\frac{1}{3}$ is more
$\frac{1}{4}$ = 0.25
$\frac{1}{3}$ = 0.334
As 0.334 is more than 0.25. Hence $\frac{1}{3}$ is more than $\frac{1}{4}$

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 1 Session 6 Answer Key

Equivalent Fractions

In each problem below, there are 2, 3, or even 4 identical pictures. Label each with a different fraction name, and draw in yarn lines to show your thinking. In all problems, one egg carton is always worth 1.

Question 1.

Answer:

The shaded region can be represented in $\frac{2}{12}$ , $\frac{1}{6}$.

Question 2.

Answer:

The shaded region can be represented in $\frac{4}{6}$ , $\frac{2}{3}$ , $\frac{8}{12}$.

Question 3.

Answer:

The shaded region can be represented in $\frac{3}{12}$ , $\frac{1}{4}$

Question 4.

Answer:

The shaded region can be represented in $\frac{3}{4}$ , $\frac{9}{12}$

Question 5.

Answer:

The shaded region can be represented in $\frac{4}{12}$ , $\frac{2}{6}$ , $\frac{1}{3}$.

Question 6.

Answer:

The shaded region can be represented in $\frac{10}{12}$ , $\frac{5}{6}$

Question 7.

Answer:

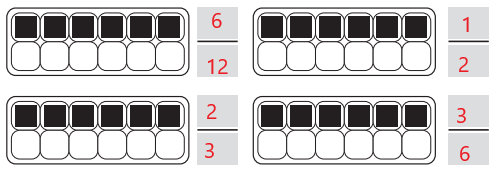
The shaded region can be represented in $\frac{6}{12}$ , $\frac{1}{2}$, $\frac{2}{3}$ , $\frac{3}{6}$

Question 8.

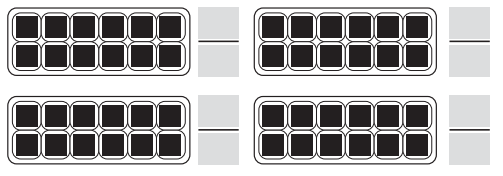
Answer:

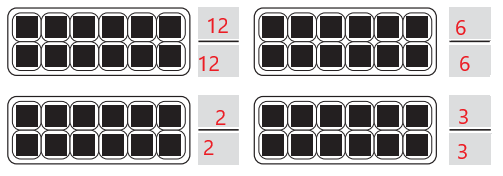
The shaded region can be represented in $\frac{12}{12}$ , $\frac{2}{2}$, $\frac{3}{3}$ , $\frac{6}{6}$

Question 9.
Can you come up with 4 different ways to name a carton and a half of eggs? (Hint: Use mixed numbers or improper fractions.)

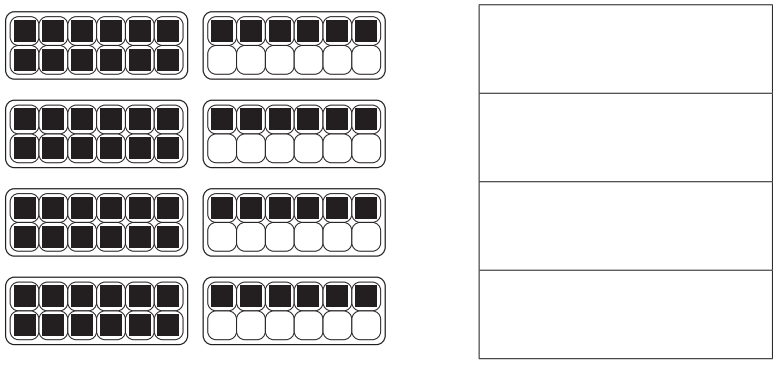
Answer:

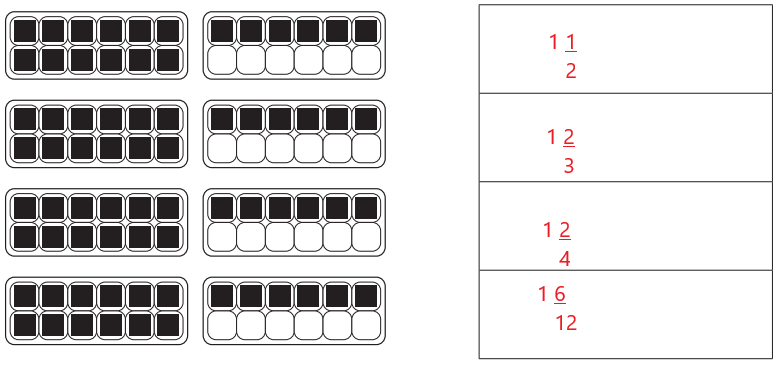
4 different ways to name a carton and a half of eggs 1$\frac{1}{2}$ , 1$\frac{2}{3}$, 1$\frac{2}{4}$ , 1$\frac{6}{12}$. Thus, the shaded regions are all indicated using a improper fraction.

Eggsploration Challenge

Question 1.
Jon’s dad brought home eggs in an 18-egg carton instead of a 12-egg carton. When Jon opened the carton three days later, there were only 12 eggs left in the carton. What fraction of the carton was still filled? Be sure to draw in the lines for string or yarn to show the number of equal parts into which you’re dividing the carton.

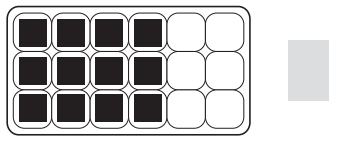
Answer:

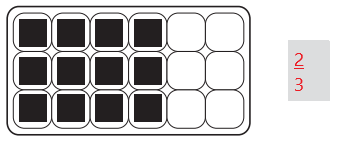
Jon’s dad brought home eggs in an 18-egg carton instead of a 12-egg carton.
The eggs left in the carton when Jon opened = 12
fraction = $\frac{2}{3}$

Question 2.
Figure out two other names for the fraction of the carton filled by 12 eggs. Be sure to draw in the lines for string or yarn to show the number of equal parts into which you’re dividing the carton.

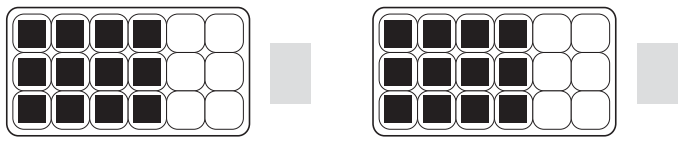
Answer:

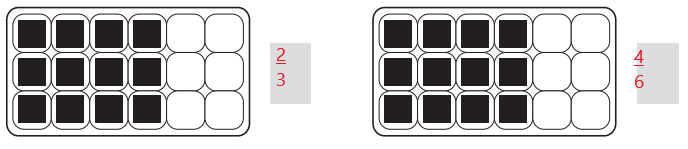
Other two names for the carton filling is $\frac{2}{3}$ and $\frac{4}{6}$.

Question 3.
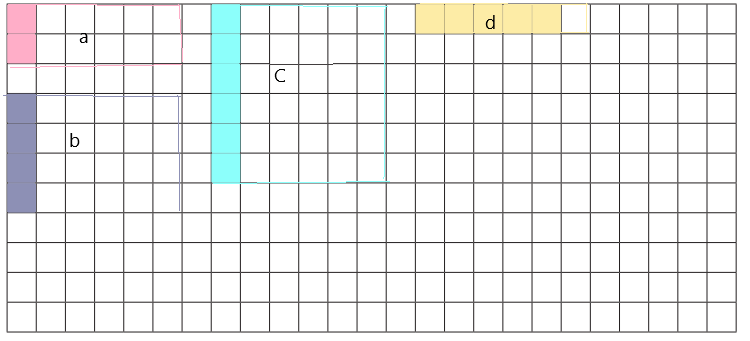
On a 12-egg carton, $\frac{1}{6}$ is 2 eggs. On the grid below, sketch 4 different cartons, in which:
a. $\frac{1}{6}$ is 2 eggs
b. $\frac{1}{6}$ is 4 eggs
c. $\frac{1}{6}$ is 6 eggs
d. $\frac{5}{6}$ is 5 eggs
On each carton you sketch, be sure to show the eggs and the yarn lines. Also, label each sketch with its letter.

Answer:

More Egg Carton Fractions

Question 1.
Write at least two fractions to show the part of each egg carton that is filled. Draw lines on the egg cartons to divide them into equal parts.

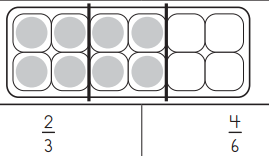
a.

Answer:

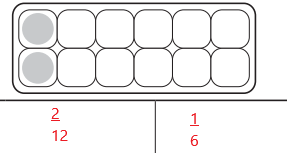
The shaded region can be represented in $\frac{2}{12}$ , $\frac{1}{6}$

b.

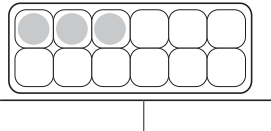
Answer:

The shaded region can be represented in $\frac{3}{12}$ , $\frac{1}{4}$

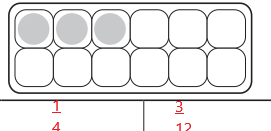
c.

Answer:

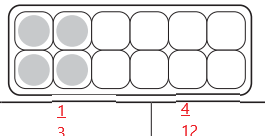
The shaded region can be represented in $\frac{4}{12}$ , $\frac{1}{3}$

d.

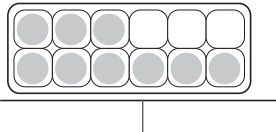
Answer:

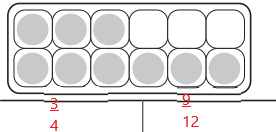
The shaded region can be represented in $\frac{9}{12}$ , $\frac{3}{4}$

e.

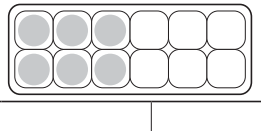
Answer:

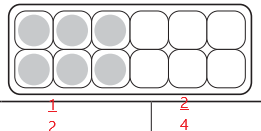
The shaded region can be represented in $\frac{1}{2}$ , $\frac{2}{4}$

Question 2.
Fractions can be greater than 1. If a fraction greater than 1 is writtten as a whole number with a fraction, it is called a mixed number. If it is written as a fraction, it is called an improper fraction. Draw on the egg cartons to divide them into equal parts. Then write a mixed number and an improper fraction to show how many full egg cartons are shown.