Bridges in Mathematics Grade 4 Student Book Unit 3 Module 2 Answer Key

Practicing the Bridges in Mathematics Grade 4 Student Book Answer Key Unit 3 Module 2 will help students analyze their level of preparation.

Bridges in Mathematics Grade 4 Student Book Answer Key Unit 3 Module 2

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 2 Session 1 Answer Key

Pizza Party Planning

A fourth grade class won a pizza party for collecting the most paper for recycling in their school contest. Medium pizzas were cut into 8 slices, and large pizzas were cut into 12 slices.

Question 1.
Mariah ate 2 slices of a large pizza. What fraction of the pizza did she eat? Draw a sketch to show your thinking.
Answer:  \(\frac{2}{12}\) or \(\frac{1}{6}\)
Given Mariah ate 2 slices of large pieces.
Total number of pieces in the large pizza = 12
therefore, the fraction of pizza she ate = \(\frac{1}{6}\) or \(\frac{2}{12}\)

Question 2.
Carlos said that Mariah ate of \(\frac{1}{6}\) a pizza. Tell why you agree or disagree.
Answer: Yes. I agree with Carlos
Given Mariah ate 2 slices of large pieces.
Total number of pieces in the large pizza = 12
therefore, the fraction of pizza she ate = \(\frac{1}{6}\) or \(\frac{2}{12}\)

Question 3.
Mariah’s table seats 4 students. Each student ate 2 slices of a large pizza. Write an equation that shows what fraction of a pizza was eaten at Mariah’s table.
Answer:  \(\frac{8}{12}\)
Mariah’s table seats 4 students.
Each student ate 2 slices of a large pizza.
Therefore, the fraction of a pizza was eaten at Mariah’s table = \(\frac{2}{12}\) + \(\frac{2}{12}\) + \(\frac{2}{12}\) + \(\frac{2}{12}\)
= \(\frac{8}{12}\)

Question 4.
Tony ate 3 slices of a medium pizza. His friend, Connor, ate 4 slices of the same pizza.

a. Write two different fractions to describe how much pizza Connor ate.
Answer: \(\frac{2}{4}\), \(\frac{4}{8}\)
Total number of pieces in medium pizza = 8
Connor ate 4 slices.
Therefore, the two different fractions to describe the amount of pizza ate by  Connor is \(\frac{2}{4}\), \(\frac{4}{8}\).

b. What fraction of the pizza did the boys eat together? _________
Answer: \(\frac{7}{4}\)
Total number of pieces in medium pizza = 8
number of pieces in medium pizza did the boys eat together = 7
Therefore, the fractions to describe the number of pieces in medium pizza did the boys eat together \(\frac{7}{4}\).

Question 5.
Lionel’s table group drank 1\(\frac{1}{2}\) liters of juice with their pizza. How many milliliters did they drink? Show your work.
Answer: 1500 ml
1 liter = 1000 ml
Lionel’s table group drank 1\(\frac{1}{2}\) liters of juice
= \(\frac{3}{2}\)  = 1.5 liters
1.5 liters = 1.5 x 1000 ml
= 1500 ml

Question 6.
Complete the problems.

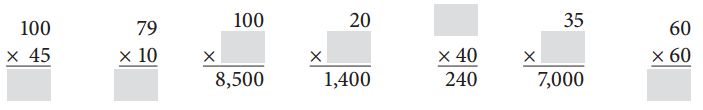
Answer:

Multiplication was performed for the above given problems.
If two numbers are given, we need to multiply both the numbers to get the result.
When a number and the result, which is the product of two numbers are given, then divide the resulted product with the give number to get another number.

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 2 Session 2 Answer Key

Last Equation Wins

Player 1 ________ Player 2 _______

Player 1 _______ Player 2 ______

What’s the share?

Question 1.
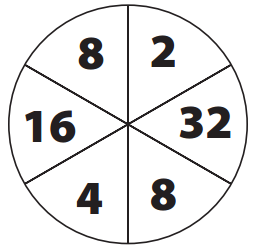
If the area of the largest square on the geoboard is 1, what is the area of each region?

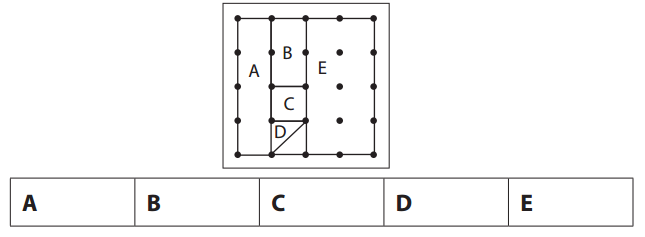
Answer:

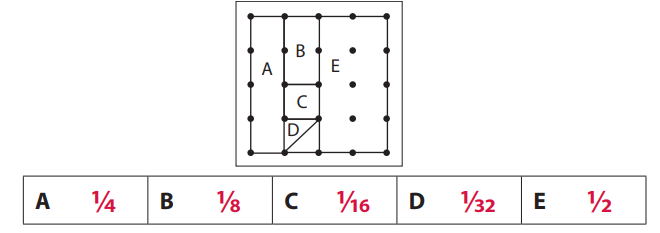
16 squares can be formed by joining the dots given above.
A. A has 4 parts. So 4 divided by total 16 squares = \(\frac{4}{16}\) = \(\frac{1}{4}\)
B. B has 2 parts. So 2 divided by total 16 squares = \(\frac{2}{16}\) = \(\frac{1}{8}\)
C. C has 1 part. So 1 divided by total 16 squares = \(\frac{1}{16}\)
D. D has half part. So divide that part by 16 = \(\frac{1}{32}\)
E. E has 8 parts. So 8 divided by total 16 squares = \(\frac{8}{16}\) = \(\frac{1}{2}\)

Question 2.
Write four statements and matching fraction equations that compare two regions.

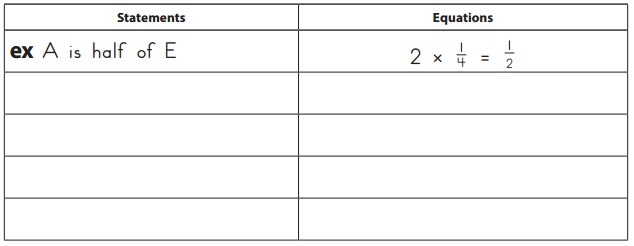
Answer:

i) B is twice as big as C = 2 x \(\frac{1}{16}\) = \(\frac{1}{8}\)
ii) B is one-fourth of E = 4 x \(\frac{1}{8}\) = \(\frac{1}{2}\)
iii) 4 Cs fi into A = \(\frac{1}{16}\) + \(\frac{1}{16}\)  + \(\frac{1}{16}\) + \(\frac{1}{16}\) = \(\frac{1}{4}\)
iv) D is half of C = \(\frac{1}{32}\)  + \(\frac{1}{32}\) = \(\frac{1}{16}\)

Question 3.
Fill in the blank with the correct relational symbol: <, >, or =.

Answer:

\(\frac{1}{2}\)  > \(\frac{1}{6}\)
\(\frac{3}{4}\)  > \(\frac{3}{8}\)
\(\frac{4}{9}\)  < \(\frac{6}{9}\)
\(\frac{4}{8}\)  = \(\frac{5}{10}\)

Question 4.
List all the factor pairs for the number 32.
Answer: 1, 2, 4, 8, 16, 32
Factors are the ones which will divide the number and leaves remainder as zero. 1, 2, 4, 8, 16, 32 divides the number  and leaves the remainder as zero.

Question 5.
List three prime numbers greater than 20.
Answer: 23, 29, 31
Prime numbers are the ones having factors as one and the number itself. The numbers which are greater than 20 and prime numbers are 23, 29, 31. Because the factors of these numbers are 1 and the number itself.

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 2 Session 3 Answer Key

Comparing, Adding & Subtracting Fractions

Question 1.
Use the symbols >, =, < to compare each pair of fractions.

Answer:

\(\frac{3}{8}\) > \(\frac{2}{8}\)
\(\frac{3}{8}\) > \(\frac{1}{4}\)
\(\frac{3}{8}\) < \(\frac{7}{16}\)
\(\frac{7}{16}\) > \(\frac{1}{4}\)
\(\frac{1}{4}\) < \(\frac{3}{4}\)
\(\frac{4}{16}\) > \(\frac{2}{16}\)
\(\frac{4}{16}\) < \(\frac{5}{8}\)
\(\frac{3}{4}\) < \(\frac{5}{8}\)

Question 2.
Find each sum.

Answer:

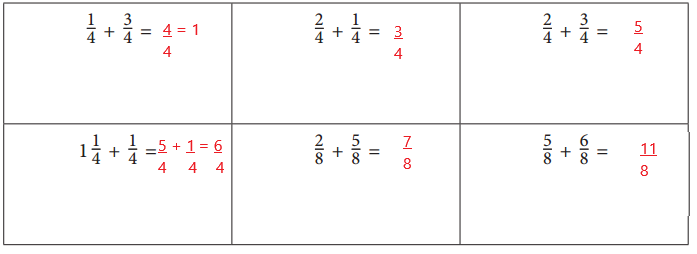
\(\frac{1}{4}\) + \(\frac{3}{4}\) = \(\frac{4}{4}\) = 1
\(\frac{2}{4}\) + \(\frac{1}{4}\) = \(\frac{3}{4}\)
\(\frac{2}{4}\) + \(\frac{3}{4}\) = \(\frac{5}{4}\)
1\(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{6}{4}\)
\(\frac{2}{8}\) + \(\frac{5}{8}\) = \(\frac{7}{8}\)
\(\frac{5}{8}\) + \(\frac{6}{8}\) = \(\frac{11}{8}\)

Question 3.
Find each difference.

Answer:

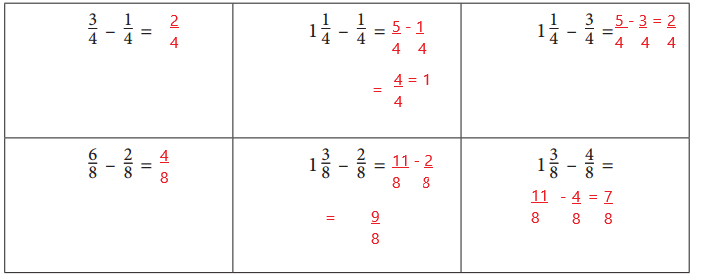
\(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{2}{4}\)
1\(\frac{1}{4}\) – \(\frac{1}{4}\) = 1
1\(\frac{1}{4}\) – \(\frac{3}{4}\) = \(\frac{2}{4}\)
\(\frac{6}{8}\) – \(\frac{2}{8}\) = \(\frac{4}{8}\)
1\(\frac{3}{8}\) – \(\frac{2}{8}\) = \(\frac{9}{8}\)
1\(\frac{3}{8}\) – \(\frac{4}{8}\) = \(\frac{7}{8}\)

Question 4.
CHALLENGE Write as many equivalent fractions as you can for each fraction shown below.

Answer:

The equivalent fractions for \(\frac{1}{8}\) are \(\frac{2}{16}\), \(\frac{3}{24}\), \(\frac{4}{32}\), \(\frac{5}{40}\), \(\frac{6}{48}\), \(\frac{7}{56}\), \(\frac{8}{64}\), \(\frac{9}{72}\)
The equivalent fractions for \(\frac{1}{4}\) are \(\frac{2}{8}\), \(\frac{3}{12}\), \(\frac{4}{16}\), \(\frac{5}{20}\), \(\frac{6}{24}\), \(\frac{7}{28}\), \(\frac{8}{32}\), \(\frac{9}{36}\)
The equivalent fractions for \(\frac{2}{3}\) are \(\frac{4}{6}\), \(\frac{6}{9}\), \(\frac{8}{12}\), \(\frac{10}{15}\), \(\frac{12}{18}\), \(\frac{14}{21}\), \(\frac{16}{24}\)

d. Describe how you can write equivalent fractions for any fraction.
Answer:
The equivalent fraction for any number can be written by multiplying both numerator and denominator with the same number.
For Example, the equivalent fraction for  \(\frac{2}{3}\) can be obtained by multiplying both numerator and denominator with 2, which is \(\frac{4}{6}\)

Question 5.
CHALLENGE Find each sum.

Answer:

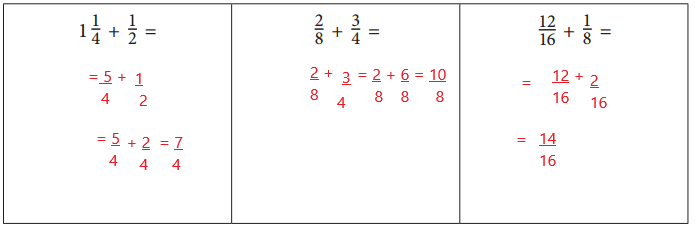
1\(\frac{1}{4}\) + \(\frac{1}{2}\) = \(\frac{7}{4}\)
\(\frac{2}{8}\) + \(\frac{3}{4}\) = \(\frac{10}{8}\)
\(\frac{12}{16}\) + \(\frac{1}{8}\) = \(\frac{14}{16}\)

Question 6.
CHALLENGE Find each difference.

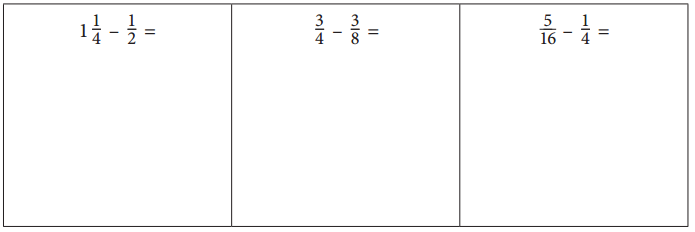
Answer:

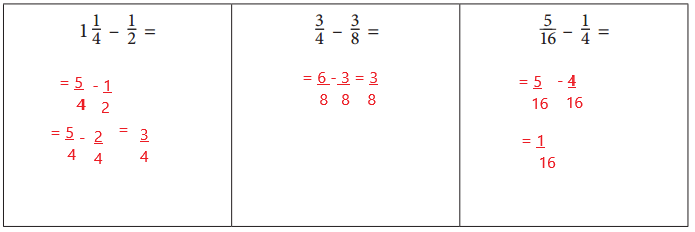
1\(\frac{1}{4}\) – \(\frac{1}{2}\) = \(\frac{3}{4}\)
\(\frac{3}{4}\) – \(\frac{3}{8}\) = \(\frac{3}{8}\)
\(\frac{5}{16}\) – \(\frac{1}{4}\) = \(\frac{1}{16}\)

Adding & Subtracting Fractions

Ariel got a new box of 8 crayons and a set of 10 markers for her birthday. Use this information as you solve each problem below. Use numbers, labeled sketches, or words to show your thinking.

Question 1.
Ariel used 5 crayons to make a thank-you card. What fraction of the box did she use?
Answer: \(\frac{5}{8}\) of the box
Number of crayons used by Ariel  to make a thank-you card = 5
Ariel got a new box with total crayons = 8
Therefore, the fraction of the box = \(\frac{5}{8}\)

Question 2.
Ariel gave her brother 4 crayons. What fraction does she have left out of her box of 8?
Answer: \(\frac{4}{8}\)
Number of crayons gave her brother  = 4
Ariel got a new box with total crayons = 8
Therefore, the fraction of the box = \(\frac{4}{8}\)

Question 3.
After she gave some crayons to her brother, Ariel’s dog ate 2 of her crayons.

a. Now what fraction does Ariel have left of her original box of 8 crayons?
Answer: \(\frac{2}{8}\)  or \(\frac{1}{4}\)  of the box
Ariel’s dog ate 2 of her crayons.
Ariel got a new box with total crayons = 8
Therefore, the fraction of the box = \(\frac{2}{8}\)

b. What fraction of the crayons went to Ariel’s brother and her dog?
Answer: \(\frac{6}{8}\) or \(\frac{3}{4}\) of the box
crayons went to Ariel’s brother and her dog = 6
Ariel got a new box with total crayons = 8
Therefore, the fraction of the box = \(\frac{6}{8}\)

Question 4.
Ariel took 6 markers out of her marker set. What fraction of the markers are left in the set?
Answer: \(\frac{4}{10}\) or \(\frac{2}{5}\) of the markers
Ariel took 6 markers out of her marker set
Ariel got a new box with total crayons = 8
Therefore, the fraction of the box = \(\frac{4}{10}\)

Question 5.
Two of Ariel’s markers are green, 2 are red, and 3 are blue. What fraction of the markers are
green? __________
red? __________
blue? _________
Answer:
Two of Ariel’s markers are green, 2 are red, and 3 are blue.
Total markers = 10
green? \(\frac{2}{10}\)  or \(\frac{1}{5}\)
red? \(\frac{2}{10}\)  or \(\frac{1}{5}\)
blue? \(\frac{3}{10}\)

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 2 Session 4 Answer Key

Introducing Dozens of Eggs

Work Place Instructions 3A Dozens of Eggs

Each pair of players needs:

• 2 Dozens of Eggs Record Sheets
• 1 deck of Dozens of Eggs Fraction Cards
• 1 Egg Carton Diagram
• 6 pieces of string or yarn
• 12 colored tiles
• colored pencils or crayons

1. Players shuffle the fraction cards and lay them face-down in a stack. Each player draws one card. The player with the larger fraction goes first. The cards just drawn go at the bottom of the stack.
Players may build fractions on the Egg Carton Diagram if needed to determine which fraction is larger.
2. Player 1 draws a card from the top of the deck, reads the fraction out loud, and uses string and colored tiles to build a model of the fraction on the Egg Carton Diagram. Player 2 checks Player 1’s work.

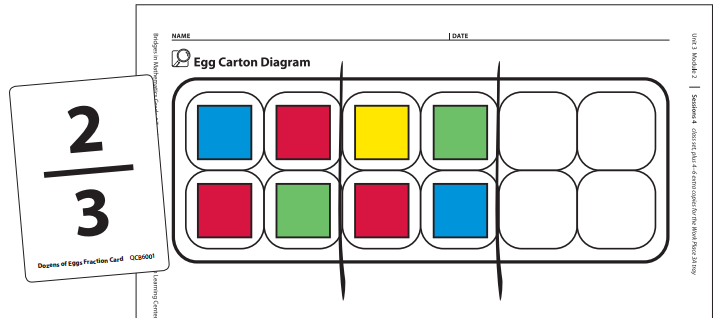
Jasmine Wow! I got a really big fraction on my first turn. So I’m going to divide the egg carton into 3 equal parts, and fill 2 of them, like this.
Sara I agree that \(\frac{2}{3}\) of the egg carton is 8 eggs, because I know that there are 4 eggs in one-third of a carton.
3. Player 1 draws circles to represent that number of eggs in one of the diagrams on her record sheet and records that number of twelfths as a fraction on the sheet.

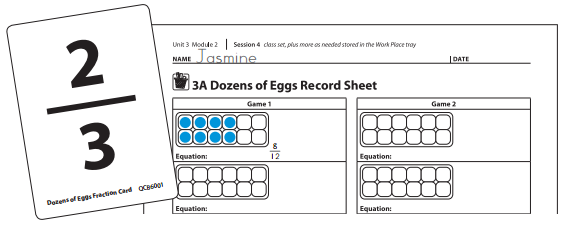
Jasmine I have to change \(\frac{2}{3}\) into twelfths, but that’s easy, because each egg is one-twelfth of the carton, so I got \(\frac{8}{12}\) on my first turn. I only need 4 more twelfths to fill this carton.
4. Player 1 empties the egg carton diagram and puts the card in a discard stack. Then Player 2 takes a turn.
5. Players continue to take turns until one person has filled in all four cartons on the record sheet. Players should use a different color to record each new turn.
When all the cards in the deck have been used, shuffle the deck and use it again.
6. On each turn, players must put all of the eggs in one carton. However, players may begin to fill another carton before the first is completely filled.
7. If the fraction drawn does not fit into one of the cartons, the player misses that turn.
8. When a carton is filled, the player writes an equation by inserting plus signs between the fractions for that carton and showing them equal to 1 whole.

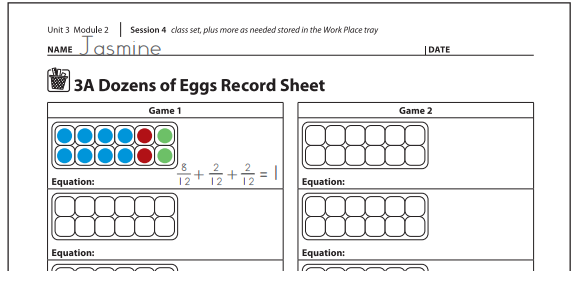
9. The winner is the first player to fill all four cartons on his record sheet. If Player 1 is the first to fill all four cartons, Player 2 may take one last turn.

Game Variations

A. Players work together to fill all four cartons on a single record sheet rather than playing against each other.
B. Players begin with all four cartons filled, by drawing 12 circles in each of the cartons and writing at
the start of each equation line. Then each player subtracts the fractions that are written on the cards they get, crossing out that many eggs and subtracting that many twelfths. Players must subtract the entire fraction from one carton rather than splitting the fraction between two or more cartons. The winner is the first player to get rid of all the eggs from all four cartons.

Egg Carton Fractions

Question 1.
Solve the following multiplication and division problems. They might help you think about the egg cartons in problem 2.
12 ÷ 2 = ____ 12 ÷ 3 = ____ 12 ÷ 4 = ____ 12 ÷ 6 = ______
6 × 3 = ____ 4 × 2 = ____ 3 × 3 = ____ 2 × 5 = ______
Answer:
12 ÷ 2 = 6
12 ÷ 3 = 4
12 ÷ 4 = 3
12 ÷ 6 = 2
6 × 3 = 18
4 × 2 =8
3 × 3 = 9
2 × 5 = 10

Question 2.
Write a fraction to show the amount of each egg carton that is filled with eggs. (The cartons are divided into equal parts for you.) Then write an equivalent fraction with 12 in the denominator.
ex

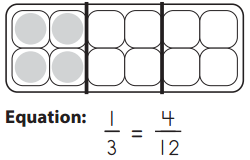
a.

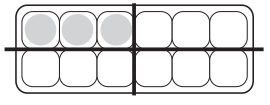
Answer: \(\frac{1}{4}\)  = \(\frac{3}{12}\)

b.

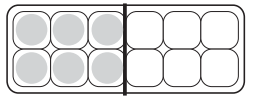
Answer: \(\frac{1}{2}\)  = \(\frac{6}{12}\)

c.

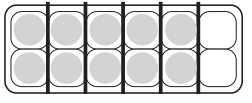
Answer: \(\frac{5}{6}\)  = \(\frac{10}{12}\)

d.

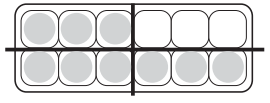
Answer: \(\frac{3}{4}\)  = \(\frac{9}{12}\)

e.

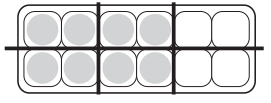
Answer: \(\frac{4}{6}\)  = \(\frac{8}{12}\)

Question 3.
Use the symbols, >, =, or < to compare each pair of fractions.

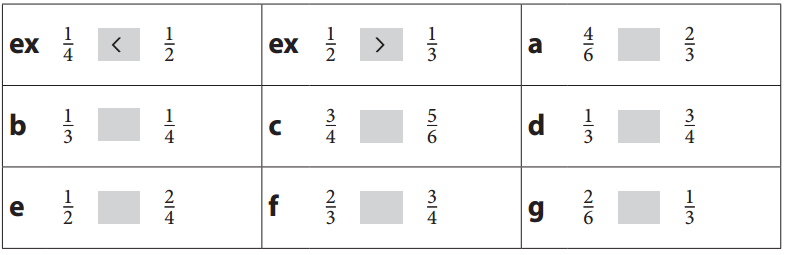
Answer:

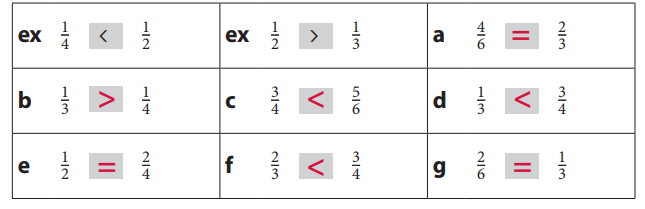
a. \(\frac{4}{6}\) = \(\frac{2}{3}\)
b. \(\frac{1}{3}\) > \(\frac{1}{4}\)
c. \(\frac{3}{4}\) < \(\frac{5}{6}\)
d. \(\frac{1}{3}\)< \(\frac{3}{4}\)
e. \(\frac{1}{2}\) = \(\frac{2}{4}\)
f. \(\frac{2}{3}\) < \(\frac{3}{4}\)
g. \(\frac{2}{6}\) = \(\frac{1}{3}\)

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 2 Session 5 Answer Key

How Many Candy Bars?

Question 1.
Mrs. Wiggens is hosting her annual class picnic. She wants to give each student 3/4 of a candy bar for a dessert treat.
a. How many candy bars will she need for two students? __________
Answer:  \(\frac{6}{4}\)
Mrs. Wiggens wants to give each student 3/4 of a candy bar for a dessert treat.
Therefore, the number of candy bars that she will need for two students = \(\frac{6}{4}\)

b. How many candy bars will she need for four students? _______
Answer: \(\frac{12}{4}\) = 3
Mrs. Wiggens wants to give each student 3/4 of a candy bar for a dessert treat.
Therefore, the number of candy bars that she will need for two students = \(\frac{12}{4}\) = 3

c. In order to make things easier for Mrs. Wiggens, fill in the chart below so she will know how many candy bars she might need.

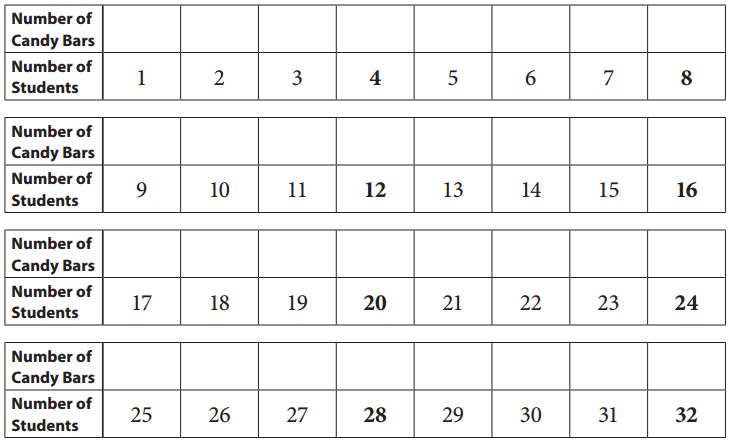
Answer:

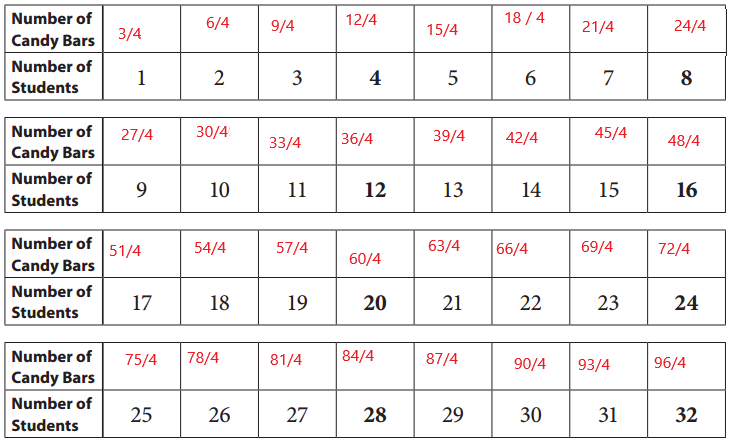
The number of candybars for 1 to 32 students can be calculated by adding 3 to the numerator of every share of candy bar to each student.

Question 2.
How did you get your answers on the chart above? Use numbers, words, or labeled sketches to describe your strategy.
Answer:
Mrs. Wiggens wants to give each student 3/4 of a candy bar for a dessert treat.
So number of students that get number of candy bars  = number of students * each student get candy

Question 3.
CHALLENGE What kind of general rule could you give Mrs. Wiggens to know how many candy bars to get no matter how many students she has?
Answer:
Mrs. Wiggens wants to give each student 3/4 of a candy bar for a dessert treat.
So number of students that get number of candy bars  = number of students * each student get candy

Fractions & Mixed Numbers

Question 1.
The circles below are divided into equal parts. Write two fractions to show what part of each circle is filled in.

ex

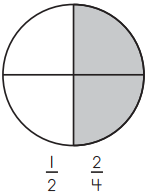
a.

Answer: \(\frac{1}{4}\) \(\frac{2}{8}\)
Total number of parts = 8
Number of shaded parts = 2
Therefore, the two fractions that show the part of each circle are \(\frac{1}{4}\), \(\frac{2}{8}\)

b.

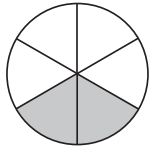
Answer: \(\frac{6}{8}\) \(\frac{3}{4}\)
Total number of parts = 8
Number of shaded parts = 6
Therefore, the two fractions that show the part of each circle are \(\frac{6}{8}\), \(\frac{3}{4}\)

c.

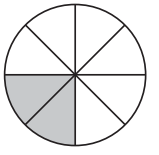
Answer: \(\frac{1}{3}\) \(\frac{2}{6}\)
Total number of parts = 6
Number of shaded parts = 2
Therefore, the two fractions that show the part of each circle are \(\frac{2}{6}\), \(\frac{1}{3}\)

d.

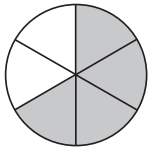
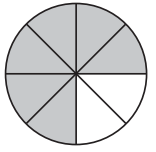
Answer: \(\frac{2}{3}\), \(\frac{4}{6}\)
Total number of parts = 6
Number of shaded parts = 4
Therefore, the two fractions that show the part of each circle are \(\frac{4}{6}\), \(\frac{2}{3}\)

e.

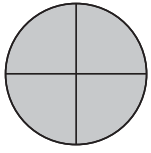
Answer: \(\frac{1}{1}\) \(\frac{4}{4}\)
Total number of parts = 4
Number of shaded parts = 4
Therefore, the two fractions that show the part of each circle are \(\frac{4}{4}\), \(\frac{1}{1}\)

Question 2.
The circles below are divided into equal parts. Write a fraction and a mixed number to show how many circles are filled in.

Answer:

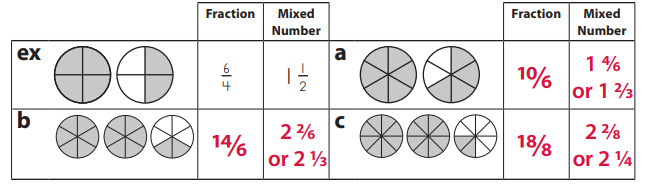
a. there are 10 colored parts in the given picture, so the result is \(\frac{10}{6}\) = 1\(\frac{2}{3}\)
b. there are 14 colored parts in the given picture, so the result is \(\frac{14}{6}\) = 2\(\frac{1}{3}\)
c. there are 18 colored parts in the given picture, so the result is \(\frac{18}{8}\) = 2\(\frac{2}{8}\)

Question 3.
Fill in the missing fractions or mixed numbers.

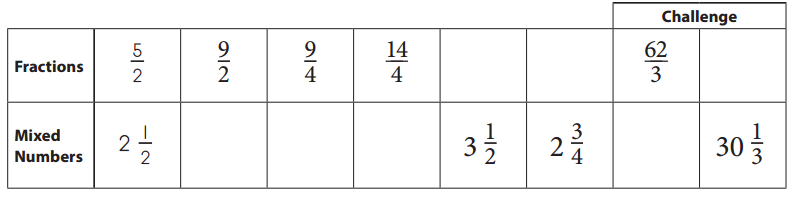
Answer:

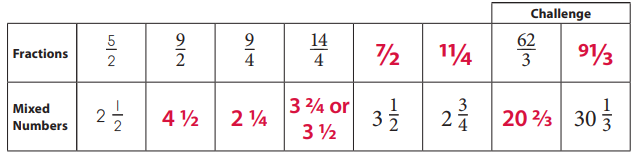
\(\frac{5}{2}\) = 2\(\frac{1}{2}\)
\(\frac{9}{2}\) =4\(\frac{1}{2}\)
\(\frac{9}{4}\) = 2\(\frac{1}{4}\)
\(\frac{14}{4}\) = 3\(\frac{1}{2}\)
\(\frac{7}{2}\) = 3\(\frac{1}{2}\)
\(\frac{11}{2}\) = 2\(\frac{3}{4}\)
\(\frac{62}{3}\) = 20\(\frac{2}{3}\)
\(\frac{91}{3}\) =30\(\frac{1}{3}\)

Bridges in Mathematics Grade 4 Student Book Unit 3 Module 2 Session 6 Answer Key

Work Place Instructions 3B Racing Fractions

Each pair of players needs:

• 1 Racing Fractions Record Sheet to share
• 1 Racing Fractions Game Board
• 7 red game markers
• 7 blue game markers
• 1 deck of Racing Fraction Cards

1. Players decide who will play with the red game markers, and who will play with the blue markers. Then both players place one of their game markers at the beginning of each number line on the game board.
2. Players shuffle the fraction cards and lay them face-down in a stack. Each player draws one card. The player with the larger fraction goes first. Players put the cards just drawn at the bottom of the stack.
3. Player 1 draws a new card and moves one or more game markers the distance shown on the card.
Player 1 I got \(\frac{3}{6}\). That’s the same as \(\frac{1}{2}\), so I could go \(\frac{1}{2}\), \(\frac{2}{4}\), \(\frac{3}{6}\), \(\frac{4}{8}\), or \(\frac{5}{10}\). Hmm…or I could do \(\frac{1}{3}\) and \(\frac{1}{6}\). I remember those make \(\frac{1}{2}\) from when we looked at egg carton fractions. I think I’ll do that.

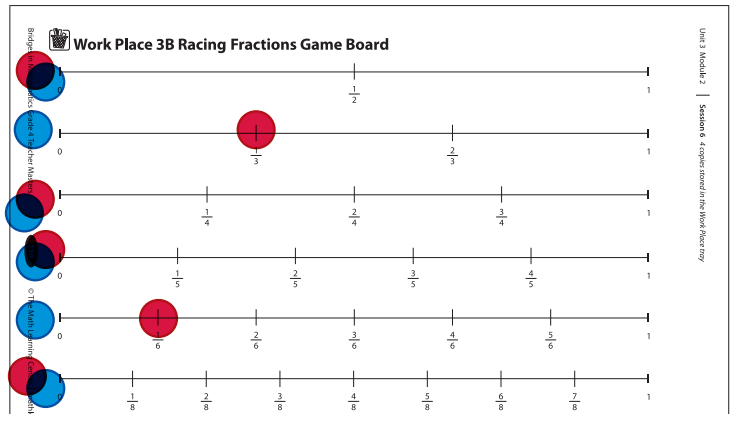
4. Player 1 records the fraction in his Fraction column on the record sheet and writes the fraction or equation that describes how the game markers were moved in his Equation column.
(If the player selected \(\frac{1}{2}\) and moved \(\frac{1}{2}\), he would write \(\frac{1}{2}\). If the player selected \(\frac{1}{2}\) and moved one marker to \(\frac{1}{3}\) and another marker to \(\frac{1}{6}\), he would write \(\frac{1}{3}\) + \(\frac{1}{6}\) = \(\frac{1}{2}\).)
5. Player 2 checks first player’s work on the record sheet. Player 3 tries again if an error was made.
6. Then Player 2 draws a fractions card and takes a turn. Player 3 checks the second player’s work.
7. Players continue to take turns, record moves, and check each other’s work until one player’s game markers are all on 1. If Player 1 is the first to land on 1, Player 2 may take one last turn.
If a player cannot find a possible move for a card he has drawn, the player loses the turn.
Players may also move game markers backward. For example, if a player selects \(\frac{1}{3}\), she can move one marker up \(\frac{1}{2}\) and another back \(\frac{1}{6}\). The sum or the difference of the moves still needs to equal the value on the fraction card.

Game Variations

A. Play cooperatively. Players can work together and help each other finish the track in a certain time period.
B. Double the length of each track by taping 2 copies of the Racing Fractions Game Board Teacher Master together, writing a 3 in front of every fraction on the second sheet, and changing the 3 at the end of each track on the second sheet to a 2.

Understanding Fractions & Mixed Numbers

Question 1.
Sketch and label a picture that represents 1\(\frac{1}{2}\).
Answer:

Question 2.
Answer each question below:
a. How many halves are in \(\frac{3}{2}\)? _____
Answer: 3
Therefore, the number of halves that are in \(\frac{3}{2}\) is 3.

b. How many fourths are in \(\frac{7}{4}\) ? _____
Answer: 7
Therefore, the number of fourths that are in \(\frac{7}{4}\) is 7.

c. How many thirds are in \(\frac{8}{3}\) ? _____
Answer: 8
Therefore, the number of thirds that are in \(\frac{8}{3}\) is 8.

d. How many fifths are in \(\frac{6}{5}\) ? _______
Answer: 6
Therefore, the number of fifths that are in \(\frac{6}{5}\) is 6.

e. What do you notice about problems a—d?
Answer: The numerator tells how many parts there are in each fraction.
The number of halves that are in \(\frac{3}{2}\) is 3.
The number of fourths that are in \(\frac{7}{4}\) is 7.
The number of thirds that are in \(\frac{8}{3}\) is 8.
The number of fifths that are in \(\frac{6}{5}\) is 6.

Question 3.
Write each fraction as a mixed number. Make a drawing, if needed.
a. \(\frac{5}{2}\) = ______
b. \(\frac{7}{6}\) = ______
c. \(\frac{4}{3}\) = ______
d. \(\frac{12}{8}\) = ______
Answer:
\(\frac{5}{2}\) =  2\(\frac{1}{2}[/latex
[latex]\frac{7}{6}\) = 1\(\frac{1}{6}\)
\(\frac{4}{3}\) = 1\(\frac{1}{3}\)
\(\frac{12}{8}\) = 1\(\frac{4}{8}\)

Question 4.
Write each mixed number as a fraction. Make a drawing, if needed.
a. 1\(\frac{2}{3}\) = ______
b. 1\(\frac{3}{5}\) = ______
c. 2\(\frac{1}{4}\) = ______
d. 3\(\frac{1}{2}\) = ______
Answer:
1\(\frac{2}{3}\) = \(\frac{5}{3}\)
1\(\frac{3}{5}\) = \(\frac{8}{5}\)
2\(\frac{1}{4}\) = \(\frac{9}{4}\)
3\(\frac{1}{2}\) = \(\frac{7}{2}\)