Bridges in Mathematics Grade 3 Student Book Unit 7 Module 1 Answer Key

The solutions to Bridges in Mathematics Grade 3 Student Book Answer Key Unit 7 Module 1 can help students to clear their doubts quickly.

Bridges in Mathematics Grade 3 Student Book Answer Key Unit 7 Module 1

Bridges in Mathematics Grade 3 Student Book Unit 7 Module 1 Session 1 Answer Key

Skills Review: Area, Multiplication & Fractions

Question 1.
Determine the area of each rectangle and write an equation to match.
ex:

3 × 7 = 21

a.

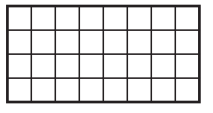
Answer:
Area of rectangle = 32.

Explanation:
Number of row = 4.
Number of columns = 8.
Area of rectangle = Number of row × Number of columns
= 4 × 8
= 32.

b.

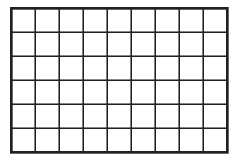
Answer:
Area of rectangle = 54.

Explanation:
Number of row = 6.
Number of columns = 9.
Area of rectangle = Number of row × Number of columns
= 6 × 9
= 54.

c.

Answer:
Area of rectangle = 28.

Explanation:
Number of row = 4.
Number of columns = 7.
Area of rectangle = Number of row × Number of columns
= 4 × 7
= 28.

Question 2.
Fill in the missing numbers below.

Answer:

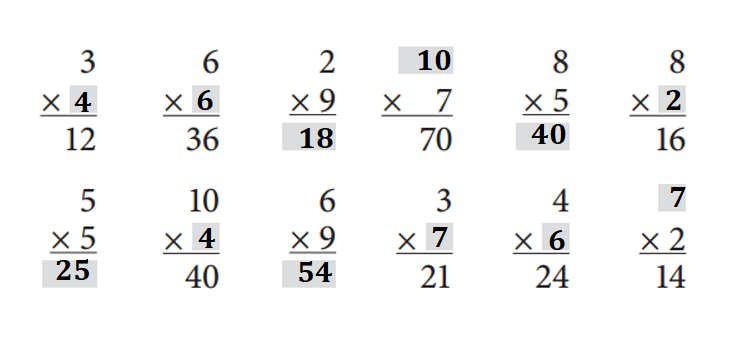
Explanation:
Given Equations:
3 × ?? = 12.
=> ?? = 12 ÷ 3
=> ?? = 4.
6 × ?? = 36.
=> ?? = 36 ÷ 6
=> ?? = 6.
2 × 9 = ??
=> 2 × 9 = 18.
?? × 7 = 70.
8 × 5 = ??
=> 8 × 5 = 40.
8 × ?? = 16.
=> ?? = 16 ÷ 8
=> ?? = 2.
5 × 5 = ??
=> 5 × 5 = 25.
10 × ?? = 40.
=> ?? = 40 ÷ 10
=> ?? = 4.
6 × 9 = ??
=> 6 × 9 = 54.
3 × ?? = 21.
=> ?? = 21 ÷ 3
=> ?? = 7.
4 × ?? = 24.
=> ?? = 24 ÷ 4
=> ?? = 6.
?? × 2 = 14.
=> ?? = 14 ÷ 2
=> ?? = 7.

Question 3.
CHALLENGE Solve each equation.
16 + 25 – (6 × 4) = ______________
(7 × 7) + 175 = _______________
(10 × 9) – 65 = _______________
Answer:
Equation:
16 + 25 – (6 × 4) = ______________
(7 × 7) + 175 = _______________
(10 × 9) – 65 = _______________

Explanation:
Given Equation:
16 + 25 – (6 × 4) = ??
=> 41 – (6 × 4) = ??
=> 41 – 24 = ??
=> 17 = ??
(7 × 7) + 175 = ??
=> 49 + 175 = ??
=> 224 = ??
(10 × 9) – 65 = ??
=> 90 – 65 = ??
=> 25 = ??

Question 4.
Place the following fractions on the number line below: \(\frac{1}{4}\), 1, \(\frac{3}{4}\), \(\frac{3}{8}\), 0, \(\frac{8}{8}\), \(\frac{5}{8}\), \(\frac{4}{8}\)

Answer:

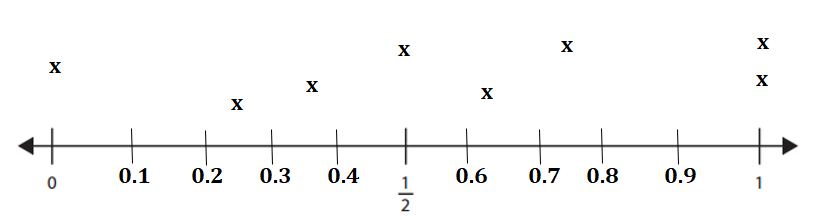
Explanation:
Given Fractions on the number line:
\(\frac{1}{4}\) = 0.25.
1
\(\frac{3}{4}\) = 0.75.
\(\frac{3}{8}\) = 0.375.
0
\(\frac{8}{8}\) = 1.
\(\frac{5}{8}\) = 0.625.
\(\frac{4}{8}\) = \(\frac{1}{2}\) = 0.50.

Bridges in Mathematics Grade 3 Student Book Unit 7 Module 1 Session 2 Answer Key

More Stickers & Beads

Question 1.
Sara bought a sheet of stickers with 2 rows of 5 stickers on it. The stickers cost 6 cents each. How much did Sara pay for the entire sheet of stickers?
a. What is this problem asking you to figure out?
Answer:
This problem asking you to figure out how much she needs to pay in all to the stickers.
Cost of Sara pays for the entire sheet of stickers = 60 cents.

Explanation:
Number of rows Sara bought a sheet of stickers = 2.
Number of stickers on it = 5.
Cost of stickers each = 6 cents.
Cost of Sara pays for the entire sheet of stickers = (Number of rows Sara bought a sheet of stickers × Number of stickers on it) × Cost of stickers each
= (2 × 5) × 6 cents
= 10 × 6 cents
= 60 cents.

b. Write an equation for the problem. Use a letter to stand for the unknown quantity.
Answer:
Cost of Sara pays for the entire sheet of stickers (m) = (Number of rows Sara bought a sheet of stickers × Number of stickers on it) × Cost of stickers each = 60 cents.

Explanation:
Number of rows Sara bought a sheet of stickers = 2.
Number of stickers on it = 5.
Cost of stickers each = 6 cents.
Cost of Sara pays for the entire sheet of stickers (m) = (Number of rows Sara bought a sheet of stickers × Number of stickers on it) × Cost of stickers each
= (2 × 5) × 6 cents
= 10 × 6 cents
= 60 cents.

c. Solve the problem. Show all your work including numbers, words, or labeled sketches.
Sara paid ____________ for the entire sheet of stickers.
Answer:
Cost of Sara pays for the entire sheet of stickers (m) = 60 cents.
Sara paid 60 cents for the entire sheet of stickers.

Question 2.
Jonah bought a sheet of stickers with 5 rows of 8 stickers on it. He gave 12 of the stickers to his little sister. How many stickers did he have left?
a. What is this problem asking you to figure out?
Answer:
This problem is asking you to figure out about the stickers he have left.

Explanation:
Number of stickers of rows Jonah bought a sheet = 5.
Number of stickers on it = 8.
Number of stickers he gave to his little sister = 12.
Number of stickers he have left = (Number of stickers of rows Jonah bought a sheet × Number of stickers on it) – Number of stickers he gave to his little sister
= (5 × 8) – 12
= 40 – 12
= 28.

b. Write an equation for the problem. Use a letter to stand for the unknown quantity.
Answer:
Equation:
Number of stickers he have left (m) = (Number of stickers of rows Jonah bought a sheet × Number of stickers on it) – Number of stickers he gave to his little sister
= (5 × 8) – 12 = 28.

Explanation:
Number of stickers of rows Jonah bought a sheet = 5.
Number of stickers on it = 8.
Number of stickers he gave to his little sister = 12.
Number of stickers he have left (m) = (Number of stickers of rows Jonah bought a sheet × Number of stickers on it) – Number of stickers he gave to his little sister
= (5 × 8) – 12
= 40 – 12
= 28.

c. Solve the problem. Show all your work including numbers, words, or labeled sketches.
Jonah had ______________ stickers left.
Answer:
Number of stickers he have left (m) = 28.
Jonah had 28 stickers left.

Question 3.
Jasmine and her mother bought 2 boxes of beads to make some necklaces. One box was divided into 6 sections, with 10 beads in each section. The other box was divided into 4 sections, with 9 beads in each section. How many beads did they get in all?
a. What is this problem asking you to figure out?
Answer:
This problem is asking you to figure out the total beads they get in all.

Explanation:
Number of boxes of beads to make some necklaces Jasmine and her mother bought = 2.
Number of sections one box was divided = 6.
Number of beads in each section of one box = 10.
Number of sections other box was divided = 4.
Number of beads in each section of other box = 9.
Number of beads they get in all = (Number of sections one box was divided × Number of beads in each section of one box) + (Number of sections other box was divided × Number of beads in each section of other box)
= (6 × 10) + (4 ×9)
= 60 + 49
= 109.

b. Which equation best represents this problem? (The letter b stands for beads in all the equations below.)
(6 × 10) + (4 × 9) = b
(6 × 10) – (4 × 9) = b
2 + 6 + 10 + 4 + 9 = b
2 × (6 × 10) = b
Answer:
Equation best represents this problem:
(6 × 10) + (4 × 9) = b.

Explanation:
Number of beads they get in all (b) = (Number of sections one box was divided × Number of beads in each section of one box) + (Number of sections other box was divided × Number of beads in each section of other box)
= (6 × 10) + (4 ×9)
= 60 + 49
= 109.

c. Solve the problem. Show all your work including numbers, words, or labeled sketches.
Answer:
Number of beads they get in all (b) = 109.

Explanation:
Number of boxes of beads to make some necklaces Jasmine and her mother bought = 2.
Number of sections one box was divided = 6.
Number of beads in each section of one box = 10.
Number of sections other box was divided = 4.
Number of beads in each section of other box = 9.
Number of beads they get in all (b) = (Number of sections one box was divided × Number of beads in each section of one box) + (Number of sections other box was divided × Number of beads in each section of other box)
= (6 × 10) + (4 ×9)
= 60 + 49
= 109.

d. Does your answer make sense? How do you know?
Answer:
Yes, my answer makes sense because its the solution way to solve the problem asked.

Explanation:
Number of boxes of beads to make some necklaces Jasmine and her mother bought = 2.
Number of sections one box was divided = 6.
Number of beads in each section of one box = 10.
Number of sections other box was divided = 4.
Number of beads in each section of other box = 9.
Number of beads they get in all (b) = (Number of sections one box was divided × Number of beads in each section of one box) + (Number of sections other box was divided × Number of beads in each section of other box)
= (6 × 10) + (4 ×9)
= 60 + 49
= 109.

Question 4.
CHALLENGE Write a two-step story problem to match this equation: (4 × 25) – 28. Then solve your own problem.
Answer:
Question: Tom bought a sheet of stickers with 4 rows of 25 stickers on it. He gave 28 of the stickers to his little sister. How many stickers did he have left?
Solution: Number of stickers he have left (m) = (Number of stickers of rows Tom bought a sheet × Number of stickers on it) – Number of stickers he gave to his little sister
= (4 × 25) – 28
= 72.

Explanation:
Given Equation:
(4 × 25) – 28.
Question: Tom bought a sheet of stickers with 4 rows of 25 stickers on it. He gave 28 of the stickers to his little sister. How many stickers did he have left?
Solution: Number of stickers of rows Tom bought a sheet = 4.
Number of stickers on it = 25.
Number of stickers he gave to his little sister = 28.
Number of stickers he have left (m) = (Number of stickers of rows Tom bought a sheet × Number of stickers on it) – Number of stickers he gave to his little sister
= (4 × 25) – 28
= 100 – 28
= 72.

Family Math Night

Question 1.
Flora is helping Mr. Jackson get ready for Family Math Night. Eight families are coming. Flora needs to count out 4 square pattern blocks and 3 triangle pattern blocks for each family. How many pattern blocks will she count out in all?
a. What is this problem asking you to figure out? Underline any information that can help you solve the problem.
Answer:
This problem is asking you to figure out how many total pattern blocks she counts out in all.

Explanation:
Number of families are coming = 8.
Number of square pattern blocks Flora needs to count out for each family = 4.
Number of triangle pattern blocks Flora needs to count out for each family = 3.
Total number of pattern blocks she counts out in all = Number of families are coming × (Number of square pattern blocks Flora needs to count out for each family + Number of triangle pattern blocks Flora needs to count out for each family )
= 8 × (4 + 3)
= 8 × 7
= 56.

b. Choose the equation that best represents this problem. (The letter p stands for pattern blocks.)
4 + 3 + 8 = p
(4 + 3) × 8 = p
4 × 3 × 8 = p
(4 × 3) – 8 = p
Answer:
Equation that best represents this problem:
(4 + 3) × 8 = p.

Explanation:
Total number of pattern blocks she counts out in all = Number of families are coming × (Number of square pattern blocks Flora needs to count out for each family + Number of triangle pattern blocks Flora needs to count out for each family )
= 8 × (4 + 3)
= 8 × 7
= 56.

c. Solve the problem. Show your work.
Answer:
Total number of pattern blocks she counts out in all = 56.

Question 2.
Jared is also helping Mr. Jackson get ready for Family Math Night. Jared needs to count out 5 red game markers and 5 blue game markers for each of the 8 families. How many game markers will he count out in all?
a. Write an equation to represent the problem. Use a letter to stand for the unknown number.
Answer:
Number of game markers he counts out in all (m) = (Number of red game markers Jared needs to count out + Number of blue game markers Jared needs to count out) × Number of families
= (5 + 5) × 8
= 10 × 8
= 80.

Explanation:
Number of red game markers Jared needs to count out = 5.
Number of blue game markers Jared needs to count out = 5.
Number of families = 8.
Number of game markers he counts out in all (m) = (Number of red game markers Jared needs to count out + Number of blue game markers Jared needs to count out) × Number of families
= (5 + 5) × 8
= 10 × 8
= 80.

b. Solve the problem. Show your work.
Answer:
Number of game markers he counts out in all (m) = 80.

c. Is your answer reasonable? Why or why not?
Answer:
Yes, my answer is reasonable because it is accurate and process is correct.

Explanation:
Number of game markers he counts out in all (m) = (Number of red game markers Jared needs to count out + Number of blue game markers Jared needs to count out) × Number of families
= (5 + 5) × 8
= 10 × 8
= 80.

Bridges in Mathematics Grade 3 Student Book Unit 7 Module 1 Session 3 Answer Key

Multiplying by Eleven

Question 1.
Solve the problems below. Use your base ten area pieces to help if you want.
3 × 11 = _______________
11 × 5 = _______________
7 × 11 = _______________

Answer:
3 × 11 = 33.
11 × 5 = 55.
7 × 11 = 77.

Explanation:
Given equations:
3 × 11 = ??
=> 3 × 11 = 33.
11 × 5 = ??
=> 11 × 5 = 55.
7 × 11 = ??
=> 7 × 11 = 77.
4 × 11 = 44.
6 × 11 = 66.
10 × 11 = 110.
11 × 8 = 88.
11 × 9 = 99.
2 × 11 = 22.

Question 2.
Zack used his base ten area pieces to build this picture of 3 × 11. Jon used his base ten area pieces to build it a different way.

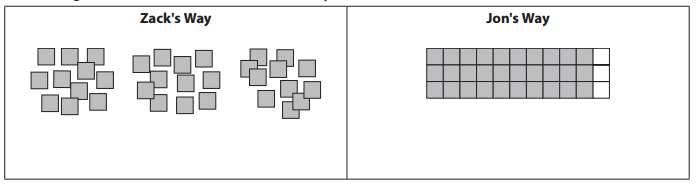
a. Write an equation below the picture in each box to show the total number of units.
Answer:

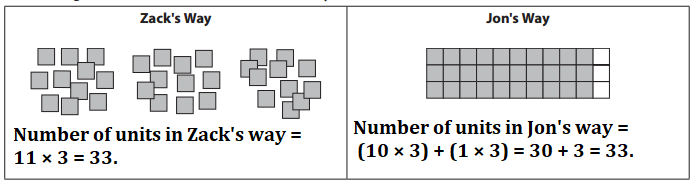
Explanation:
Number of units in Zack’s way = 11 × 3 = 33.
Number of units shaded = 10.
Number of units unshaded = 1.
Number of rows = 3.
Number of units in Jon’s way = (Number of units shaded × Number of rows) + (Number of units unshaded × Number of rows)
= (10 × 3) + (1 × 3)
= 30 + 3
= 33.

b. Which way do you like better? Why?
Answer:
Jon’s way is easy because it is simply and easy to get accurate answer.

Explanation:
Number of units in Zack’s way = 11 × 3 = 33.
Number of units in Jon’s way = (Number of units shaded × Number of rows) + (Number of units unshaded × Number of rows)
= (10 × 3) + (1 × 3)
= 30 + 3
= 33.

Question 3.
Jenna is starting a sticker book. There are 5 rows of stickers on each page, and each row has 11 stickers. So far, she’s filled 2 pages. How many stickers is that in all?
a. Write an equation for this problem. Use a letter to stand for the unknown quantity.
Answer:
Number of stickers are in all (s) = (Number of rows of stickers on each page × Number of stickers on each row has) × Number of pages she filled
= (5 × 11) × 2
= 110.

Explanation:
Number of rows of stickers on each page = 5.
Number of stickers on each row has = 11.
Number of pages she filled = 2.
Number of stickers are in all (s) = (Number of rows of stickers on each page × Number of stickers on each row has) × Number of pages she filled
= (5 × 11) × 2
= 55 × 2
= 110.

b. Solve the problem. Show all your work including numbers, words, or labeled sketches.
Answer:
Number of stickers are in all (s) = 110.

Multiplication, Division & Perimeter Practice

Question 1.
Complete the multiplication facts.

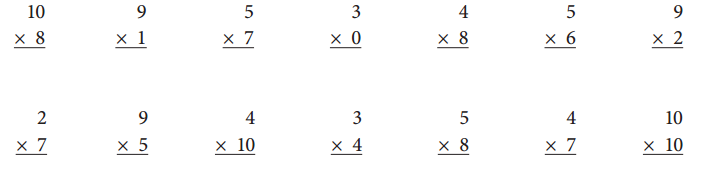
Answer:

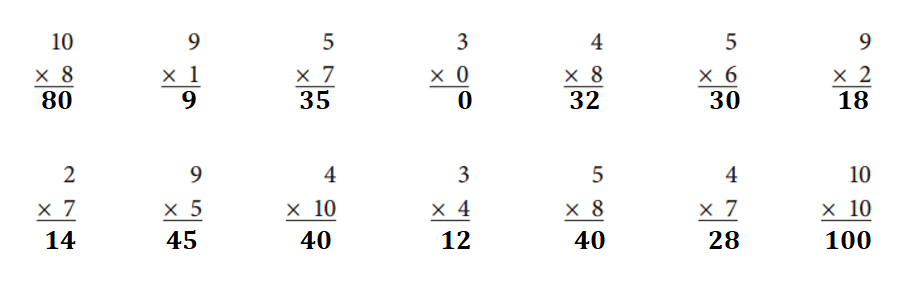
Explanation:
Given Equations:
Missing numbers:
10 × 8 = 80.
9 × 1 = 9.
5 × 7 = 35.
3 × 0 = 0.
4 × 8 = 32.
5 × 6 = 30.
9 × 2 = 18.
2 × 7 = 14.
9 × 5 = 45.
4 × 10 = 40.
3 × 4 = 12.
5 × 8 = 40.
4 × 7 = 28.
10 × 10 = 100.

Question 2.
Complete the division facts.
40 ÷ 5 = ______________
12 ÷ 2 = ______________
90 ÷ 10 = _____________
8 ÷ 1 = _____________
25 ÷ 5 = ______________
14 ÷ 2 = ______________
Answer:
Division Facts Equations:
40 ÷ 5 = 8.
12 ÷ 2 = 6.
90 ÷ 10 = 9.
8 ÷ 1 = 8.
25 ÷ 5 = 5.
14 ÷ 2 = 7.

Explanation:
Given Division Facts Equations:
40 ÷ 5 = ??
=> 40 ÷ 5 = 8.
12 ÷ 2 = ??
=> 12 ÷ 2 = 6.
90 ÷ 10 = ??
=> 90 ÷ 10 = 9.
8 ÷ 1 = ??
=> 8 ÷ 1 = 8.
25 ÷ 5 = ??
=> 25 ÷ 5 = 5.
14 ÷ 2 = ??
=> 14 ÷ 2 = 7.

Question 3.
Find the perimeter of each rectangle.
a. Perimeter = ____________

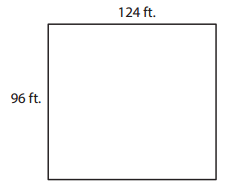
Answer:
Area of the rectangle = 11,904 square feet.

Explanation:
Length of the rectangle = 124 feet.
Breadth of the rectangle = 96 feet.
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
= 124 × 96
= 11,904 square feet.

b. Perimeter = ______________

Answer:
Area of the rectangle = 3,276 square feet.

Explanation:
Length of the rectangle = 117 feet.
Breadth of the rectangle = 28 feet.
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
= 117 × 28
= 3,276 square feet.

Question 4.
What is the difference between the perimeters of the rectangles above?
Answer:
8,628 square feet is the difference between the perimeters of the rectangles above.

Explanation:
a. Area of the rectangle = 11,904 square feet.
b. Area of the rectangle = 3,276 square feet.
Difference:
Area of the rectangle – Area of the rectangle
= 11,904 – 3,276
= 8,628 square feet.

Bridges in Mathematics Grade 3 Student Book Unit 7 Module 1 Session 4 Answer Key

Multiplying by Twelve

Question 1.
Solve the problems below. Use your base ten area pieces to help if you’d like.
4 × 12 = _____________
12 × 2 = _____________
5 × 12 = _____________

Answer:
Equations:
4 × 12 = 48.
12 × 2 = 48.
5 × 12 = 60.

Explanation:
Given Equations:
4 × 12 = ??
=> 4 × 12 = 48.
12 × 2 = ??
=> 12 × 2 = 48.
5 × 12 = ??
=> 5 × 12 = 60.
3 × 12 = 36.
6 × 12 = 72.
8 × 12 = 96.
12 × 7 = 84.

Question 2.
For each problem below:

Write an equation. Use a letter to stand for the unknown number.
Solve the problem. Show all your work including numbers, words, or labeled sketches.

a. Mrs. Green bought granola bars for the third grade field trip. There were 12 bars in a box. She bought 6 boxes and then found 4 more bars in her cupboard at school. How many bars did she have in all?

Answer:
Total number of bars she have in all = 76.

Explanation:
Number of bars in a box = 12.
Number of boxes she bought = 6.
Number of bars more she found in her cupboard at school = 4.
Total number of bars she have in all = (Number of bars in a box × Number of boxes she bought) + Number of bars more she found in her cupboard at school
= (12 × 6) + 4
= 72 + 4
= 76.

b. Mr. Lee got 8 dozen pencils from the office. So far, he’s given each of his third graders 3 pencils. He has 27 students. How many pencils does he still have left?

Answer:
Number of pencils he he has left = 15.

Explanation:
Number of dozen pencils from the office Mr. Lee got = 8.
Number of pencils he’s given each of his third graders = 3.
Number of students he has = 27.
Total number of pencils from the office Mr. Lee got = 12 × 8 = 96.
Number of pencils he gave to students = Number of pencils he’s given each of his third graders × Number of students he has
= 3 × 27
= 81.
Number of pencils he he has left = Total number of pencils from the office Mr. Lee got – Number of pencils he gave to students
= 96 – 81
= 15.

Meet the Elevens & Twelves Families

Write 2 multiplication and 2 division facts for each family. The first one has been done for you.

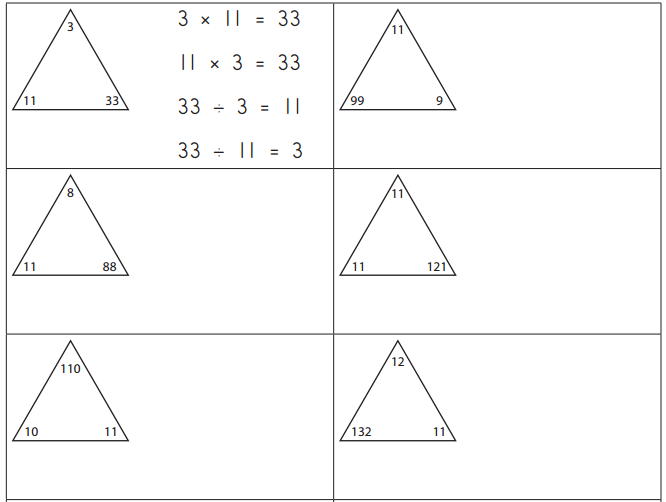
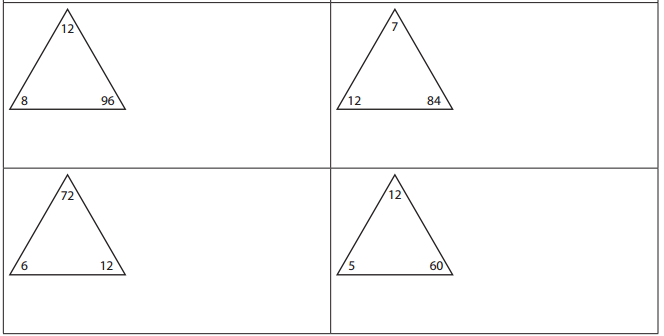
Answer:

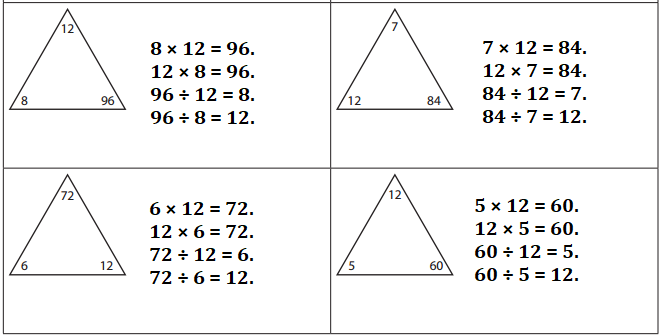
Explanation:
Given Numbers:
Multiplication and Division Equations of 11, 99, 9:
11 × 9 = 99.
9 × 11 = 99.
99 ÷ 9 = 11.
99 ÷ 11 = 9.
Multiplication and Division Equations of 11, 88, 8:
11 × 8 = 88.
8 × 11 = 88.
88 ÷ 8 = 11.
88 ÷ 11 = 8.
Multiplication and Division Equations of 11, 121, 11:
11 × 11 = 121.
121 ÷ 11 = 11.
Multiplication and Division Equations of 10, 110, 11:
11 × 10 = 110.
11 × 10 = 110.
110 ÷ 10 = 11.
110 ÷ 11 = 10.
Multiplication and Division Equations of 12, 132, 11:
11 × 12 = 132.
12 × 11 = 132.
132 ÷ 12 = 11.
132 ÷ 11 = 12.
Multiplication and Division Equations of 9, 96, 12:
8 × 12 = 96.
12 × 8 = 96.
96 ÷ 12 = 8.
96 ÷ 8 = 12.
Multiplication and Division Equations of 7, 84, 12:
7 × 12 = 84.
12 × 7 = 84.
84 ÷ 12 = 7.
84 ÷ 7 = 12.
Multiplication and Division Equations of 6, 72, 12:
6 × 12 = 72.
12 × 6 = 72.
72 ÷ 12 = 6.
72 ÷ 6 = 12.
Multiplication and Division Equations of 5, 60, 12:
5 × 12 = 60.
12 × 5 = 60.
60 ÷ 12 = 5.
60 ÷ 5 = 12.

Bridges in Mathematics Grade 3 Student Book Unit 7 Module 1 Session 5 Answer Key

Explore Six

Question 1.
Label the dimensions and area of the rectangle on each grid. Write a multiplication equation to match.
ex:

6 × 10 = 60

a.

Answer:

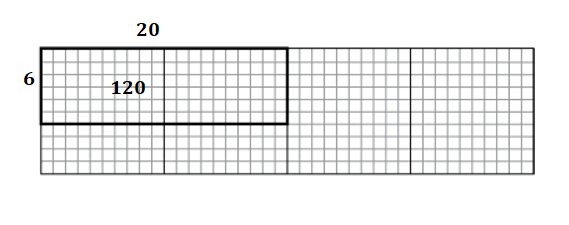
Explanation:
Length of the rectangle = 20 cubes.
Breadth of the rectangle = 6 cubes.
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
= 20 × 6
= 120 square cubes.

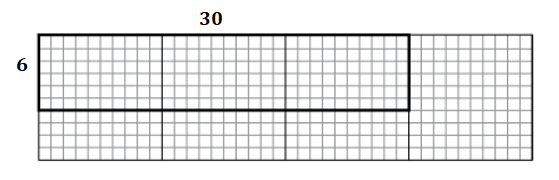
b.

Answer:

Explanation:
Length of the rectangle = 30 cubes.
Breadth of the rectangle = 6 cubes.
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
= 30 × 6
= 180 square cubes.

c.

Answer:

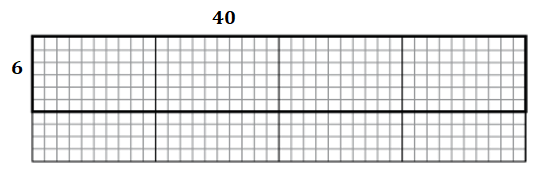
Explanation:
Length of the rectangle = 40 cubes.
Breadth of the rectangle = 6 cubes.
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
= 40 × 6
= 240 square cubes.

Question 2.
Use the information above to help solve these equations.
6 × 50 = _____________
6 × 60 = _____________
6 × 70 = _____________
6 × 80 = _____________
6 × 90 = _____________
6 × 100 = _____________
Answer:
6 × 50 = 300.
6 × 60 = 360.
6 × 70 = 420.
6 × 80 = 480.
6 × 90 = 540.
6 × 100 = 600.

Explanation:
Given Equations:
6 × 50 = ??
=> 6 × 50 = 300.
6 × 60 = ??
=> 6 × 60 = 360.
6 × 70 = ??
=> 6 × 70 = 420.
6 × 80 = ??
=> 6 × 80 = 480.
6 × 90 = ??
=> 6 × 90 = 540.
6 × 100 = ??
=> 6 × 100 = 600.

Explore More

Question 1.
Choose a number between 4 and 9 (not 6) to multiply by 10 and multiples of 10. Draw the missing dimensions and the area of each rectangle. Write a multiplication equation to match.
ex:

a.

Answer:

Explanation:
Length of the rectangle = 20 cubes.
Breadth of the rectangle = 9 cubes.
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
= 20 × 9
= 180 square cubes.

b.

Answer:

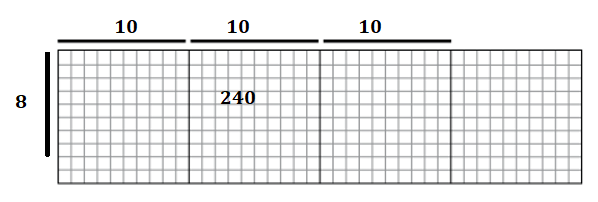
Explanation:
Length of the rectangle = 30 cubes.
Breadth of the rectangle = 8 cubes.
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
= 30 × 8
= 240 square cubes.

c.

Answer:

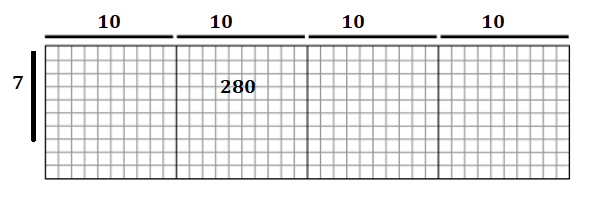
Explanation:
Length of the rectangle = 40 cubes.
Breadth of the rectangle = 7 cubes.
Area of the rectangle = Length of the rectangle × Breadth of the rectangle
= 40 × 7
= 280 square cubes.

Question 2.
Complete these equations using the number you chose.
___________ × 50 = ___________
___________ × 60 = ___________
___________ × 70 = ___________
___________ × 80 = ___________
___________ × 90 = ___________
___________ × 100 = ___________
Answer:
Equations:
4 × 50 = 200.
5 × 60 = 300.
6 × 70 = 420.
7 × 80 = 560.
8 × 90 = 720.
9 × 100 = 900.

Explanation:
Given Equations to fill:
?? × 50 = ??.
=> 4 × 50 = 200.
?? × 60 = ??.
=> 5 × 60 = 300.
?? × 70 = ??.
=> 6 × 70 = 420.
?? × 80 = ??.
=> 7 × 80 = 560.
?? × 90 = ??.
=> 8 × 90 = 720.
?? × 100 = ??.
=> 9 × 100 = 900.

Multiplying by Multiples of Ten

Question 1.
Solve these problems in your head. Write the answers.

Answer:
Missing products for the given equations:

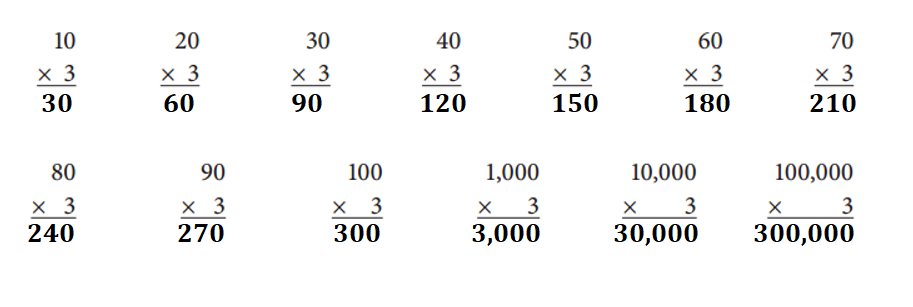
Explanation:
Given Equations:
10 × 3 = 30.
20 × 3 = 60.
30 × 3 = 90.
40 × 3 = 120.
50 × 3 = 150.
60 × 3 = 180.
70 × 3 = 210.
80 × 3 = 240.
90 × 3 = 270.
100 × 3 = 300.
1,000 × 3 = 3,000.
10, 000 × 3 = 30,000.
100,000 × 3 = 300,000.

Question 2.
Jon says the problems above are easy. Do you agree with him? Why or why not?
Answer:
Yes, I agree with Jon. Jon says the problems above are easy because multiplication is done to find the product of number mulitplied with 10, 100, 1000, 10000, 100000.

Explanation:
Given above equations are easy to calculate because multiplication is done to find the product of number mulitplied with 10, 100, 1000, 10000, 100000.

Question 3.
Solve these problems in your head. Write the answers.

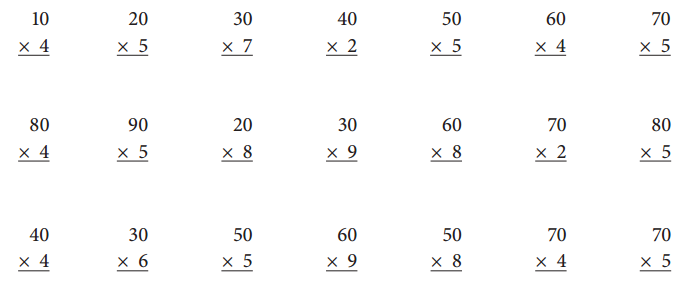
Answer:
Equation Missing products to find:

Explanation:
Given Equations:
10 × 4 = 40.
20 × 5 = 100.
30 × 7 = 210.
40 × 2 = 80.
50 × 5 = 250.
60 × 4 = 240.
70 × 5 = 350.
80 × 4 = 320.
90 × 5 = 450.
20 × 8 = 160.
30 × 9 = 270.
60 × 8 = 480.
70 × 2 = 140.
80 × 5 = 400.
40 × 4 = 160.
30 × 6 = 180.
50 × 5 = 250.
60 × 9 = 540.
50 × 8 = 400.
70 × 4 = 280.
70 × 5 = 350.

CHALLENGE

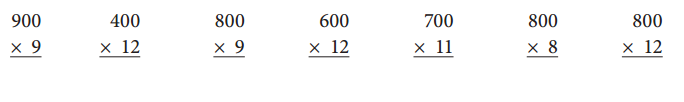
Answer:

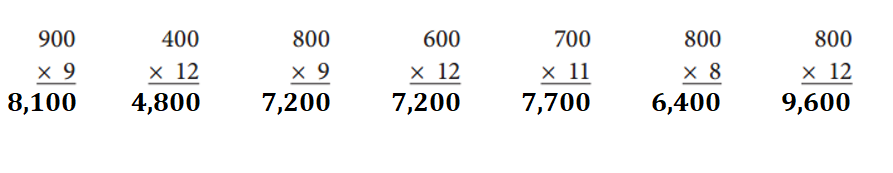
Explanation:
Given Equations missing products:
900 × 9 = ??
=> 900 × 9 = 8,100.
400 × 12 = ??
=> 400 × 12 = 4,800.
800 × 9 = ??
=> 800 × 9 = 7,200.
600 × 12 = ??
=> 600 × 12 = 7,200.
700 × 11 = ??
=> 700 × 11 = 7,700.
800 × 8 = ??
=> 800 × 8 = 6,400.
800 × 12 = ??
=> 800 × 12 = 9,600.

Bridges in Mathematics Grade 3 Student Book Answer Key Unit 7 Module 1

Leave a Comment Cancel Reply