Big Ideas Math Answer Key for Grade 7 Chapter 9 Geometric Shapes and Angles meets the content and intent of the School Curriculum. By using the Big Ideas Math Answers Grade 7 Chapter 9 Geometric Shapes and Angles, you can understand the topics easily. So, the students who wish to improve their math skills can go through our BIM Grade 7 Chapter 9 Geometric Shapes and Angles Answer Key pdf.
Big Ideas Math Book 7th Grade Answer Key 9 Geometric Shapes and Angles
People of highly subject expertise prepared the solutions in a concise manner for easy grasping. Ace up your preparation using the Big Ideas Math Book 7th Grade Answer Key 9 Geometric Shapes and Angles. By using the Big Ideas Math Answers Grade 7 Chapter 9 Geometric Shapes and Angles, you can understand the concepts in depth and score the highest marks in the exam.
Performance Task
- Geometric Shapes and Angles STEAM Video/Performance Task
- Geometric Shapes and Angles Getting Ready for Chapter 9
Lesson: 1 Circles and Circumference
Lesson: 2 Areas of Circles
Lesson: 3 Perimeters and Areas of Composite Figures
- Lesson 9.3 Perimeters and Areas of Composite Figures
- Perimeters and Areas of Composite Figures Homework & Practice 9.3
Lesson: 4 Constructing Polygons
Lesson: 5 Finding Unknown Angle Measures
Chapter 9 – Geometric Shapes and Angles
- Geometric Shapes and Angles Connecting Concepts
- Geometric Shapes and Angles Chapter Review
- Geometric Shapes and Angles Practice Test
- Geometric Shapes and Angles Cumulative Practice
Geometric Shapes and Angles STEAM Video/Performance Task
STEAM Video
Track and Field
Different lanes on a race track have different lengths. How can competitors run in different lanes and have the same finish line?
Watch the STEAM Video “Track and Field.” Then answer the following questions.
1. A track consists of a rectangle and two semicircles. The dimensions of the rectangle formed by the innermost lane are shown. What is the distance around each semicircle on the 400-meter, innermost lane?

2. How does the width of the rectangle, 63.7 meters, compare to the distance around each semicircle? Explain.
Answer:
1. The distance around each semicircle on the 400-meter, innermost lane = 488 m
2. The distance around each semicircle = 90π + 320
Explanation:
1. The inside perimeter of the track = 400 m
the total length of the two straight portions = 90 + 90 = 180
therefore the length of the remaining portion = 400-180 = 220 m
circumference of the two remaining semi-circular portions = πr + πr = 2πr
2πr = 220
2 x 3.14 x r = 220
r = 35 m
Area of the track = 2 x 90 x 14 +3.14 x (49) x (49) – (35) x (35)
area of the track = 6216 square meter
length of the outer running track = 488 m
2. The perimeter of the track is the two circumferences of the circumferences.
The diameters of the circle and the width of the rectangle = 90 m
90 π + 320
Performance Task.
Finding the Area and Perimeter of a Track
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given the dimensions of a race track.
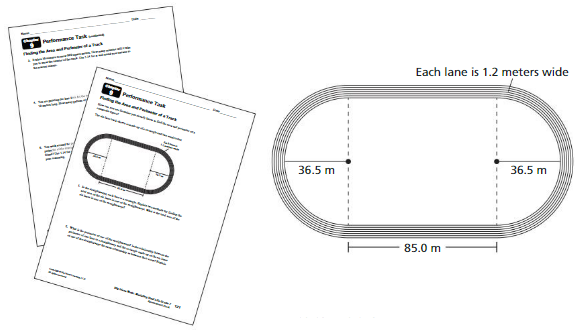
You will be asked to solve various perimeter and area problems about the track. Given a race track, what measures do you need to find the outer perimeter?
Answer:
The outer perimeter = 11,2610 sq m
Explanation:
perimeter of the semicircle = (π + 2 ) r
p = (3.14 + 2)36.5
p= (3.16) 36.5
p = 11,2610 sq m
Geometric Shapes and Angles Getting Ready for Chapter 9
Chapter Exploration
Work with a partner.
Question 1.
Perform the steps for each of the figures.
- Measure the perimeter of the larger polygon to the nearest millimeter.
- Measure the diameter of the circle to the nearest millimeter.
- Measure the perimeter of the smaller polygon to the nearest millimeter.
- Calculate the value of the ratio of the two perimeters to the diameter.
- Take the average of the ratios. This average is the approximation of π(the Greek letter ).
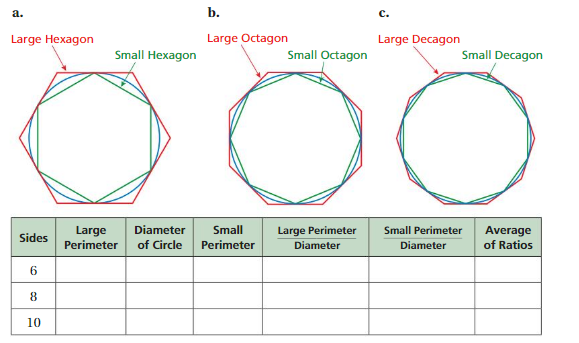
Question 2.
Based on the table, what can you conclude about the value of π? Explain your reasoning.
Answer:
The value of π = 3.14
Explanation:
We can consider 3 values for the π.
they are (22/7) or 3.14
so i am considering the 3.14
Question 3.
The Greek mathematician Archimedes used the above procedure to approximate the value of π. He used polygons with 96 sides. Do you think his approximation was more or less accurate than yours? Explain your reasoning.
Answer:
The greek mathematician used polygons with the side of polygons as 12,14,48, and finally 96 sides.
Explanation:
The greek mathematician used polygons with the side of polygons as 12,14,48, and finally 96 sides.
yes the accuration is more than i think.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
diameter of a circle
semi circle
adjacent angles
circumference
composite figure
vertical angles
Answer:
The diameter of the circle = the diameter is the length of the line through the center that touches two points on the edge of the circle.
semi circle = semicircle is a one-dimensional locus of points that forms half of the circle.
adjacent angles = adjacent angles are two angles that have a common vertex and a common side but do not overlap.
circumference = the circumference is the perimeter of the circle. the circumference would be the arc length of the circle.
composite figure = a figure that consists of two or more geometric shapes.
vertical angles = a pair of non-adjacent angles form when two lines intersect.
Explanation:
The diameter of the circle = the diameter is the length of the line through the center that touches two points on the edge of the circle.
semi circle = semicircle is a one-dimensional locus of points that forms half of the circle.
adjacent angles = adjacent angles are two angles that have a common vertex and a common side but do not overlap.
circumference = the circumference is the perimeter of the circle. the circumference would be the arc length of the circle.
composite figure = a figure that consists of two or more geometric shapes.
vertical angles = a pair of non-adjacent angles form when two lines intersect.
Lesson 9.1 Circles and Circumference
EXPLORATION 1
Using a Compass to Draw a Circle
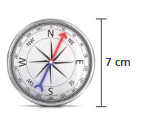
Work with a partner. Set a compass to 2 inches and draw a circle.

a. Draw a line from one side of the circle to the other that passes through the center. What is the length of the line? This is called the diameter of the circle.
b. Estimate the distance around the circle. This is called the circumference of the circle. Explain how you found your answer.
Answer:
a. the length of the line = 4 inches
b. The circumference of the circle = 12.56 inch
Explanation:
a. In the question they said that 2 inches
the length of the line = 4 in
b. the circumference of the circle = 2π r
circle = 2 x 3.14 x 2
circle = 12.56 in
EXPLORATION 2
Exploring Diameter and Circumference
Work with a partner.
a. Roll a cylindrical object on a flat surface to find the circumference of the circular base.

b. Measure the diameter of the circular base. Which is greater, the diameter or the circumference? how many times greater?
c. Compare your answers in part(b) with the rest of the class. What do you notice?
d. Without measuring, how can you find the circumference of a circle with a given diameter? Use your method to estimate the circumference of the circle in Exploration 1.
Answer:
a. The circumference of the circle = 2πr
b. The circumference of the circle is 3.14 times greater than the diameter of the circle.
c. The circumference of the circle is greater than the diameter of the circle.
d. The diameter of the circle = 2r and the circumference of the circle = 2πr
Explanation:
a. The circumference of the circle = 2πr
b. The circumference of the circle is 3.14 times greater than the diameter of the circle.
c. The circumference of the circle is greater than the diameter of the circle.
d. The diameter of the circle = 2r and the circumference of the circle = 2πr

Try It
Question 1.
The diameter of a circle is 16 centimeters. Find the radius.
Answer:
radius = 8 cm
Explanation:
The diameter of the circle = 2r
16 = 2r
r = 8 cm
Question 2.
The radius of a circle is 9 yards. Find the diameter.
Answer:
The diameter = 18 yds
Explanation:
The diameter of the circle = 2r
diameter = 2 x 9
r = 18 yds
Find the circumference of the object. Use 3.14 or \(\frac{22}{7}\) for π.
Question 3.

Answer:
circumference = 12.56 cm
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 2 where r = 2cm given
circle = 6.28 x 2
circle = 12.56 cm
Question 4.
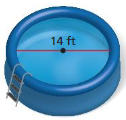
Answer:
circumference =43.96 square feet
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 7 where r = 7 ft given
circle = 6.28 x 7
circle = 43.96 square feet
Question 5.
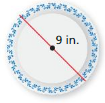
Answer:
circumference =28.26 square in
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 4.5 where r = 4.5 is given
circle = 6.28 x 4.5
circle =28.26 in
Find the perimeter of the semicircular region.
Question 6.
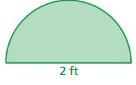
Answer:
perimeter of the semicircle = 5.14 ft
Explanation:
perimeter of the semicircle = (π + 2 ) r
perimeter = (3.14 + 2) 1 diameter = 2 given r= 1
perimeter = 5.14 feet
Question 7.
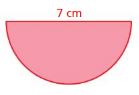
Answer:
perimeter of the semicircle = 17.99 cm
Explanation:
perimeter of the semicircle = (π + 2 ) r
perimeter = (3.14 + 2) 3.5 diameter = 7 given r= 3.5
perimeter = 17.99 cm
Question 8.
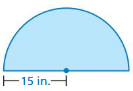
Answer:
the perimeter of the semicircle = 33.14 in
Explanation:
perimeter of the semicircle = (π + 2 ) r
perimeter = (3.14 + 2) 15 given r= 15
perimeter = 33.14 in
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
WRITING
Are there circles for which the value of the ratio of circumference to diameter is not equal to π? Explain.
Answer:
circumference to diameter is equal to π
Explanation:
d. The diameter of the circle = 2r and the circumference of the circle = 2πr
circumference to diameter is equal to π
Question 10.
FINDING A PERIMETER
Find the perimeter of a semicircular region with a straight side that is 8 yards long.
Answer:
perimeter = 11.14 yd
Explanation:
perimeter of the semicircle = (π + 2 ) r
perimeter = (3.14 + 2) 4 given r= 4
perimeter = 11.14 yd
Question 11.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
What is π times the radius?
What is π times the diameter?
Explanation:
the radius of the circle = (c/2 π )
the diameter of the circle = 2r
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
The wheels of a monster truck are 66 inches tall. Find the distance the monster truck travels when the tires make one 360-degree rotation.

Answer:
The distance = 207.35 inches
Explanation:
The wheel is in the shape of a circle.
diameter = 66 given
radius = (66/2)
radius = 33
The circumference = 2πr
c = 2 x 3.14 x 33
c = 6.28 x 33
c = 207.24 in
Question 13.
DIG DEEPER!
The radius of a dog’s collar should be at least 0.5 inch larger than the radius of the dog’s neck. A dog collar adjusts to a circumference of 10 to 14 inches. Should the collar be worn by a dog with a neck circumference of 12.5 inches? Explain.

Answer:
No, the collar should not be worn by this dog.
Explanation:
Given that the collar should be at least 0.5 inches.
dog collar adjusts to a circumference of 10 to 14 inches.
Question 14.
You resize a picture so that the radius of the midday Sun appears four times larger. How much larger does the circumference of the Sun appear? Explain.
Answer:
4 times larger
Explanation:
they said that if they resize it for 4 times.
therefore the sun appears 4 times larger.
Circles and Circumference Homework & Practice 9.1
Review & Refresh
Two jars each contain 1000 numbered tiles. The double box-and-whisker plot represents a random sample of 10 numbers from each jar.

Question 1.
Compare the samples using measures of center and variation.
Answer:
a. Jar A = median 3, starting 2.
b. Jar B = median 6, starting 2
Explanation:
In the above-given figure, the jar A is starting from 2
jar A contains median = 3
the jar B is starting from 2
jar B contains median = 6
Question 2.
Can you determine which jar contains greater numbers? Explain.
Answer:
Jar B
Explanation:
jar B contains the numbers from 4 to 9
Question 3.
Find the percent of change from 24 to 18.
A. 25% decrease
B. 25% increase
C. 75% increase
D. 75% decrease
Answer:
option A is correct
Explanation:
if the percent of jar changes from 24 to 18
the decrease in the percent = 25
Concepts, Skills, & Problem Solving
EXPLORING DIAMETER AND CIRCUMFERENCE Estimate the circumference of the circular base of the object. (See Exploration 2, p. 361.)
Question 4.
tube of lip balm with radius 0.5 mm
Answer:
c = 3.14 mm
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 0.5 where r = 0.5 mm given
circle = 6.28 x 0.5
circle =3.14 mm
Question 5.
D battery with radius 0.65 in.
Answer:
c = 4.082 in
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 0.65 where r = 0.65 ingiven
circle = 6.28 x 0.65
circle =4.082 in
FINDING A RADIUS Find the radius of the button.
Question 6.

Answer:
radius =2.5 cm
Explanation:
radius = (5/2)
radius = 2.5 cm
Question 7.

Answer:
radius =14 mm
Explanation:
radius = (28/2)
radius = 14 mm
Question 8.
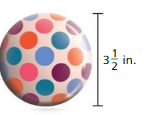
Answer:
radius =1.75 in
Explanation:
radius = (3.5/2)
radius = 1.75 in
FINDING A DIAMETER Find the diameter of the object.
Question 9.
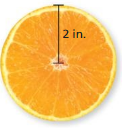
Answer:
diameter = 4 in
Explanation:
diameter of the circle = 2r
where r = 2 given
d = 4 in
Question 10.
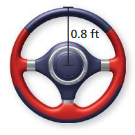
Answer:
diameter = 0.64 ft
Explanation:
diameter of the circle = 2r
where r = 0.8 given
d = 0.64 ft
Question 11.

Answer:
diameter = 1.2 cm
Explanation:
diameter of the circle = 2r
where r = 0.6 given
d = 1.2 cm
FINDING A CIRCUMFERENCE Find the circumference of the object. Use 3.14 or \(\frac{22}{7}\) for π.
Question 12.

Answer:
c = 43.96 in
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 7 where r = 7 ingiven
circle = 6.28 x 7
circle =43.96 in
Question 13.

Answer:
c = 18.84 cm
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 7 where r = 3 cmgiven
circle = 6.28 x 3
circle =18.84 cm
Question 14.

Answer:
c = 6.28 mm
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 1where r = 1mgiven
circle = 6.28 x 1
circle =6.28 m
FINDING THE PERIMETER OF A SEMICIRCULAR REGION Find the perimeter of the window.
Question 15.
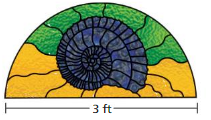
Answer:
perimeter = 7.71 ft
Explanation:
perimeter of the semicircle = (π + 2 ) r
perimeter = (3.14 + 2) 1.5 given d =3 ,r = (d/2)
perimeter = 7.71 ft
Question 16.
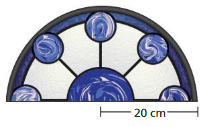
Answer:
perimeter = 64.8 cm
Explanation:
perimeter of the semicircle = (π + 2 ) r
perimeter = (3.14 + 2) 20 given ,r = 20 cm
perimeter = 64.8 cm
ESTIMATING A RADIUS Estimate the radius of the object.
Question 17.

Answer:
Radius = 1.417 mm
Explanation:
radius of the circle = (c/2π )
r = (8.9/6.28)
r = 1.417 mm
Question 18.

Answer:
Radius = 19.426 in
Explanation:
radius of the circle = (c/2π )
r = (122/6.28)
r = 19.426 in
Question 19.
MODELING REAL LIFE
A circular sinkhole has a circumference of 75.36 meters. A week later, it has a circumference of 150.42 meters.
a. Estimate the diameter of the sinkhole each week.
b. How many times greater is the diameter of the sinkhole a week later?
Answer:
a. The diameter of the sinkhole each week = 4 in
b. 2 times greater is the diameter of the sinkhole a week later
Explanation:
a. The diameter of the sinkhole each week = 75.36 m
b. 2 times greater is the diameter of the sinkhole a week later
75.36 x 75.36 = 150.42 m
Question 20.
REASONING
Consider the circles A, B, C, and D.
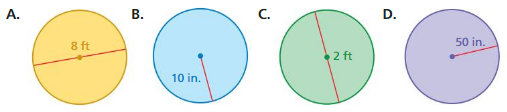
a. Without calculating, which circle has the greatest circumference? Explain.
b. Without calculating, which circle has the least circumference? Explain.
Answer:
a. option D has the greatest circumference.
b. option C has the least circumference.
Explanation:
D. circumference of the circle =2πr
circle = 2 x 3.14 x 50where r =50 ingiven
circle = 6.28 x 50
circle =314 in
Explanation:
C. circumference of the circle =2πr
circle = 2 x 3.14 x 1where r = 1given
circle = 6.28 x1
circle = 6.28
Explanation:
A. circumference of the circle =2πr
circle = 2 x 3.14 x 4 where r = 4given
circle = 6.28 x 4
circle = 25.12
Explanation:
A. circumference of the circle =2πr
circle = 2 x 3.14 x 10 where r = 10given
circle = 6.28 x 10
circle = 62.8
FINDING CIRCUMFERENCES Find the circumferences of both circles.
Question 21.
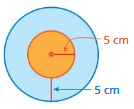
Answer:
circumference of inside circle =31.4 square cm
circumference of outside circle = 62.8 square cm
Explanation:
circumference of the inside circle =2πr
circle = 2 x 3.14 x 5 where r = 5 cm given
circle = 6.28 x 5
circle = 31.4 square cm
circumference of the outside circle =2πr
circle = 2 x 3.14 x 2 where r = 2 cm given
circle = 6.28 x 2
circle = 62.8 square cm
Question 22.
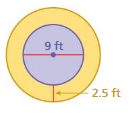
Answer:
circumference of inside circle =28.26 ft
circumference of outside circle = 31.4 square cm
Explanation:
circumference of the inside circle =2πr
circle = 2 x 3.14 x 4.5 where r = 4.5 feet given
circle = 6.28 x 4.5
circle = 28.26 ft
circumference of the outsideside circle =2πr
circle = 2 x 3.14 x 2.5 where r = 2.5 ft given
circle = 6.28 x 2.5
circle = 15.7 square ft
Question 23.
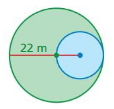
Answer:
circumference of inside circle =69.08 m
circumference of outside circle = 138.16 m
Explanation:
circumference of the inside circle =2πr
circle = 2 x 3.14 x 5.5 where r = 5.5 feet given
circle = 6.28 x 5.5
circle = 69.08 m
circumference of the outsideside circle =2πr
circle = 2 x 3.14 x 22 where r = 22given
circle = 6.28 x 22
circle = 138.16 m
Question 24.
MODELING REAL LIFE
A satellite is in an approximately circular orbit 36,000 kilometers from Earth’s surface. The radius of Earth is about 6400 kilometers. What is the circumference of the satellite’s orbit?

Answer:
c = 40,192 km
Explanation:
circumference of the satellite orbit =2πr
circle = 2 x 3.14 x 6400where r = 6400kmgiven
circle = 6.28 x 6400
circle =40,192km
Question 25.
STRUCTURE
The ratio of circumference to diameter is the same for every circle. Is the ratio of circumference to radius the same for every circle? Explain.
Answer:
The ratio of circumference to radius is same for every circle.
Explanation:
c/r = 2πr/r
where r get canceled in both numerator and denominator.
c/r = 2π
radius = (c/2π)
the radius is same for every circle.
Question 26.
PROBLEM SOLVING
A wire is bent to form four semicircles. How long is the wire? Justify your answer.
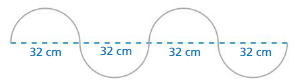
Answer:
The wire is 128 cm long
Explanation:
Given that the four semicircles are 32 cm
32 + 32 + 32 + 32 = 64
Question 27.
CRITICAL THINKING
Explain how to draw a circle with a circumference of π2 inches. Then draw the circle.
Answer:
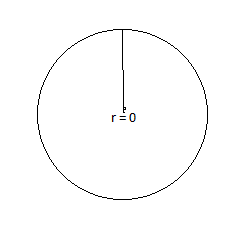
Explanation:
circumference of circle = 2πr
c = π2
Question 28.
DIG DEEPER!
“Lines” of latitude on Earth are actually circles. The Tropic of Cancer is the northernmost line of latitude at which the Sun appears directly overhead at noon. The Tropic of Cancer has a radius of 5854 kilometers.
To qualify for an around-the-world speed record, a pilot must cover a distance no less than the circumference of the Tropic of Cancer, cross all meridians, and land on the same air field where the flight began.
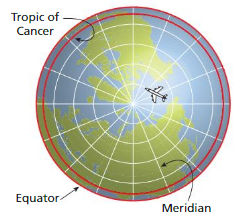
a. What is the minimum distance that a pilot must fly to qualify for an around-the-world speed record?
b. RESEARCH Estimate the time it will take for a pilot to qualify for the speed record. Explain your reasoning.
Answer:
a. The minimum distance that a pilot must fly to qualify for an around the world-speed record = 18.3376 km
b. The pilot will take for the speed record = 18.3376 km
Explanation:
a. The minimum distance that a pilot must fly to qualify for an around the world-speed record = 18.3376 km
b. The pilot will take for the speed record = 18.3376 km
Question 29.
PROBLEM SOLVING
Bicycles in the late 1800s looked very different than they do today.
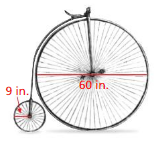
a. How many rotations does each tire make after traveling 600 feet? Round your answers to the nearest whole number.
b. Would you rather ride a bicycle made with two large wheels or two small wheels? Explain.
Answer:
a. The rotations each tire make after traveling 600 feet = 188.4 in in
b. two large wheels = 376.8 in
two small wheels = 113.04 in
Explanation:
the rotations each tire make after travelling = 2 x 3.14 x 30 = 188.4 in
b. two large wheels = 188.4 x 2 = 376.8 in
for two small wheels = 113.04 in
Question 30.
LOGIC
The length of the minute hand is 150% of the length of the hour hand.

a. What distance will the tip of the minute hand move in 45 minutes? Justify your answer.
b. In 1 hour, how much farther does the tip of the minute hand move than the tip of the hour hand? Explain how you found your answer.
Answer:
The distance will the tip of minute hand move in 45 minutes = 140 %
b. the tip of the minute hand moves 60 times faster than hour hand.
Explanation:
The distance will the tip of minute hand move in 45 minutes = 140 %
b. the tip of the minute hand moves 60 times faster than hour hand.
Lesson 9.2 Areas of Circles
EXPLORATION 1
Estimating the Area of a Circle
Work with a partner. Each grid contains a circle with a diameter of 4 centimeters. Use each grid to estimate the area of the circle. Which estimate should be closest to the actual area? Explain.
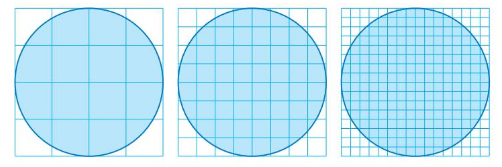
Answer:
Area of 1st circle = 200.96 cm
Area of 2nd circle =803.84 cm
Area of 3rd circle =3215.36 cm
Explanation:
area of 1st circle = πr x r
area = 3.14 x 8 x 8
a = 200.96 cm
area of 2nd circle = πr x r
area= 3.14 x 16 x 16
a = 803.84 cm
area of 3rd circle = πr x r
area= 3.14 x 32 x 32
a = 3215.36
EXPLORATION 2
Writing a Formula for the Area of a Circle
Work with a partner. A student draws a circle with radius and divides the circle into 24 equal sections. The student cuts out each section and arranges the sections to form a shape that resembles a parallelogram.
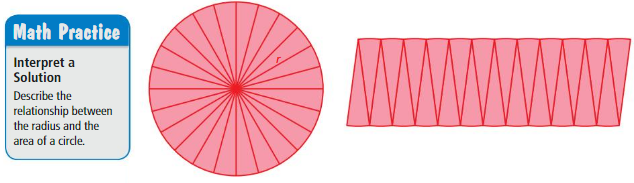
a. Use the diagram to write a formula for the area of a circle in terms of the radius r. Explain your reasoning.Describe the relationship between the radius and the area of a circle.
b. Use the formula to check your estimates in Exploration 1.
Answer:
a. the area of the circle = 1808.64
b. the area of the circle in terms of radius r = 0.0084 cm
Explanation:
The area of circle = πr x r
a = 3.14 x 24 x 24
a = 1808.64 cm
The radius of the circle = (c/2 π)
circumference = 2πr
c = 2 x 3.14 x 24
c = 150.72 cm
area = (150.72/6.28)
area = 0.0084 cm
Try It
Question 1.
Find the area of a circle with a radius of 6 feet. Use 3.14 for π.
Answer:
The area of circle = 113.04 sq ft
Explanation:
The area of circle = πr x r
a = 3.14 x 6 x 6
a = 113.04 square feet
Question 2.
Find the area of a circle with a diameter of 28 meters.Use \(\frac{22}{7}\) for π.
Answer:
The area of circle = 175.84 sq meters
Explanation:
The area of circle = πr x r
a = 3.14 x 14 x 14 where d = 28 so r = 14
a = 175.84 square meters
Find the area of the semicircle.
Question 3.
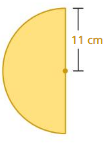
Answer:
Area of semicircle =62.07 sq cm
Explamation:
Area of semicircle =( π+r x r/2)
area =( 3.14 +121/2)
area =(121.14/2)
area = 62.07 sq cm
Question 4.
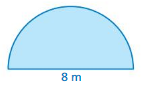
Answer:
Area of semicircle =9.57 sqm
Explamation:
Area of semicircle =( π+r x r/2)
area =( 3.14 +16/2)
area =(19.14/2)
area = 9.57 sq m
Question 5.
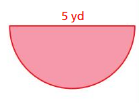
Answer:
Area of semicircle =4.695 sq yd
Explanation:
Area of semicircle =( π+r x r/2)
area =( 3.14 +6.25/2)
area =(9.39/2)
area = 4.695 sq yd
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 6.
ESTIMATING AN AREA
The grid contains a circle with a diameter of 2 centimeters. Use the grid to estimate the area of the circle. How can you change the grid to improve your estimate? Explain.

Answer:
The area of circle = 50.24 sq centi meters
Explanation:
The area of circle = πr x r
a = 3.14 x 4 x 4 where d = 8 so r = 4
a = 50.24 square centimeters
Question 7.
WRITING
Explain the relationship between the circumference and area of a circle.
Answer:
The area of circle = πr x r
circumference of circle = 2πr
Explanation:
The circumference of the circle is 2 times greater than the area of the circle.
The area of circle = πr x r
circumference of circle = 2πr
Question 8.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
What is area of a circle with a radius of 100 cm?
What is the area of a circle with a radius of 500 mm?
Explanation:
The area of circle = πr x r
area = 3.14 x 100 x 100
area = 31400 sq cm
The area of circle = πr x r
area = 3.14 x 500 x 500
area = 785000 sq mm
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
A local event planner wants to cover a circular region with mud for an obstacle course. The region has a circumference of about 157 feet. The cost to cover 1 square foot with mud is $1.50. Approximate the cost to cover the region with mud.

Answer:
Cost to cover =
Question 10.
DIG DEEPER!
A manufacturer recommends that you use a frying pan with a radius that is within 1 inch of the radius of your stove top burner. The area of the bottom of your frying pan is 25π square inches. The circumference of your cook top burner is 9π inches. Does your frying pan meet the manufacturer’s recommendation?
Answer:
no the frying pan does not meet the manufacture
Explanation:
Given that frying pan has radius = 1 inch
area of frying pan = 25π square inches
circumference = 9π inches
Areas of Circles Homework & Practice 9.2
Review & Refresh
Find the circumference of the object. Use 3.14 or \(\frac{22}{7}\) for π.
Question 1.

Answer:
c = 28.26cm
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 4.5where r = 4.5cmgiven
circle = 6.28 x 4.5
circle =28.26 cm
Question 2.
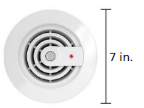
Answer:
c = 21.98 sq in
Explanation:
circumference of the circle =2πr
circle = 2 x 3.14 x 3.5where r = 3.5ingiven
circle = 6.28 x 3.5
circle =21.98 sq in
You spin the spinner shown.
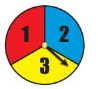
Question 3.
How many possible outcomes are there?
Answer:
3 possible outcomes
Explanation:
There are 3 possible outcomes.
3 numbers are there in the spin.
Question 4.
In how many ways can spinning an odd number occur?
Answer:
2 ways the spinning an odd number occur.
Explanation:
There are 2 possible ways that the odd numbers can occur.
Concepts, Skills, & Problem Solving
ESTIMATING AN AREA Use the grid to estimate the area of the circle. (See Exploration 1, p. 369.)
Question 5.
diameter of 3 centimeters
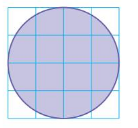
Answer:
area of the circle = 6.75 sq cm
Explanation:
The area of circle = πr x r
area = 3.14 x 1.5 x 1.5
area = 6.75 sq cm
Question 6.
diameter of 1.6 inches
Answer:
area of the circle = 141.41 sq in
Explanation:
The area of circle = πr x r
area = 3.14 x 6.4 x 6.4
area = 141.41 sq in
FINDING AN AREA Find the area of the circle. Use 3.14 or \(\frac{22}{7}\) for π.
Question 7.

Answer:
The area of circle = 254.34 sq milli meters
Explanation:
The area of circle = πr x r
a = 3.14 x 4 x 4 where d = 8 so r = 4
a = 254.34 square millimeters
Question 8.
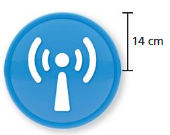
Answer:
The area of circle = 615.44 sq centi meters
Explanation:
The area of circle = πr x r
a = 3.14 x 14 x 14 where r = 14
a = 615.44 square centimeters
Question 9.

Answer:
The area of circle = 314 sq inches
Explanation:
The area of circle = πr x r
a = 3.14 x 10 x 10 where r = 10
a = 314 square inches
Question 10.
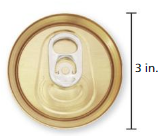
Answer:
The area of circle = 7.065 sq inches
Explanation:
The area of circle = πr x r
a = 3.14 x 1.5 x 1.5 where r = 1.5
a = 7.065 square inches
Question 11.

Answer:
The area of circle = 3.14 sq cm
Explanation:
The area of circle = πr x r
a = 3.14 x 1 x 1 where r = 1
a = 3.14 square cm
Question 12.

Answer:
area of circle = 1.76625sq ft
Explanation:
The area of circle = πr x r
a = 3.14 x 0.75 x 0.75 where r = 0.75
a = 1.76625 square ft
Question 13.
YOU BE THE TEACHER
Your friend finds the area of a circle with a diameter of 7 meters. Is your friend correct? Explain.

Answer:
No, my friend is not correct.
Explanation:
The area of circle = πr x r
a = 3.14 x 3.5 x 3.5 where r = 0.75
a = 38.465 square meters
Question 14.
MODELING REAL LIFE
The diameter of a flour tortilla is 12 inches. What is the total area of two tortillas?
Answer:
The area of tortilla = 226.08 sq inches
Explanation:
The area of tortilla = πr x r
a = 3.14 x 6 x 6 where r = 6
a = 113.04 square inches
for 2 tortilla = 226.08 sq inches
Question 15.
MODELING REAL LIFE
The diameter of a coaster is 7 centimeters. What is the total area of five coasters?
Answer:
The total area of coaster = 192.325 cm
Explanation:
The area of tortilla = πr x r
a = 3.14 x 3.5 x 3.5 where r = 3.5
a = 38.465 square cm
for 5 tortilla = 192.325 centimeters
Question 16.
PROBLEM SOLVING
The HillsboroInlet Lighthouse lights up how much more area than the Jupiter Inlet Lighthouse?
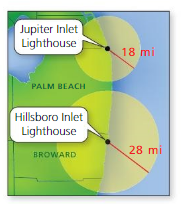
Answer:
The HillsboroInlet Lighthouse lights are 2 times greater than the Jupiter Inlet Lighthouse.
Explanation:
Hillsboro inlet Lighthouse = 3.14 x 28 x 28
area = 2,461.76 sq mi
jupiter inlet Lighthouse = 3.14 x 18 x 18
area = 1,017.36 sq mi
FINDING THE AREA OF A SEMICIRCLE Find the area of the semicircle.
Question 17.
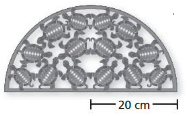
Answer:
Area of semicircle = 628 sq cm
Explanation:
Area of semicircle =( π+r x r/2)
area =( 3.14 +400/2)
area =(403.14/2)
area = 628 sq cm
Question 18.
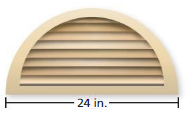
Answer:
Area of semicircle =201.57 sq cm
Explanation:
Area of semicircle =( π+r x r/2)
area =( 3.14 +400/2)
area =(403.14/2)
area = 201.57 sq cm
Question 19.
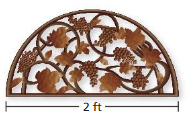
Answer:
Area of semicircle =1.57 sq ft
Explanation:
Area of semicircle =( π+r x r/2)
area =( 3.14 +1/2)
area =(3.14/2)
area = 1.57 sq ft
Question 20.
MODELING REAL LIFE
The plate for a microscope has a circumference of 100π millimeters. What is the area of the plate?
Answer:
Area of the plate = 200π mm
Explanation:
Area of the plate = π x r x r
area = 3.14 x 200 x 200
Question 21.
MODELING REAL LIFE
A dog is leashed to the corner of a house. How much running area does the dog have? Explain how you found your answer.
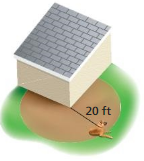
Answer:
Area of the circle = 942 sq ft
Explanation:
Area of the circle = π x r x r
area = 3.14 x 20 x 20
area = 942 sq ft
The running area is 3/4 the area of a circle with a radius of 20 feet.
Question 22.
REASONING
Target A has a circumference of 20 feet. Target B has a diameter of 3 feet. Both targets are the same distance away. Which target is easier to hit? Explain your reasoning.
Answer:
Target B is easier to hit
Explanation:
Target A =2 π x r
A = 2 x 3.14 x 3.18
A = 19.9704
Target B = 1.5
Question 23.
DIG DEEPER!
A circular oil spill has a radius of 2 miles. After a day, the radius of the oil spill increases by 3 miles. By how many square miles does the area of the oil spill increase?
Answer:
The area of oil spill increases by 65.94 miles.
Explanation:
Given that the circular oil spill has a radius of 2 miles.
The radius of the oil spill increases by 65.94 sq miles.
Question 24.
FINDING AN AREA
Find the area of the circle in square yards.

Answer:
Area of the circle = 7.057935 sq yd
Explanation:
Area of the circle = π x r x r
area = 3.14 x 4.5 x 4.5
area = 63.585 sq ft
area = 7.057935 sq yd
Question 25.
REPEATED REASONING
What happens to the circumference and the area of a circle when you double the radius? triple the radius? Justify your answer.
Answer:
If we double the radius ,area = π x r x r x r x r
If we double the radius, circumference = 2πr x r x r
If we triple the radius ,area = π x r x r x r x r x r
If we triple the radius, circumference = 2πr x r x r x r x r
Explanation:
circumference doubles and area quadruples;
circumference triples and area is 9 times greater;
double the radius: circumference = 2π2r = 4πr
4πr /2πr = 2 times larger, area =π (2r) x r =4πrx r
4πrx r/ πrx r = 4 times larger.
Question 26.
CRITICAL THINKING
Is the area of a semicircle with a diameter of x greater than, less than, or equal to the area of a circle with a diameter of \(\frac{1}{2}\)x? Explain.
Answer:
The area of a semicircle with a diameter of x is greater than the area of a circle with a diameter of (0.5)
Explanation:
Area of semicircle = (3.14 + (0.5 x 0.5)/2)
area = 1.695
Area of circle = (3.14 x 0.5 x 0.5)
area = 0.785
Lesson 9.3 Perimeters and Areas of Composite Figures
EXPLORATION 1
Submitting a Bid
Work with a partner. You want to bid on a project for the pool shown. The project involves ordering and installing the brown tile that borders the pool, and ordering a custom-made tarp to cover the surface of the pool. In the figure, each grid square represents 1 square foot. You pay $5 per linear foot for the tile.
- You pay $4 per square foot for the tarp.
- It takes you about 15 minutes to install each foot of tile.
a. Estimate the total cost for the tile and the tarp.
b. Write a bid for how much you will charge for the project.Include the hourly wage you will receive.Estimate your total profit.
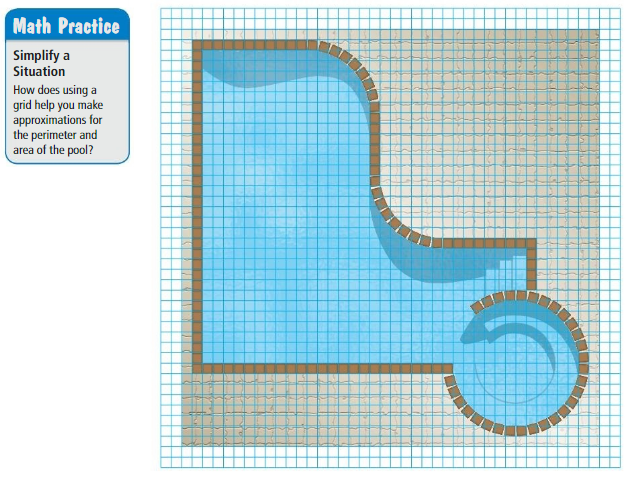
Answer:

Try It
Question 1.
Estimate the perimeter and the area of the figure.
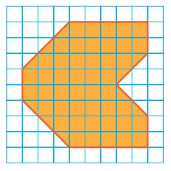
Answer:
50.24 sq mm
Explanation:
The above-given figure is about 50.24 sq mm
Question 2.
Find the perimeter and the area of the figure.
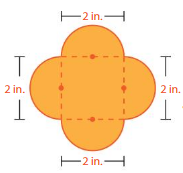
Answer:
perimeter of the figure = 3.16 sq in
area of the figure = 3.14 sq in
Explanation:
perimeter of the semicircle = ( π + 2) r
p = (3.14 + 2 ) 1
p = 3.16 in
area of the figure = π x r x r
area = 3.14 x 1 x1
area = 3.14 in
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 3.
ESTIMATING PERIMETER AND AREA
Estimate the perimeter and area of the figure at the right.
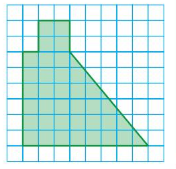
Answer:
The perimeter and area = 30 ft
area = π x r x r
Explanation:
The perimeter = ( π + 2) r
area = π x r x r
Question 4.
FINDING PERIMETER AND AREA
Identify the shapes that make up the figure at the left. Then find the perimeter and area of the figure.
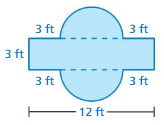
Answer:
The perimeter = 9.48 sq ft
area = 27.36 sq ft
Explanation:
The perimeter = ( π + 2) r
perimeter = 3.14 +2 x 3
perimeter = 9.48 sq ft
area = 3.14 x 3 x 3
area = 27.36 sq feet
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
A farmer wants to seed and fence a section of land. Fencing costs $27 per yard. Grass seed costs $2 per square foot. How much does it cost to fence and seed the pasture?
Answer:
1 m
Explanation:
Given that farmer has the fencing cost = $ 27
seed cost = $ 2
5.10 $ is used to cost for grass seed
$ 27 is used to fence = 1 m
Question 6.
DIG DEEPER!
In each room shown, you plan to put down carpet and add a wallpaper border around the ceiling. Which room needs more carpeting? more wallpaper?
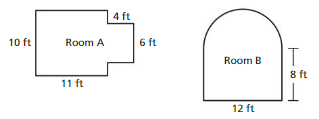
Answer:
Room A needs more carpeting.
Explanation:
Room A = 10 x 11
where length = 11 , breadth = 10 given
Room A = 110
Room B = 12 x 8
B = 96
Perimeters and Areas of Composite Figures Homework & Practice 9.3
Review & Refresh
Find the area of the circle. Use 3.14 or \(\frac{22}{7}\) for π.
Question 1.
Answer:
Area of the circle = 50.24 sq mm
Explanation:
Area of the circle = π x r x r
area = 3.14 x 4 x 4
area = 3.14 x 16
area = 50.24 sq mm
Question 2.
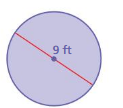
Answer:
Area of the circle = 63.585 sq ft
Explanation:
Area of the plate = π x r x r
area = 3.14 x 4.5 x 4.5
area = 3.14 x
area = 63.585 sq ft
Find the missing dimension. Use the scale 1 : 5.
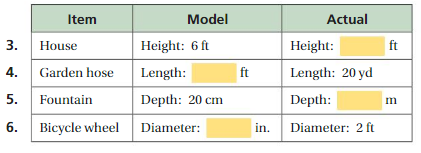
Answer:
3. Height = 30 ft
4. Length = 6 ft
5. Depth = 100 cm
6. Diameter = 2 in
Explanation:
3. house : height = 6 ft , height = 30 ft given that scale = 1 : 5
4. garden hose : length = 6 ft , length = 20 yd
4. fountain : depth = 20 cm, depth = 100 cm
5. bicycle wheel : = diameter = 2 in diameter = 2 ft
Concepts, Skills, & Problem Solving
ESTIMATING PERIMETER AND AREA You build a patio with a brick border. (See Exploration 1, p. 375.)
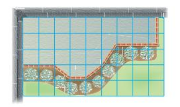
Question 7.
Estimate the perimeter of the patio.
Answer:
The perimeter of a patio = 24 units
Explanation:
In the above-given figure,
the perimeter of the patio = 24
Question 8.
Estimate the area of the patio.
Answer:
area of the patio = π r
ESTIMATING PERIMETER AND AREA Estimate the perimeter and the area of the shaded figure.
Question 9.
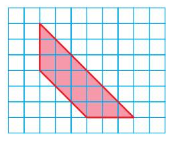
Answer:
Perimeter = 19.5 units
area =13.5 units
Explanation:
given figure is trapezoid
Perimeter = a + b + c + d
area =( (a + b) x h /2)
Question 10.
Answer:
area =( 3 √ 3/2) a square
perimeter = 6 a
Explanation:
given figure is hexagon
area =( 3 √ 3/2) a square
perimeter = 6 a
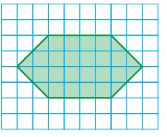
Question 11.
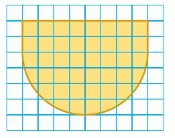
Answer:
The perimeter = 24.6 units
Area of the plate = 41.1 sq units
Explanation:
given figure is semicircle
The perimeter = ( π + 2) r
Area of the plate = π x r x r
Question 12.
Answer:
Perimeter = a + b + c + d
area =( (a + b) x h /2)
Explanation:
given figure is trapezoid
Perimeter = a + b + c + d
area =( (a + b) x h /2)
Question 13.
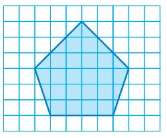
Answer:
Perimeter = 19 units
area = 24 squnits
Explanation:
given figure is pentagon
Perimeter = 5 a
area = ( perimeter x apotherm /2 )
Question 14.
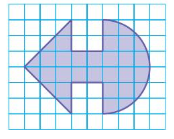
Answer:
Perimeter = a + b + c
area = ( height x breadth /2 )
Explanation:
given figure is triangle
Perimeter = a + b + c
area = ( height x breadth /2 )
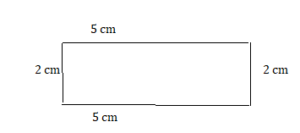
FINDING PERIMETER AND AREA Find the perimeter and the area of the figure.
Question 15.
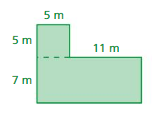
Answer:
area = 137 sq m
perimeter = 56 m
Explanation:
area of the rectangle = l x w
l = length, w = width
area = 12 x 11
area = 137 sq m
perimeter of the rectangle = 2 ( l + w)
perimeter = 2 (28)
perimeter = 56 m
Question 16.
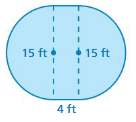
Answer:
area = 114.07 sq ft
perimeter = 47.4 sq ft
Explanation:
Area of semicircle =( π+r x r/2)
area =( 3.14 +225/2)
area =(228.14/2)
area = 114.07 sq ft
perimeter of the semicircle = (π + 2 ) r
perimeter = (3.14 + 2) 15 given r= 15
perimeter = 3.16 x 15
perimeter = 47.4 sq ft
Question 17.
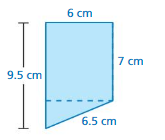
Answer:
area = 49.5 cm
perimeter = 29 cm
Explanation:
area of the rectangle = l x w
l = length, w = width
area = 7 x 7
area = 49 cm
perimeter of the rectangle = 2 ( l + w)
perimeter = 2 (14)
perimeter = 29 cm
Question 18.
YOU BE THE TEACHER
Your friend finds the perimeter of the figure. Is your friend correct? Explain your reasoning.

Answer:
Yes my friend is correct.
Explnation:
perimeter = length + side + height + breadth + width + base
p = 4 + 3 + 4 + 5 + 4 + 5
p = 25 in
Question 19.
LOGIC
A running track has six lanes. Explain why the starting points for the six runners are staggered. Draw a diagram as part of your explanation.

Answer:
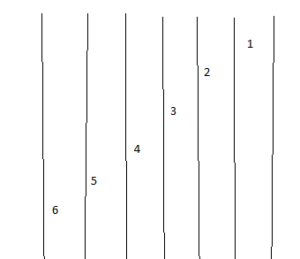
Explanation:
The starting points for the six runners are staggered because each runner can run the same distance.
Explanation:
The starting points are staggered so that each runner can run the same distance and use the same finish line.
this is necessary because the circumference is different for each lane.
the above-diagram shows this because the diameter is greater n the outer lanes.
Question 20.
PROBLEM SOLVING
You run around the perimeter of the baseball field at a rate of 9 feet per second. How long does it take you to run around the baseball field?
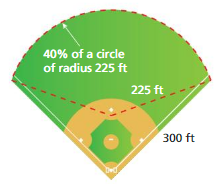
Answer:
It take to run around the baseball field = 1,58,962.5 sq feet
Explanation:
The area of the circle = π x r x r
area = 3.14 x 225 x 225
area = 1,58,962.5 sq feet
Question 21.
STRUCTURE
The figure at the right is made up of a square and a rectangle. Find the area of the shaded region.
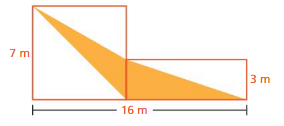
Answer:
The area of the shaded region =24 sq m
Ex planation:
Area of triangle = ( b x h )/2
area =( 8 x 7)/ 2
area = 48/2
area = 24 sq m
Question 22.
DIG DEEPER!
Your friend makes a two-dimensional model of a dividing cell as shown. The total area of the dividing cell is 350 square inches. What is the area of the shaded region?
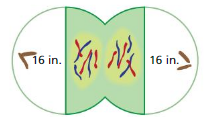
Answer:
The area of the shaded region = 1.89 sq in
Explanation :
area of semicircle = (π + r x r/2)
area = (3.14 + 64/2)
area = ( 3.78 / 2)
area = 1.89 sq in
Question 23.
CRITICAL THINKING
How can you add a figure to a composite figure without increasing its perimeter? Can this be done for all figures? Draw a diagram to support your answer.
Answer:
Explanation:
The perimeter does not increases.
Lesson 9.4 Constructing Polygons
EXPLORATION 1
Using Technology to Draw Polygons
Work with a partner.
a. Use geometry software to draw each polygon with the given side lengths or angle measures, if possible. Complete the table.
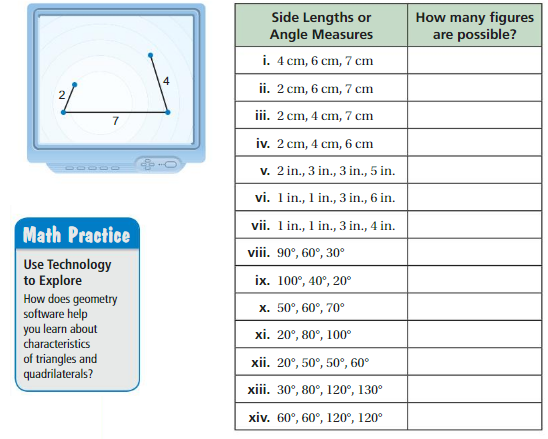
b. Without constructing, how can you tell whether it is possible to draw a triangle given three angle measures? three side lengths? Explain your reasoning.
c. Without constructing, how can you tell whether it is possible to draw a quadrilateral given four angle measures? four side lengths? Explain your reasoning.
Answer:
b. Yes it is possible to draw a triangle with the given three angles measures, three side lengths.
c. yes it is possible to draw a quadrilateral with the given 4 angle measures, four side lengths.
Explanation:
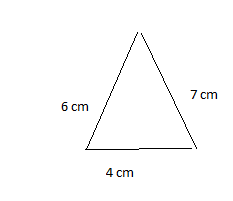
1. given that sides = 4 cm , 6 cm , 7cm
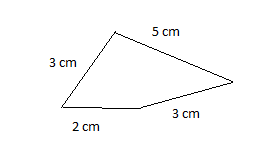
2. given that sides = 2 cm , 3 cm , 3 cm, 5 cm
Try It
Draw a triangle with the given angle measures, if possible.
Question 1.
45°, 45°, 90°
Answer:
Explanation:
The above triangle is an equilateral triangle.
it forms with the given angles 45°, 45°, 90°.
Question 2.
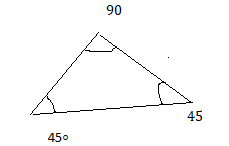
100°, 55°, 25°
Answer:
Explanation:
The above triangle is scalene triangle.
it forms with the given angles 100°, 55°, 25°.
Question 3.
60°, 60°, 80°
Answer:
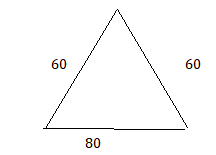
Explanation:
The above triangle is an equilateral triangle.
it forms with the given angles60°, 60°, 80°
Question 4.
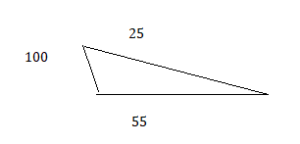
Draw a triangle with side lengths of 1 inch and 2 inches that meet at a 60° angle.
Answer:
Explanation:
The above triangle is a scalene triangle.
it forms with the given angles 60° , 1 inch and 2 inch.
Draw a triangle with the given side lengths, if possible.
Question 5.
2 cm, 2 cm, 5 cm
Answer:
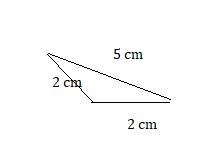
Explanation:
given the sides of a triangle 2cm , 2 cm , 5 cm
Question 6.
4 cm, 3 cm, 3 cm
Answer:
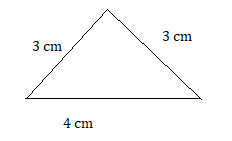
Explanation:
given that 2 sides are same and one side is different.
Question 7.
1 cm, 4 cm, 5 cm
Answer:
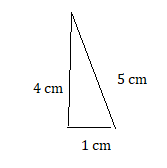
Draw a quadrilateral with the given angle measures, if possible.
Question 8.
100°, 90°, 65°, 105°
Answer:
Explanation:
The quadrilateral formed with the given angles 100°, 90°, 65°, 105°.
Question 9.
100°, 40°, 20°, 20°
Answer:
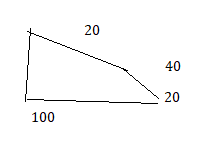
Explanation:
The quadrilateral formed with the given angles 100°, 40°, 20°, 20°.
Question 9.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
DRAWING POLYGONS Draw a polygon with the given side lengths or angle measures, if possible.
Question 10.
25 mm, 36 mm, 38 mm
Answer:
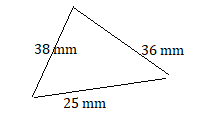
Explanation:
The polygon formed with the given sides is a triangle.
Question 11.
10°, 15°, 155°
Answer:

Explanation:
The polygon formed with the given sides is a triangle.
Question 12.
20°, 45°, 50°, 65°
Answer:
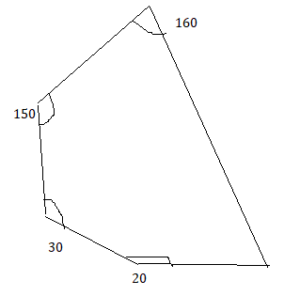
Explanation:
The polygon formed with the given sides is a hexagon.
Question 9.
100°, 40°, 20°, 20°
Answer:

Explanation:
The polygon formed with the given sides is a hexagon.
Question 9.
100°, 40°, 20°, 20°
Answer:

Question 9.
100°, 40°, 20°, 20°
Answer:

Explanation:
The polygon formed with the given sides is a quadrilateral.
Question 13.
50°, 90°, 110°, 110°
Answer:
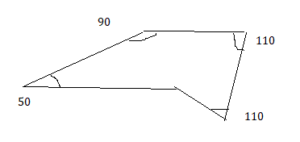
Question 14.
USING SIDE LENGTH
Can you construct one, many, or triangle(s) with side lengths of 3 inches, 4 inches, and 8 inches? Explain.
Answer:
We can construct only one triangle
Explanation:
Given the side lengths of 3 inches, 4 inches, and 8 inches.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 15.
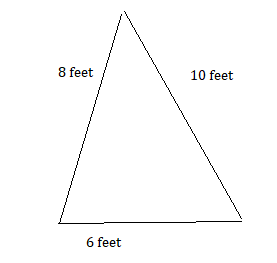
A triangular pen has fence lengths of 6 feet, 8 feet, and 10 feet. Create a scale drawing of the pen.
Answer:
Question 16.
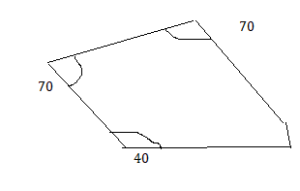
The front of a cabin is the shape of a triangle. The angles of the triangle are 40°, 70°, and 70°. Can you determine the height of the cabin? If not, what information do you need?
Answer:
Question 17.
DIG DEEPER!
Two rooftops have triangular patios. One patio has side lengths of 9 meters,10 meters, and 11 meters.e other has side lengths of 6 meters,10 meters, and 15 meters. Which patio has a greater area? Explain.

Answer:
The patio which has a side length of 6 meters, 10 meters, and 15 meters.
Explanation:
The patio has a greater side length.
Constructing Polygons Homework & Practice 9.4
Review & Refresh
Find the perimeter and area of the figure.
Question 1.
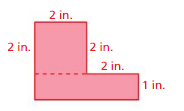
Answer:
area = 12 in
perimeter = 14 in
Explanation:
area of the rectangle = l x w
l = length, w = width
area = 4 x 3
area = 12 in
perimeter of the rectangle = 2 ( l + w)
perimeter = 2 (7)
perimeter = 14 in
Question 2.
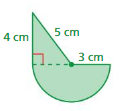
Answer:
perimeter of the figure = 9.48 sq cm
area of the figure = 28.26 sq cm
Explanation:
perimeter of the semicircle = ( π + 2) r
p = (3.14 + 2 ) 3
p = 9.48 cm
area of the figure = π x r x r
area = 3.14 x 3 x3
area = 28.26 sq cm
Use a tree diagram to find the sample space and the total number of possible outcomes of the indicated event.

Question 3.
choosing a toothbrush

Answer:
Extra soft, soft, Medium
Explanation:
In the above given figure the strength of the toothbrush = extra soft , soft , meedium
Question 4.

Answer:
The size of the toy hop is small, medium , large.
Explanation:
given that the colour of the toy hoop is blue , green , orange, pink, purple , yellow.
Concepts, Skills, & Problem Solving
USING TECHNOLOGY TO DRAW POLYGONS Use geometry software to draw the polygon with the given side lengths or angle measures, if possible. (See Exploration 1, p. 381.)
Question 5.
30°, 65°, 85°
Answer:

Question 6.
2 in., 3 in., 5 in.
Answer:

Question 7.
80°, 90°, 100°, 110°
Answer:
Not possible.
Question 8.
2 cm, 2 cm, 5 cm, 5 cm
Answer:
CONSTRUCTING TRIANGLES USING ANGLE MEASURES Draw a triangle with the given angle measures, if possible.
Question 9.
40°, 50°, 90°
Answer:

Question 10.
20°, 40°, 120°
Answer:

Question 11.
38°, 42°, 110°
Answer:

Question 12.
54°, 60°, 66°
Answer:

Question 13.
YOU BE THE TEACHER
Your friend determines whether he can draw a triangle with angle measures of 10°, 40°, and 130°. Is your friend correct? Explain your reasoning.

Answer:
Yes .
Explanation:
yes we cannot draw the triangle with the angle measures of 10, 40, 130
CONSTRUCTING TRIANGLES USING ANGLES AND SIDES Draw a triangle with the given description.
Question 14.
side lengths of 1 inch and 2 inches meet at a 50° angle
Answer:
yes.
Explanation:
we can draw a triangle with 1 inch 2 inch that meets at 50 degrees.
Question 15.
side lengths of 7 centimeters and 9 centimeters meet at a 120° angle
Answer:
yes.
Explanation:
we can draw a triangle with 7 cm 9 cm that meets at 120 degrees.
Question 16.
a 95° angle connects to a 15° angle by a side of length 2 inches
Answer:
no.
Explanation:
we cannot draw a triangle with 2 inches 15 degrees that meets at 120 degrees.
Question 17.
a 70° angle connects to a 70° angle by a side of length 4 centimeters
Answer:
yes.
Explanation:
we can draw an angle with 4 cm 70 degrees that meets at 120 degrees.
CONSTRUCTING TRIANGLES USING SIDE LENGTHS Draw a triangle with the given side lengths, if possible.
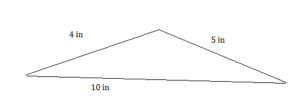
Question 18.
4 in., 5 in., 10 in.
Answer:
Question 19.
10 mm, 30 mm, 50 mm
Answer:

Question 20.
5 cm, 5 cm, 8 cm
Answer:
Question 21.
8 mm, 12 mm, 13 mm
Answer:
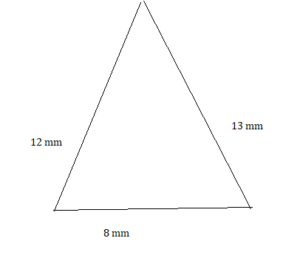
Question 22.
MODELING REAL LIFE
Can you construct a triangular case using two pieces of wood that are 12 inches long and one piece of wood that is 25 inches long? Explain.
Answer:
Yes we can construct a triangle .
Explanation:
We can costruct the triangle by using two pieces of wood that are 12 inches long and the one piece of wood is 25 inches.
Question 23.
MODELING REAL LIFE
Can you construct a warning triangle using three pieces of plastic that are each 6 inches long? Explain.

Answer:
Yes.
Explanation:
we can construct the three pieces of plastic by using 3 6 inches long.
Question 24.
LOGIC
You are constructing a triangle. You draw the first angle, as shown. Your friend says that you must be constructing an acute triangle. Is your friend correct? Explain your reasoning.
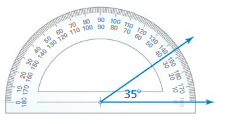
Answer:
Yes my friend is correct.
Explanation:
it is a acute angle triangle.
USING ANGLES AND SIDES Determine whether you can construct one, many, or no triangle(s) with the given description. Explain your reasoning.
Question 25.
a triangle with one angle measure of 60and one side length of 4 centimeters
Answer:
Explanation:
we cannot construct one trinangle with the help of given sidelengths.
Question 26.
a scalene triangle with side lengths of 3 centimeters and 7 centimeters
Answer:

Question 27.
an isosceles triangle with two side lengths of 4 inches that meet at an 80° angle
Answer:
Question 28.
a triangle with one angle measure of 60°, one angle measure of 70°, and a side length of 10 centimeters between the two angles
Answer:
Question 29.
a triangle with one angle measure of 20°, one angle measure of 35°, and a side of length 3 inches that is between the two angles
Answer:
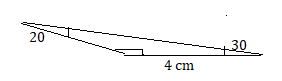
Question 29.
REASONING
A triangle is shown.
a. Construct a triangle with side lengths twice those of the triangle shown. Does the new triangle have the same angle measures?
b. How can you change the side lengths of the triangle so that the measure of ∠A increases?
Answer:
a. Yes the new triangle have the same angle.
b. angle A increases .
Explanation:
Given that the triangle with side lengths twice those of the triangle shown.
If we can change the side lengths of triangle .
CONSTRUCTING QUADRILATERALS Draw a quadrilateral with the given angle measures, if possible.
Question 31.
60°, 60°, 120°, 120°
Answer:
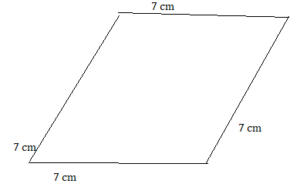
Question 32.
50°, 60°, 110°, 150°
Answer:
Question 33.
20°, 30°, 150°, 160°
Answer:
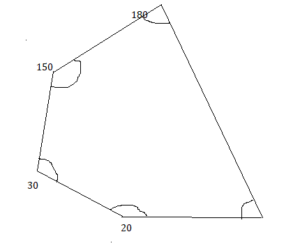
Question 34.
10°, 10°, 10°, 150°
Answer:
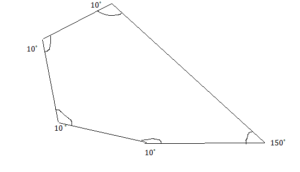
Explanation:
Given angles are 10 degrees, 10 degrees, 10 degrees, 10 degrees.
CONSTRUCTING SPECIAL QUADRILATERALS Construct a quadrilateral with the given description.
Question 35.
a rectangle with side lengths of 1 inch and 2 inches
Answer:
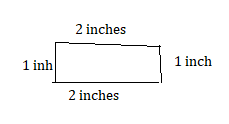
Question 36.
a kite with side lengths of 4 centimeters and 7 centimeters
Answer:
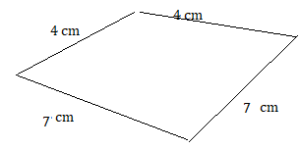
Question 37.
a trapezoid with base angles of 40°
Answer:
A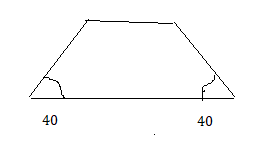 nswer
nswer
Question 38.
a rhombus with side lengths of 10 millimeters
Answer:
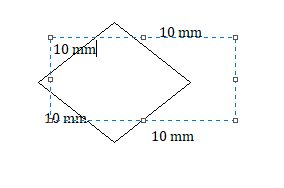
Question 39.
REASONING
A quadrilateral has side lengths of 6 units, 2 units, and 3 units as shown. How many quadrilaterals can be formed given a fourth side with a fixed length? Explain.
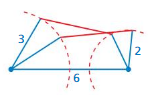
Answer:
2 quadrilaterals can be formed.
Explanation:
Given that the quadrilateral has side lengths of 6 units, 2 units, and 3 units.
so 2 quadrilaterals can be formed.
Question 40.
REASONING
What types of quadrilaterals can you form using four side lengths of 7 units? Use drawings to support your conclusion.
Answer:

Question 41.
MODELING REAL LIFE
A triangular section of a farm is enclosed by fences that are 2 meters, 6 meters, and 7 meters long. Estimate the area of the section.
Answer:
Area of the section = 12 sq meters.
Question 42.
MODELING REAL LIFE
A chemical spill expert sets up a triangular caution zone using cones. Cones A and B are 14 meters apart. Cones B and C are 22 meters apart. Cones A and C are 34 meters apart. Estimate the area of the caution zone.

Answer:
Area of the area of the caution Zone = 308 sq meters.
Explanation:
Area of the triangle = l x b
area = 22 x 14
area = 308 sq meters.
Question 43.
MODELING REAL LIFE
A search region is in the shape of an equilateral triangle. The measure of one side of the region is 20 miles. Make a scale drawing of the search region. Estimate the area of the search region.
Answer:
Explanation:
Given that the equilateral triangle .
Question 44.
REASONING
A triangle has fixed side lengths of 2 and 14.
a. How many triangles can you construct? Use the figure below to explain your reasoning.
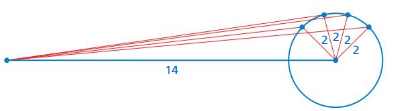
b. Is the unknown side length of the triangle also fixed? Explain.
Answer:
We can construct 14 triangles.
b. No the side length of the triangle cannot fixed.
Explanation:
a. We can construct 14 triangles.
b. No the side length of the triangl cannot fixed.
Lesson 9.5 Finding Unknown Angle Measures
EXPLORATION 1
Using Rules About Angles
Work with a partner. The diagram shows pairs of angles and vertical angles. Vertical angles cannot be adjacent.
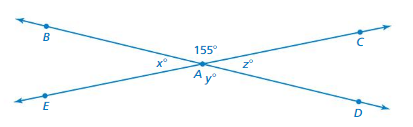
a. Which pair(s) of angles are adjacent angles? Explain.
b. Which pair(s) of angles are vertical angles? Explain.
c. Without using a protractor, find the values of x, y, and z. Explain your reasoning.
d. Make a conjecture about the measures of any two vertical angles.
e. Test your conjecture in part(d) using the diagram below. Explain why your conjecture is or is not true.
Answer:
A. ∠ACD, ∠AEB
b. ∠ACD, ∠AEB
c. 125
d. ∠ACD, ∠AEB

Try It
Question 1.
Name a pair of (a) adjacent angles, (b) complementary angles, (c) supplementary angles, and (d) vertical angles in the figure.
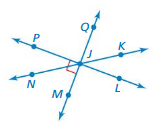
Answer:
a. ∠JKL, ∠JKQ, . ∠MNJ,. ∠PJN
b. ∠JKQ
c. ∠JNK, ∠ JPL. ∠JMQ
D. ∠JMQ, ∠JPL.
Explanation:
The above angles are adjacent, vertical, supplementary,complementary.
Classify the pair of angles. Then find the value of x.
Question 2.
Answer:
x = 95 ˚
Explanation:
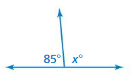
x = (180 – 85)
x = 95 ˚
Question 3.
Answer:
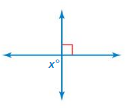
x = 180 ˚
Explanation:
x = 180 ˚
Question 4.
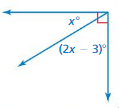
Answer:
x = 30 ˚
Explanation:
(2x – 3) = 60
2x = (60/3)
2x = 20
x = 10
Find the measure of the indicated angle in the diagram.
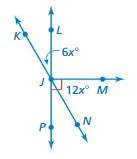
Question 5.
∠NJM
Answer:
12 x ˚
Question 6.
∠KJP
Answer:
16 x ˚
Question 7.
∠KJM
Answer:
6x ˚
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
NAMING ANGLES
Name a pair of (a) adjacent angles, (b) complementary angles, (c) supplementary angles, and (d) vertical angles in the figure at the left.
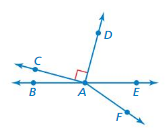
Answer:
a. ∠ABC
b. ∠ABD
c. ∠ABE
d. ∠ABE
Explanation:
The above angles are adjacent, vertical, supplementary,complementary.
FINDING ANGLE MEASURES Find the value of x.
Question 9.
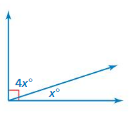
Answer:
x = 60˚
Explanation:
4x = x
4x – x = 180
3x = 180
x = 60˚
Question 10.
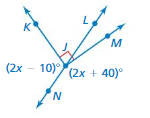
Answer:
x = 12.5˚
Explanation:
2x – 10= 2x + 40
4x = 50
x = 12.5˚
Question 11.
WHICH ONE DOESN’T BELONG?
Which pair of angles does not belong with the other three? Explain your reasoning.

Answer:
∠FBA, ∠EBD does not belong with the other three.
Explanation:
the 3 angles are different measures,
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
What is the angle between any two windmill blades in the windmill at the left? Justify your answer.

Answer:
The angle between any two wind mills blades in the windmill at the left = 60 °
Explanation:
60 + 60 + 60 = 180
Question 13.
A hockey puck strikes a wall at an angle of 30°. The puck then travels away from the wall at the same angle. Find the value of y. Explain your reasoning.
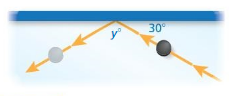
Answer:
y = 150 °
Explanation:
In the above figure said that hockey puck strikes a wall at an angle of 30 °.
so 180 – 30 = 150
Question 14.
DIG DEEPER!
The laptop screen turns off when the angle between the keyboard and the screen is less than 20°. How many more degrees can the laptop screen close before the screen turns off?

Answer:
The laptop screen close before the screen turns off = 60 degrees.
Explanation:
(z + 40) = (z – 20)
z – z = (- 20 -40)
z = -60
Finding Unknown Angle Measures Homework & Practice 9.5
Review & Refresh
Draw a triangle with the given side lengths, if possible.
Question 1.
1 in., 3 in., 4 in.
Answer:
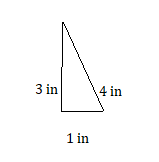
Explanation:
In the above question , they said to draw 1 in, 3 in, 4 in.
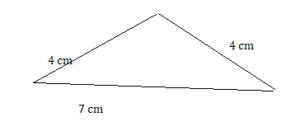
Question 2.
4 cm, 4 cm, 7 cm
Answer:
Solve the inequality. Graph the solution.
Question 3.
– 8y ≤ 40
Answer:
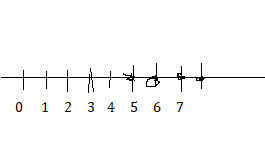
Explanation:
– 8y ≤ 40
y = (40/8)
y = 5
Question 4.
1.1z > – 3.3
Answer:
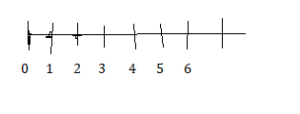
Explanation:
z = 3.3
Question 5.
\(\frac{1}{3}\)x ≥ 2.5
Answer:
Concepts, Skills, & Problem Solving
USING RULES ABOUT ANGLES The diagram shows pairs of adjacent vertical angles and angles. B(See Exploration 1, p. 389.)
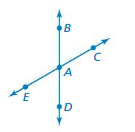
Question 6.
Which pair(s) of angles are adjacent angles? Explain.
Answer:
angle AEC, angle ABD.
Explanation:
In the above given figure angle AEC, angle ABD are adjacent.
Question 7.
Which pair(s) of angles are vertical angles? Explain.
Answer:
angle ABC, angle ADE
Explanation:
In the above given figure angle AEC, angle ABD are adjacent.
NAMING ANGLES Use the figure shown.
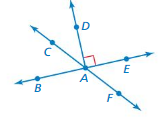
Question 8.
Name a pair of adjacent angles.
Answer:
∠ADC, ∠AEF, ∠ABC
Question 9.
Name a pair of complementary angles.
Answer:
∠ADE, ∠ABD
Question 10.
Name a pair of supplementary angles.
Answer:
∠ABE, ∠ACF
Question 11.
Name a pair of vertical angles.
Answer:
∠AEF, ∠ABC
Question 12.
YOU BE THE TEACHER
Your friend names a pair of angles with the same measure. Is your friend correct? Explain your reasoning.
Answer:
yes my friend is correct
Explanation:
The angles both have the same measure.
ADJACENT AND VERTICAL ANGLES Tell whether the angles are adjacent, vertical, or neither. Explain.
Question 13.
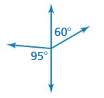
Answer:
vertical.
Explanation:
The given angles are vertical.
Question 14.
Answer:
Adjacent.
Explanation:
The given angles are adjacent.
Question 15.
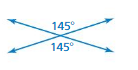
Answer:
Adjacent, vertical
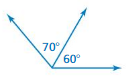
Explanation:
The given angles are adjacent, vertical.
COMPLEMENTARY AND SUPPLEMENTARY ANGLES Tell whether the angles are complementary supplementary, or neither. Explain.
Question 16.
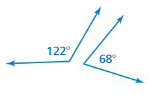
Answer:
The angles are neither complementary nor supplementary.
Explanation:
complementary = 90 degree
supplementary = 180 degree
Question 17.
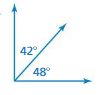
Answer:
The angles are complementary.
Explanation:
complementary = 90 degree
supplementary = 180 degree
Question 18.
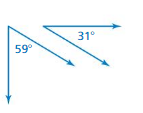
Answer:
The angles are complementary.
Explanation:
complementary = 90 degree
supplementary = 180 degree
Question 19.
YOU BE THE TEACHER
Your friend names a pair of supplementary angles. Is your friend correct? Explain.
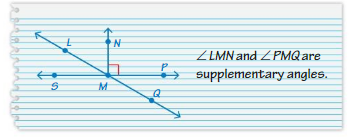
Answer:
yes my friend is correct.
Explanation:
angle LMN and angle PMQ are supplementary angles.
USING PAIRS OF ANGLES Classify the pair of angles. Then find the value of x.
Question 20.
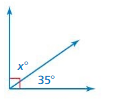
Answer:
Acute angle.
x = 145
Explanation:
x = (180 – 35)
x = 35
Question 21.
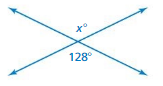
Answer:
verticle angle.
x = 52
Explanation:
x = (180 – 128)
x = 52
Question 22.
Answer:
obtuse angle.
x = 63
Explanation:
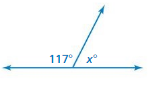
x = (180 – 117)
x = 63
Question 23.
Answer:
intersection angles
x = 25
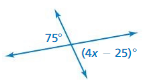
Explanation:
(4x – 25) = 75
4x = 75 + 25
4x = 100
x = (100/4)
x = 25
Question 24.
Answer:
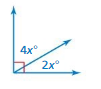
x = 15
Explanation:
2x = 30
x = (30/2)
x = 15
4x = 60
x = (60/4)
x = 15
Question 25.
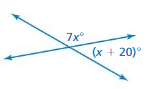
Answer:
x = 3.33
Explanation:
(x + 20 ) = 7 x
20 = 7x – x
20 = 6x
x = (20/6)
x = 3.33
Question 26.
Answer:
x = 15
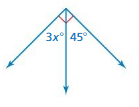
Explanation:
3x = 45
x = (45/3)
x = 15
Question 27.
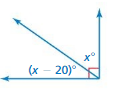
Answer:
x = 20
Explanation:
(x – 20 ) = x
20 = x – x
x = 20
Question 28.
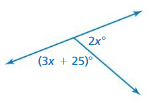
Answer:
x = 25
Explanation:
(3x + 25) = 2x
3x – 2x = 25
x = 25
Question 29.
MODELING REAL LIFE
What is the measure of each angle formed by the intersection? Explain.
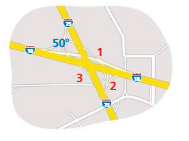
Answer:
angle 2 = 50°
angle 3 = 40°
angle 1 = 40°
Explanation:
In the above figure the angle 4 is given.
Question 30.
MODELING REAL LIFE
A tributary joins a river at an angle x. Find the value of x. Explain.
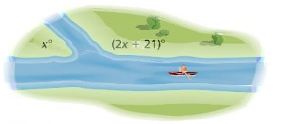
Answer:
x = 21
Explanation:
(2x + 21 ) = x
2x – x = 21
x = 21
Question 31.
MODELING REAL LIFE
The iron cross is a skiing trick in which the tips of the skis are crossed while the skier is airborne. Find the value of x in the iron cross shown.

Answer:
The value of x in the iron cross = 43
Explanation:
(2x + 41) = 127
2x = 127 – 41
2x = 86
x = 43
FINDING ANGLE MEASURES Find all angle measures in the diagram.
Question 32.
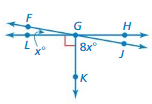
Answer:
x = 90˚
Question 33.
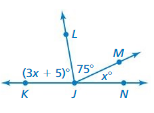
Answer:
23.33
Explanation:
(3x + 5) = 75
3x = 75 – 5
3x = 70
x = (70/3)
x = 23.33
Question 34.
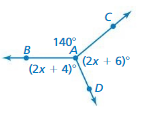
Answer:
x = 68
x = 67
Explanation:
(2x + 4) = 140
2x = (140 – 4)
2x = 136
x = (136/2)
x = 68
(2x + 6) = 140
2x = (140 – 6)
2x = 134
x = (134/2)
x = 67
OPEN-ENDED Draw a pair of adjacent angles with the given description.
Question 35.
Both angles are acute.
Answer:
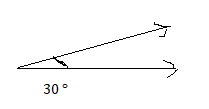
Question 36.
One angle is acute, and one is obtuse.
Answer:
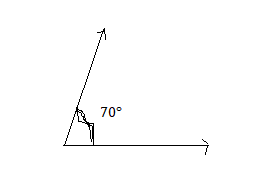
Question 37.
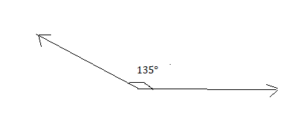
The sum of the angle measures is 135°.
Answer:
REASONING Copy and complete each sentence with always, sometimes, or never.
Question 38.
If x and y are complementary angles, then both x and y are________ acute.
Answer:
Right acute.
Explanation:
if x and y are complimentary then the x and y are right acute.
Question 39.
If x and y are supplementary angles, then is x ________ acute.
Answer:
left acute.
Explanation:
if x and y are complimentary then the x and y are right acute.
Question 40.
If x is a right angle, then is x ________ acute.
Answer:
Right acute.
Explanation:
if x and y are complimentary then the x and y are right acute.
Question 41.
If x and y are complementary angles, then x and y are ________ adjacent.
Answer:
Right adjacent.
Explanation:
if x and y are complimentary then the x and y are right adjacent.
Question 42.
If x and y are supplementary angles, then x and y are _______ vertical.
Answer:
left vertical.
Explanation:
if x and y are supplementary then the x and y are left vertical.
Question 43.
REASONING
Draw a figure in which ∠1 and ∠2 are acute vertical angles, ∠3 is a right angle adjacent to ∠2, and the sum of the measure of ∠1 and the measure of ∠4 is 180°.
Answer:

Question 44.
STRUCTURE
Describe the relationship between the two angles represented by the graph shown at the right.
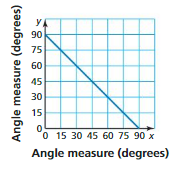
Answer:
90°
Explanation:
The relationship between the two angles represented by the graph =90°
Question 45.
STRUCTURE
Consider the figure shown at the left. Use a ruler to extend both rays into lines. What do you notice about the three new angles that are formed?
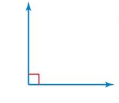
Answer:
The 3 angles that are formed = 30°, 60°, 90°
Explanation:
The given angles are right angles.
Question 46.
OPEN-ENDED
Give an example of an angle that can be a supplementary angle but cannot be a complementary angle to another angle. Explain.
Answer:
Acute angle
Question 47.
MODELING REAL LIFE
The vanishing point of the picture is represented by point B.

a. The measure of ∠ABD is 6.2 times greater than the measure of ∠CBD. Find the measure of ∠CBD.
b. ∠FBE and ∠EBD are congruent. Find the measure of ∠FBE.
Answer:
a. The measure of ∠CBD = 30°
b. The measure of ∠FBE = 60°
Explanation:
Given that the measure of ∠ABD is 6.2 times greater than the measure of ∠CBD = 30°
∠FBE and ∠EBD are congruent so ∠FBE = 60°
Question 48.
CRITICAL THINKING
The measures of two complementary angles have a ratio of 3 : 2. What is the measure of the larger angle?
Answer:
The measure of the larger angle = 3
Explanation:
given that, the measures of two complementary angles have a ratio = 3 : 2
Question 49.
REASONING
Two angles are vertical angles. What are their measures if they are also complementary angles? supplementary angles?
Answer:
when two angles are vertical.
complementary angles = Two angles are called complementary when their measures add to 90°
supplementary angles = two angles are called supplementary when their measures add to 180°
Question 50.
PROBLEM SOLVING
Find the values of x and y.
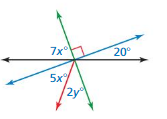
Answer:
x = 2.857
y = 2
x = 4
Explanation:
7 x = 20
x = (20/7)
x = 2.857
2y = 20
y = (20/10)
y = 2
5x = 20
x = (20/5)
x = 4
Geometric Shapes and Angles Connecting Concepts
Using the Problem-Solving Plan
Question 1.
A dart is equally likely to hit any point on the board shown. Find the theoretical probability that a dart hitting the board scores 100 points.
Understand the problem.
You are given the dimensions of a circular dartboard. You are asked to find the theoretical probability of hitting the center circle.
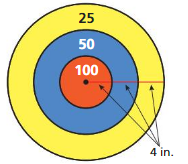
Make a plan.
Find the area of the center circle and the area of the entire dart board. To find the theoretical probability of scoring 100 points, divide the area of the center circle by the area of the entire dart board.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
Area of center =31,400 sq in
area of entire dart board = 1,962.5 sq in
Explanation:
Area of center circle = π r ²
a = 3.14 x 100 x 100
a = 31,400 sq in
area of entire dart board = π r ²
a = 3.14 x 25 x 25
a = 3.14 x 625
a = 1,962.5 sq in
Question 2.
A scale drawing of a window is shown. Find the perimeter and the area of the actual window. Justify your answer.
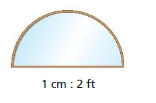
Answer:
Area of semicircle = 1.695sq ft
perimeter of semicircle = 1.58 sq ft
Explanation:
area of the semicircle = ( π + r x r /2)
s . c = (3.14 + 0.5 x 0.5 /2)
s. c = (3.14 + 0.25 /2)
s . c = (3.39 /2
s. c = 1.695 sq ft
perimeter of the semicircle = (π + 2 ) x r
p= 3.14 + 2 x 0.5
p = 3.16 x 0.5
p = 1.58 sq ft
Question 3.
∠CAD makes up 20% of a pair of supplementary angles. Find the measure of ∠DAE. Justify your answer.
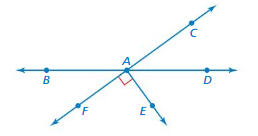
Answer:
∠DAE = 30 %
Explanation:
Given that ∠CAD = 20%
so
∠DAE = 30 %
Performance Task
Finding the Area and Perimeter of a Track
At the beginning of the this chapter, you watched a STEAM video called “Track and Field”. You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Geometric Shapes and Angles Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.
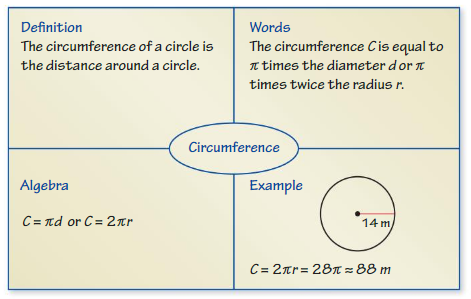
Graphic Organizers
You can use a Four Square to organize information about a concept. Each of the four squares can be a category, such as definition, vocabulary, example, non-example, words, algebra, table, numbers, visual, graph, or equation. Here is an example of a Four Square for circumference.
Choose and complete a graphic organizer to help you study each topic.

1. area of a circle
2. semicircle
3. composite figure
4. constructing triangles
5. constructing quadrilaterals
6. complementary angles
7. supplementary angles
8. vertical angles
Answer:
1. area of a circle = π r ²
2. semicircle = ( π + r ²/2)
3. composite figure = The figure that consists of two or more geometric shapes.
4. constructing triangles = A triangle is a 3 – sided polygon made up of three sides having 3 angles.
5. constructing quadrilateral = quadrilateral can be categorized by the lengths of its sides and the size of its angles.
6. complementary angles = Two angles are called complimentary when their measures add to 90°
7. supplementary angles = two angles are called supplementary when their measures add to 180°
8. vertical angles = The angles opposite each other when two lines cross.
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

9.1 Circles and Circumference (pp. 361–368)
Learning Target: Find the circumference of a circle.
Question 1.
What is the radius of a circular lid with a diameter of 5 centimeters?
Answer:
radius = 50 mm
Explanation:
radius = ( d / 2)
radius = (5/ 2) cm
r = 2.5 cm
Question 2.
The radius of a circle is 25 millimeters. Find the diameter.
Answer:
Diameter = 50 mm
Explanation:
diameter = 2 x radius
diameter = 2 x 25 mm
d = 50 mm
Find the circumference of the object. Use 3.14 or \(\frac{22}{7}\) for π.
Question 3.
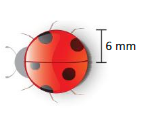
Answer:
circumference of the object = 37.68 sq mm
Explanation:
D. circumference of the circle =2πr
circle = 2 x 3.14 x 6 where r =6 given
circle = 6.28 x 6
circle =37.68 sq mm
Question 4.

Answer:
circumference of the object = 4.71 sq ft
Explanation:
D. circumference of the circle =2πr
circle = 2 x 3.14 x 0.75 where r =0.75 given
circle = 6.28 x 0.75
circle =4.71 sq ft
Question 5.
Answer:
circumference of the object = 4.71 sq cm
Explanation:
D. circumference of the circle =2πr
circle = 2 x 3.14 x 3 .5 where r =3.5 given
circle = 6.28 x 3.5
circle =21.98 sq cm
Question 6.
You are placing non-slip tape along the perimeter of the bottom of a semicircle-shaped doormat. How much tape will you save applying the tape to the perimeter of the inside semicircle of the doormat? Justify your answer.

Answer:
the tape saved = 47 .4 sq in
Explanation:
perimeter of the semicircle = ( π + 2 ) r
p = ( 3.14 + 2) 15
p = (3 .16 ) 15
p = 47.4 sq in
Question 7.
You need to carry a circular cake through a 32-inch wide doorway without tilting it. The circumference of the cake is 100 inches. Will the cake fit through the doorway? Explain.
Answer:
yes the cake fit through the doorway.
Explanation:
radius of the circle = (c/2π)
r= (100/6.28)
r = 15.923 sq in
Question 8.
Estimate the radius of the Big Ben clock face in London.
Answer:
Radius of the Big Ben clock = 7.0063 m
Explanation:
radius of the circle = (c/2π)
r= (44/6.28)
r = 7.0063 m
Question 9.
Describe and solve a real-life problem that involves finding the circumference of a circle.
Answer:
The circumference of a circle = 2 π r
Explanation:
circle = 2 π r
where r = radius , π = 3.14
9.2 Areas of Circles (pp. 369-374)
Learning Target: Find the area of a circle.
Find the area of the circle. Use 3.14 or \(\frac{22}{7}\) for π.
Question 10.
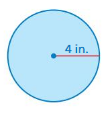
Answer:
The area of the circle = 50.24 sq in
Explanation:
Area of the circle = π x r x r
area = 3.14 x 4 x 4
area = 3.14 x 16
area = 50.24 sq in
Question 11.
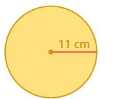
Answer:
The area of the circle = 379.94 sq cm
Explanation:
Area of the circle = π x r x r
area = 3.14 x 11 x 11
area = 3.14 x 121
area = 379.94 sq cm
Question 12.
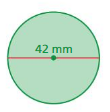
Answer:
The area of the circle = 1384.74 sq mm
Explanation:
Area of the circle = π x r x r
area = 3.14 x 21 x 21
area = 3.14 x 441
area = 1384.74 sq mm
Question 13.
A desktop is shaped like a semicircle with a diameter of 28 inches. What is the area of the desktop?
Answer:
The area of the desktop = 615.44 sq in
Explanation:
Area of the desktop = π x r x r
area = 3.14 x 14 x 14
area = 3.14 x 196
area = 615.44 sq in
Question 14.
An ecologist is studying an algal bloom that has formed on the entire surface of a circular pond. What is the area of the surface of the pond covered by the algal bloom?

Answer:
The area of the surface of the pond covered by the algol bloom = 615.44 ft
Explanation:
Area of the pond = π x r x r
area = 3.14 x 14 x 14
area = 3.14 x 196
area = 615.44 sq ft
Question 15.
A knitted pot holder is shaped like a circle. Its radius is 3.5 inches. What is its area?
Answer:
The area of the pot holder = 38.465 sq in
Explanation:
Area of the pot holder = π x r x r
area = 3.14 x 3.5 x 3.5
area = 3.14 x 12.25
area = 38.465 sq in
9.3 Perimeters and Areas of Composite Figures (pp. 375–380)
Learning Target: Find perimeters and areas of composite figures.
Find the perimeter and the area of the figure.
Question 16.
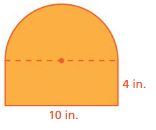
Answer:
Area of semicircle = 1.695 sq in
perimeter of semicircle = 15.8 sq in
Explanation:
area of the semicircle = ( π + r x r /2)
s . c = (3.14 + 5 x 5 /2)
s. c = (3.14 + 25/2)
s . c = (3.39 /2 )
s. c = 1.695 sq in
perimeter of the semicircle = (π + 2 ) x r
p= 3.14 + 2 x 5
p = 3.16 x 5
p = 15.8 sq in
Question 17.
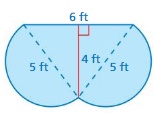
Answer:
Area of semicircle = 6.07 sq ft
perimeter of semicircle = 9.48 sqft
Explanation:
area of the semicircle = ( π + r x r /2)
s . c = (3.14 + 3 x 3 /2)
s. c = (3.14 + 9/2)
s . c = (12.14 /2 )
s. c = 6.07 sq ft
perimeter of the semicircle = (π + 2 ) x r
p= 3.14 + 2 x 3
p = 3.16 x 3
p = 9.48 sq ft
Question 18.
GARDEN
You want to fence part of a yard to make a vegetable garden. How many feet of fencing do you need to surround the garden?
Answer:
The fencing need to surround the garden = 32 sq feet
Explanation:
area of the rectangle = l + b
area = 18 + 14
area = 32 sq feet
9.4 Constructing Polygons (pp. 381-388)
Learning Target: Construct a polygon with given measures.
Draw a triangle with the given description, if possible.
Question 19.
a triangle with angle measures of 15°, 75°, and 90°
Answer:
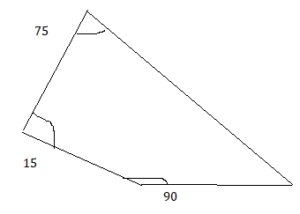
Explanation:
Given triangle with angle measures.
Question 20.
a triangle with a 3-inch side and a 4-inch side that meet at a 30° angle
Answer:
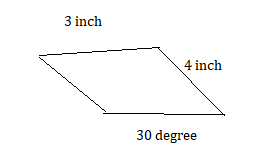
Question 21.
a triangle with side lengths of 5 centimeters, 8 centimeters, and 2 centimeters
Answer:
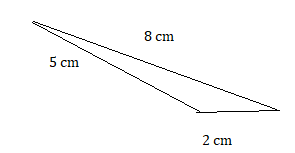
Draw a quadrilateral with the given angle measures, if possible.
Question 22.
110°, 80°, 70°, 100°
Answer:
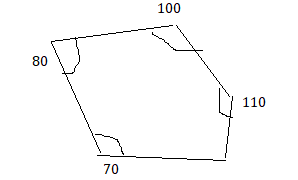
Question 23.
105°, 15°, 20°, 40°
Answer:
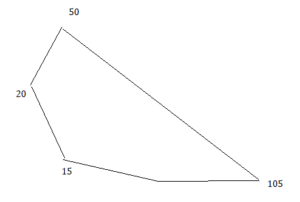
9.5 Finding Unknown Angle Measures (pp. 389–396)
Learning Target: Use facts about angle relationships to find unknown angle measures.
Use the figure shown.
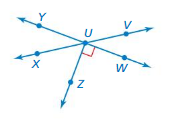
Question 24.
Name a pair of adjacent angles.
Answer:
x , y , v , w .
Explanation:
In the above-given figure, the adjacent angles are x, y, v, w.
Question 25.
Name a pair of complementary angles.
Answer:
u and z
Explanation:
complementary angles = u , z
Question 26.
Name a pair of supplementary angles.
Answer:
x , y , v , z
Explanation:
supplementary are x , y , v , z
Question 27.
Name a pair of vertical angles.
Answer:
x , y , v, w
Explanation:
pair of vertical angles are x , y , v , w
Classify the pair of angles. Then find the value of x.
Question 28.
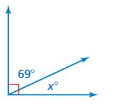
Answer:
x = 111 degrees.
Explanation :
x = 56
x =180 – 69
x = 111 degree
Question 29.
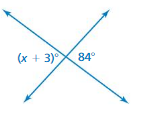
Answer:
x = 81 degrees.
Explanation :
x + 3 = 84
x =84 – 3
x = 81 degree
Question 30.
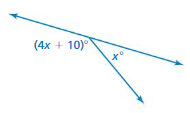
Answer:
x = 3.33degrees.
Explanation :
(4x + 10) = x
10 = x – 4 x
3 x = 10
x = 3.33 degree
Question 31.
Describe two ways to find the measure of ∠2.
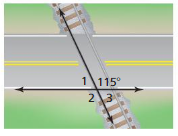
Answer:
angle 2 = 65
Explanation:
x = 180 – 115
x = 65
2 = 65
Question 32.
Using the diagram from Exercises 24–27, find all the angle measures when ∠XUY = 40°.
Answer:
Geometric Shapes and Angles Practice Test
Question 1.
Find the radius of a circle with a diameter of 17 inches.
Answer:
radius of a circle = 8.5 in
Explanation:
radius of a circle = (d / 2)
radius =( 17 / 2)
radius = 8.5 in
Find (a) the circumference and (b) the area of the circle. Use 3.14 or \(\frac{22}{7}\) for π.
Question 2.
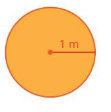
Answer:
Area of the circle = 3.14 m
circumference of the circle = 6.28 m
Explanation:
Area of the circle = π x r x r
area = 3.14 x 1 x 1
area = 3.14 m
circumference of the circle = 2 x π x r
c = 2 x 3.14 x 1
c = 6.28 m
Question 3.
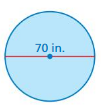
Answer:
Area of the circle = 3846.5 sq in
circumference of the circle = 219. 8 sq in
Explanation:
Area of the circle = π x r x r
area = 3.14 x 35 x 35
area = 3.14 x 1,225 sq in
area = 3846.5 sq in
circumference of the circle = 2 x π x r
c = 2 x 3.14 x 35
c = 6.28 x 35
c = 219.8 sq in
Find (a) the perimeter and (b) the area of the figure. Use 3.14 or \(\frac{22}{7}\) for π.
Question 4.
Answer:
Area of semicircle = 2.695 sq ft
perimeter of semicircle = 4. 74 sq ft
Explanation:
area of the semicircle = ( π + r x r /2)
s . c = (3.14 + 1.5 x 1.5 /2)
s. c = (3.14 + 2.25 /2)
s . c = (5.39 /2 )
s. c = 2.695 sq ft
perimeter of the semicircle = (π + 2 ) x r
p= 3.14 + 2 x 1.5
p = 3.16 x 1.5
p = 4. 74 sq ft
Question 5.
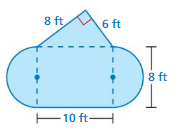
Answer:
Area of semicircle = 9.57 sq ft
perimeter of semicircle = 12.64 sq ft
Explanation:
area of the semicircle = ( π + r x r /2)
s . c = (3.14 + 4 x 4 /2)
s. c = (3.14 + 16 /2)
s . c = (19.14 /2 )
s. c = 9.57 sq ft
perimeter of the semicircle = (π + 2 ) x r
p= 3.14 + 2 x 4
p = 3.16 x 4
p = 12.64 sq ft
Draw a figure with the given description, if possible.
Question 6.
a triangle with sides of length 5 inches and 6 inches that meet at a 50° angle.
Answer:
Question 7.
a triangle with side lengths of 3 inches, 4 inches, and 5 inches
Answer:
Question 8.
a quadrilateral with angle measures of 90°, 110°, 40°, and 120°
Answer:
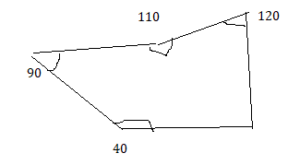
Classify each pair of angles. Then find the value of x.
Question 9.
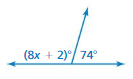
Answer:
x = 9 degrees.
Explanation:
(8x + 2) = 74
8x = 74 – 2
8x = 72
x = (72/8)
x = 9
Question 10.
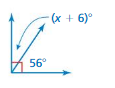
Answer:
x = 50 degrees.
Explanation:
(x + 6) = 56
x = 56 – 6
x = 50
Question 11.
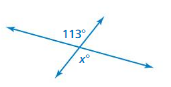
Answer:
x = 67 degrees.
Explanation:
x = 180 – 113
x = 67 degrees.
Question 12.
A museum plans to rope off the perimeter of the 60 ftL-shaped exhibit. How much rope does it need?
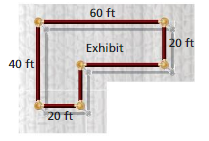
Answer:
Area of the museum = 2,826 sq ft
Explanation:
Area of the museum = π x r x r
area = 3.14 x 30 x 30
area = 3.14 x 900
area = 2,826 sq ft
Geometric Shapes and Angles Cumulative Practice
Question 13.
Draw a pair of adjacent angles that are neither complementary nor supplementary.
Answer:
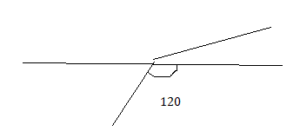
Question 14.
The circumference of a circle is 36.2 centimeters. What is the length of the diameter of the circle?
Answer:
Diameter of the circle = 11.52866 cm
Explanation:
Diameter of the circle = 2 x r
radius of the circle = (c / 2 π )
circumference = 36.2 cm
radius = (36.2 / 6.28)
radius = 5.7643
daimeter = 2 x r
diameter = 5.7643 x 2
diameter = 11.52866 cm
Question 15.
The circular rug is placed on a square floor. The rug touches all four walls. How much of the floor space is not covered by the rug?

Answer:
Area of the circle = 176.625sq ft
Explanation:
Area of the circle = π x r x r
area = 3.14 x 7.5 x 7.5
area = 3.14 x 56.25
area = 176.625 sq ft
Geometric Shapes and Angles Cumulative Practice

Question 1.
To make 6 servings of soup, you need 5 cup of chicken broth. You want to know how many servings you can make with 2 quarts of chicken broth. Which proportion should you use?
A. \(\frac{6}{5}=\frac{2}{x}\)
B. \(\frac{6}{5}=\frac{x}{2}\)
C. \(\frac{6}{5}=\frac{x}{8}\)
D. \(\frac{5}{6}=\frac{x}{8}\)
Answer:
option B is correct.
Explanation:
Given that in the question to make 6 servings of soup you need 5 cup of chicken broth.
Question 2.
What is the value of x?
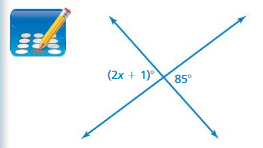
Answer:
x = 42 degrees.
Explanation:
(2x + 1) = 85
2x = 85 – 1
2x = 84
x = (84/2)
x = 42
Question 3.
Your mathematics teacher described an inequality in words.

Which inequality matches your mathematics teacher’s description?
F. 7n – 5 < 42 G. (7 – 5)n > 42
H. 5 – 7n > 42
I. 7n – 5 > 42
Answer:
option G is correct.
Explanation:
5 is less than the product of 7 and an unknown number is greater than 42.
(7 – 5)n > 42
Question 4.
What is the approximate area of the circle below? (Use \(\frac{22}{7}\) for π).
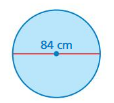
A. 132 cm2
B. 264 cm2
C. 5544 cm2
D. 22,176 cm2
Answer:
Area of the circle = 63.585 sq ft
Explanation:
Area of the circle = π x r x r
area = 3.14 x 42 x 42
area = 3.14 x 1,764
area = 5,538.96 cm
Question 5.
You have a 50% chance of selecting a blue marble from Bag A and a 20% chance of selecting a blue marble from Bag B. Use the provided simulation to answer the question, “What is the estimated probability of selecting a blue marble from both bags?”
F. 12%
G. 16%
H. 24%
I. 88%
Answer:
option F is correct.
Explanation:
The digits 1 and 2 in the ones place represent selecting a blue marble from bag B.
The digits 1 through 5 in the tens place represent selecting a blue marble from bag A.
Question 6.
Which proportion represents the problem?
“What number is 12% of 125?”
A. \(\frac{n}{125}=\frac{12}{100}\)
B. \(\frac{12}{125}=\frac{n}{100}\)
C. \(\frac{125}{n}=\frac{12}{100}\)
D. \(\frac{12}{n}=\frac{125}{100}\)
Answer:
option B is correct.
Explanation:
(12/125 ) x 100
(12/5) x 4
Question 7.
What is the approximate perimeter of the figure below? (Use 3.14 for π)
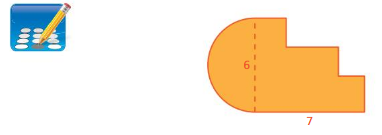
Answer:
The perimeter of the semicircle = 18. 84
Explnation:
perimeter = ( π + 2 x r)
perimeter = (6.28 x 3 )
perimeter = 18 . 84
Question 8.
A savings account earns 2.5% simple interest per year. The principal is $850. What is the balance after 3 years?
F. $63.75
G. $871.25
H. $913.75
J. $7225
Answer:
Question 9.
Two ponds each contain about 400 fish. The double box-and-whisker plot represents the weights of a random sample of 12 fish from each pond. Which statement about the measures of center and variation is true?
A. The variation in the samples is about the same, but the sample from Pond A has a greater median.
B. The variation in the samples is about the same, but the sample from Pond B has a greater median.
C. The measures of center and variation are about the same for both samples.
D. Neither the measures of center nor variation are the same for the samples.
Answer:
option D is correct.
Explanation:
Neither the measures of center nor variation are same for the samples.
Question 10.
A lawn sprinkler sprays water onto part of a circular region, as shown below.

Part A What is the area, in square feet, of the region that the sprinkler sprays with water? Explain your reasoning. (Use 3.14 for π.)
Part B What is the perimeter, in feet, of the region that the sprinkler sprays with water? Explain your reasoning. (Use 3.14 for π.)
Answer:
part A The region that sprinkler sprays with water = 1,256 ft
part B The region that sprinkler sprays with water = 125 .6 ft
Explanation:
area of the circle = π x r x r
area = 3.14 x 20 x 20
area = 1256 ft
perimeter of the circle = 2 x π x r
perimeter = 2 x 3.14 x 20
perimeter = 125. 6 ft
Question 11.
What is the least value of x for which x – 12 ≥ – 8 is true?
F. – 20
G. – 4
H. 4
I. 5
Answer:
option F is correct.
Explanation:
x – 12 ≥ – 8
x = -20
Final Words:
You can download the Big Ideas Math Book 7th Grade Answer Key 9 Geometric Shapes and Angles freely by accessing the direct links presented on this page. Hence hit the links and kickstart your preparation and test yourself by solving the questions in chapter review, practice test, cumulative practice, and overcome your difficulties. All the Best!!!