Big Ideas Math 7th Grade Chapter 3 Expressions Answer Key: Get the free step by step detailed solutions to all Big Ideas Math Grade 7 Chapter 3 Expressions is available here. The solutions for 7th-grade chapter 3 expressions are given in pdf format. So, download Big Ideas Math Book 7th Grade Answer Key Chapter 3 Expressions pdf for free of cost and prepare. By referring to the Big Ideas Math Answers Grade 7 Chapter 3 Expressions you can finish your assignment and homework in time.
Big Ideas Math Book 7th Grade Answer Key Chapter 3 Expressions
The list of topics in the Expressions Chapter are given below. The answers are prepared as per the list of topics in Big Ideas Math Grade 7 Chapter 3 Expressions. Check out the solutions for Algebraic Expressions, Adding and Subtracting Linear Expressions, The Distributive Property, Factoring Expressions are mentioned below. After solving this chapter, you can be able to solve problems using algebraic expressions, identify parts of an algebraic expression, write algebraic expressions, and interpret algebraic expressions in real-life problems.
Performance
Lesson: 1 Algebraic Expressions
Lesson: 2 Adding and Subtracting Linear Expressions
- Lesson 3.2 Adding and Subtracting Linear Expressions
- Adding and Subtracting Linear Expressions Homework & Practice 3.2
Lesson: 3 The Distributive Property
Lesson: 4 Factoring Expressions
Chapter: 3 – Expressions
- Expressions Connecting Concepts
- Expressions Chapter Review
- Expressions Practice Test
- Expressions Cumulative Practice
Expressions STEAM VIDEO/Performance
STEAM Video
Trophic Status
In an ecosystem, energy and nutrients flow between abiotic and components. Biotic components are the living parts of an ecosystem. Abiotic components are the non-living parts of an ecosystem. What is an example of an ecosystem?

Watch the STEAM video “Trophic Status.” Then answer the following questions.
Question 1.
Give examples of both biotic and abiotic components in an ecosystem. Explain.
Answer:
Examples of biotic components are plants, animals, bacteria, fungi. Examples of abiotic components are water, soil, sunlight, gases, etc.
Explanation:
Biotic components are the living organisms in an ecosystem. Examples of biotic components are plants, animals, bacteria, fungi. Abiotic components are the non-living physical and chemical factors in the environment that affect ecosystems. Examples of abiotic components are water, soil, sunlight, gases, etc. Abiotic factors affect the ability of organisms to reproduce, survive, help determine the types and number of organisms able to exist in the environment. Limiting factors restrict growth. Biotic factors are the living things that directly or indirectly affect organisms in the environment.
Question 2.
When an organism is eaten, its energy flows into the organism that consumes it. Explain how to use an expression to represent the total energy that a person gains from eating each of the items shown.

Answer:
bx + lx + fx
Explanation:
Let us take the energy gained by eating a banana is bx, by eating leaves is lx, by eating fish is fx.
So, the expression becomes the sum of all those energies.
bx + lx + fx
Performance Task
Chlorophyll in Plants
After completing this chapter, you will be able to use the STEAM concepts you learned to answer the questions in the Video Performance Task. You will be given the numbers of atoms found in molecules involved in photosynthesis.


You will be asked to determine the total cost for a model of a molecule given the costs of different types of atom models. How can you find the total cost of purchasing several identical objects?
Expressions Getting Ready for Chapter 3
Chapter Exploration
Work with a partner. Rewrite the algebraic expression so that it has fewer symbols x but still has the same value when evaluated for any value of x.

Answer:
1. 3x + 4
2. 3x – 1
3. 2x – 3
4. 2(1 + x)
5. 3x – 1
6. x + 5
Explanation:
1. Original expression is 2x + 4 + x
Simplified expression is 3x + 4
2. Original expression is 3(x + 1) – 4
3x + 3 – 4 = 3x – 1
Simplified expression is 3x – 1
3. Original expression is x – (3 – x)
x – 3 + x
Simplified expression is 2x – 3
4. Original expression is 5 + 2x – 3
Simplified expression is 2 + 2x = 2(1 + x)
5. Original expression is x + 3 + 2x – 4
Simplified expression is 3x – 1
6. Original expression is 2x + 2 – x + 3
Simplified expression is x + 5
Question 7.
WRITING GUIDELINES
Work with a partner. Use your answers in Exercises 1-6 to write guidelines for simplifying an expression.

Answer:
First, you need to take the given original expression as it is.
If there are any braces, then eliminate them by expanding the expression
Then, add or subtract variables and constants together to get the solution
Explanation:
Let us take question 2. 3(x + 1) – 4
Expand 3
3x + 3 – 4
Simplify
3x – 1
APPLYING A DEFINITION
Work with a partner. Two expressions are equivalent if x they have the same value when evaluated for any value of x. Decide which two expressions are equivalent. Explain your reasoning.
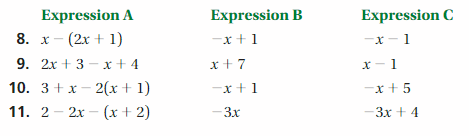
Answer:
8. x – (2x + 1) is equivalent to -x – 1
9. 2x + 3 – x + 4 is equivalent to x + 7 in expression B
10. 3 + x -2(x + 1) is equivalent to -x + 1
11. 2 – 2x – (x + 2) is equivalent to -3x
Explanation:
8. x – (2x + 1) = x – 2x – 1
= -x – 1
So, x – (2x + 1) is equivalent to -x – 1
9. 2x + 3 – x + 4 = x + 7
So, 2x + 3 – x + 4 is equivalent to x + 7 in expression B
10. 3 + x -2(x + 1) = 3 + x -2x – 2
= 1 – x
So, 3 + x -2(x + 1) is equivalent to -x + 1
11. 2 – 2x – (x + 2) = 2 – 2x – x – 2
= -3x
So, 2 – 2x – (x + 2) is equivalent to -3x
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
![]()
Lesson 3.1 Algebraic Expressions
EXPLORATION 1
Simplifying Algebraic Expressions
Work with a partner.
a. Choose a value of other than 0 or 1 for the last column in the table. Complete the table by evaluating each algebraic expression for each value of x. What do you notice?

b. How can you use properties of operations to justify your answers in part(a)? Explain your reasoning.
c. To subtract a number, you can add its opposite. Does a similar rule apply to the terms of an algebraic expression? Explain your reasoning.
Answer:
a. 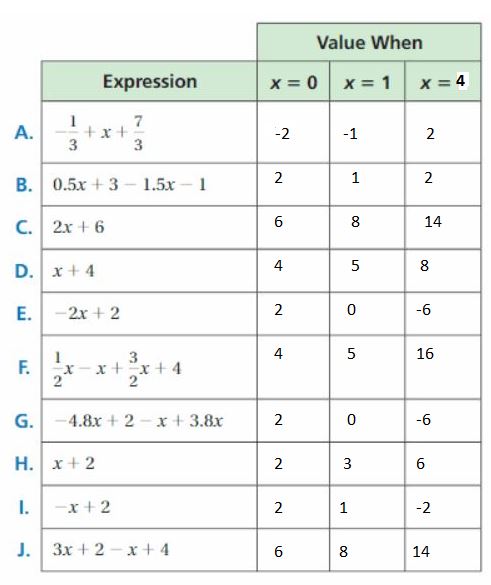
b. Just simplify the expression and put the values of x in simplified expression
c. Yes
Explanation:
a.
A. -1/3 + x + 7/3 = (-1 + 7)/3 + x
= -6/3 + x = -2 + x
If x = 0, then -2 + 0 = -2
If x = 1, then -2 + 1 = -1
If x = 4, then -2 + 4 = 2
B. 0.5x + 3 – 1.5x – 1 = -x + 4
If x = 0, then -0 + 4 = 4
If x = 1, then -1 + 4 = 3
If x = 4, then -4 + 4 = 0
C. 2x + 6
If x = 0, then 2(0) + 6 = 6
If x = 1, then 2(1) + 6 = 8
Ifx = 4, then 2(4) + 6 = 14
D. x + 4
If x = 0, then 0 + 4 = 4
If x = 1, then 1 + 4 = 5
If x = 4, then 4 + 4 = 8
E. -2x + 2
If x = 0, then -2(0) + 2 = 2
If x = 1, then -2(1) + 2 = 0
If x = 4, then -2(4) + 2 = -6
F. 1/2 x – x + 3/2 x + 4 = 4/2 x – x + 4
= 2x – x + 4 = x + 4
If x = 0, then 0 + 4 = 4
If x = 1, then 1 + 4 = 5
If x = 4, then 4 + 4 = 8
G. -4.8x + 2 – x + 3.8x = -2x + 2
If x = 0, then -2(0) + 2 = 2
If x = 1, then -2(1) + 2 = 0
If x = 4, then -2(4) + 2 = -6
H. x + 2
If x = 0, then 0 + 2 = 2
If x = 1, then 1 + 2 = 3
If x = 4, then 4 + 2 = 6
I. -x + 2
If x = 0, then -0 + 2 = 2
If x = 1, then -1 + 2 =1
If x = 4, then -4 + 2 = -2
J. 3x + 2 – x + 4 = 2x + 6
If x = 0, then 2(0) + 6 = 6
If x = 1, then 2(1) + 6 = 8
If x = 4, then 2(4) + 6 = 14
3.1 Lesson
In an algebraic expression, are terms that have the same variables raised to the same exponents. Constant terms are also like terms. To identify terms and like terms in an expression, first write the expression as a sum of its terms.
Try It
Identify the terms and like terms in the expression.
Question 1.
![]()
Answer:
Terms are 10, y, -3/2y, like terms are y, -3/2y.
Explanation:
The given expression is y + 10 – 3/2 y
Like terms are y, -3/2y
Because they have the same variable y
Terms are 10, y, -3/2y
Question 2.
2r2 + 7r – r2 – 9
Answer:
The like terms are 2r², -r², Terms are -9, 7r, 2r², -r²
Explanation:
Given expression is 2r² + 7r -r² – 9
The like terms are 2r², -r²
Terms are -9, 7r, 2r², -r²
Question 3.
7 + 4p – 5 + p + 2q
Answer:
The like terms are 4p, p
The terms are 7, -5, 2q, 4p, p
Explanation:
Given expression is 7 + 4p – 5 + p + 2q
The like terms are 4p, p
The terms are 7, -5, 2q, 4p, p
Try It
Simplify the expression.
Question 4.
-10y + 15y
Answer:
-10y + 15y = 5y
Explanation:
Given expression is -10y + 15y
5y
Question 5.
![]()
Answer:
3/8 b – 3/4 b = -3/8 b
Explanation:
Given expression is 3/8 b – 3/4 b
L.C.M of 8, 4 is 8
(3 – 6)/8 b = -3/8 b
Question 6.
2.4g – 2.4g – 9.8g
Answer:
-9.8g
Explanation:
Given expression is 2.4g – 2.4g – 9.8g
-9.8g
Try It
Simplify the expression.
Question 7.
14 – 3z + 8 + z
Answer:
22 – 2z
Explanation:
Given expression is 14 – 3z + 8 + z
Add constants and like terms
22 – 2z
Question 8.
2.5x + 4.3x – 5
Answer:
6.8x – 5
Explanation:
Given expression is 2.5x + 4.3x – 5
6.8x – 5
Question 9.
2s – 9s + 8t – t
Answer:
7(t – s)
Explanation:
Given expression is 2s – 9s + 8t – t
-7s + 7t = 7(t – s)
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 10.
WRITING
Explain how to identify the terms and like terms of 3y – 4 – 5y.
Answer:
The like terms are 3y, -5y
Terms are -4, 3y, -5y
Explanation:
Given expression is 3y – 4 – 5y
Like terms are the terms in the expression which have the same variable
The following are the like terms because each term contains a variable y and numeric coefficient
3y, -5y
Other than like terms are called the terms
Terms are -4, 3y, -5y
SIMPLIFYING ALGEBRAIC EXPRESSIONS
Simplify the expression.
Question 11.
7p + 6p
Answer:
13p
Explanation:
Given expression is 7p + 6p
13p
Question 12.
![]()
Answer:
3n/2 – 3
Explanation:
Given expression is 4/5 n – 3 + 7/10 n
(8n + 7n)/10 – 3
= 15n/10 – 3
= 3n/2 – 3
Question 13.
2w – g – 7w + 3g
Answer:
-5w + 2g
Explanation:
Given expression is 2w – g – 7w + 3g
Perform the arithmetic operations between the like terms
-5w + 2g
Question 14.
VOCABULARY
Is the expression 3x + 2x – 4 in simplest form? Explain.
Answer:
The expression 3x + 2x – 4 is not in the simplest form.
Explanation:
Given expression is 3x + 2x – 4
= 5x – 4
The simplest form of 3x + 2x – 4 is 5x – 4
Question 15.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.
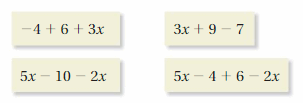
Answer:
5x – 10 – 2x does not belong with the other three.
Explanation:
The first expression is -4 + 6 + 3x = 2 + 3x
The second expression is 3x + 9 – 7 = 3x + 2
The third expression is 5x – 10 – 2x = 3x – 10
Fourth expression is 5x – 4 + 6 – 2x = 3x + 2
So, out of all 5x – 10 – 2x does not belong with the other three.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 16.
MODELING REAL LIFE
An exercise mat is 3.3 times as long as it is wide. Write expressions in simplest form that represent the perimeter and the area of the exercise mat.

Answer:
The perimeter of the exercise mat is 8.6l, Area of the exercise mat is 3.3l²
Explanation:
Let us take the l is the length of the exercise mat
Then, the width of the exercise mat = 3.3l
Perimeter of exercise mat = 2(length + width)
= 2(l + 3.3l)
= 2(4.3l) = 8.6 l
Area of the exercise mat = length x width
= l x 3.3l
= 3.3l²
Therefore, the perimeter of the exercise mat is 8.6l, Area of the exercise mat is 3.3l²
Question 17.
DIG DEEPER!
A group of friends visits the movie theater in Example 4. Each person buys a daytime ticket and a small drink. The group shares 2 large popcorns. What is the average cost per person when there are 4 people in the group?
Answer:
The total cost for a group of 4 people is $35.
Explanation:
Number of tickets . cost per ticket + number of small drinks . cost per small drink + Number of large popcorns . Cost per large popcorn
The same number of tickets, small drinks are purchased. So, can represent the number of tickets, the number of small drinks.
5x + 1.75x + $8 = x(5 + 1.75) + $8
= 6.75x + $8
2 popcorns cost is 2 x 4 = $8
The expression 6.75x + $8 indicates that the cost per person is $6.75 + $8 = 14.75
To find the cost for a group of 4 people, evaluate the expression when x = 4
= 6.75 (4 ) + 8 = 27 + 8 = 35
The total cost for a group of 4 people is $35.
Algebraic Expressions Homework & Practice 3.1
Review & Refresh
Find the product or quotient. Write fractions in simplest form.
Question 1.
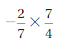
Answer:
-1/2
Explanation:
Given that,
-2/7 x 7/4 = -2/4
= -1/2
Question 2.
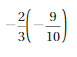
Answer:
3/5
Explanation:
Given that,
-2/3(-9/10) = 2/3 x 9/10
= 6/10 = 3/5
Question 3.
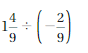
Answer:
-13/6
Explanation:
Given that,
1(4/9) ÷ (-2/3) = 13/9 ÷ (-2/3)
= 13/9 x (-3/2) = -13/6
Order the numbers from least to greatest.
Question 4.
![]()
Answer:
3/4, 78%, 0.85, 87%, 7/8
Explanation:
Given that
7/8 = 0.875, 0.85, 87% = 87/100 = 0.87 3/4 = 0.75, 78% = 78/100 = 0.78
So, the numbers are 0.875, 0.85, 0.87, 0.75, 0.78
Ordering from the least to the greatest is 0.75,0.78,0.85,0.87,0.875
i.e 3/4, 78%, 0.85, 87%, 7/8
Question 5.
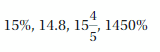
Answer:
15%, 1450%, 14.8, 15(4/5)
Explanation:
Given that,
15% = 15/100 = 0.15, 14.8, 15(4/5) = 79/5 = 15.8, 1450% = 1450/100 = 14.5
So the numbers are 0.15, 14.8, 15.8, 14.5
The order of number from least to greatest is 0.15, 14.5, 14.8, 15.8
i.e 15%, 1450%, 14.8, 15(4/5)
Question 6.
A bird’s nest is 12 feet above the ground. A mole’s den is 12 inches below the ground. What is the difference in height of these two positions?
A. 24 in.
B. 11 ft
C. 13 ft
D. 24 ft
Answer:
The difference in height of these two positions is 13 feet.
Explanation:
Given that,
The bird nest is 12 feet above the ground and a mole’s den is 12 inches below the ground.
So, the mole’s den have to travel 12 inches +12 feet to reach the bird nest
So, the difference in height of these two positions is 12 feet + 12 inches
= 12 feet + 1 feet = 13 feet
Concepts, Skills, & Problem Solving
REASONING
Determine whether the expressions are equivalent. Explain your reasoning. (See Exploration 1, p. 91.)
Question 7.

Answer:
The expressions are not equivalent
Explanation:
Expression 1 is 3 – 5x
Expression 2 is 4.25 – 5x – 4.25
= -5x
So, expressions are not equivalent
Question 8.

Answer:
Both the expressions are equivalent.
Explanation:
Expression 1 is 1.25x + 4 + 0.75x – 3
= 2x + 4 – 3 = 2x + 1
Expression 2 is 2x + 1
So, both the expressions are equivalent.
IDENTIFYING TERMS AND LIKE TERMS
Identify the terms and like terms in the expression.
Question 9.
t + 8 + 3t
Answer:
Like terms are t, 3t
Terms are 8, t, 3t
Explanation:
Given expression is t + 8 + 3t
Like terms are t, 3t
Terms are 8, t, 3t
Question 10.
3z + 4 + 2 + 4z
Answer:
Like terms are 3z, 4z
terms are 4, 2, 3z, 4z
Explanation:
Given expression is 3z + 4 + 2 + 4z
Like terms are 3z, 4z
terms are 4, 2, 3z, 4z
Question 11.
2n – n – 4 + 7n
Answer:
Like terms are 2n, -n, 7n
Terms are -4, 2n, -n, 7n
Explanation:
Given expression is 2n – n – 4 + 7n
Like terms are 2n, -n, 7n
Terms are -4, 2n, -n, 7n
Question 12.
-x – 9x2 + 12x2 + 7
Answer:
Like terms are -9x², 12x²
Terms are 7, -x, -9x², 12x²
Explanation:
Given expression is -x – 9x² + 12x² + 7
Like terms are -9x², 12x²
Terms are 7, -x, -9x², 12x²
Question 13.
1.4y + 5 – 4.2 – 5y2 + z
Answer:
There are no like terms
Terms are 1.4y, 5, -4.2, -5y², z
Explanation:
Given expression is 1.4y + 5 – 4.2 – 5y² + z
There are no like terms
Terms are 1.4y, 5, -4.2, -5y², z
Question 14.
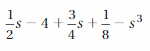
Answer:
Like terms are 1/2 s, 3/4 s
Terms are -4, 1/8, -s³, 1/2 s, 3/4 s
Explanation:
Given expression is 1/2 s – 4 + 3/4 s + 1/8 – s³
Like terms are 1/2 s, 3/4 s
Terms are -4, 1/8, -s³, 1/2 s, 3/4 s
Question 15.
YOU BE THE TEACHER
Your friend identifies the terms and like terms in the expression 3x – 5 – 2x + 9x. Is your friend correct? Explain your reasoning.

Answer:
Wrong
Explanation:
Given expression is 3x – 5 – 2x + 9x
like terms are 3x, -2x, 9x
Terms are 3x, -2x, 9x, 5
SIMPLIFYING ALGEBRAIC EXPRESSIONS
Simplify the expression.
Question 16.
12g + 9g
Answer:
21g
Explanation:
The given expression is 12g + 9g
= 21g
Question 17.
11x + 9 – 7
Answer:
11x + 2
Explanation:
Given expression is 11x + 9 – 7
= 11x + 2
Question 18.
8s – 11s + 6s
Answer:
3s
Explanation:
Given expression is 8s – 11s + 6s
= 14s – 11s = 3s
Question 19.
4b – 24 + 19
Answer:
4b – 5
Explanation:
Given expression is 4b – 24 + 19
= 4b – 5
Question 20.
4p – 5p – 30p
Answer:
-31p
Explanation:
Given expression is 4p – 5p – 30p
= 4p – 35p = -31p
Question 21.
4.2v – 5 – 6.5v
Answer:
-2.3v – 5
Explanation:
Given expression is 4.2v – 5 – 6.5v
= -2.3v – 5
Question 22.
8 + 4a + 6.2 – 9a
Answer:
14.2 – 5a
Explanation:
Given expression is 8 + 4a + 6.2 – 9a
= 14.2 – 5a
Question 23.
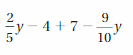
Answer:
3 – 1/2 y
Explanation:
Given expression is 2/5y – 4 + 7 – 9/10y
= (4 – 9)/10 y + 3
= -5/10 y + 3
= -1/2 y + 3
Question 24.
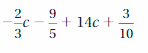
Answer:
40c/3 – 3/2
Explanation:
Given expression is -2/3 c -9/5 + 14c + 3/10
= (-2 + 42)c/3 – (18 – 3)/10
= 40c/3 – 15/10
= 40c/3 – 3/2
Question 25.
MODELING REAL LIFE
On a hike, each hiker carries the items shown. Write and interpret an expression in simplest form that represents the weight carried by x hikers. How much total weight is carried when there are 4 hikers?

Answer:
When there are 4 hikers the total weight is 40.8 lb.
Explanation:
A hiker has thw following items:
A sleeping bag of 3.4 lb weight, camping bag of 4.6 lb weight, and a water bottle of 2.2 lb weight
The expression can be
3.4x + 4.6x + 2.2x = x
Here x is the weight each hiker is carrying
10.2x = x
So, each hiker carries a total weight of 10.2 pounds
When there are 4 hikes, the total weight is 10.2 x 4 = 40.8
Question 26.
STRUCTURE
Evaluate the expression -8x + 5 – 2x – 4 + 5 when x = 2 before and after simplifying. Which method do you prefer? Explain.
Answer:
-14
Explanation:
Given expression is -8x + 5 – 2x – 4 + 5
Put x = 2
-8(2) + 5 -2(2) – 4 + 5
= -16 + 5 – 4 – 4 + 5 = -14
Simplify -8x + 5 – 2x – 4 + 5
= -10x + 10 – 4 = -10x + 6
Put x = 2 in -10x + 6
= -10(2) + 6
= -20 + 6 = -14
I just prefer putting x = 2 after simplifying the expression.
Question 27.
OPEN-ENDED
Write an expression with five different terms that is equivalent 8x2 + 3x2 + 3y. Justify your answer.
Answer:
3x² + 2y + y + 7x² + x²
Explanation:
Given expression is 8x² + 3x² + 3y.
The expression which is equivalent to 8x² + 3x² + 3y and having 5 different terms can be as follows
3x² + 2y + y + 7x² + x²
by simplifying the above expression, you will get the original expression.
Question 28.
STRUCTURE
Which of the following shows a correct way of simplifying 6 + (3 – 5x)? Explain the errors made in the other choices.
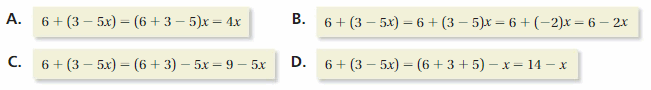
Answer:
C. 6 + (3 – 5x) = (6 + 3) – 5x = 9 – 5x
Explanation:
A. 6 + (3 – 5x) = (6 + 3 – 5)x
Here, x is applicable to only -5x, it is not multiplied with whole expression
B. 6 + (3 – 5x) = 6 + (3 – 5)x
Here, x is the multiple of only -5x, but you have included 3 also which is false
C. 6 + (3 – 5x) = (6 + 3) – 5x = 9 – 5x
This is true
D. 6 + (3 – 5x) = (6 + 3 + 5) – x
5 is the multiple of x, it is not constant.
Question 29.
PRECISION
Two comets orbit the Sun. One comet travels 30,000 miles per hour and the other comet travels 28,500 miles per hour. What is the most efficient way to calculate the difference of the distances traveled by the comets for any given number of minutes? Justify your answer.

Answer:
The difference between those distances is 1500 miles for 60 minutes.
Explanation:
Given that,
One comet travels 30,000 miles per hour and the other comet travels 28,500 miles per hour.
Let us say, the time given for the comets is 60 minutes.
So, in 60 minutes, the first one travels 30,000 miles, and the second one travels 28,500 miles
The difference between those distances = 30,000 – 28,500 = 1500 miles
Question 30.
MODELING REAL LIFE
Find the earnings for washing and waxing 12 cars and 8 trucks. Justify your answer.
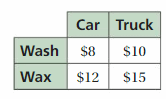
Answer:
and waxing 12 cars and 8 trucks is $440
Explanation:
The earnings for washing and waxing 12 cars = 12(washing one car cost) + 12(waxing one car cost)
= 12($8) + 12($12)
= 12(8 + 12) = $240
The earnings for washing and waxing 8 trucks = 8(washing one truck cost) + 8(waxing one truck cost)
= 8($10) + 8($15)
= 8(10 + 15) = 8(25) = $200
So, the earnings for washing and waxing 12 cars and 8 trucks is $ 240 + $200 = $440
Question 31.
CRITICAL THINKING
You apply gold foil to a piece of red poster board to make the design shown.
a. Find the area of the gold foil when x = 3. Justify your answer.
b. The pattern at the right is called “St. George’s Cross.” Find a country that uses this pattern as its flag.
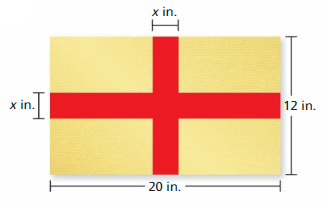
Answer:
a. Area of the gold foil = 87 sq in
b. England
Explanation:
You apply gold foil to a piece of red poster board to make the design.
a. Area of rectangle = length x breadth
= 20 x 12 = 240 sq in.
Length of the gold foil = (12 – x) in
The breadth of gold foil = (20 – x) in
Area of horizontal gold foil = length x breadth
= 20 * x = 20x sq. in
Area of the vertical gold foil = length x breath
= 12 * x = 12x sq. in
Area of the middle gold foil = length x breadth
= x * x = x² sq. in
Area of the gold foil = Area of horizontal gold foil + Area of vertical gold foil – Area of the middle gold foil
= 20x + 12x – x²
The area of gold foil when x = 3 is 20(3) + 12(3) – (3)²
= 60 + 36 – 9
= 87 sq in
b. The pattern at the right is called “St. George’s Cross.” Find a country that uses this pattern as its flag.
England
Question 32.
GEOMETRY
Two rectangles have different dimensions. Each rectangle has a perimeter of (7x + 5) inches. Draw and label diagrams that represent possible dimensions of the rectangles.
Answer:
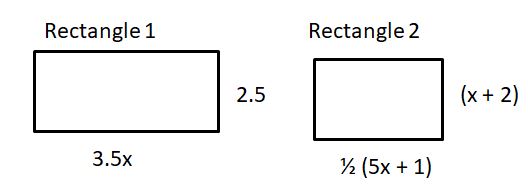
Rectangle 1 dimensions are 3.5x and 2.5, rectangle 2 dimensions are 1/2(5x + 1), x + 2
Explanation:
Perimeter of rectangle = (7x + 5) inches
2(length + width) = 7x + 5
length + width = (7x + 5)/2
Rectangle 1 dimensions can be 3.5x and 2.5
Rectangle 2 dimensions can be 1/2(5x + 1), x + 2
Lesson 3.2 Adding and Subtracting Linear Expressions
EXPLORATION 1
Using Algebra Tiles
Work with a partner. You can use the algebra tiles shown at the left to find sums and differences of algebraic expressions.
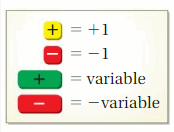
a. How can you use algebra tiles to model a sum of terms that equals 0? Explain your reasoning.
b. Write each sum or difference modeled below. Then use the algebra tiles to simplify the expression.
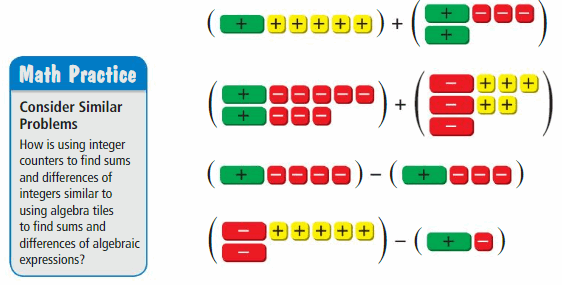
c. Write two algebraic expressions of the form ax + b, where a and b are rational numbers. Find the sum and difference of the expressions.
EXPLORATION 2
Using Properties of Operations
Work with a partner.
a. Do algebraic expressions, such as 2x, -3y, and 3z + 1 have additive inverses? How do you know?
b. How can you find the sums and differences modeled in Exploration 1 without using algebra tiles? Explain your reasoning.
3.2 Lesson
Try It
Find the sum.
Question 1.
(x + 3) + (2x – 1)
Answer:
(x + 3) + (2x – 1) = 3x + 2
Explanation:
The given expression is (x + 3) + (2x – 1)
Add the like terms and constant
= 3x + 3 – 1
= 3x + 2
Question 2.
(-8z + 4) + (8z – 7)
Answer:
(-8z + 4) + (8z – 7) = -3
Explanation:
The given expression is (-8z + 4) + (8z – 7)
= -8z + 4 + 8z – 7
= -3
Question 3.
(4.5 – n) + (-10n + 6.5)
Answer:
(4.5 – n) + (-10n + 6.5) = 11(1 – n)
Explanation:
The given expression is (4.5 – n) + (-10n + 6.5)
= 4.5 – n – 10n + 6.5
= 11 – 11n
= 11(1 – n)
Question 4.
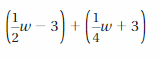
Answer:
(1/2w – 3) + (1/4w + 3) = 3w/4
Explanation:
The given expression is (1/2w – 3) + (1/4w + 3)
= 1/2w – 3 + 1/4w + 3
= (2w + w)/4 = 3w/4
Try It
Find the difference.
Question 5.
(m – 3) – (-m + 12)
Answer:
(m – 3) – (-m + 12) = 2m – 15
Explanation:
The given expression is (m – 3) – (-m + 12)
= m – 3 + m – 12
= 2m – 15
Question 6.
(-2c + 5) – (6.3c + 20)
Answer:
(-2c + 5) – (6.3c + 20) = -83c – 15
Explanation:
The given expression is (-2c + 5) – (6.3c + 20)
= -2c + 5 – 6.3c – 20
= -83c – 15
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
WRITING
Describe how to distinguish a linear expression from a nonlinear expression. Give an example of each.
Answer:
An example of a linear expression is 2x + 1.
An example of a non-linear expression is 2x² + 1
Explanation:
Linear expressions are the expressions where the sum of constants and products of constants and raised to a power of 0 or 1. Non-linear expressions are the expressions where the sum of constants and products of constants and raised to a power that is not 0 or 1.
So, an example of a linear expression is 2x + 1.
An example of a non-linear expression is 2x² + 1
Question 8.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
What is x more than 3x – 1 is different.
Explanation:
What is x more than 3x – 1 = x + 3x – 1 = 4x – 1
Find 3x – 1 decreased by x = 3x – 1 – x = 2x – 1
What is the difference of 3x – 1 and x = 3x – 1 – x = 2x – 1
Subtract (x + 1) from 3x = 3x – (x + 1) = 3x – x – 1 = 2x – 1
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
DIG DEEPER!
In a basketball game, the home team scores (2m + 39) points and the away team scores (3m + 40) points, where m is the number of minutes since halftime. Who wins the game? What is the difference in the scores minutes after halftime? Explain.
Answer:
The away team wins the game. And the difference in the scores minutes after halftime is 2m + 2.
Explanation:
Given that,
The score of home team = 2m + 39 points
The score of away team = 3m + 40 points
Here, m is the number of minutes since halftime
Let us consider the teams that score the same points after the half time
The score of home team = 2m + 39 + 2m + 39 = 4m + 78
The score of away team = 3m + 40 + 3m + 40 = 6m + 80
The difference between those scores = 6m + 80 – (4m + 78)
= 6m + 80 – 4m – 78 = 2m + 2
The away team wins the game.
Question 10.
Electric guitar kits originally cost d dollars online. You buy the kits on sale for 50% of the original price, plus a shipping fee of $4.50 per kit. After painting and assembly, you sell each guitar online for (1.5d + 4.5) dollars. Find and interpret your profit on each guitar sold.
Answer:
Your profit on each electric guitar kit is d dollars
Explanation:
Electric guitar kits originally cost d dollars online.
You buy the kits on sale for 50% of the original price. So, the purchase price of kit is = d/2 + 4.50
After painting and assembly, you sell each guitar online for (1.5d + 4.5) dollars
Profit = Selling price – Purchased price
= 1.5d + 4.5 – (d/2+ 4.50)
= 1.5d + 4.5 – 0.5d – 4.50
= d dollars
Your profit on each electric guitar kit is d dollars. You pay (0.5d + 4.50) dollars for each kit. so, you are getting 4.50 dollars less than double your money.
Adding and Subtracting Linear Expressions Homework & Practice 3.2
Review & Refresh
Simplify the expression.
Question 1.
4f + 11f
Answer:
4f + 11f = 15f
Explanation:
Given expression is 4f + 11f
Add the like terms
= 15f
Question 2.
b + 4b – 9b
Answer:
b + 4b – 9b = -4b
Explanation:
Given expression is b + 4b – 9b
Perform required operations between like terms
= 5b – 9b = -4b
Question 3.
-4z – 6 – 7z + 3
Answer:
-4z – 6 – 7z + 3 = -11z- 3
Explanation:
Given expression is -4z – 6 – 7z + 3
Perform required operations between like terms and constants
= -11z- 3
Evaluate the expression when x = \(-\frac{4}{5}\) and y = \(\frac{1}{3}\).
Question 4.
x + y
Answer:
-7/15
Explanation:
Given expression is x + y
Put x = -4/5, y = 1/3
= -4/5 + 1/3
= (-12 + 5)/15 = -7/15
Question 5.
2x + 6y
Answer:
2/5
Explanation:
Given expression is 2x + 6y
Put x = -4/5, y = 1/3
= 2(-4/5) + 6(1/3) = -8/5 + 6/3
= (-24 + 30)/15 = 6/15
= 2/5
Question 6.
-x + 4y
Answer:
32/15
Explanation:
Given expression is -x + 4y
Put x = -4/5, y = 1/3
= -(-4/5) + 4(1/3)
= 4/5 + 4/3
= (12 + 20)/15
= 32/15
Question 7.
What is the surface area of a cube that has a side length of 5 feet?
A. 25 ft2
B. 75 ft2
C. 125 ft2
D. 150 ft2
Answer:
D. 150 ft²
Explanation:
Given that,
the side length of cube = 5 feet
The surface area of a cube = 6side²
= 6 x (5)² = 6 x 25
= 150 ft²
Concepts, Skills, & Problem Solving
USING ALGEBRA TILES
Write the sum or difference modeled by the algebra tiles. Then use the algebra tiles to simplify the expression. (See Exploration 1, p. 97.)
Question 8.
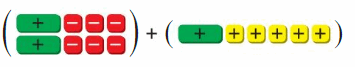
Answer:
3x – 1
Explanation:
Convert the given algebra tiles to the expressions
(x – 1 – 1 – 1 + x – 1 – 1 – 1) + (x + 1 + 1+ 1+ 1+ 1)
= (2x – 6) +(x + 5)
= 2x – 6 + x + 5
= 3x – 1
Question 9.
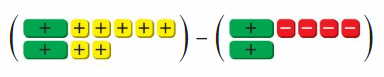
Answer:
11
Explanation:
Convert the given algebra tiles to the expressions
(x + 1 + 1 + 1+ 1 + 1 + x + 1 + 1) – (x – 1 – 1 – 1 – 1 + x)
= (2x + 7) – (2x – 4)
= 2x + 7 – 2x + 4
= 11
ADDING LINEAR EXPRESSIONS
Find the sum.
Question 10.
(n + 8) + (n – 12)
Answer:
(n + 8) + (n – 12) = 2n – 4
Explanation:
Given linear expression is (n + 8) + (n – 12)
= n + 8 + n – 12
= 2n – 4
Question 11.
(7 – b) + (3b + 2)
Answer:
(7 – b) + (3b + 2) = 9 + 2b
Explanation:
Given linear expression is (7 – b) + (3b + 2)
= 7 – b + 3b + 2
= 9 + 2b
Question 12.
(2w – 9) + (-4w – 5)
Answer:
(2w – 9) + (-4w – 5) = -2w – 14
Explanation:
Given linear expression is (2w – 9) + (-4w – 5)
= 2w – 9 – 4w- 5
= -2w – 14
Question 13.
(2x – 6) + (4x – 12)
Answer:
(2x – 6) + (4x – 12) = 8x – 18
Explanation:
Given linear expression is (2x – 6) + (4x – 12)
= 2x – 6 + 4x – 12
= 8x – 18
Question 14.
(-3.4k – 7) + (3k + 21)
Answer:
(-3.4k – 7) + (3k + 21) = -0.4k + 14
Explanation:
Given linear expression is (-3.4k – 7) + (3k + 21)
= -3.4k – 7 + 3k + 21
= -0.4k + 14
Question 15.
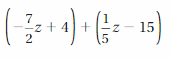
Answer:
(-7/2 z+ 4) + (1/5 z- 15) = -33z/10 – 11
Explanation:
Given linear expression is (-7/2 z+ 4) + (1/5 z- 15)
= -7/2 z + 4 + 1/5 z- 15
= (-35z + 2z)/10 – 11
= -33z/10 – 11
Question 16.
(6 – 2.7h) + (-1.3j – 4)
Answer:
(6 – 2.7h) + (-1.3j – 4) = 2 – 2.7h – 1.3j
Explanation:
Given linear expression is (6 – 2.7h) + (-1.3j – 4)
= 6 – 2.7h – 1.3j – 4
= 2 – 2.7h – 1.3j
Question 17.
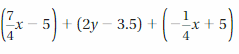
Answer:
(7/4 x – 5) + (2y – 3.5) + (-1/4 x + 5) = 3x/2 + 2y – 3.5
Explanation:
Given linear expression is (7/4 x – 5) + (2y – 3.5) + (-1/4 x + 5)
= 7/4 x – 5 + 2y – 3.5 – 1/4x + 5
= (7x – x)/4 + 2y – 3.5
= 6x/4 + 2y – 3.5
= 3x/2 + 2y – 3.5
Question 18.
MODELING REAL LIFE
While catching fireflies, you and a friend decide to have a competition. After m minutes, you have (3m + 13) fireflies and your friend has (4m + 6) fireflies.
a. How many total fireflies do you and your friend catch? Explain your reasoning.
b. The competition lasts 3 minutes. Who has more fireflies? Justify your answer.

Answer:
a. The total number of fireflies collected is 7m + 19
b. You have more fireflies when compared with your friend.
Explanation:
The number of fireflies you collected after m minutes is (3m + 13)
The number of fireflies your friend collected after m minutes is (4m + 6)
a.
The number of fireflies you collected is (3m + 13)
The number of fireflies your friend collected is (4m + 6)
The total number of fireflies collected = (3m + 13) + (4m + 6)
= 3m + 13 + 4m + 6 = 7m + 19
b. The competition lasts 3 minutes
So, The number of fireflies you collected is 3(1) + 13 = 3 + 13 = 16
The number of fireflies your friend collected is 4(1) + 6 = 4 + 6 = 10
So, you have more fireflies when compared with your friend.
SUBTRACTING LINEAR EXPRESSIONS
Find the difference.
Question 19.
(-2g + 7) – (g + 11)
Answer:
(-2g + 7) – (g + 11) = -3g – 4
Explanation:
The given linear expression is (-2g + 7) – (g + 11)
= -2g + 7 – g – 11
= -3g – 4
Question 20.
(6d + 5) – (2 – 3d)
Answer:
(6d + 5) – (2 – 3d) = 9d + 3
Explanation:
The given linear expression is (6d + 5) – (2 – 3d)
= 6d + 5 – 2 + 3d
= 9d + 3
Question 21.
(4 – 5y) – (2y – 16)
Answer:
(4 – 5y) – (2y – 16) = 20 – 7y
Explanation:
The given linear expression is (4 – 5y) – (2y – 16)
= 4 – 5y – 2y + 16
= 20 – 7y
Question 22.
(2n – 9) – (-2.4n + 4)
Answer:
(2n – 9) – (-2.4n + 4) = 4.4n – 13
Explanation:
The given linear expression is (2n – 9) – (-2.4n + 4)
= 2n – 9 + 2.4n – 4
= 4.4n – 13
Question 23.
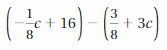
Answer:
(-1/8 c + 16) – (3/8 + 3c) = (-25c + 125)/8
Explanation:
The given linear expression is (-1/8 c + 16) – (3/8 + 3c)
= -1/8 c + 16 – 3/8 – 3c
= (-c – 24c)/8 + (128 – 3)/8
= -25c/8 + 125/8
= (-25c + 125)/8
Question 24.
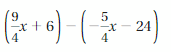
Answer:
(9/4 x + 6) – (-5/4 x – 24) = 7x/2 + 30
Explanation:
The given linear expression is (9/4 x + 6) – (-5/4 x – 24)
= 9x/4 + 6 + 5x/4 + 24
= (9x + 5x)/4 + 30
= 14x/4 + 30
= 7x/2 + 30
Question 25.
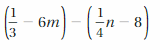
Answer:
(1/3 – 6m) – (1/4 n – 8) = 25/4 – 6m – n/4
Explanation:
The given linear expression is (1/3 – 6m) – (1/4 n – 8)
= 1/3 – 6m – 1/4 n + 8
= (1 + 24)/3 – 6m – n/4
= 25/4 – 6m – n/4
Question 26.
(1 – 5q) – (2.5s + 8) – (0.5q + 6)
Answer:
(1 – 5q) – (2.5s + 8) – (0.5q + 6) = -5.5q – 2.5s – 13
Explanation:
The given linear expression is (1 – 5q) – (2.5s + 8) – (0.5q + 6)
= 1 – 5q – 2.5s – 8 – 0.5q – 6
= 1 – 5.5q – 2.5s – 14
= -5.5q – 2.5s – 13
Question 27.
YOU BE THE TEACHER
Your friend finds the difference (4m + 9) – (2m – 5). Is your friend correct? Explain your reasoning.
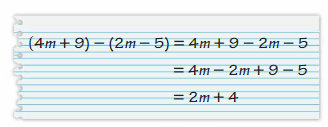
Answer:
Wrong
Explanation:
The given expression is (4m + 9) – (2m – 5)
= 4m + 9 – 2m + 5
= 2m + 14
Question 28.
GEOMETRY
The expression 17n + 11 represents the perimeter of the triangle. What is the length of the third side? Explain your reasoning.
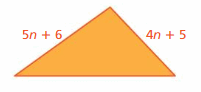
Answer:
The length of the third side is 8n.
Explanation:
Perimeter of the triangle = 17n + 11
5n + 6 + 4n + 5 + third side = 17n + 11
9n + 11 + third side = 17n + 11
third side = 17n + 11 – (9n +11)
= 17n + 11 – 9n – 11
= 8n
The length of the third side is 8n.
Question 29.
LOGIC
Your friend says the sum of two linear expressions is always a linear expression. Is your friend correct? Explain.
Answer:
yes, the sum of two linear expressions is always a linear expression.
Explanation:
The sum of two linear expressions is always a linear expression. But the product of linear expressions may not be the linear expression.
Question 30.
MODELING REAL LIFE
You burn 265 calories running and then 7 calories per minute swimming. Your friend burns 273 calories running and then 11 calories per minute swimming. You each swim for the same number of minutes. Find and interpret the difference in the amounts of calories burned by you and your friend.

Answer:
The difference in the amounts of calories burned by you and your friend is 8 + 4m.
Explanation:
The number of calories your burn by running and swimming is 265 + 7m
The number of calories your friend burns by running and swimming is 273 + 11m
The difference in amount of calories burn = 273 + 11m – (265 + 7m)
= 273 + 11m – 265 – 7m
= 8 + 4m
The difference in the amounts of calories burned by you and your friend is 8 + 4m.
Question 31.
DIG DEEPER!
You start a new job. After w weeks, you have (10w + 120) dollars in your savings account and (45w + 25) dollars in your checking account.
a. What is the total amount of money in the accounts? Explain.
b. How much money did you have before you started your new job? How much money do you save each week?
c. You want to buy a new phone for $150, and still have $500 left in your accounts afterwards. Explain how to determine when you can buy the phone.
Answer:
a. The total amount of money in the accounts = (55w + 145) dollars
b. You started a new job with 120 dollars savings and you earned 10 dollars savings each week.
c. You can buy the phone after 9 weeks of starting new job.
Explanation:
You have (10w + 120) dollars in your savings account and (45w + 25) dollars in your checking account.
a.
The total amount of money in the accounts = 10w + 120 + 45w + 25
= 55w + 145
b.
In the saving’s account the multiple of w is the amount earned during job and other constant is the amount you have before the new job.
So, you started a new job with 120 dollars savings and you earned 10 dollars savings each week.
c.
The total amount in accounts is (55w + 145) dollars
You want to buy a new phone for $150, and still have $500 left in your accounts afterwards
Deduct $150 from total amount so that the remaining amount should be $500.
55w + 145 – 150 = 500
55w – 5 = 500
55w = 500 + 5
55w = 505
w = $505/55
w = 9.1818
So, you can buy the phone after 9 weeks of starting new job.
Question 32.
REASONING
Write an expression in simplest form that represents the vertical distance between the two lines shown. What is the distance when x = 3? when x = -3?
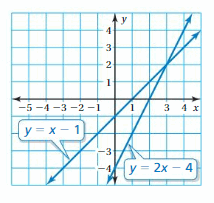
Answer:
The vertical distance between the two lines is 3 units.
Explanation:
Given equations are y = x – 1, y = 2x – 4
Equating those two
x – 1 = 2x – 4
-1 + 4 = 2x – x
3 = x
So, the vertical distance between the two lines is 3 units.
Lesson 3.3 The Distributive Property
EXPLORATION 1
Using Models to Write Expressions
Work with a partner.
a. Write an expression that represents the area of the shaded region in each figure.
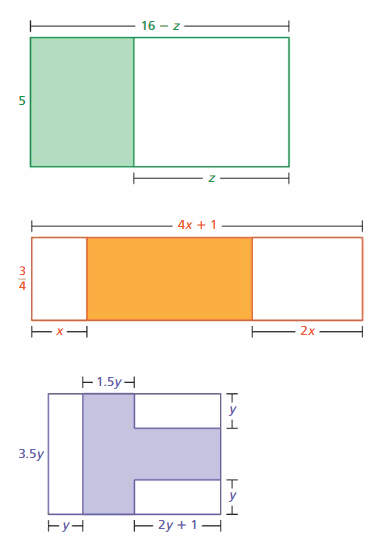

b. Compare your expressions in part(a) with other groups in your class. Did other groups write expressions that look different than yours? If so, determine whether the expressions are equivalent.
3.3 Lesson
Try It
Simplify the expression.
Question 1.
-1(x + 9)
Answer:
-1(x + 9) = 9 – x
Explanation:
Given expression is -1(x + 9)
= -x + 9
Question 2.
![]()
Answer:
2/3 (-3z – 6) = -2z – 4
Explanation:
Given expression is 2/3 (-3z – 6)
= 2/3(-3z) – 2/3(6)
= -2z – 2(2)
= -2z – 4
Question 3.
-1.5(8m – n)
Answer:
-1.5(8m – n) = -12m + 1.5n
Explanation:
Given expression is -1.5(8m – n)
= -1.5(8m) + 1.5(n)
= -12m + 1.5n
Try It
Simplify the expression.
Question 4.
2(-3s + 1 – 5)
Answer:
2(-3s + 1 – 5) = -6s – 8
Explanation:
Given expression is 2(-3s + 1 – 5)
= 2(-3s) + 2(1) + 2(-5)
= -6s + 2 – 10
= -6s – 8
Question 5.
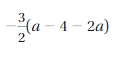
Answer:
-3/2 (a – 4 – 2a) = 3a/2 + 6
Explanation:
Given expression is -3/2 (a – 4 – 2a)
= -3/2 (a) + 3/2(4) + 3/2(2a)
= -3a/2 + 3(2) + 3(a)
= -3a/2 + 6 + 3a
= (-3a + 6a)/2 + 6
= 3a/2 + 6
Try It
Simplify the expression.
Question 6.
3.5m – 1.5(m – 10)
Answer:
3.5m – 1.5(m – 10) = 2m + 15
Explanation:
Given expression is 3.5m – 1.5(m – 10)
= 3.5m – 1.5(m) + 1.5(10)
= 3.5m – 1.5m + 15
= 2m + 15
Question 7.
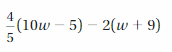
Answer:
4/5(10w – 5) – 2(w + 9) = 6w – 22
Explanation:
Given expression is 4/5(10w – 5) – 2(w + 9)
= 4/5(10w) – 4/5(5) – 2w – 18
= 4(2w) – 4 – 2w – 18
= 8w – 2w – 22
= 6w – 22
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
WRITING
Explain how to use the Distributive Property when simplifying an expression.
Answer:
Distributive property says that a(b+ c) = ab + ac and a(b – c) = ab – ac
So, you need to expand the outer number with the sum or difference inside the braces
And perform the required arithmetical operations to get the simplified expression.
USING THE DISTRIBUTIVE PROPERTY
Simplify the expression.
Question 9.
![]()
Answer:
5/6 (-2y + 3) = -5y/3 + 5/2
Explanation:
Given expression is 5/6 (-2y + 3)
= 5/6(-2y) + 5/6(3)
= -10y/6 + 15/6
= -5y/3 + 5/2
Question 10.
6(3s – 2.5 – 5s)
Answer:
6(3s – 2.5 – 5s) = -15 – 12s
Explanation:
Given expression is 6(3s – 2.5 – 5s)
= 6(-2.5 – 2s)
= 6(-2.5) – 6(2s)
= -15 – 12s
Question 11.
![]()
Answer:
3/10(4m – 8) + 9m = (51m – 12)/5
Explanation:
Given expression is 3/10(4m – 8) + 9m
= 3/10(4m) – 3/10(8) + 9m
= 3/5(2m) – 3/5(4) + 9m
= 6m/5 – 12/5 + 9m
= (6m + 45m)/5 – 12/5
= 51m/5 – 12/5
= (51m – 12)/5
Question 12.
2.25 – 2(7.5 – 4h)
Answer:
2.25 – 2(7.5 – 4h) = 8h – 12.75
Explanation:
Given expression is 2.25 – 2(7.5 – 4h)
= 2.25 – 2(7.5) + 2(4h)
= 2.25 – 15 + 8h
= 8h – 12.75
Question 13.
STRUCTURE

Use the terms at the left to complete the expression below so that it is equivalent to 9x – 12. Justify your answer.

Answer:
3/2 (4x – 8) + 3x
Explanation:
The expression can be
3/2 (4x – 8) + 3x
= 3/2(4(x – 2)) + 3x
= 3(2(x – 2)) + 3x
= 6(x – 2) + 3x
= 6x – 12 + 3x
= 9x – 12
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 14.
A rectangular room is 10 feet longer than it is wide. How many 1-foot square tiles does it take to tile along the inside walls of the room?
Answer:
The number of tiles required is 4w + 20.
Explanation:
Let the width of the rectangular room is w
The length of the rectangular room is w + 10
Perimeter of the rectangular room = 2(length + with)
= 2(w + 10 + w)
= 2(2w +10)
= 4w + 20
So, the number of tiles required is 4w + 20.
Question 15.
How many 2-foot square tiles does it take to tile the border of the pool in Example 4? Explain.
Answer:
(4s + 8) 2 foot square tiles are required.
Explanation:
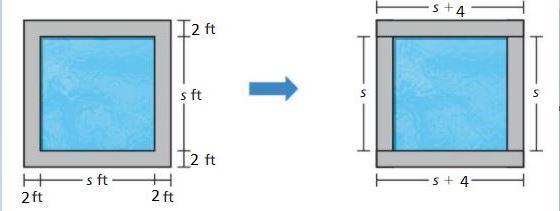
The diagram shows that the tiled border can be divided into two sections that each requires s + 4 tiles and two sections that each requires s tiles. So, the number of tiles can be represented as 2(s + 4) + 2s
2(s + 4) + 2s = 2(s) + 2(4) + 2s
= 4s + 8
So, (4s + 8) 2 foot square tiles are required.
The Distributive Property Homework & Practice 3.3
Review & Refresh
Find the sum or difference.
Question 1.
(5b – 9) + (b + 8)
Answer:
(5b – 9) + (b + 8) = 6b – 1
Explanation:
Given expression is (5b – 9) + (b + 8)
= 5b – 9 + b + 8
= 6b – 1
Question 2.
(3m + 5) – (6 – 5m)
Answer:
(3m + 5) – (6 – 5m) = 8m – 1
Explanation:
Given expression is (3m + 5) – (6 – 5m)
= 3m + 5 – 6 + 5m
= 8m – 1
Question 3.
(1 – 9z) + 3(z – 2)
Answer:
(1 – 9z) + 3(z – 2) = -5 – 6z
Explanation:
Given expression is (1 – 9z) + 3(z – 2)
= 1 – 9z + 3(z) – 3(2)
= 1 – 9z + 3z – 6
= -5 – 6z
Question 4.
(7g – 6) – (-3n – 4)
Answer:
(7g – 6) – (-3n – 4) = 7g + 3n – 2
Explanation:
Given expression is (7g – 6) – (-3n – 4)
= 7g – 6 -(-3n) -(-4)
= 7g – 6 + 3n + 4
= 7g + 3n – 2
Evaluate the expression.
Question 5.
-62
Answer:
-6² = -36
Explanation:
Given expression is -62
-6 x 6 = -36
Question 6.
-92 . 3
Answer:
-9² . 3 = -243
Explanation:
Given expression is -9² . 3
= -9 . 9 . 3
= -9 . 27
= -243
Question 7.
(-7) . (-2) . (-4)
Answer:
(-7) . (-2) . (-4) = -56
Explanation:
Given expression is (-7) . (-2) . (-4)
= -7 . -2 . -4
= 14 . -4
= -56
Copy and complete the statement using <, >, or =.
Question 8.
![]()
Answer:
11 = | -11 |
Explanation:
11 = | -11 |
mod of -11 is positive 11
So, they are equal.
Question 9.
![]()
Answer:
| 3.5 | < | -5.8 |
Explanation:
| 3.5 | _ | -5.8 |
3.5 < 5.8
Question 10.
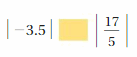
Answer:
| -3.5 | < | 17/5 |
Explanation:
| -3.5 | _ | 17/5 |
3.5 < 3.4
Concepts, Skills, & Problem Solving
USING MODELS
Write two different expressions that represent the area of the shaded region. Show that the expressions are equivalent. (See Exploration 1, p. 103.)
Question 11.
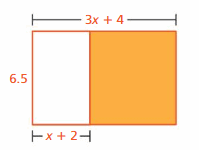
Answer:
6.5(2x + 2), 13x + 13
Explanation:
The length of the shaded region is 6.5
The width of the shaded region is (3x + 4) – (x + 2) = 3x + 4 – x – 2
= 2x + 2
The area of the shaded region = length . width
= 6.5 . (2x + 2)
= 6.5(2x + 2)
= 6.5(2x) + 6.5(2)
= 13x + 13
The second way is as follows
The length of bigger rectangle is 3x + 4
Width of the bigger rectangle is 6.5
Area of the bigger rectangle = length . width
= 6.5(3x + 4)
The length of unshaded region is x + 2
width of the unshaded region is 6.2
Area of the unshaded region = length . width
= 6.5(x + 2)
Area of the shaded region = Area of the bigger rectangle – area of the shaded region
= 6.5(3x + 4) – 6.5(x + 2)
= 6.5(3x + 4 -(x + 2))
= 6.5(3x + 4 – x – 2)
= 6.5(2x + 2)
= 6.5(2x) + 6.5(2)
= 13x + 13
Question 12.
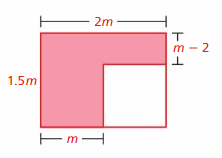
Answer:
2.5m² – 2m, 1.5m² + m(m – 2)
Explanation:
The first way is here.
The length of the bigger rectangle is 1.5m
The width of the bigger rectangle is 2m
The area of the bigger rectangle = length . width
= 1.5m x 2m = 3m²
Length of the unshaded region is 1.5m – (m – 2) = 1.5m – m + 2
= 0.5m + 2
Width of the unshaded region = 2m – m = m
Area of the unshaded region = length . width
= (0.5m + 2) . m
Area of the shaded region = The area of the bigger rectangle – Area of the unshaded region
= 3m² – m(0.5m + 2)
= 3m² – 0.5m² -2m
= 2.5m² – 2m
The second way is as follows
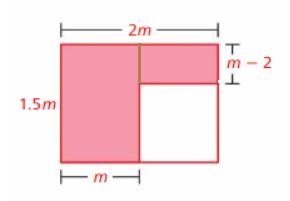
The length of the first shaded rectangle = 1.5m
The width of the first shaded rectangle = m
Area of the first shaded rectangle = length . width
= 1.5m x m
= 1.5m²
The length of the second shaded rectangle = m – 2
The width of the first shaded rectangle = 2m – m = m
Area of the second shaded rectangle = length . width
= m(m – 2)
Therefore, area of the shaded region = Area of the first shaded rectangle + Area of the second shaded rectangle
= 1.5m² + m(m – 2)
= 1.5m² + m² – 2m
= 2.5m² – 2m
Therefore, two expressions that represent the area of the shaded region is 2.5m² – 2m, 1.5m² + m(m – 2).
USING THE DISTRIBUTIVE PROPERTY
Simplify the expression.
Question 13.
3(a – 7)
Answer:
3(a – 7) = 3a – 21
Explanation:
The given expression is 3(a – 7)
= 3(a) – 3(7)
= 3a – 21
Question 14.
-6(2 + x)
Answer:
-6(2 + x) = -12 – 6x
Explanation:
The given expression is -6(2 + x)
= -6(2) +(-6)(x)
= -12 -6(x)
= -12 – 6x
Question 15.
-5(3m – 4)
Answer:
-5(3m – 4) = -15m + 20
Explanation:
The given expression is -5(3m – 4)
= -5(3m) – (-5) (4)
= -15m +5(4)
= -15m + 20
Question 16.
-9(-5 – 4c)
Answer:
-9(-5 – 4c) = 45 + 36c
Explanation:
The given expression is -9(-5 – 4c)
= -9(-5) – (-9) (4c)
= 45 + 9(4c)
= 45 + 36c
Question 17.
4.5 (3s + 6)
Answer:
4.5 (3s + 6) = 13.5s+ 27
Explanation:
The given expression is 4.5 (3s + 6)
= 4.5(3s) + 4.5(6)
= 13.5s+ 27
Question 18.
-1.4 (-5 + 7g)
Answer:
-1.4 (-5 + 7g) = 7 – 9.8g
Explanation:
The given expression is -1.4 (-5 + 7g)
= -1.4(-5) -1.4(7g)
= 7 – 9.8g
Question 19.
![]()
Answer:
2/5(6 – 5p) = 12/5 – 2p
Explanation:
The given expression is 2/5(6 – 5p)
= 2/5(6) – 2/5(5p)
= 12/5 – 2p
Question 20.
![]()
Answer:
-4/3 (3q – 10) = -4q + 40/3
Explanation:
The given expression is -4/3 (3q – 10)
= -4/3 (3q) + 4/3(10)
= -4q + 40/3
Question 21.
2(3 + 4y + 5)
Answer:
2(3 + 4y + 5) = 16 + 8y
Explanation:
The given expression is 2(3 + 4y + 5)
= 2(8 + 4y)
= 2(8) + 2(4y)
= 16 + 8y
Question 22.
-9(8 + 6n – 4)
Answer:
-9(8 + 6n – 4) = -36 – 54n
Explanation:
The given expression is -9(8 + 6n – 4)
= -9(4 + 6n)
= -9(4) – 9(6n)
= -36 – 54n
Question 23.
-6(-4d – 8.3 + 3d)
Answer:
-6(-4d – 8.3 + 3d) = 6d + 49.8
Explanation:
The given expression is -6(-4d – 8.3 + 3d)
= -6(-d – 8.3)
= -6(-d) + 6(8.3)
= 6d + 49.8
Question 24.
2.3h(6 – k)
Answer:
2.3h(6 – k) = 13.8h – 2.3hk
Explanation:
The given expression is 2.3h(6 – k)
= 2.3h(6) – 2.3h(k)
= 13.8h – 2.3hk
Question 25.
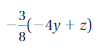
Answer:
-3/8 (-4y + z) = 3y/2 – 3z/8
Explanation:
The given expression is -3/8 (-4y + z)
= -3/8 (-4y) – 3/8(z)
= 3y/2 – 3z/8
Question 26.
2(-2w – 1.2 + 7x)
Answer:
2(-2w – 1.2 + 7x) = -4w- 2.4 + 14x
Explanation:
The given expression is 2(-2w – 1.2 + 7x)
= 2(-2w) + 2(-1.2) + 2(7x)
= -4w- 2.4 + 14x
Question 27.
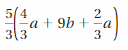
Answer:
5/3(4/3 a + 9b + 2/3 a) = 10a/3 + 15b
Explanation:
The given expression is 5/3(4/3 a + 9b + 2/3 a)
= 5/3 ( 6a/3 + 9b)
= 5/3 (2a + 9b)
= 5/3 (2a) + 5/3 (9b)
= 10a/3 + 5 (3b)
= 10a/3 + 15b
YOU BE THE TEACHER
Your friend simplifies the expression. Is your friend correct? Explain your reasoning
Question 28.
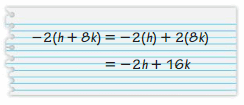
Answer:
Wrong.
Explanation:
-2(h + 8k) = -2(h) -2(8k)
= -2h – 16k
Question 29.

Answer:
Wrong
Explanation:
-3(4 – 5b + 7) = -3(11 – 5b)
= -3(11) -3(-5b)
= -33 + 15b
SIMPLIFYING EXPRESSIONS
Simplify the expression.
Question 30.
-3(5g + 1) + 8g
Answer:
-3(5g + 1) + 8g = -7g – 3
Explanation:
The given expression is -3(5g + 1) + 8g
= -3(5g) -3(1) + 8g
= -15g – 3 + 8g
= -7g – 3
Question 31.
-6a + 7(-2a – 4)
Answer:
-6a + 7(-2a – 4) = -20a – 28
Explanation:
The given expression is -6a + 7(-2a – 4)
= -6a + 7(-2a) +7(-4)
= -6a – 14a – 28
= -20a – 28
Question 32.
9 – 3(5 – 4x)
Answer:
9 – 3(5 – 4x) = -6 + 12x
Explanation:
The given expression is 9 – 3(5 – 4x)
= 9 – 3(5) -3(-4x)
= 9 – 15 + 12x
= -6 + 12x
Question 33.
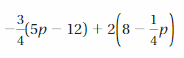
Answer:
-3/4(5p – 12) + 2(8 – 1/4 p) = -17p/4 + 25
Explanation:
The given expression is -3/4(5p – 12) + 2(8 – 1/4 p)
= -3/4 (5p) -3/4(-12) + 2(8) + 2(-1/4p)
= -15p/4 + 9 + 16 – p/2
= (-15p -2p)/4 + 25
= -17p/4 + 25
Question 34.
c(4 + 3c) – 0.75(c + 3)
Answer:
c(4 + 3c) – 0.75(c + 3) = 4c + 3c² – 0.75c – 2.25
Explanation:
The given expression is c(4 + 3c) – 0.75(c + 3)
= c(4) + c(3c) – 0.75(c) – 0.75(3)
= 4c + 3c² – 0.75c – 2.25
Question 35.
![]()
Answer:
-1 – 2/3(6/7 – 3/7 n) = -33/21 + 6n/21
Explanation:
The given expression is -1 – 2/3(6/7 – 3/7 n)
= -1 -2/3(6/7) – 2/3(-3/7 n)
= -1 – 12/21 + 6n/21
= (-21 – 12)/21 + 6n/21
= -33/21 + 6n/21
Question 36.
MODELING REAL LIFE
The cost (in dollars) of a custom-made sweatshirt is represented by 3.5n + 29.99, where n is the number of different colors in the design. Write and interpret a simplified expression that represents the cost of 15 sweatshirts.
Answer:
The cost of 15 sweatshirts is 52.5n + 449.85
Explanation:
The cost (in dollars) of a custom-made sweatshirt is represented by 3.5n + 29.99
To find the cost of 15 sweatshirts, we need to multiply the expression by 15
= 15(3.5n + 29.99)
= 15(3.5n) + 15(29.99)
= 52.5n + 449.85
Therefore, the cost of 15 sweatshirts is 52.5n + 449.85
Question 37.
MODELING REAL LIFE
A ski resort makes snow using a snow fan that costs $1200. The fan has an average daily operation cost of $9.50. Write and interpret a simplified expression that represents the cost to purchase and operate 6 snow fans.

Answer:
The expression that represents the cost to purchase and operate 6 snow fans is 7200 + 57d.
Explanation:
Given that,
A ski resort makes snow fan that costs $1200
The fan has an average daily operation cost of $ 9.50
We have to write a simplified expression that represents the cost to purchase and operate 6 snow fans.
And variable d represents the number of days that the resort operates the fans.
Now, cost of 6 snow fans = 6 x cost of each snow fan = 6 x 1200 = 7200
The cost to operate 6 fans = 6 x number of days x cost to operate each fan
= 6 x d x 9.5 = 57d
So, the expression for total cost will be cost of fans + cost to operate = 7200 + 57d.
Question 38.
NUMBER SENSE
Predict whether the instructions below will produce equivalent expressions. Then show whether your prediction is correct.
- Subtract 3 from n, add 3 to the result, and then triple that expression.
- Subtract 3 from n, triple the result, and then add 3 to that expression.
Answer:
Your prediction is wrong.
Explanation:
a. Subtract 3 from n = n – 3
Add 3 to the result = n – 3 + 3 = n
And then triple that expression = n x n x n = n³.
b. Subtract 3 from n = n – 3
Triple the result = (n – 3) . (n – 3) . (n – 3) = (n – 3)³
And then add 3 to that expression = (n – 3)³ + 3
Therefore, n³ is not equivalent to (n – 3)³ + 3
Hence, the prection is wrong.
USING A MODEL
Draw a diagram that shows how the expression can represent the area of a figure. Then simplify the expression.
Question 39.
5(2 + x + 3)
Answer:
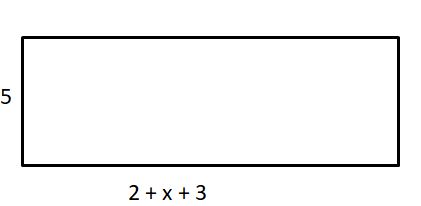
Explanation:
The area of rectangle = length . width
= 5(2 + x + 3)
= 5(5 + x)
= 5(5) + 5(x)
= 25 + 5x
Therefore, area is (25 + 5x)
Question 40.
(4 + 1)(x + 2x)
Answer:
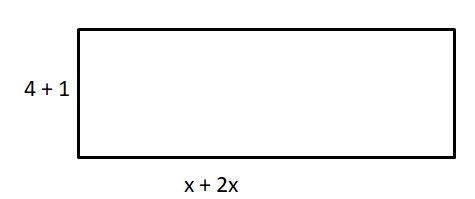
Explanation:
Length = 4 + 1
width = x + 2x
The area of rectangle = length . width
= (4 + 1) . (x + 2x)
= 5 . (3x)
= 15x
Therefore, area is 15x.
Question 41.
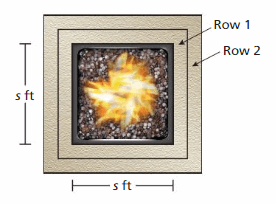
DIG DEEPER!
A square firepit with a side length of s feet is bordered by 1-foot square stones as shown.
a. How many stones does it take to border the firepit with two rows of stones? Use a diagram to justify your answer.
b. You border the fire pit with rows of stones. How many stones are in the nth row? Explain your reasoning.
Answer:
a. 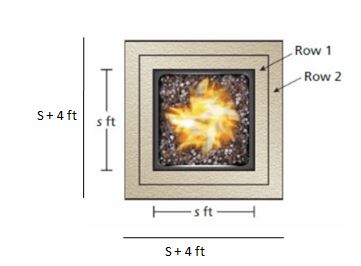
The number of stones = (s + 2)² + (s + 4)²
b. The area of the nth row square is (s + 2n)² ft².
Explanation:
a. The side length of the inner sqaure is s
The area of the sqaure = side²
= s²
The side length of the 1st row square is s + 1 + 1 = s + 2 ft
The area of the 1st row square = side²
= (s + 2)² ft²
The side length of the 2nd row of the sqaure is s + 2 + 2 = s + 4 ft
The area of the 2st row square = side²
= (s + 4)² ft²
So, the number of stones = (s + 2)² + (s + 4)²
b.
The side length of the nth row is s + 2n ft
The area of the nth row square = side²
= (s + 2n)² ft²
Question 42.
PUZZLE
Your friend asks you to perform the following steps.
- Pick any number except 0.
- Add 2 to your number.
- Multiply the result by 3.
- Subtract 6 from the result.
- Divide the result by your original number.
Your friend says, “The final result is 3!” Is your friend correct? If so, explain how your friend knew the final result. If not, explain why not.
Answer:
Yes, my friend is correct.
Explanation:
- Pick any number except 0.
I have taken 2. - Add 2 to your number.
2 + 2 = 4 - Multiply the result by 3.
4 x 3 = 12 - Subtract 6 from the result.
12 – 6 = 6 - Divide the result by your original number.
6/2 = 3
Lesson 3.4 Factoring Expressions
Factoring Expressions
EXPLORATION 1
Finding Dimensions
Work with a partner.
a. The models show the areas (in square units) of parts of rectangles.
Use the models to find the missing values that complete the expressions. Explain your reasoning.?

b. Are the expressions you wrote in part(a) equivalent to the original expressions? Explain your reasoning.
c. Explain how you can use the Distributive Property to find rational number factors of an expression.
Try It
Factor the expression using the GCF.
Question 1.
15x + 25
Answer:
15x + 25 = 5(3x + 5)
Explanation:
Find the G.C.F of 15x and 25
15x = 3 . 5 . x
25 = 5. 5
The common prime factor is 5.
So, the GCF of 15x and 25 is 5
Use the GCF to factor the expression
15x + 25 = 5(3x) + 5(5)
= 5(3x + 5)
Question 2.
4y – 20
Answer:
4y – 20 = 4(y – 5)
Explanation:
Find the G.C.F of 4y and 20
15x = 2 . 2 . y
20 = 2 . 2 . 5
The common prime factors are 2 . 2 = 4
So, the GCF of 4y and 20 is 4
Use the GCF to factor the expression
4y – 20 = 4(y) – 4(5)
= 4(y – 5)
Question 3.
36c + 24d
Answer:
36c + 24d = 12(3c + 2d)
Explanation:
The G.C.F of 36c, 24d is
36c = 2 . 2 . 3 . 3 . c
24d = 2 . 3 . 2 . 2 . d
The common prime factors are 2 . 2 . 3 = 12
The G.C.F of 36c, 24d is 12
Use the GCF to factor the expression
36c + 24d = 12(3c) + 12(2d)
= 12(3c + 2d)
Try It
Factor out the coefficient of the variable term.
Question 4.
![]()
Answer:
½n – ½ = ½(n – 1)
Explanation:
Given that,
½n – ½
½n = ½ . n
½ = ½ . 1
Use the distributive property to factor out ½.
½n – ½ = ½(n) – ½(1)
= ½(n – 1)
Question 5.
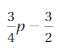
Answer:
3/4 p – 3/2 = 3/2(p/2 – 1)
Explanation:
Given that,
3/4 p – 3/2
3/2 = 3/2 . 1
3/4 p = 3/2 . 1/2 . p
Use the distributive property to factor out 3/2
3/4 p – 3/2 = 3/2(1/2 p) – 3/2(1)
= 3/2(p/2 – 1)
Question 6.
5 + 2.5q
Answer:
5 + 2.5q = 2.5(2 + q)
Explanation:
Given that,
5 + 2.5q
5 = 2.5 . 2
2.5 = 2.5 . 1
Use the distributive property to factor out 2.5
5 + 2.5q = 2.5(2) + 2.5(q)
= 2.5(2 + q)
Try It
Question 7.
Factor -5 out of -5d + 30.
Answer:
-5d + 30 = -5(d – 6)
Explanation:
Given that,
-5d + 30.
-5d = -5 . d
30 = 5 . 6 = -5 . -6
-5d + 30 = -5(d) – 5(-6)
= -5(d – 6)
Question 8.
Factor -4 out of -8k – 12.
Answer:
-8k – 12 = -4(2k + 3)
Explanation:
given that,
-8k – 12
-8k = -2 . 4 . k
-12 = -4 . 3
The G.C.f of -8k, -12 is -4.
-8k – 12 = -4(2k) – 4(3)
= -4(2k + 3)
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FACTORING OUT THE GCF
Factor the expression using the GCF.
Question 9.
16n – 24
Answer:
16n – 24 = 8(2n – 3)
Explanation:
Find the G.C.F of 16n, 24
16n = 2 . 2 . 2 . 2 . n
24 = 2 . 2 . 2 . 3
The G.C.F of 16n, 24 is 2 . 2 . 2 = 8
Use the GCF to factor the expression
16n – 24 = 8(2n)- 8(3)
= 8(2n – 3)
Question 10.
42a + 14b
Answer:
42a + 14b = 14(3a + b)
Explanation:
Find the G.C.F of 42a, 14b
42a = 2 . 3 . 7 . a
14b = 2 . 7 . b
The greatest common factor of 42a, 14b is 2 . 7 = 14
Use the GCF to factor the expression
42a + 14b = 14(3a) + 14(b)
= 14(3a + b)
FACTORING OUT A RATIONAL NUMBER
Factor out the coefficient of the variable term.
Question 11.
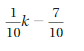
Answer:
1/10 k – 7/10 = 1/10(k – 7)
Explanation:
Given that,
1/10 k – 7/10
The factors of 1/10, 7/10 are
1/10 = 1/10 . 1
7/10 = 7 . 1/10
Use the distributive property to factor out 1/10
1/10 k – 7/10 = 1/10 (k) – 1/10(7)
= 1/10(k – 7)
Question 12.
42 + 3.5h
Answer:
42 + 3.5h = 3.5(12 + h)
Explanation:
Find the factors of 42, 3.5
42 = 4 . 3 . 3.5
3.5 = 3.5 . 1
Use the distributive property to factor out 3.5
42 + 3.5h = 3.5(12) + 3.5(h)
= 3.5(12 + h)
FACTORING OUT A NEGATIVE NUMBER
Factor out the indicated number.
Question 13.
Factor -8 out of -3d + 56.
Answer:
-3d + 56 = -8(3d/8 – 7)
Explanation:
Get the factors of -3d, 56
-3d = 3d/8 . -8
56 = -7 . -8
Use the distributive property to factor out -8
-3d + 56 = -8(3d/8) – 8(-7)
= -8(3d/8 – 7)
Question 14.
Factor -12 out of -24k + 120.
Answer:
-24k + 120 = -12(2k – 10)
Explanation:
Get the factors of -24k, 120
-24k = -12. 2. k
120 = -12. -10
Use the distributive property to factor out -12
-24k + 120 = -12(2k) -12(-10)
= -12(2k – 10)
Question 15.
WRITING
Describe the relationship between using the Distributive Property to simplify an expression and to factor an expression. Give an example to justify your answer.
Answer:
The distributive property tells that a(b – c) = ab – ac and a(b + c) = ab + ac. It means you can seperate the common term and represent it as the factor.
Explanation:
The relationship between using the Distributive Property to simplify an expression and to factor an expression is mentioned here.
The distributive property tells that a(b – c) = ab – ac and a(b + c) = ab + ac. It means you can seperate the common term and represent it as the factor.
Let us take one example question 12x + 40y
The factors of 12x = 3 . 4 . x, the factors of 40y = 5 . 2 . 4 . y
The common factor is 4. So, take out the common factor and use the distribuyive property.
12x + 4y = 4(3x) + 4(10y)
= 4(3x + 10y)
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 16.
An organization drills 3 wells to provide access to clean drinking water. The cost (in dollars) to drill and maintain the wells for n years is represented by 34,500 + 540n. Write and interpret an expression that represents the cost to drill and maintain one well for n years.

Answer:
The cost to drill and maintain one well for n years is 10(1150 + 18n).
Explanation:
The cost to drill and maintain 3 wells for n years is 34,500 + 540n
To get the drill and maintainance cost for 1 well, you need to find the factors
34500 = 10 . 10 . 3 . 5 . 23
540n = 3. 9 . 2 . 10 . n
The G.C.F of 34500 and 540n is 10 . 3 = 30
34,500 + 540n = 30(1150) + 30(18n)
= 30(1150 + 18n)
Divide the expression by 3 to get the drill and maintainance cost for 1 well
= 30(1150 + 18n)/ 3 = 10(1150 + 18n)
So, the cost to drill and maintain one well for n years is 10(1150 + 18n)
Question 17.
A photograph is 16 inches long and has an area of (16x + 96) square inches. A custom-made frame is 2 inches wide and costs $0.50 per square inch. Write an expression that represents the cost of the frame.

Answer:
The cost of frame is $0.50(4x + 104)
Explanation:
Given that,
Length of photograph = 16 inches
Area of photograph = (16x + 96) sq inches
Factor out 16 from the expression
= 16(x) + 16(6) = 16(x + 6)
So, the width of the photograph is x + 6 inches
A custom-made frame is 2 inches wide and costs $0.50 per square inch.
The length of frame and photograph is 16 + 2 + 2 = 20 inches
The bredth of the frame & photograph is (x + 6 + 4) = x + 10 inches
Area of the photograph and frame = length . width
= 20(x + 10)
The area of frame = The area of photograph and frame – Area of photograph
= 20(x + 10) – (16x + 96)
= 20x + 200 – 16x – 96
= 4x + 104 sq inches
The cost of frame is $0.50 per square inch
So, the cost of the frame is 0.50(4x + 104).
Factoring Expressions Homework & Practice 3.4
Review & Refresh
Simplify the expression.
Question 1.
8(k – 5)
Answer:
8(k – 5) = 8k – 40
Explanation:
The given expression is 8(k – 5)
= 8(k) – 8(5)
= 8k – 40
Question 2.
-4.5(-6 + 2d)
Answer:
-4.5(-6 + 2d) = 27 – 9d
Explanation:
The given expression is -4.5(-6 + 2d)
= -4.5(-6) – 4.5(2d)
= 27 – 9d
Question 3.
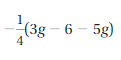
Answer:
-1/4 (3g – 6 – 5g) = 3/2 + g/2
Explanation:
The given expression is -1/4 (3g – 6 – 5g)
= -1/4(-6 – 2g)
= -1/4(-6) – 1/4(-2g)
= 3/2 + 1/2 g
Find the difference. Write fractions in simplest form.
Question 4.
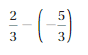
Answer:
2/3 – (-5/3) = 7/3
Explanation:
Given that,
2/3 – (-5/3) = 2/3 + 5/3
= (2 + 5)/3 = 7/3
Question 5.
-4.7 – 5.6
Answer:
-4.7 – 5.6 = -10.3
Explanation:
Given that,
-4.7 – 5.6 = -10.3
Question 6.
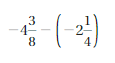
Answer:
-4(3/8) – (-2(1/4) = -17/8
Explanation:
Given that,
-4(3/8) – (-2(1/4) = -35/8 – (-9/4)
= -35/8 + 9/4 = (-35 + 18)/8
= -17/8
Evaluate the expression when x = 4, y = -6, and z = -3.
Question 7.
y ÷ z
Answer:
y ÷ z = 2
Explanation:
Given expression is y ÷ z
Put y = -6, and z = -3
y ÷ z = -6 ÷ -3
= 6 ÷ 3 = 2
Question 8.
\(\frac{4 y}{2 x}\)
Answer:
4y/2x = -3
Explanation:
Given expression is 4y/2x
Put x = 4, y = -6
4y/2x =(4 x -6)/ (2 x 4)
= -24/8 = -3
Question 9.
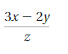
Answer:
(3x – 2y)/z = -8
Explanation:
Given expression is (3x – 2y)/z
Put x = 4, y = -6, and z = -3
= (3 x 4 – 2(-6))/-3
= (12 + 12)/-3
= 24/-3
= -24/3
= -8
Concepts, Skills, & Problem Solving
FINDING DIMENSIONS
The model shows the area (in square units) of each part of a rectangle. Use the model to find the missing values that complete the expression. Explain your reasoning. (See Exploration 1, p. 109.)
Question 10.
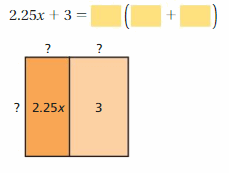
Answer:
2.25x + 3 = 1.5(1.5x + 2)
Explanation:
Find the factors of 2.25x, 3
2.25x = 1.5 . 1.5 . x
3 = 1.5 . 2
So, 2.25x + 3 = 1.5(1.5x) +1.5(2)
= 1.5(1.5x + 2)
Question 11.
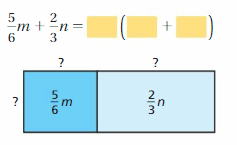
Answer:
5/6 m + 2/3 n = 1/3(5m/2 + 2n)
Explanation:
Find the factors of 5m/6, 2n/3
5m/6 = 1/3 . 5/2 . m
2n/3 = 1/3 . 2 . n
So, 5/6 m + 2/3 n = 1/3(5m/2) + 1/3(2n)
= 1/3(5m/2 + 2n)
FACTORING OUT THE GCF
Factor the expression using the GCF.
Question 12.
9b + 21
Answer:
9b + 21 = 3(3b + 7)
Explanation:
The given expression is 9b + 21
Find the factors of 9b, 21
9b = 3 . 3 . b
21= 7 . 3
G.C.F of 9b, 21 is 3
Use the GCF to factor the expression
9b + 21 = 3(3b) + 3(7)
= 3(3b + 7)
Question 13.
32z – 48
Answer:
32z – 48 = 16(2z – 3)
Explanation:
The given expression is 32z – 48
Find the factors of 32z, -48
32z = 2 . 2 . 2 . 2 . 2 . z
48 = 2 . 2 . 2 . 2 . 3
G.C.F of 32z, -48 is 2 . 2 . 2 . 2 = 16
Use the GCF to factor the expression
32z – 48 = 16(2z) – 16(3)
= 16(2z – 3)
Question 14.
8x + 2
Answer:
8x + 2 = 2(4x + 1)
Explanation:
The given expression is 8x + 2
find the factors of 8x, 2
8x = 2 . 2 . 2 . x
2 = 2. 1
G.C.F of 8x, 2 is 2
Use the GCF to factor the expression
8x + 2 = 2(4x) + 2(1)
= 2(4x + 1)
Question 15.
3y – 24
Answer:
3y – 24 = 3(y – 4)
Explanation:
The given expression is 3y – 24
Find the factors of 3y, 24
3y = 3 . y
24 = 4 . 3
G.C.F of 3y, 24 is 3
Use the GCF to factor the expression
3y – 24 = 3(y) – 3(4)
= 3(y – 4)
Question 16.
14p – 28
Answer:
14p – 28 = 14(p – 2)
Explanation:
The given expression is 14p – 28
Find the factors of 14p, 28
14p = 7 . 2 . p
28 = 7 . 2 . 2
G.C.F of 14p, 28 is 14
Use the GCF to factor the expression
14p – 28 = 14(p) – 14(2)
= 14(p – 2)
Question 17.
6 + 16k
Answer:
6 + 16k = 2(3 + 8k)
Explanation:
The given expression is 6 + 16k
Find the factors of 6, 16k
6 = 2 . 3
16k = 2 . 2 . 2 . 2 . k
G.C.F of 6, 16k is 2
Use the GCF to factor the expression
6 + 16k = 2(3) + 2(8k)
= 2(3 + 8k)
Question 18.
21 – 14d
Answer:
21 – 14d = 7(3 – 2d)
Explanation:
The given expression is 21 – 14d
Get the factors of 21, 14d
21 = 7 . 3
14d = 7 . 2 . d
G.C.F of 21, 14d is 7
Use the GCF to factor the expression
21 – 14d = 7(3) – 7(2d)
= 7(3 – 2d)
Question 19.
20z – 8
Answer:
20z – 8 = 4(5z – 2)
Explanation:
The given expression is 20z – 8
Get the factors of 20z, 8
20z = 5 . 2 . 2 . z
8 = 2 . 2 . 2
G.C.F of 20z, 8 is 4
Use the GCF to factor the expression
20z – 8 = 4(5z) – 4(2)
= 4(5z – 2)
Question 20.
15w + 65
Answer:
15w + 65 = 5(3w + 13)
Explanation:
The given expression is 15w + 65
Get the factors of 15w, 65
15w = 5 . 3 . w
65 = 5 . 13
G.C.F of 15w, 65 is 5
Use the GCF to factor the expression
15w + 65 = 5(3w) + 5(13)
= 5(3w + 13)
Question 21.
36a + 16b
Answer:
36a + 16b = 4(9a + 4b)
Explanation:
The given expression is 36a + 16b
Get the factors of 36a, 16b
36a = 3 . 2 . 3 . 2 . a
16b = 2 . 2 . 2 . 2 . b
G.C.F of 36a, 16b is 4
Use the GCF to factor the expression
36a + 16b = 4(9a) + 4(4b)
= 4(9a + 4b)
Question 22.
21m – 49n
Answer:
21m – 49n = 7(3m + 7n)
Explanation:
The given expression is 21m – 49n
Get the factors of 21m, 49n
21m = 7 . 3 . m
49n = 7 . 7 . n
G.C.F of 21m, 49n
Use the GCF to factor the expression
21m – 49n = 7(3m) + 7(7n)
= 7(3m + 7n)
Question 23.
12 + 9g – 30h
Answer:
12 + 9g – 30h = 3(4 + 3g – 10h)
Explanation:
The given expression is 12 + 9g – 30h
Get the factors of 12, 9g, 30h
12 = 3 . 2 . 2
9g = 3 . 3 . g
30h = 3 . 5 . 2 . h
G.C.F of 12, 9g, 30h is 3
Use the GCF to factor the expression
12 + 9g – 30h = 3(4) + 3(3g) – 3(10h)
= 3(4 + 3g – 10h)
FACTORING OUT A RATIONAL NUMBER
Factor out the coefficient of the variable term.
Question 24.
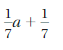
Answer:
1/7 a + 1/7 = 1/7 (a + 1)
Explanation:
The given expression is 1/7 a + 1/7
1/7a = 1/7 . a
1/7 = 1/7 . 1
Use the distributive property to factor out 1/7
1/7 a + 1/7 = 1/7(a) + 1/7(1)
= 1/7 (a + 1)
Question 25.
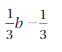
Answer:
1/3 b – 1/3 = 1/3(b – 1)
Explanation:
The given expression is 1/3 b – 1/3
1/3b = 1/3 . b
1/3 = 1/3 . 1
Use the distributive property to factor out 1/3
1/3 b – 1/3 = 1/3(b) – 1/3(1)
= 1/3(b – 1)
Question 26.
![]()
Answer:
3/8 d + 3/4 = 3/4(d/2 + 1)
Explanation:
The given expression is 3/8 d + 3/4
3/8 d = 3/4 . 1/2 . d
3/4 = 3/4 . 1
Use the distributive property to factor out 3/4
3/8 d + 3/4 = 3/4 (d/2) + 3/4(1)
= 3/4(d/2 + 1)
Question 27.
2.2x + 4.4
Answer:
2.2x + 4.4 = 2.2(x +2)
Explanation:
The given expression is 2.2x + 4.4
2.2x = 1.1 . 2 . x
4.4 = 1.1 . 2 . 2
Use the distributive property to factor out 2.2
2.2x + 4.4 = 2.2(x) + 2.2(2)
= 2.2(x +2)
Question 28.
1.5y – 6 = 1.5(y – 4)
Answer:
1.5y – 6
Explanation:
The given expression is 1.5y – 6
1.5y = 1.5 . y
6 = 1.5 . 2 . 2
Use the distributive property to factor out 1.5
1.5y – 6 = 1.5(y) – 1.5(4)
= 1.5(y – 4)
Question 29.
0.8w + 3.6
Answer:
0.8w + 3.6 = 0.8(w + 4.5)
Explanation:
The given expression is 0.8w + 3.6
0.8w = 0.8 . w
3.6 = 0.8 . 4.5
Use the distributive property to factor out 0.8
0.8w + 3.6 = 0.8(w) + 0.8(4.5)
= 0.8(w + 4.5)
Question 30.
Answer:
15/4 + 3/8 x = 3/4(5 + x/2)
Explanation:
The given expression is 15/4 + 3/8 x
15/4 = 3/4 . 5
3/8x = 3/4 . 1/2 . x
Use the distributive property to factor out 3/4
15/4 + 3/8 x = 3/4(5) + 3/4(x/2)
= 3/4(5 + x/2)
Question 31.
4h – 3
Answer:
4h – 3 = 2(2h – 1.5)
Explanation:
The given expression is 4h – 3
4h = 2 . 2 h
3 = 2 . 1.5
Use the distributive property to factor out 2
4h – 3 = 2(2h) – 2(1.5)
= 2(2h – 1.5)
Question 32.
0.15c – 0.072
Answer:
0.15c – 0.072 = 0.03(5c – 2.4)
Explanation:
The given expression is 0.15c – 0.072
0.15c = 0.03 . 5 . c
0.072 = 0.03 . 2.4
Use the distributive property to factor out 0.03
0.15c – 0.072 = 0.03(5c) – 0.03(2.4)
= 0.03(5c – 2.4)
Question 33.
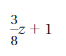
Answer:
3/8 z + 1 = 1/8(3z + 8)
Explanation:
The given expression is 3/8 z + 1
3/8 z = 1/8 . 3 . z
1 = 1/8 . 8
Use the distributive property to factor out 1/8
3/8 z + 1 = 1/8(3z) + 1/8(8)
= 1/8(3z + 8)
Question 34.
Answer:
6s – 3/4 = 3(2s – 1/4)
Explanation:
The given expression is 6s – 3/4
6s = 3 . 2 . s
3/4 = 3 . 1/4
Use the distributive property to factor out 3
6s – 3/4 = 3(2s) – 3(1/4)
= 3(2s – 1/4)
Question 35.
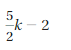
Answer:
5/2 k – 2 = 1/2(5k – 4)
Explanation:
The given expression is 5/2 k – 2
5/2k = 1/2 . 5 . k
2 = 1/2 . 4
Use the distributive property to factor out 1/2
5/2 k – 2 = 1/2 (5k) – 1/2(4)
= 1/2(5k – 4)
YOU BE THE TEACHER
Your friend factors the expression. Is your friend correct? Explain your reasoning.
Question 36.
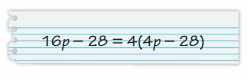
Answer:
Wrong
Explanation:
Factors of 16p, 28
16p = 4 . 4 . p
28 = 4 . 7
Use the distributive property to factor out 4
16p – 28 = 4(4p) – 4(7)
= 4(4p – 7)
Question 37.

Answer:
Correct.
Explanation:
Find the factors of 2/3y, 14/3
2/3y = 2 . 1/3 . y
14/3 = 2 . 7 . 1/3
Use the distributive property to factor out 2/3
2/3y – 14/3 = 2/3(y) – 2/3(7)
= 2/3(y – 7)
FACTORING OUT A NEGATIVE NUMBER
Factor out the indicated number.
Question 38.
Factor -4 out of -8d + 20.
Answer:
-4(2d – 5)
Explanation:
Given expression is -8d + 20
Find factors of 8d, 20
-8d = -4 . 2 . d
20 = -4. -5
Use the distributive property to factor out -4
-8d + 20 = -4(2d) – 4(-5)
= -4(2d – 5)
Question 39.
Factor -6 out of 18z – 15.
Answer:
18z – 15 = -6(-3z + 5/2)
Explanation:
Given expression is 18z – 15
Find factors of 18z, -15
18z = -6 . -3 . z
-15 = -3 . 5/2 . 2
Use the distributive property to factor out -6
18z – 15 = -6(-3z) – 6(5/2)
= -6(-3z + 5/2)
Question 40.
Factor -0.25 out of 7g+ 3.5.
Answer:
7g+ 3.5 = -0.25(-28g – 14)
Explanation:
Given expression is 7g+ 3.5
Find factors of 7g, 3.5
7g = -0.25 x -28 x g
3.5 = -0.25 x -14
Use the distributive property to factor out -0.25
7g+ 3.5 = -0.25(-28g) -0.25(-14)
= -0.25(-28g – 14)
Question 41.
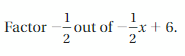
Answer:
-1/2 x + 6 = -1/2(x – 12)
Explanation:
Given expression is -1/2 x + 6
Find factors of -1/2 x, 6
-1/2x = -1/2 . x
6 = -1/2 . -4 . 3
Use the distributive property to factor out -1/2
-1/2 x + 6 = -1/2(x) – 1/2(-12)
= -1/2(x – 12)
Question 42.
Factor -1.75 out of -14m – 5.25n.
Answer:
-14m – 5.25n = -1.75(8m + 3n)
Explanation:
Given expression is -14m – 5.25n
Find factors of -14m, -5.25n
-14m = -1.75 . 8 . m
-5.25n = -1.75 . 3 . n
Use the distributive property to factor out -1.75
-14m – 5.25n = -1.75(8m) -1.75(3n)
= -1.75(8m + 3n)
Question 43.
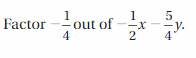
Answer:
-1/2 x – 5/4 y = -1/4(2x + 5y)
Explanation:
Given expression is -1/2 x – 5/4 y
Find factors of -1/2 x, – 5/4 y
-1/2x = -1/4 . 2. x
-5/4y = -1/4 . 5 . y
Use the distributive property to factor out -1/4
-1/2 x – 5/4 y = -1/4(2x) -1/4(5y)
= -1/4(2x + 5y)
Question 44.
STRUCTURE
A rectangle has an area of (4x + 12) square units. Write three multiplication expressions that can represent the product of the length and the width of the rectangle.
Answer:
Three multiplication expressions that can represent the product of the length and the width of the rectangle are1/2(4x + 24), 2(2x + 6), 4(x + 3).
Explanation:
Rectangle area is (4x + 12) square units
Find the factors of 4x, 12
4x = 2 . 2 . x
12 = 2 . 2 . 3
Use the distributive property to factor out 2
(4x + 12) = 2(2x) + 2(6)
= 2(2x + 6)
Area of rectangle = length . width
= 2(2x + 6)
Use the distributive property to factor out 4 of (4x + 12)
(4x + 12) = 4(x) + 4(3)
= 4(x + 3)
4x = 1/2 . 4x
12 = 1/2 . 6 . 4
Use the distributive property to factor out 1/2
(4x + 12) = 1/2(4x) + 1/2(24)
= 1/2(4x + 24)
So, three multiplication expressions that can represent the product of the length and the width of the rectangle are1/2(4x + 24), 2(2x + 6), 4(x + 3).
Question 45.
MODELING REAL LIFE
A square wrestling mat has a perimeter of (12x – 32) feet. Explain how to use the expression to find the length (in feet) of the mat. Justify your answer.

Answer:
The expression that represents the length of the side of the mat is 3x – 8 feet.
Explanation:
The wrestling mat is a sqauare
Let a is the length of the side of a square
The perimeter of mat = 4 x side = 4 . a
12x – 32 = 4a
In order to find the length of the side of te mat we have to solve the equation above for a
4a = 12x – 32
a = (12x – 32)/4
a = 3x – 8 feet
The expression that represents the length of the side of the mat is 3x – 8 feet.
Question 46.
MODELING REAL LIFE
A table is 6 feet long and 3 feet wide. You extend the length of the table by inserting two identical leaves table. The extended table is rectangular with an area of (18 + 6x) square feet. Write and interpret an expression that represents the length (in feet) of the extended table.
Answer:
The length of the extended table is 6 + 2x
Explanation:
A table is 6 feet long and 3 feet wide.
Table area = length. width
= 6 . 3 = 18 sq feet
The extended table is rectangular with an area of (18 + 6x) square feet.
Find factors of 18, 6x
18 = 3 . 6
6x = 3 . 2 . x
(18 + 6x) = 3(6) + 3(2x)
= 3(6 + 2x)
So, the length of the extended table is 6 + 2x
Question 47.
DIG DEEPER!
A three-dimensional printing pen uses heated plastic to create three-dimensional objects. A kit comes with one 3D-printing pen and packages of plastic. An art club purchases 6 identical kits for (180 + 58.5p) dollars. Write and interpret an expression that represents the cost of one kit.

Answer:
The cost of one kit is (30 + 9.75) dollars.
Explanation:
Art club purchases 6 identical kits for (180 + 58.5p) dollars
Divide (180 + 58.5p) by 6 to get the cost of one kit
= (180 + 58.5p) / 6
= 180/6 + 58.5p/6
= 30 + 9.75
Hence, the cost of one kit is (30 + 9.75) dollars.
Question 48.
STRUCTURE
The area of the trapezoid is ![]() square centimeters. Write two different pairs of expressions that represent the possible base lengths (in centimeters). Justify your answers.
square centimeters. Write two different pairs of expressions that represent the possible base lengths (in centimeters). Justify your answers.
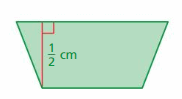
Answer:
(3x – 1)/2
Explanation:
Area of the trapezoid = height * (sum of parallel lengths)/2
= (3x/4 – 1/4)
= (3x – 1)/4
Here height is 1/2
So, base length is (3x – 1)/2
Expressions Connecting Concepts
3 Connecting Concepts
Using the Problem-Solving Plan
Question 1.
The runway shown has an area of (0.05x + 0.125) square miles. Write an expression that represents the perimeter (in feet) of the runway.

Understand the problem
You know the area of the rectangular runway in square miles and the width of the runway in miles. You want to know the perimeter of the runway in feet.
Make a plan.
Factor the width of 0.05 mile out of the expression that represents the area to find an expression that represents the length of the runway. Then write an expression that represents the perimeter (in miles) of the runway. Finally, use a measurement conversion to write the expression in terms of feet.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
The perimeter of the runway is 2(x + 2.55) miles.
Explanation:
The runway shown has an area of (0.05x + 0.125)
= 0.05(x) + 0.05(2.5)
= 0.05(x + 2.5)
The length of the run way is (x + 2.5) miles
Width = 0.05
Perimeter of the runway = 2(length + width)
= 2(x + 2.5 + 0.05)
= 2(x + 2.55)
Question 2.
The populations of two towns after t years can be modeled by -300t + 7000 and -200t + 5500. What is the combined population of the two towns after years? The combined population of the towns in Year 10 is what percent of the combined population in Year 0?

Answer:
The combined population of two towns after t years is -500t + 12500.
The combined population of the towns in 10 Years is 60% of the combined population in Year 0.
Explanation:
The populations of two towns after t years can be modeled by -300t + 7000 and -200t + 5500
The combined population of two towns after t years = -300t + 7000 + (-200t + 5500)
= -300t + 7000 – 200t + 5500
= -500t + 12500
The combined population of the towns in 10 Years = -500(10) + 12500
= -5000 + 12500 = 7500
The combined population in Year 0 = -500(0) + 12500
= 12500
The combined population of the towns in 10 Years is what percent of the combined population in Year 0 is 7500/12500 x 100
= 7500/125 = 60
So, The combined population of the towns in 10 Years is 60% of the combined population in Year 0.
Performance Task
Chlorophyll in Plants
At the beginning of this chapter, you watched a STEAM Video called “Tropic Status.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Expressions Chapter Review
3 Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.
Graphic Organizers
You can use an Example and Non-Example Chart to list examples and non-examples of a concept. Here is an Example and Non-Example Chart for like terms.
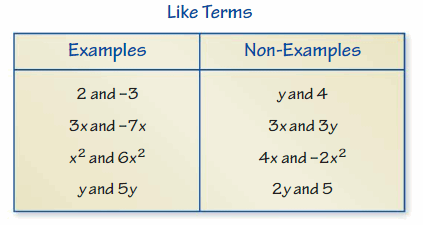
Choose and complete a graphic organizer to help you study the concept.
- simplest form
- equivalent expressions
- linear expression
- Distributive Property
- factoring an expression

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

3.1 Algebraic Expressions (pp. 91–96)
Identify the terms and like terms in the expression.
Question 1.
z + 8 – 4z
Answer:
Like terms are z, -4z
Terms are z, 8, -4z
Explanation:
Like terms are z, -4z
Terms are z, 8, -4z
Question 2.
3n + 7 – n – 3
Answer:
Like terms are 3n, -n
Terms are 3n, 7, -n, -3
Explanation:
Like terms are 3n, -n
Terms are 3n, 7, -n, -3
Question 3.
10x2 – y + 12 – 2x2
Answer:
Like terms are10x², -2x²
Terms are 10x², -y, 12, -2x²
Explanation:
Like terms are10x², -2x²
Terms are 10x², -y, 12, -2x²
Simplify the expression.
Question 4.
4h – 8h
Answer:
4h – 8h = -4h
Explanation:
The given expression is 4h – 8h
= -4h
Question 5.
6.4r – 7 – 2.9r
Answer:
6.4r – 7 – 2.9r = 3.5r – 7
Explanation:
The given expression is 6.4r – 7 – 2.9r
= 3.5r – 7
Question 6.
2m – m – 7m
Answer:
2m – m – 7m = -6m
Explanation:
The given expression is 2m – m – 7m
= 2m – 8m = -6m
Question 7.
6y + 9 + 3y – 7
Answer:
6y + 9 + 3y – 7 = 9y + 2
Explanation:
The given expression is 6y + 9 + 3y – 7
= 9y + 2
Question 8.
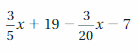
Answer:
3/5 x + 19 – 3/20 x – 7 = 9x/20 + 12
Explanation:
The given expression is 3/5 x + 19 – 3/20 x – 7
= 3x/5 + 19 – 3x/20 – 7
= (12x – 3x)/20 + 19 – 7
= 9x/20 + 12
Question 9.
![]()
Answer:
2/3 y + 14 – 1/6 y – 8 = y/2 + 6
Explanation:
The given expression is 2/3 y + 14 – 1/6 y – 8
= (4y – y)/6 + 14 – 8
= 3y/6 + 6
= y/2 + 6
Question 10.
Write an expression with 4 different terms that is equivalent to 5x2 – 8. Justify your answer.
Answer:
5x² – 8 = 3x² + 2x² – 6 – 2
Explanation:
Given expression is 5x² – 8
= 3x² + 2x² – 6 – 2
Question 11.
Find the earnings for selling the same number of each type of sandwich. Justify your answer.
Answer:
The earnings in turkey is 2.25x + 1.15y
The earnings in Ham is 1.55x + 1.30y
Explanation:
Let us take the earnings for selling pretzel roll sandwich is x, begel sandwich is y
So, The earnings in turkey is 2.25x + 1.15y
The earnings in Ham is 1.55x + 1.30y
Question 12.
You buy the same number of brushes, rollers, and paint cans.
a. Write and interpret an expression in simplest form that represents the total amount of money you spend on painting supplies.
b. How much do you spend when you buy one set of supplies for each of 3 painters?

Answer:
a. The total amount of money you spend on painting supplies is 32.67x
b. The cost of one set of supplies for each of 3 painters is $98.01.
Explanation:
a.
let us take you buy the x number of brushes, rollers, and paint cans.
So, the amount sped to buy those is 3.99x + 21.79x + 6.89x
= x(3.99 + 21.79 + 6.89)
= x(32.67)
b. The cost for 1 set of painting supplies = (3.99 + 21.79 + 6.89)
= 32.67
The cost for 3 sets of painting supplies = 3(32.67)
= 98.01
3.2 Adding and Subtracting Linear Expressions (pp. 97–102)
Find the sum.
Question 13.
(c – 4) + (3c + 9)
Answer:
(c – 4) + (3c + 9) = 4c + 5
Explanation:
The given expression is (c – 4) + (3c + 9)
= c – 4 + 3c + 9
= 4c + 5
Question 14.
(5z + 4) + (3z – 6)
Answer:
(5z + 4) + (3z – 6) = 8z- 2
Explanation:
The given expression is (5z + 4) + (3z – 6)
= 5z + 4 + 3z – 6
= 8z- 2
Question 15.
(-2.1m – 5) + (3m – 7)
Answer:
(-2.1m – 5) + (3m – 7) = 0.9m – 12
Explanation:
The given expression is (-2.1m – 5) + (3m – 7)
= -2.1m – 5 + 3m – 7
= 0.9m – 12
Question 16.
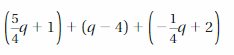
Answer:
(5/4 q + 1) + (q – 4) + (-1/4 q + 2) = 2q – 1
Explanation:
The given expression is (5/4 q + 1) + (q – 4) + (-1/4 q + 2)
= 5/4 q + 1 + q – 4 -1/4 q + 2
= (5q – q)/4 + q + 3 – 4
= 4q/4 + q – 1
= q + q – 1
= 2q – 1
Find the difference.
Question 17.
(x – 1) – (3x + 2)
Answer:
(x – 1) – (3x + 2) = -2x – 3
Explanation:
The given expression is (x – 1) – (3x + 2)
= x – 1 – 3x – 2
= -2x – 3
Question 18.
(4y + 3) – (2y – 9)
Answer:
(4y + 3) – (2y – 9) = 2y + 12
Explanation:
The given expression is (4y + 3) – (2y – 9)
= 4y + 3 – 2y + 9
= 2y + 12
Question 19.
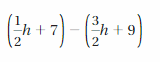
Answer:
(1/2 h + 7) – (3/2 h + 9) = -h – 2
Explanation:
The given expression is (1/2 h + 7) – (3/2 h + 9)
= 1/2 h + 7 – 3/2 h – 9
= (1 – 3)/2 h – 2
= -2h/2 – 2
= -h – 2
Question 20.
(4 – 3.7b) – (-5.4b – 4) – (1.2b + 1)
Answer:
(4 – 3.7b) – (-5.4b – 4) – (1.2b + 1) = 7 – 0.5b
Explanation:
The given expression is (4 – 3.7b) – (-5.4b – 4) – (1.2b + 1)
= 4 – 3.7b + 5.4b + 4 – 1.2b – 1
= 7 – 4.9b + 5.4b
= 7 – 0.5b
Question 21.
A basket holds apples. You pick (2n – 3) apples, and your friend picks (n + 4) apples. How many apples do you and your friend pick together? How many baskets do you need to carry all the apples? Justify your answer.
Answer:
The number of apples you and your friend picked is 3n + 1.
Explanation:
The number of apples you picked = 2n – 3
The number of apples your friend picked = n + 4
The number of apples you and your friend picked = (2n – 3) + (n + 4)
= 3n + 1
The number of apples you and your friend picked is 3n + 1
Question 22.
Greenland has a population of x people. Barbados has a population of about 4500 more than 5 times the population of Greenland. Find and interpret the difference in the populations of these two countries.
Answer:
The difference in the populations of these two countries is 4500 + 4x.
Explanation:
Greenland population = x
Barbados population = 4500 + 5x
The difference in the populations of these two countries = 4500 + 5x – x
= 4500 + 4x
3.3 The Distributive Property (pp. 103–108)
Simplify the expression.
Question 23.
2(a – 3)
Answer:
2(a – 3) = 2a – 6
Explanation:
The given expression is 2(a – 3)
= 2(a) – 2(3)
= 2a – 6
Question 24.
-3(4x – 10)
Answer:
-3(4x – 10) = -12x + 30
Explanation:
The given expression is -3(4x – 10)
= -3(4x) + 3(10)
= -12x + 30
Question 25.
-2.5(8 – b)
Answer:
-2.5(8 – b) = -20 + 2.5b
Explanation:
The given expression is -2.5(8 – b)
= -2.5(8) + 2.5(b)
= -20 + 2.5b
Question 26.
-7(1 – 3d – 5)
Answer:
-7(1 – 3d – 5) = 21d + 28
Explanation:
The given expression is -7(1 – 3d – 5)
= -7(-3d – 4)
= -7(-3d) – 7(-4)
= 21d + 28
Question 27.
9(-3w – 6.2 + 2w)
Answer:
9(-3w – 6.2 + 2w) = -9w – 55.8
Explanation:
The given expression is 9(-3w – 6.2 + 2w)
= 9(-w – 6.2)
= 9(-w) – 9(6.2)
= -9w – 55.8
Question 28.
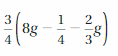
Answer:
3/4 (8g – 1/4 – 2/3 g) = 11g/2 – 3/8
Explanation:
The given expression is 3/4 (8g – 1/4 – 2/3 g)
= 3/4((24g – 2g)/3 – 1/4)
= 3/4(22g/3 – 1/4)
= 3/4(22g/3) – 3/4(1/4)
= 11g/2 – 3/8
Question 29.
Mars has m moons. The number of moons of Pluto is one more than twice the number of moons of Mars. The number of moons of Neptune is one less than 3 times the number of moons of Pluto. Write and interpret a simplified expression that represents the number of moons of Neptune.

Answer:
The number of moons of Neptune is 6m + 2.
Explanation:
Number of moons of marks = m
The number of moons of pluto = 1 + 2m
The number of moons of Neptune = 3(1 + 2m) – 1
= 3 + 6m – 1 = 6m + 2
Simplify the expression.
Question 30.
3( 2 + q) + 15
Answer:
3( 2 + q) + 15 = 21 + 3q
Explanation:
The given expression is 3( 2 + q) + 15
= 3(2) + 3(q) + 15
= 6 + 3q + 15
= 21 + 3q
Question 31.
![]()
Answer:
1/8 (16m – 8) – 17 = 2m – 18
Explanation:
The given expression is 1/8 (16m – 8) – 17
= 1/8(16m) + 1/8(-8) – 17
= 2m – 1 – 17
= 2m – 18
Question 32.
-1.5(4 – n) + 2.8
Answer:
-1.5(4 – n) + 2.8 = -3.2 + 1.5n
Explanation:
The given expression is -1.5(4 – n) + 2.8
= -1.5(4)- 1.5(-n) + 2.8
= -6 + 1.5n + 2.8
= -3.2 + 1.5n
Question 33.
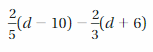
Answer:
2/5 (d – 10) – 2/3 (d + 6) = -4d/15 – 8
Explanation:
The given expression is 2/5 (d – 10) – 2/3 (d + 6)
= 2/5(d) + 2/5(-10) – 2/3(d) – 2/3(6)
= 2d/5 – 4 – 2d/3 – 4
= (6d – 10d)/15 – 8
= -4d/15 – 8
Question 34.
The expression for degrees Fahrenheit is ![]() where C represents degrees Celsius. The temperature today is 5 degrees Celsius more than yesterday. Write and simplify an expression for the difference in degrees Fahrenheit for these two days.
where C represents degrees Celsius. The temperature today is 5 degrees Celsius more than yesterday. Write and simplify an expression for the difference in degrees Fahrenheit for these two days.
Answer:
The difference in degrees Fahrenheit for these two days 9 degrees celsius.
Explanation:
The expression for degrees Fahrenheit is 9/5 C + 32
The temperature today is 5 degrees Celsius more than yesterday.
Today temperature = 9/5 (x + 5) + 32
Yesterday Temperature = 9/5 x + 32
The difference in degrees Fahrenheit for these two days = 9/5 (x + 5) + 32 – ( 9/5 x + 32)
= 9/5(x) + 9/5(5) + 32 – 9/5 x – 32
= 9x/5 + 9 + 32 – 9x/5 – 32
= 9
3.4 Factoring Expressions (pp. 109–114)
Factor the expression using GCF.
Question 35.
18a – 12
Answer:
18a – 12 = 6(3a – 2)
Explanation:
The G.C.F of 18a, 12 is
18a = 2 . 3 . 3 . a
12 = 3 . 2 . 2
The common prime factors are 2 . 3 = 6
The G.C.F of 18a, 12 is 6
Use the GCF to factor the expression
18a – 12 = 6(3a) – 6(2)
= 6(3a – 2)
Question 36.
2b + 8
Answer:
2b + 8 = 2(b + 3)
Explanation:
The G.C.F of 2b, 8 is
2b = 2 . b
8 = 2 . 2 . 2
The common prime factors are 2
The G.C.F of 2b, 8 is 2
Use the GCF to factor the expression
2b + 8 = 2(b) + 2(3)
= 2(b + 3)
Question 37.
9 – 15x
Answer:
9 – 15x = 3(3 – 5x)
Explanation:
The G.C.F of 9, 15x is
9 = 3 . 3
15x = 3 . 5 . x
The common prime factor is 3
The G.C.F of 9, 15x is 3
Use the GCF to factor the expression
9 – 15x = 3(3) – 3(5x)
= 3(3 – 5x)
Factor out the coefficient of the variable term.
Question 38.
![]()
Answer:
1/4 y + 3/8 = 1/4(y + 3/2)
Explanation:
Find the factors of 1/4 y, 3/8
1/4y = 1/4 . y
3/8 = 1/4 . 1/2 . 3
Use the distributive property to factor out 1/4
1/4 y + 3/8 = 1/4(y) + 1/4(3/2)
= 1/4(y + 3/2)
Question 39.
1.7j – 3.4
Answer:
1.7j – 3.4 = 1.7(j – 2)
Explanation:
Find the factors of 1.7j, 3.4
1.7j = 1.7 . j
3.4 = 1.7 . 2
Use the distributive property to factor out 1.7
1.7j – 3.4 = 1.7(j) – 1.7(2)
= 1.7(j – 2)
Question 40.
-5p + 20
Answer:
-5p + 20 = 5(-p + 4)
Explanation:
Find the factors of 5p, 20
5p = 5 . p
20 = 5 . 4
Use the distributive property to factor out 5
-5p + 20 = 5(-p) + 5(4)
= 5(-p + 4)
Question 41.
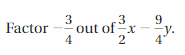
Answer:
3/2 x – 9/4y = -3/4(-2 + 3y)
Explanation:
Find the factors of 3/2 x , -9/4 y
3/2x = -3/4 . -2
-9/4 y = -3/4 . 3 . y
Use the distributive property to factor out -3/4
3/2 x – 9/4y = -3/4(-2) – 3/4(3y)
= -3/4(-2 + 3y)
Question 42.
You and 4 friends are buying tickets for a concert. The cost to buy one ticket is c dollars. If you buy all the tickets together, there is a discount and the cost is (5c – 12.5) dollars. How much do you save per ticket when you buy the tickets together?
Answer:
The amount saved by buying all tickets is 12.5 dollars.
Explanation:
The cost per 1 ticket is c
The cost to buy 5 tickets = 5c dollars
If you buy all the tickets together, there is a discount and the cost is (5c – 12.5) dollars
The amount saved by buying all tickets = 5c – (5c – 12.5) dollars
= 5c – 5c + 12.5
= 12.5 dollars
Question 43.
The rectangular pupil of an octopus is estimated to be 20 millimeters long with an area of (20x – 200) square millimeters. Write an expression that represents the perimeter (in millimeters) of the octopus pupil.

Answer:
Perimeter the octopus pupil is 2x milli meters.
Explanation:
The length of an octopus pupil = 20 millimeters
Area of an octopus = (20x – 200) sq milli meters
Factor 20 out of (20x – 200)
= 20(x) – 20(10)
= 20(x – 20)
So, the width of the octopus pupil = x – 20 milli meters
The perimeter of octopus pupil = 2(length + width)
= 2(20 + (x – 20))
= 2(20 + x – 20)
= 2x milli meters
Perimeter the octopus pupil is 2x milli meters.
Question 44.
A building block has a square base that has a perimeter of (12x – 9) inches. Explain how to use the expression to find the length (in inches) of the wall shown.
Answer:
The length of the wall is 7(3x – 9/4) inches
Explanation:
The perimeter of the square base = (12x – 9) inches
4 x length of the base = (12x – 9)
length of the base = (12x/4 – 9/4)
= (3x – 9/4) inches
The length of wall = 7(3x – 9/4)
Expressions Practice Test
3 Practice Test
Question 1.
Identify the terms and like terms in 4x + 9x2 – 2x + 2.
Answer:
The terms are 4x, 9x², -2x, 2
The like terms are 4x -2x
Explanation:
The given expression is 4x + 9x² – 2x + 2
The terms are 4x, 9x², -2x, 2
The like terms are 4x -2x
Simplify the expression.
Question 2.
8x – 5 + 2x
Answer:
8x – 5 + 2x = 10x – 5
Explanation:
The given expression is 8x – 5 + 2x
= 10x – 5
Question 3.
2.5w – 3y + 4w
Answer:
2.5w – 3y + 4w = 6.5w – 3y
Explanation:
The given expression is 2.5w – 3y + 4w
= 6.5w – 3y
Question 4.
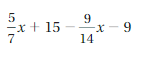
Answer:
5/7 x + 15 – 9/14 x – 9 = x/14 + 6
Explanation:
The given expression is 5/7 x + 15 – 9/14 x – 9
= (10x – 9x)/14 + 15 – 9
= x/14 + 6
Question 5.
(3j + 11) + (8j – 7)
Answer:
(3j + 11) + (8j – 7) = 11j + 4
Explanation:
The given expression is (3j + 11) + (8j – 7)
= 3j + 11 + 8j – 7
= 11j + 4
Question 6.
(2r – 13) – (-6r + 4)
Answer:
(2r – 13) – (-6r + 4) = 8r – 17
Explanation:
The given expression is (2r – 13) – (-6r + 4)
= 2r – 13 + 6r – 4
= 8r – 17
Question 7.
-2(4 – 3n)
Answer:
-2(4 – 3n) = -8 + 6n
Explanation:
The given expression is -2(4 – 3n)
= -2(4) – 2(-3n)
= -8 + 6n
Question 8.
3(5 – 2n) + 9n
Answer:
3(5 – 2n) + 9n = 15 + 3n
Explanation:
The given expression is 3(5 – 2n) + 9n
= 3(5) – 3(2n) + 9n
= 15 – 6n + 9n
= 15 + 3n
Question 9.
![]()
Answer:
1/3 (6x + 9) – 2 = 2x + 1
Explanation:
The given expression is 1/3 (6x + 9) – 2
= 1/3 (6x) + 1/3(9) – 2
= 2x + 3 – 2
= 2x + 1
Question 10.
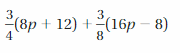
Answer:
3/4 (8p + 12) + 3/8 (16p – 8) = 12p + 6
Explanation:
The given expression is 3/4 (8p + 12) + 3/8 (16p – 8)
= 3/4(8p) + 3/4(12) + 3/8(16p) + 3/8(-8)
= 3(2p) + 3(3) + 3(2p) + 3(-1)
= 6p + 9 + 6p – 3
= 12p + 6
Question 11.
-2.5(2s – 5) – 3(4.5s – 5.2)
Answer:
-2.5(2s – 5) – 3(4.5s – 5.2) = -18.5s + 28.1
Explanation:
The given expression is -2.5(2s – 5) – 3(4.5s – 5.2)
= -2.5(2s) – 2.5(-5) – 3(4.5s) – 3(-5.2)
= -5s + 12.5 – 13.5s + 15.6
= -18.5s + 28.1
Factor out the coefficient of the variable term.
Question 12.
6n – 24
Answer:
6n – 24 = 6(n – 4)
Explanation:
Find the factors of 6n, 24
6n = 6 . n
24 = 6 . 4
Use the distributive property to factor out 6
6n – 24 = 6(n) – 6(4)
= 6(n – 4)
Question 13.
![]()
Answer:
1/2 q + 5/2 = 1/2(q + 5)
Explanation:
Find the factors of 1/2 q, 5/2
1/2q = 1/2 . q
5/2 = 5 . 1/2
Use the distributive property to factor out 1/2
1/2 q + 5/2 = 1/2(q) + 1/2(5)
= 1/2(q + 5)
Question 14.
-4x + 36
Answer:
-4x + 36 = 4(-x + 9)
Explanation:
Find the factors of 4x, 36
4x = 4 . x
36 = 4 . 9
Use the distributive property to factor out 4
-4x + 36 = 4(-x) + 4(9)
= 4(-x + 9)
Question 15.
Find the earnings for giving a haircut and a shampoo to m men and w women. Justify your answer.
Answer:
The earnings for giving a haircut and a shampoo to women is 45w + 12w
The earnings for giving a haircut and a shampoo to men is 15m + 7m
Explanation:
The earning for giving haircut to women is 45w
The earning for giving shampoo to women is 12w
The earning for giving haircut to men is 15m
The earning for giving shampoo to men is 7m
The earnings for giving a haircut and a shampoo to women is 45w + 12w
The earnings for giving a haircut and a shampoo to men is 15m + 7m
Question 16.
The expression 15x + 11 represents the perimeter of the trapezoid. What is the length of the fourth side? Explain your reasoning.
Answer:
The length of the fourth side of trapezoid is 6x + 5.
Explanation:
Perimeter of the trapezoid = 15x + 11
2x + 3 + 3x + 4 + 4x – 1 + fourth side length = 15x + 11
9x + 7 – 1 + fourth side length = 15x + 11
9x + 6 + fourth side length = 15x + 11
fourth side length = (15x + 11) – (9x + 6)
= 15x + 11 – 9x – 6
= 6x + 5
Question 17.
The maximum number of charms that will fit on a bracelet is 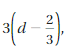 , where d is the diameter(in centimeters) of the bracelet.
, where d is the diameter(in centimeters) of the bracelet.
a. Write and interpret a simplified expression that represents the maximum number of charms on a bracelet.
b. What is the maximum number of charms that fit on a bracelet that has a diameter of 6 centimeters?
Answer:
a. The maximum number of charms that will fit on a bracelet = 3d – 2
b. The maximum number of charms that fit on a bracelet that has a diameter of 6 centimeters is 16.
Explanation:
a. The maximum number of charms that will fit on a bracelet = 3(d – 2/3)
= 3(d) – 3(2/3)
= 3d – 2
b. The maximum number of charms that fit on a bracelet that has a diameter of 6 centimeters is 3(6) – 2
= 18 – 2 = 16
Question 18.
You expand a rectangular garden so the perimeter is now twice the perimeter of the old garden. The expression 12w + 16 represents the perimeter of the new garden, where w represents the width of the old garden.
a. Write an expression that represents the perimeter of the old garden. Justify your answer.
b. Write an expression that represents the area of the old garden.
Answer:
a. Perimeter of old rectangular garden is 6w + 8
b. The area of the old garden is 12w.
Explanation:
a. New garden perimeter = 2 * perimeter of old garden
(12w + 16) = 2 * perimeter of old garden
(12w/2 + 16/2) = Perimeter of old garden
6w + 8 = Perimeter of old garden
b. Perimeter of old rectangular garden is 6w + 8
Find the factors of 6w, 8
6w = 2 . 3 . w
8 = 2 . 2 . 2
Use the distributive property to factor out 2
6w + 8 = 2(3w) + 2(4)
= 2(3w + 4)
Perimeter of old garden = 2(length + width) = 2(3w + 4)
So, length of the garden is 3w, width of the garden is 4
The area of old garden = length . width
= 3w . 4 = 12w
Expressions Cumulative Practice
Question 1.
What is the simplified form of the expression?
![]()
A. -3.6x
B. 6x – 5
C. 1.4x – 5
D. 3.7x – 7.3

Answer:
C. 1.4x – 5
Explanation:
The given expression is 3.7x – 5 – 2.3x
= 1.4x – 5
Question 2.
What is the value of the expression when c = 0 and d = -6?

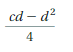
Answer:
-9.
Explanation:
The give expression is (cd – d²)/4
Put c = 0, d= -6 in above expression
= (0 . -6 – (-6)²)/4
= -(36)/4
= -9
Question 3.
What is the value of the expression?
![]()
F. -52
G. -24
H. 24
I. 52
Answer:
G. -24
Explanation:
The given expression is -38 – (-14)
= -38 + 14 = -24
Question 4.
The daily low temperatures for a week are shown.
What is the mean low temperature of the week?
A. −2°F
B. 6°F
C. 8°F
D. 10°F
Answer:
The mean low temperature of the week is 6°F.
Explanation:
The list of low temperatures are -2°F, -3°F, -1°F, 8°F, 10°F, 12°F, 18°F
The mean temperature of the week = sum of the observations/ number of observations
= (-2 – 3 – 1 + 8 + 10 + 12 + 18)/7
= (-6 + 48)/7
= 42/7
= 6°F
The mean low temperature of the week is 6°F.
Question 5.
You and a friend collect seashells on a beach. After h minutes, you have collected (11 + 2h) seashells and your friend has collected (5h – 2) seashells. How many total seashells have you and your friend collected?
F. 7h + 9
G. 3h – 13
H. 16h
I. 7h + 13
Answer:
F. 7h + 9
Explanation:
The number of seashells collected by you = (11 + 2h)
The number of seashells collected by your friend = (5h – 2)
The total seashells have you and your friend collected = The number of seashells collected by you + The number of seashells collected by your friend
= 11 + 2h + 5h – 2
= 9 + 7h
Question 6.
What is the value of the expression?
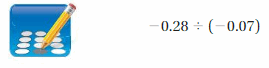
Answer:
-0.28 ÷ (-0.07) = 4
Explanation:
The value of the expression is -0.28 ÷ (-0.07)
= 0.28 ÷ 0.07 = 4
Question 7.
Which list is ordered from least to greatest?

Answer:
D.
Explanation:
A. -3/4, -1/2, 3/8, -1/4, 7/8 is not in the order
B. -1/2, -1/4, 3/8, -3/4, 7/8 is not in the order
C. 7/8, 3/8, -1/4, -1/2, -3/4 is not in the order
D. -3/4, -1/2, -1/4, 3/8, 7/8 is in the order from least to greatest.
Question 8.
Which number is equivalent to the expression shown?
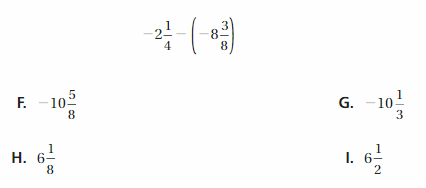
Answer:
H. 6(1/8)
Explanation:
-2(1/4) – (-8(3/8)) = -9/4 + 67/8
= (-18 + 67)/8 = 49/8
= 6(1/8)
Question 9.
What is the simplified form of the expression?
![]()
A. 15x + 30
B. x – 12
C. 13x + 12
D. -11x
Answer:
B. x – 12
Explanation:
The given expression is 7x – 2(3x + 6)
= 7x – 2(3x) – 2(6)
= 7x – 6x – 12
= x – 12
Question 10.
Which expression is not equivalent to the expression?
![]()
F. 6(12m – 10)
G. 4(18m – 15)
H. 12m
I. 12(6m – 5)
Answer:
I. 12(6m – 5)
Explanation:
The given expression is 72m – 60
Find the factors of 72m, 60
72m = 2 . 2 . 3 . 3 . 2 . m
60 = 2 . 2 . 3 . 5
The G.C.F of 72m, 60 is 2 . 2 . 3 = 12
72m – 60 = 12(6m) – 12(5)
= 12(6m – 5)
Question 11.
You want to buy a bicycle with your friend. You have $43.50 saved and plan to save an additional $7.25 every week. Your friend has $24.50 saved and plans to save an additional $8.75 every week.

Part A
Simplify and interpret an expression that represents the amount of money you and your friend save after weeks.
Part B
After 10 weeks, you and your friend use all of the money and buy the bike. How much does the bike cost? Who pays more towards the cost of the bike? Explain your reasoning.
Answer:
A. The total amount of money you and your friend saved after x weeks is 68 + 16x
B. The cost of the bike is 228 dollars
You will pay more money towards the bike.
Explanation:
A. Let the number of weeks we need to save be x
The amount you saved 43.50 + 7.25x
The amount your friend saved = 24.50 + 8.75x
The total amount of money you and your friend saved after x weeks is 43.50 + 7.25x + 24.50 + 8.75x
= 68 + 16x
B. The amount saved after 10 weeks is
The amount you saved = 43.50 + 7.25(10) = 43.50 + 72.5 = 116
The amount your friend saved = 24.50 + 8.75(10) = 24.50 + 87.5 = 112
The cost of bike = The amount you saved + The amount your friend saved
= 116 + 112 = 228 dollars
You will pay more money towards the bike.
Question 12.
Your friend evaluated 3 + x2 ÷ y when x = 2 and y = 4.
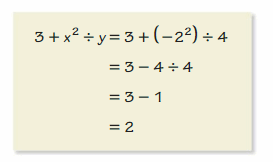
What should your friend do to correct his error?
A. Divide 3 by 4 before subtracting.
B. Square -2, then divide.
C. Divide -2 by 4, then square.
D. Subtract 4 from 3 before dividing.
Answer:
B. Square -2, then divide.
Explanation:
The given expression is 3 + x2 ÷ y
Put x = 2 and y = 4
= 3 + 2² ÷ 4
= 3 + 4 ÷ 4
= 3 + 1
= 4
Conclusion:
To help you out with Chapter 3 Expressions we have jotted down all the exercise problems in your Big Ideas Math Text Book 7th Grade Solution Key. Just tap on the respective link you wish to prepare and learn the fundamentals included within it easily. Bookmark our ccssmathanswers.com website to get the solutions of all Grade 7 chapters.