Are you searching for the Solution Key of Big Ideas Math 6th Grade Chapters? If your answer is yes, then you are on the right page. You can understand the concepts in-depth with the help of Big Ideas Math Book Solutions. We can provide the step by step explanations for all the questions using the Figures. Refer to our Big Ideas Math Book 6th Grade Answer Key Chapter 7 and solve the problems. You can easily understand the concepts with the help of the Big Ideas Math Book Solution Key. Get the pdf link of Big Ideas Math Answers Grade 6 Chapter 7 Area, Surface Area, and Volume from here.
Big Ideas Math Book 6th Grade Answer Key Chapter 7 Area, Surface Area, and Volume
In order to excel in the exam, we suggest the students of 6th standard to refer to the Big Ideas Math Book Answer Key Grade 6 Chapter 7 Area, Surface Area and Volume. Students who feel difficulty in solving the problems can easily and quickly understand the concepts with the help of Big Ideas Math Book Answer Key Chapter 7.
Performance
- Area, Surface Area, and Volume STEAM Video/Performance
- Area, Surface Area, and Volume Gettig Ready for chapter 7
Lesson: 1 Areas of Parallelograms
Lesson: 2 Areas of Triangles
Lesson: 3 Areas of Trapezoids and Kites
Lesson: 4 Three-Dimensional Figures
Lesson: 5 Surface Areas of Prisms
Lesson: 6 Surface Areas of Pyramids
Lesson: 7 Volumes of Rectangular Prisms
Chapter 7 – Area, Surface Area, and Volume
- Area, Surface Area, and Volume Connecting Concepts
- Area, Surface Area, and Volume Practice Test
- Area, Surface Area, and Volume Cumulative Practice
Area, Surface Area, and Volume STEAM Video/Performance
Packaging Design
Surface area can be used to determine amounts of materials needed to create objects. Describe another situation in which you need to find the surface area of an object.
Watch the STEAM Video “Packaging Design.” Then answer the following questions. Alex is cutting a design out of paper and folding it to form a box.

Question 1.
Tory says that the length of the design is 47 inches and the width is 16 inches. Show several ways that you can arrange three of the designs on a roll of paper that is 48 inches wide. You can make the length of the paper as long as is needed.
Answer:
We can make the length of the paper = 15.6666 inches
Explanation:
Given that the length of the design = 47 inches
that the width of the design = 16 inches
area of the design = 752 inches
They can arrange the three of the design on a roll of paper that = 48 inches
(752/48)
15.6666 inches
Question 2.
Tory says that the cut-out design has an area of 619 square inches. What is the least possible amount of paper that is wasted when you cut out three of the designs?

Answer:
The least amount of paper that is wasted when you cut out three of the designs = 12.89
Explanation:
The area of the rectangle = breadth x height
619 square inches = 48 in x length
619 = 48l
l = 619/48
l = 12.89
Performance Task
Maximizing the Volumes of Boxes
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given the dimensions of a small box and two larger boxes.
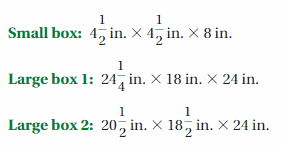
You will be asked to determine how many small boxes can be placed in each larger box. When a company is deciding on packaging for a product, why should the surface area of the packaging also be considered?

Area, Surface Area, and Volume Gettig Ready for chapter 7
Chapter Exploration
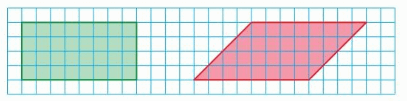
The formulas for the areas of polygons can be derived from one area formula, the area of a rectangle.
Work with a partner. Find (a) the dimensions of the figures and (b) the areas of the figures. What do you notice?
Question 1.
Answer:
The area of the rectangle = The product of the length and the product of the width
The area of the parallelogram = the product of the width and the product of the height
Explanation:
The area of the rectangle is equal to the area of the parallelogram
The area of the rectangle = the product of the length and the product of the width
The area of the rectangle = length x width
area = l x w
The area of the parallelogram = the product of the base and the product of the width
area = base x height
area = b x h
Question 2.
Answer:
The area of the rectangle = the product of the length and the product of the width
The area of the parallelogram = (1/2) x the product of the base and the product of the height
Explanation:
The area of the rectangle is equal to the area of the parallelogram
The area of the rectangle = the product of the length and the product of the width
The area of the rectangle = length x width
area = l x w
The area of the triangle =(1/2) x the product of the base and the product of the width
area =(1/2) base x height
area =(1/2) b x h
Question 3.
Answer:
The area of the rectangle = the product of the length and the product of the width
The area of the trapezoid = (1/2) x height x (base 1 + base 2)
Explanation:
The area of the rectangle is equal to the area of the parallelogram
The area of the rectangle = the product of the length and the product of the width
The area of the rectangle = length x width
area = l x w
The area of the trapezoid =(1/2) x product of the height and the product of the bases
area =(1/2) x height x bases
area =(1/2) x height (b1 + b2)
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.

Lesson 7.1 Areas of Parallelograms
A polygon is a closed figure in a plane that is made up of three or more line segments that intersect only at their endpoints. Several examples of polygons are parallelograms, rhombuses, triangles, trapezoids, and kites.
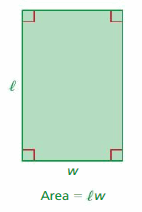
The formula for the area of a parallelogram can be derived from the definition of the area of a rectangle. Recall that the area of a rectangle is the product of its length ℓ and its width w. The process you use to derive this and other area formulas in this chapter is called deductive reasoning.
EXPLORATION 1
Deriving the Area Formula of a Parallelogram
Work with a partner.
a. Draw any rectangle on a piece of centimeter grid paper. Cut the rectangle into two pieces that can be arranged to form a parallelogram. What do you notice about the areas of the rectangle and the parallelogram?
b. Copy the parallelogram below on a piece of centimeter grid paper. Cut the parallelogram and rearrange the pieces to find its area.

c. Draw any parallelogram on a piece of centimeter grid paper and find its area. Does the area change when you use a different side as the base? Explain your reasoning.
d. Use your results to write a formula for the area A of a parallelogram.
Answer:
c : The area of the parallelogram = the product of the width and the product of the height
area = width x height
area = w x h
Yes the area changes.
We use the bases as equal length and width as equal length
d : the area of the parallelogram = the product of the width and the product of the height
c : The area of the parallelogram = the product of the width and the product of the height
area = width x height
area = w x h
Yes the area changes.
We use the bases as equal length and width as equal length
d : the area of the parallelogram = the product of the width and the product of the height
7.1 Lesson
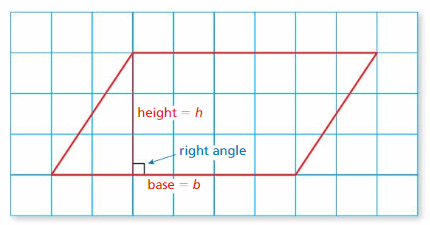
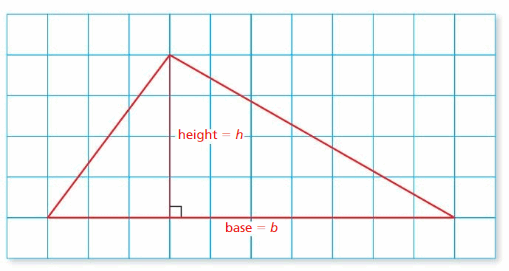
The area of a polygon is the amount of surface it covers. You can find the area of a parallelogram in much the same way as you can find the area of a rectangle.


Try It
Find the area of the parallelogram.
Question 1.
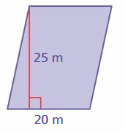
Answer:
Area = 500 m
Explanation:
The area of the parallelogram = the product of the base b and its height h.
area = b x h
b = 20 m, h = 25 m
So the Area of the parallelogram = 500 m
Question 2.
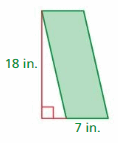
Answer;
Area = 126 in
Explanation:
The area of the parallelogram = the product of base b and its height h
area = b x h
b = 7 in , h = 18 in
So area = 126 in
Question 3.
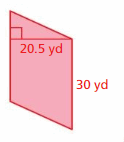
Answer:
615 yd
Explanation:
The area of the parallelogram = the product of base b and its height h
area = b x h
b = 30 yd, h = 20.5 yd
So area = 615 yd
When finding areas, you may need to convert square units. The diagrams at the left show that there are 9 square feet per square yard.
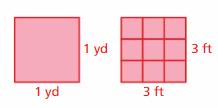
1 yd2 = (1 yd)(1 yd) = (3 ft)(3 ft) = 9 ft2
You can use a similar procedure to convert other square units.
Try It
Question 4.
Find the area of the parallelogram in square centimeters.
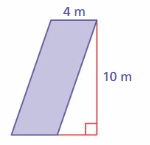
Answer:
The area of the parallelogram = the product of the base and the product of the height
Area = 400 cms
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = base x height
area = 4 m x 10 m
area = 40 m
1 meter = 100 centimeters
40 meter = 400 centimeters
area = 400 cm
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
WRITING
Explain how to use the area of a rectangle to find the area of a parallelogram
Answer:
Area of the rectangle = length x breadth
Area of the parallelogram = base x height
Explanation:
Area of the rectangle = length x breadth
area = l x b
Area of the parallelogram = base x height
area = b x h
area = bh
FINDING AREA
Find the area of the parallelogram.
Question 6.

Answer:
area = 80 ft
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = base x height
area = b x h
b = 16 ft and h = 5 ft given
area = 16 x 5
area = 80 ft
Question 7.
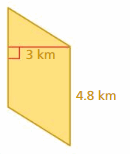
Answer:
The area of the parallelogram = 14 . 4 km
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = base x height
area = b x h
b = 3 km and h = 4.8 km given
area = 3 x 4.8
area = 14.4 km
Question 8.
REASONING
Draw a parallelogram that has an area of 24 square inches.
Answer:
We have to assume that the base = 4 square inches and the height = 6 square inches
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
The side of an office building in Hamburg, Germany, is in the shape of a parallelogram. The area of the side of the building is about 2150 square meters. What is the length x of the portion of the building that extends over the river?

Answer:
The length of the portion of the building that extends over the river = 45 m
Explanation:
The area of the parallelogram = the product of the bases and the product of the bases
area = 2150 square meters given
area = 25 m x (39 +47) given that height = 25 and base = 39
area = 25 x (86)
area = 2150
Thus the length of the portion of the building that extends over the river = 45 m
Question 10.
You make a photo prop for a school fair. You cut a 10-inch square out of a parallelogram-shaped piece of wood. What is the area of the photo prop?
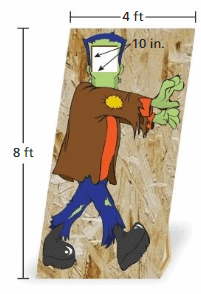
Answer:
The area of the photo prop = 32
Explanation:
the area of the photo prop = the product of the base and the product of the height
area = h x b
area = 8 x 4
area = 32 ft
Question 11.
DIG DEEPER!
A galaxy contains a parallelogram-shaped dust field. The dust field has a base of 150 miles. The height is 14% of the base. What is the area of the dust field?
Answer:
The area of the dust field =3,150
Explanation:
The area of the parallelogram = the product of the height and the product of the base
area = h x b given that height = 14% = (14/100) x 150 = 21, base = 150 miles
area = 3150
Areas of Parallelograms Homework & Practice 7.1
Review & Refresh
Graph the equation.
Question 1.
y = 4x
Answer:
: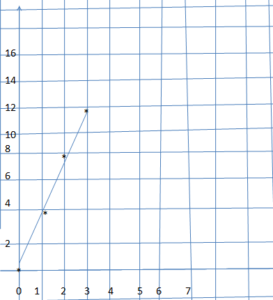
Explanation:
The given equation = y = 4x
for suppose x = 0, then y = 0
x = 1 , then y = 4 that means (1,4) y = 4 x 1 = 4
x = 2 , then y = 8 that means (2,8) y = 4 x 2 = 8
x = 3 , then y = 12 that means (3,12) y = 4 x 3 = 12
Question 2.
y = x + 3
Answer:
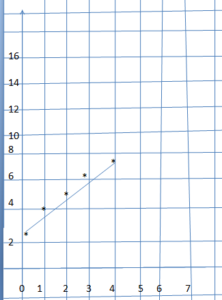
Explanation:
The given equation = y = x + 3
for suppose x = 0, then y = 3
x = 1 , then y = 4 that means (1,4) y = 1 + 3 = 4
x = 2 , then y = 5 that means (2, 5) y = 2 + 3 = 5
x = 3 , then y = 6 that means (3,16) y = 3 + 3 = 6
x = 4 , then y = 7 that means (4, 7) y = 4 + 3 = 7
Question 3.
y = 2x + 5
Answer:
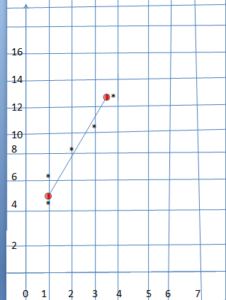
Explanation:
The given equation = y = 2x + 5
for suppose x = 0, then y = 5
x = 1 , then y = 7 that means (1,7) y = 2 + 5 = 7
x = 2 , then y = 9 that means (2, 9) y = 4 + 5 = 9
x = 3 , then y = 11 that means (3,11) y = 6 + 5 = 11
x = 4 , then y = 13 that means (4, 13) y = 8 + 5 = 13
Represent the ratio relationship using a graph.
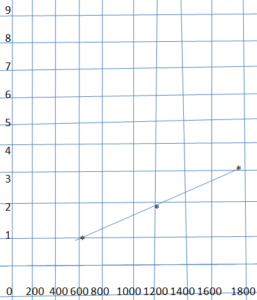
Question 4.
Answer:
1: 2 ratio
Explanation:
Question 5.
Answer:
1 : 2 ratio
Explanation:
Write the prime factorization of the number.
Question 6.
55
Answer:
5 . 11
Explanation:
5 x 11 = 55
S0 5,11
Question 7.
60
Answer:
2 x 2 x 3 x 5
Explanation:
2 x 30 = 60
2 x 15 = 30
5 x 3 = 15
3 x 1 = 3
Question 8.
150
Answer:
3 . 5 . 5 . 2
Explanation:
3 x 50 = 150
5 x 10 = 50
5 x 2 = 10
2 x 1 = 2
Question 9.
126
Answer:
2 . 3 . 3 . 7
Explanation:
2 x 63 = 126
3 x 21 = 63
3 x 7 = 21
7 x 1 = 7
Add or subtract.
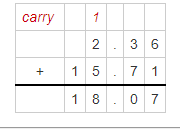
Question 10.
2.36 + 15.71
Answer:
2.36 + 15.71 = 18.07
Explanation:
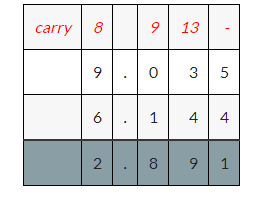
Question 11.
9.035 – 6.144
Answer:
9.035 – 6.144 = 2.891
Explanation:
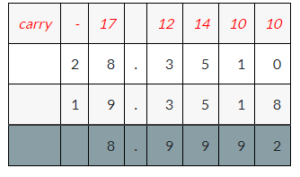
Question 12.
28.351 – 19.3518
Answer:
28.351 = 19.3518 = 8.9992
Explanation:
Concepts, Skills, & Problem Solving
USING TOOLS
Rearrange the parallelogram as a rectangle. Then find the area. (See Exploration 1, p. 285.)
Question 13.
Answer:

Question 14.
Answer:

Question 15.
Answer:

FINDING AREA
Find the area of the parallelogram.
Question 16.
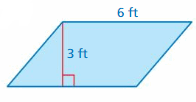
Answer:
The area of the parallelogram = 18 ft
Explanation:
The area of the parallelogram = the product of the base and the height
area = b x h given that base = 6 ft height = 3 ft
area = 18 ft
Question 17.
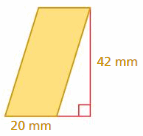
Answer:
The area of the parallelogram = 840 mm
Explanation:
The area of the parallelogram = the product of the base and the height
area = b x h given that base = 20 mm height = 42 ft
area = 840 mm
Question 18.
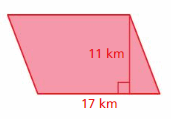
Answer:
The area of the parallelogram = 187 km
Explanation:
The area of the parallelogram = the product of the base and the height
area = b x h given that base = 17 km height = 11km
area = 187 km
Question 19.
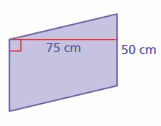
Answer:
The area of the parallelogram = 3750 cm
Explanation:
The area of the parallelogram = the product of the base and the height
area = b x h given that base = 75 cm height = 50 cm
area = 3750 cm
Question 20.
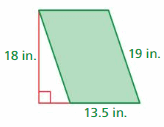
Answer:
The area of the parallelogram = 243 in
Explanation:
The area of the parallelogram = the product of the base and the height
area = b x h given that base = 13.5 in height = 18 in
area = 243 in
Question 21.
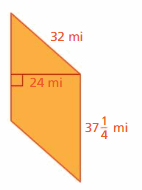
Answer:
The area of the parallelogram = 894 mi
Explanation:
The area of the parallelogram = the product of the base and the height
area = b x h given that base = 24 in, height = 37 x (1/4)
area = 24 x 37.25
area = 894 mi
Question 22.
YOU BE THE TEACHER
Your friend finds the area of the parallelogram. Is your friend correct? Explain your reasoning.
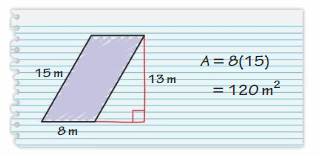
Answer:
Yes my friend is correct
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = 8 m x 15 m
Given that base = 8m and height = 15 m
area = base x height
area = 8 m x 15 m
area = 120 m
Question 23.
MODELING REAL LIFE
A ceramic tile in the shape of a parallelogram has a base of 4 inches and a height of 1.5 inches. What is the area of the tile?
Answer:
The area of the tile = 6 inches
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = base x height
area = 4 x 1.5
area = 6 inches
FINDING AREA
Find the area of the parallelogram. Round to the nearest hundredth if necessary.
Question 24.
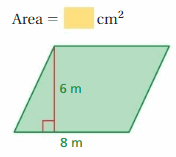
Answer:
4800 cm
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = base x height
area = 6 x 8
area = 48 m
1 meter = 100 centimeter
48 m = 4800 cm
Question 25.
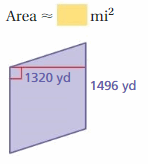
Answer:
1,121.64096
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = base x height
area = 1320 yd x 1496 yd
area = 1974720yd
1 yard = 0.000568 mile
1974720 yd = 1,121.64096 miles
Question 26.
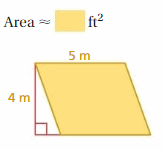
Answer:
67.4 ft
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = base x height
area = 5 m x 4 m
area = 20 m
1 meter = 3 feet 3.37 inches
20 m = 67 . 4 ft
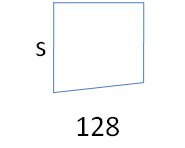
Question 27.
OPEN-ENDED
Your deck has an area of 128 square feet. After adding a section, the area will be (s2 + 128) square feet. Draw a diagram of how this can happen.
Answer:
Question 28.
MODELING REAL LIFE
You use the parallelogram-shaped sponge to create the T-shirt design. The area of the design is 66 square inches. How many times do you use the sponge to create the design? Draw a diagram to support your answer.
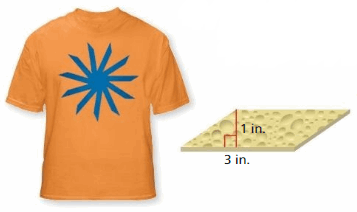
Answer:
33 times is used to the sponge to create the design = 33
Explanation:
The area of the parallelogram = base x height
area = 3 x 1
area = 3 inches
The area of the design = 66 inches
66/3 = 33
FINDING A MISSING DIMENSION
Find the missing dimension of the parallelogram described.
Question 29.
![]()
Answer:
height = 9 ft
Explanation:
area of the parallelogram = the product of the base and the product of the height
area = base x height
area = 6 ft x 9 ft
area = 54 ft
So height = 54
Question 30.
![]()
Answer:
base = 6.5 cm
Explanation:
area of the parallelogram = the product of the base and the product of the height
area = base x height
area = 6 . 5 cm x 2.5 cm
area = 16 .25
So height = 2.5 cm
Question 31.
![]()
Answer:
height = 4 yd
Explanation:
5(x + 4) = 5x + 20
Question 32.
DIG DEEPER!
The staircase has three identical parallelogram-shaped panels. The horizontal distance between each panel is 4.25 inches. The area of each panel is 287 square inches. What is the value of x?
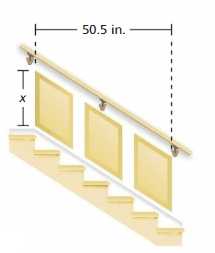
Answer:
The value of x = 14
Explanation:
(1/2)bx = 287
(1/2) x 14 x x = 287
7x = 287
x = 287/7
x = 41
50.5 -8
42.5 x 2 = 8.50
Question 33.
LOGIC
Each dimension of a parallelogram is multiplied by a positive number n. Write an expression for the area of the new parallelogram.
Answer:
The area of the parallelogram = (1/2) x b x h
area = (1/2)bn x hn
(1/2) bhn
Question 34.
CRITICAL THINKING
Rearrange the rhombus shown to write a formula for the area of a rhombus in terms of its diagonals.
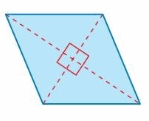
Answer:
The area of the rhombus = (1/2) ab
area = (1/2) x ab
Explanation:
The area of the rhombus = (1/2) ab
area = (1/2) x ab
Lesson 7.2 Areas of Triangles
EXPLORATION 1
Deriving the Area Formula of a Triangle
Work with a partner.
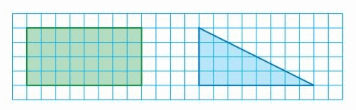
a. Draw any parallelogram on a piece of centimeter grid paper. Cut the parallelogram into two identical triangles. How can you use the area of the parallelogram to find the area of each triangle?
b. Copy the triangle below on a piece of centimeter grid paper. Find the area of the triangle. Explain how you found the area.
c. Draw any acute triangle on a piece of centimeter grid paper and find its area. Repeat this process for a right triangle and an obtuse triangle.
d. Do the areas change in part(c) when you use different sides as the base? Explain your reasoning.
Answer:
a : The area of the parallelogram = (1/2) x b x h
The area of the triangle = base x height
b : The area of the triangle = base x height
area = b x h
c : The area of the acute-angled triangle = (1/2) x b x h
The area of the right-angled triangle = (1/2) x base x perpendicular
The area of the obtuse-angled triangle =(1/2) x b x h
Explanation:
a : 
b : 
c :

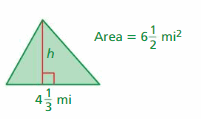
e. Use your results to write a formula for the area A of a triangle. Use the formula to find the area of the triangle shown.
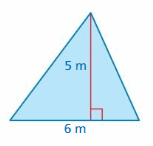
Answer:
15 m
Explanation:
The area of the triangle = half x the product of the base b and the product of the height h
area = (1/2) x b x h given that b= 6 m ,h = 5 m
area = (1/2) x 30
area = 15 m
7.2 Lesson
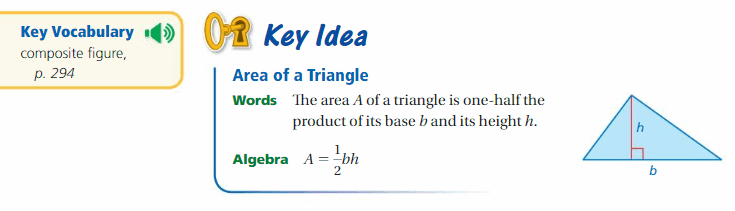
Try It
Find the area of the triangle
Question 1.
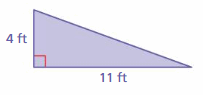
Answer:
22 ft
Explanation:
The area of the triangle = (1/2) x bh
The area of the triangle = (1/2) x the product of base and the product of the height
b = 11 ft , h = 4 ft
area = (1/2) x bh
area = (1/2) x 11 x 4
area = (1/2) x 44
area = 22 ft
Question 2.
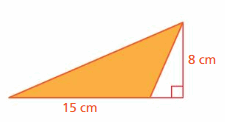
Answer:
Area = 60 cm
Explanation:
The area of the triangle = (1/2) x the product of the base b and the product of the height h
b = 15 cm, h = 8cm
area = (1/2) x 15 x 8
area = (1/2) x 120
area = 60
Question 3.
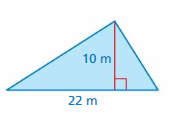
Answer:
area = 110 m
Explanation:
The area of the triangle = (1/2) x the product of the base b and the product of the height h
So the b = 22m ,h= 10 m
area= (1/2) x 10 x 22
area = (1/2) x 220
area = 110 m
Question 4.
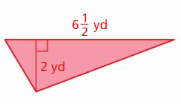
Answer:
6.5 yd
Explanation:
The area of the triangle = (1/2) x the product of base b and the product of the height h
So the b = (13/2) yd h = 2 yd
area = (1/2) x b x h
area = (1/2) x 6.5 x 2
area = (1/2) x 13
area = 6.5
Try It
Find the missing dimension of the triangle.
Question 5.
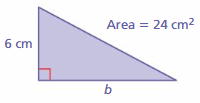
Answer:
Base = 8 cm
Explanation:
The area of the triangle =(1/2) x the product of the base b and the product of height h
area of the triangle = 24 cm given
So the height = 6cm given
area = (1/2) x b x h
area = (1/2) x 8 x 6
area = (1/2) x 48
area = 24
So base = 8 cm
Question 6.
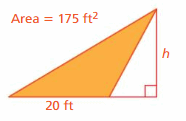
Answer:
height = 17.5ft
Explanation:
The area of the triangle =(1/2) x the product of the base b and the product of the height h
area of the triangle = 175 ft given,
So we have to find the height?
area = (1/2) x 20 x 17.5
area = (1/2) x 350
area = 175
So the height = 17.5 ft
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
FINDING AREA
Find the area of the triangle at the left.
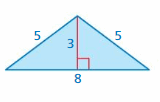
Answer:
The area of the triangle = 12
Explanation:
The area of the triangle = (1/2) x the product of base and the product of the height
b = 8 , h = 3
area = (1/2) x bh
area = (1/2) x 8 x 3
area = (1/2) x 24
area = 12
Question 8.
WRITING
Explain how to use the area of a parallelogram to find the area of a triangle.
Answer:
The area of the parallelogram = the product of the base and the product of the height
The area of the triangle = half x the product of the base b and the product of the height h
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = b x h
The area of the triangle = half x the product of the base and the height
area = (1/2) x b x h
FINDING A MISSING DIMENSION
Find the missing dimension of the triangle.
Question 9.
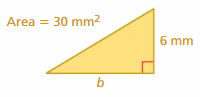
Answer:
base = 10 mm
Explanation:
The area of the triangle = (1/2) the product of the base and the product of the height
area = (1/2) x base x height
area = (1/2) x 10 mm x 6 mm
area = (1/2) x 60 mm
area = 30 mm
So base = 10 mm
Question 10.
A composite figure is made up of triangles, squares, rectangles, and other two-dimensional figures. To find the area of a composite figure, separate it into figures with areas you know how to find. This is called decomposition.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 11.
A wildlife conservation group buys the 9 square miles of land shown. What is the distance from Point A to Point B?
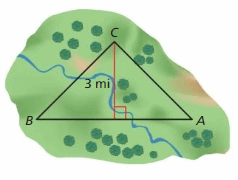
Answer:
The distance from point A to point B = 3 miles
Explanation:
The area of the triangle = (1/2) ab
Given that the land shown = 9 square miles
(1/2)bh = triangle ABC + triangle BCD
(3/2)b + (3/2)b = 9
(6/2)b = 9
3 b = 9
b = 3 miles
Question 12.
DIG DEEPER!
Find the area of the side of the chimney. Explain how you found the area.
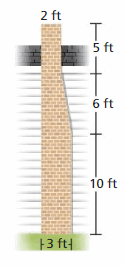
Answer:
The area of the chimney = 31.5 sq. ft
Explanation:
The area of the chimney = (1/2) x base x height
area = (1/2) x 3 x 21
area = 31.5 sq. ft
Areas of Triangles Homework & Practice 7.2
Review & Refresh
Find the area of the parallelogram.
Question 1.
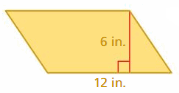
Answer:
The area of the parallelogram = 72 in
Explanation:
The area of the parallelogram = product of the height h and the product of the base b
b = 12 in, h = 6 in given
area = 12 x 6
area = 72 in
Question 2.
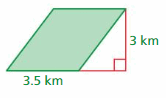
Answer:
The area of the parallelogram = 10.5 km
Explanation:
The area of the parallelogram = the product of the base b and the product of the height h
b = 3.5 km, h = 3km given
area = 3.5 x 3
area = 10.5 km
Question 3.
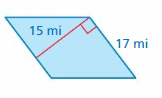
Answer:
The area of the parallelogram = 255 mi
Explanation:
The area of the parallelogram = the product of the base b and the product of the height h
b = 17 mi, h = 15 mi given
area = 17 x 15
area = 255 mi
Tell which property the statement illustrates.
Question 4.
n . 1 = n
Answer:
The product of x = the product of y
Explanation:
The product of x = n x 1 = n
the product of y = n
n = n
Question 5.
4 . m = m . 4
Answer:
The product of x = the product of y
Explanation:
The product of x = m x 4 = 4 m
the product of y = m x 4 = 4 m
4 . m = m . 4
Question 6.
(x + 2) + 5 = x + (2 + 5)
Answer:
The product of x = the product of y
Explanation:
The product of x = (x + 2) + 5
the product of y = x + (2 +5)
(x +2) +5 = x + (2 +5)
Question 7.
What is the first step when using order of operations?
A. Multiply and divide from left to right.
B. Add and subtract from left to right.
C. Perform operations in grouping symbols.
D. Evaluate numbers with exponents.
Answer:
Evaluate numbers with exponents
Concepts, Skills, & Problem Solving
USING TOOLS
Find the area of the triangle by forming a parallelogram. (See Exploration 1, p. 291.)
Question 8.
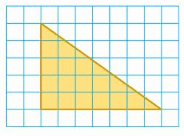
Answer:
The area of the right angled triangle = (1/2) x ab
Explanation:

Question 9.
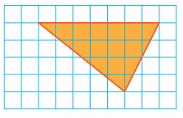
Answer:
obtused angled triangle = (1/2) x b xh
Explanation:

Question 10.
Answer:
acute angled triangle
Explanation:

FINDING AREA
Find the area of the triangle.
Question 11.
Answer:
The area of the triangle = 6 cm
Explanation:
Area of the triangle = (1/2) x the product of the base b and the product of the height h
area = (1/2) x b x h
So b = 3 cm , h = 4 cm
area = (1/2) x 3 x 4
area = (1/2) x 12
area = 6 cm
Question 12.
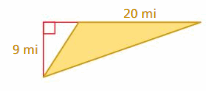
Answer:
The area of the triangle = 90 mi
Explanation:
Area of the triangle = (1/2) x the product of the base b and the product of the height h
area = (1/2) x b x h
So b = 20 mi , h = 9 mi
area = (1/2) x 20 x 9
area = (1/2) x 180
area = 90 sq. miles
Question 13.
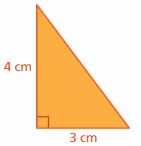
Answer:
The area of the triangle =1620 in
Explanation:
Area of the triangle = (1/2) x the product of the base b and the product of the height h
area = (1/2) x b x h
So b =60 in , h = 54 in
area = (1/2) x 3240
area = 1620 in
Question 14.
Answer:
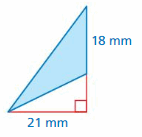
The area of the triangle = 189 mm
Explanation:
Area of the triangle = (1/2) x the product of the base b and the product of the height h
area = (1/2) x b x h
So b =21 mm , h = 18 mm
area = (1/2) x 378
area = 189 mm
Question 15.

Answer:
The area of the triangle = 1125 cm
Explanation:
Area of the triangle = (1/2) x the product of the base b and the product of the height h
area = (1/2) x b x h
So b =75 cm , h = 30 cm
area = (1/2) x 2250
area = 1125 cm
Question 16.
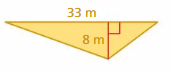
Answer:
The area of the triangle = 132 m
Explanation:
Area of the triangle = (1/2) x the product of the base b and the product of the height h
area = (1/2) x b x h
So b =8 m , h = 33 m
area = (1/2) x 264
area = 132 m
Question 17.
YOU BE THE TEACHER
Your friend finds the area of the triangle. Is your friend correct? Explain your reasoning.
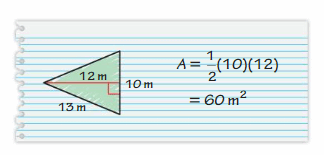
Answer:
Yes my friend is correct
Explanation:
Area of the triangle = (1/2) x the product of the base b and the product of the height h
area = (1/2) x b x h
Sob =10 m , h = 12 m
area = (1/2) x 120
area = 60 m
Question 18.
MODELING REAL LIFE
Estimate the area of the cottonwood leaf.
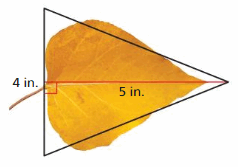
Answer:
The area of the cottonwood leaf = 10 in
Explanation:
Area of the triangle = (1/2) x the product of the base b and the product of the height h
area = (1/2) x b x h
Sob = 5 in , h = 4 in
area = (1/2) x 20
area = 10 in
Question 19.
MODELING REAL LIFE
A shelf has the shape of a triangle. The base of the shelf is 36 centimeters, and the height is 18 centimeters. Find the area of the shelf in square inches.
Answer:
The shape of the triangle = 324
Explanation:
Area of the triangle = (1/2) x the product of the base b and the product of the height h
area = (1/2) x b x h
Sob = 36 cm , h = 18 cm
area = (1/2) x 648
area = 324 sq. cm
Question 19.
FINDING A MISSING DIMENSION
Find the missing dimension of the triangle.
Question 20.
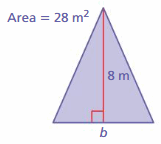
So base = 7 m
Question 21.
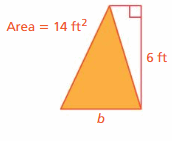
Answer:
Base of the triangle = 4.66 ft
Explanation:
The area of the triangle =(1/2) x the product of the base b and the product of height h
area of the triangle = 14 ft given
So the height = 6 ft given
area = (1/2) x b x h
area = (1/2) x 4.66 x 6
area = (1/2) x 27.96
area = 14
soo base = 4.66 ft
Question 22.
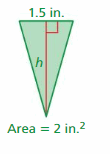
Answer:
Height = 2.66 in
Explanation:
The area of the triangle = (1/2) x the product of the base and the product of the height
area = (1/2) x 1.5 x h given that area = 2 in
2 = (1/2) x 1.5h
1.5 h = 4
h = (4/1.5)
h = 2.66 in
COMPOSITE FIGURES
Find the area of the figure.
Question 23.
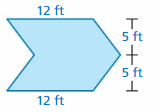
Answer:
The area of the figure = 44 ft
Explanation:
The area of the rectangle = 2 x(length + breadth)
area = 2 x (12 +10)
area = 2 x (22)
area = 44 sq. ft
Question 24.
Answer:
The area of the figure = 52 cm
Explanation:
The area of the rectangle = 2 x(length + breadth)
area = 2 x (11 +15)
area = 2 x (26)
area = 52 cm
Question 25.
Answer:
The area of the perimeter = 5/2 x a x b
Explanation:
The area of the perimeter = (5/2) x a x b
where a = middle point
b = sides
Question 26.
WRITING
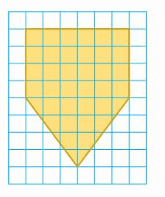
You know the height and the perimeter of an equilateral triangle. Explain how to find the area of the triangle. Draw a diagram to support your reasoning.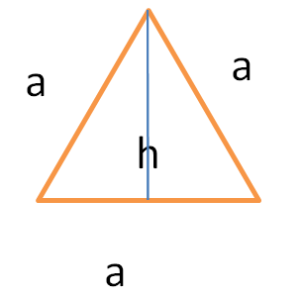
Answer:
The perimeter of the equilateral triangle = a x a x a = 3a
Explanation:
The perimeter of the equilateral triangle = 3a
height of the equilateral triangle = h
the area of the triangle = (1/2) x product of base b and the product of the height h
area = (1/2) x bh
Question 27.
CRITICAL THINKING
The total area of the polygon is 176 square feet. What is the value of x?
Answer:
The value of x = 6
Explanation:
The area of the polygon = 176 square feet given
area = 16 x 8 = 128
area = 176 – 128 = 48
The area of the right angle triangle = (a x b )/2
area = (8 x X)/2
48 = 4x + 4x
8x = 48
x = (48/8)
x = 6 ft
Question 28.
REASONING
The base and the height of Triangle A are one-half the base and the height of Triangle B. How many times greater is the area of Triangle B?
Answer:
2 times
Explanation:
The triangle B is 2 times greater than the triangle A
Question 29.
STRUCTURE
Use what you know about finding areas of triangles to write a formula for the area of a rhombus in terms of its diagonals. Compare the formula with your answer to Section 7.1 Exercise 34.
Answer:
The area of the triangle = (1/2) ab
The area of the rhombus = (1/2) ab
Explanation:
The area of the triangle is equal to the area of the rhombus
area of the triangle = (1/2) ab
area of the rhombus = (1/2) ab
Lesson 7.3 Areas of Trapezoids and Kites
EXPLORATION 1
Deriving the Area Formula of a Trapezoid
Work with a partner.
a. Draw any parallelogram on a piece of centimeter grid paper. Cut the parallelogram into two identical trapezoids. How can you use the area of the parallelogram to find the area of each trapezoid?
b. Copy the trapezoid below on a piece of centimeter grid paper. Find the area of the trapezoid. Explain how you found the area.
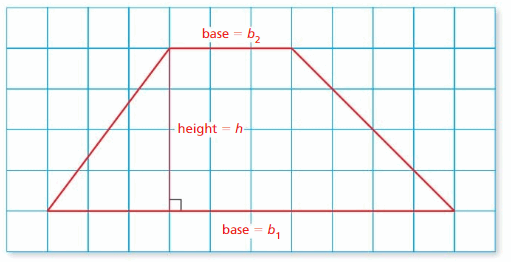
c. Draw any trapezoid on a piece of centimeter grid paper and find its area.
d. Use your results to write a formula for the area A of a trapezoid. Use the formula to find the area of the trapezoid shown.

7.3 Lesson
You can use decomposition to find areas of trapezoids and kites. A kite is a quadrilateral that has two pairs of adjacent sides with the same length and opposite sides with different lengths.
Try It
Find the area of the figure.
Question 1.
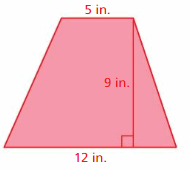
Answer:
76.5 in
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (5 + 12). Given that b1 = 5 and b2 = 12
area = (1/2) x 9(17) given that h = 9
area = (1/2) x 153
area = 76.5 sq. in
Question 2.
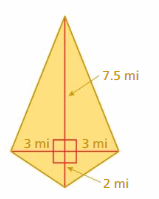
Answer:
65.45 sq. mi
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (3 + 3). Given that b1 = 3 and b2 = 3
area = (1/2) x 7.7(17) given that h = 7.7
area = (1/2) x 130.9
area = 65.45 sq. mi
In Example 1(a), you could have used a copy of the trapezoid to form a parallelogram. As you may have discovered in the exploration, this leads to the following formula for the area of a trapezoid.
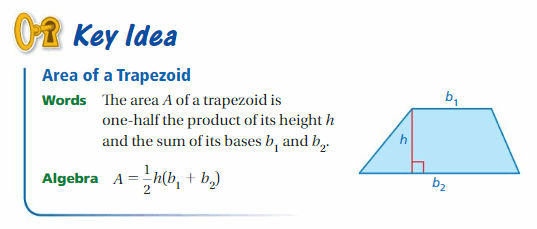
Try It
Find the area of the trapezoid.
Question 3.
Answer:
The area of the trapezoid = 22.5 sq. mm
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (5 + 4). Given that b1 = 5 and b2 = 4
area = (1/2) x 8(9) given that h = 8
area = (1/2) x 45
area = 22.5 sq. mm
Question 4.
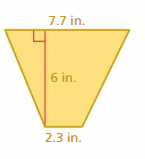
Answer:
The area of the trapezoid = 30 sq. in
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (7.7 + 2.3). Given that b1 = 7.7 and b2 = 2.3
area = (1/2) x 6(10) given that h = 6 in
area = (1/2) x 60
area = 30 sq. in
Try It
Find the area of the figure.
Question 5.
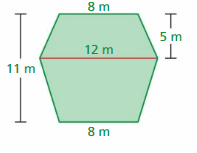
Answer:
The area of the trapezoid1 = 60 sq. m
The area of the trapezoid2= 88 sq. m
Explanation:
The area of the trapezoid1 = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (5 + 5). Given that b1 = 5 and b2 = 5
area = (1/2) x 12(10) given that h = 6 m
area = (1/2) x 120
area = 60 sq. m
The area of the trapezoid2 = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (8 + 8). Given that b1 = 8 and b2 = 8
area = (1/2) x 11(16) given that h = 6 m
area = 88 sq. m
Question 6.
Answer:
The area of the trapezoid = 112 sq. in
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (6+ 10). Given that b1 = 6 and b2 = 10
area = (1/2) x 14(16) given that h = 14 in
area = (1/2) x 224
area = 112 sq. in
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
WRITING
Explain how to use the area of a parallelogram to find the area of a trapezoid.
Answer:
The area of the parallelogram = product of the height h and the product of the base b
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
Question 8.
REASONING
What measures do you need to find the area of a kite?
Answer:
Rhombus is used to find the area of the kite
Explanation:
The area of the rhombus = (1/2) x side x height
area = (1/2) x s x h
area = (1/2) sh
kite is also same as the rhombus
FINDING AREA
Find the area of the figure.
Question 9.
Answer:
Area = 52.5 sq. yd
Explanation:
The area of the trapezoid = (1/2) x height x the product of the base 1 and the base 2
area = (1/2) x height x (b1 + b2)
area = (1/2) x 5 x (9 + 12)
area = (1/2) x 5 x 21
area = (1/2) x 105
area = 52.5 sq. yd
Question 10.
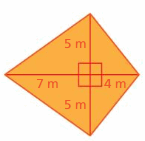
Answer:
Area = 55 sq. m
Explanation:
The area of the trapezoid = (1/2) x height x the product of the base 1 and the base 2
area = (1/2) x height x (b1 + b2)
area = (1/2) x 10 x (7 + 4)
area = (1/2) x 10x 11
area = (1/2) x 110
area = 55 sq. m
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 11.
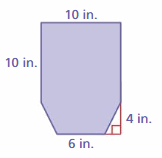
DIG DEEPER!
An archaeologist estimates that the manuscript shown was originally a rectangle with a length of 20 inches. Estimate the area of the fragment that is missing.
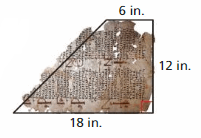
Answer:
144 square inches
Explanation:
The area of the right angle triangle = a x b where a = height b = base
area = a x b a=12 b = 18 – 6 = 12
area = 12 x 12
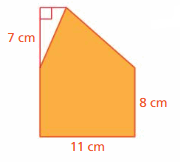
area = 144 sq. in
Question 12.
The stained-glass window is made of identical kite-shaped glass panes. The approximate dimensions of one pane are shown. The glass used to make the window costs $12.50 per square foot. Find the total cost of the glass used to make the window.
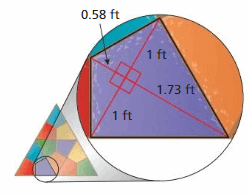
Answer:
The total cost of the glass used to make the window is 14.4375 $
Explanation:
The area of the rhombus = (1/2) x the product of the side s and the product of height h
area = (1/2) x2 ft x 2.31ft
area = ( 4.62/2)
Area = 2.31 x 12.50$
area = 14.4375$
Areas of Trapezoids and Kites Homework & Practice 7.3
Review & Refresh
Find the area of the triangle.
Question 1.
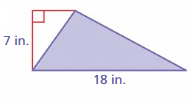
Answer:
Area =63 in
Explanation:
The area of the triangle = half the product of the base and the product of the height
area = (1/2)bh
area = (1/2) x 18 x 7
area = (126/2)
area = 63 in
Question 2.
Answer:
Area =26 sq. km
Explanation:
The area of the triangle = half the product of the base and the product of the height
area = (1/2)bh
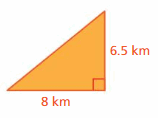
area = (1/2) x 8 x 6.5
area = (52/2)
area = 26 sq. km
Question 3.
Answer:
Area =25 sq. ft
Explanation:
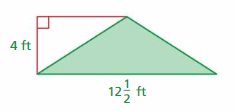
The area of the triangle = half the product of the base and the product of the height
area = (1/2)bh
area = (1/2) x 4 x 12.5
area = (50/2)
area = 25 sq. ft
Classify the quadrilateral./
Question 4.

Answer:
The above quadrilateral look similar to the rectangle
Explanation:
Rectangle
the area of the rectangle = length x width
area = l x w
Question 5.
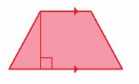
Answer:
The above diagram is similar to the trapezoid
Explanation:
The area of the trapezoid = half the product of the base and the product of the height
area = (1/2) x b x h
Question 6.
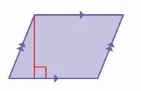
Answer:
The above figure is similar to the parallelogram
Explanation:
The area of the parallelogram = the product of the height and the product of the base b
area = b x h
Question 7.
On a normal day, 12 airplanes arrive at an airport every 15 minutes. Which rate does not represent this situation?
A. 24 airplanes every 30 minutes
B. 4 airplanes every 5 minutes
C. 6 airplanes every 5 minutes
D. 48 airplanes each hour
Answer:
B
Explanation:
4 airplanes every 5 minutes
Concepts, Skills, & Problem Solving
USING TOOLS
Find the area of the trapezoid by forming a parallelogram. (See Exploration 1, p. 297.)
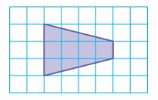
Question 8.
Answer:
The area of the trapezoid = (1/2) x b x l x h
Explanation:
The area of the trapezoid = (1/2) x b x l x h
area = (1/2) x b x h x l
area = (lxb/2)x h
Question 9.
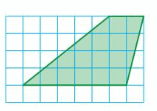
Answer:
The area of the trapezoid = (1/2) x b x l x h
Explanation:
The area of the trapezoid = (1/2) x b x l x h
area = (1/2) x b x h x l
area = (lxb/2)x h
Question 10.
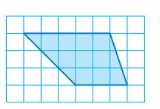
Answer:
The area of the trapezoid = (1/2) x b x l x h
Explanation:
The area of the trapezoid = (1/2) x b x l x h
area = (1/2) x b x h x l
area = (lxb/2)x h
FINDING AREA
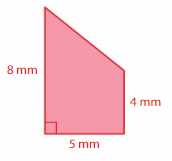
Use decomposition to find the area of the figure.
Question 11.
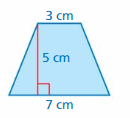
Answer:
25 cm
Explanation:
The area of the triangle = (1/2) b x h
base value = 2, height = 5 given
area = (1/2) x 5 x 2
area = 5
the area of another triangle = 5
the remaining = rectangle
area of rectangle = length x breadth
area = 15 + 5 + 5 = 25 cm
Question 12.
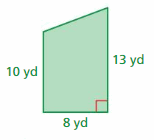
Answer:
92 sq. yd
Explanation:
The area of the triangle = (1/2) b x h
base value = 2, height = 5 given
area = (1/2) x 8 x 2=3
area = 12
the remaining = rectangle
area of rectangle = length x breadth
area = 80 + 12 yd
area = 92 yd
Question 13.
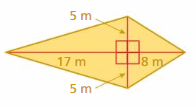
Answer:
125 m
Explanation:
The area of the triangle = (1/2) b x h
base value = 2, height = 5 given
area = (1/2) x 8 x 5= 20
area = 20
The area of the triangle = (1/2) b x h
base value = 17, height = 5 given
area = (1/2) x 17 x 5= 20
area = 42.5
area = 20 + 20+ 42.5 + 42.5
area = 125 m
Question 14.
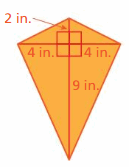
Answer:
The area of the figure = 44 inches
Explanation:
The area of the triangle = (1/2) b x h
base value = 9, height = 4 given
area = (1/2) x 9 x 4= 18
area = 18
the remaining = rectangle
area of rectangle = length x breadth
area = 18 + 18 + 4 +
area = 44 inches
Question 15.
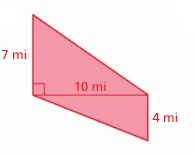
Answer:
The area of the figure = 55 miles
Explanation:
The area of the triangle = (1/2) b x h
base value = 10, height = 7 given
area = (1/2) x 10 x 7= 35
area = 35 mi
The area of the triangle = (1/2) b x h
base value = 10, height = 4 given
area = (1/2) x 10 x 4= 20
area = 20 mi
area = 20 + 35 = 55
area = 55 mi
Question 16.
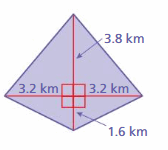
Answer:
The area of the figure = 17.68 miles
Explanation:
The area of the triangle = (1/2) b x h
base value = 3.2, height = 3.8 given
area = (1/2) x 3.2 x 3.8= 35
area = 6.08
The area of the triangle = (1/2) b x h
base value = 3.2, height = 1.6given
area = (1/2) x 3.2 x 1.6= 20
area = 2.56
area = 2.56 + 2.56 + 6.08 + 6.08 = 17.68 kms
area = 17.68 miles
FINDING AREA
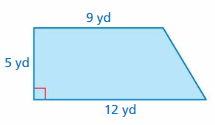
Find the area of the trapezoid.
Question 17.
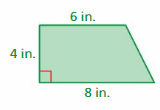
Answer:
28 in
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (b1 +b2)
area = (1/2) x 4 x (6 + 8)/
area = (1/2) x 4 x 14
area = 28 sq. in
Question 18.
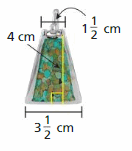
Answer:
10 sq. cm
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (b1 +b2)
area = (1/2) x 4 x (3.5 + 1.5)
area = (1/2) x 4 x 5
area = 10 sq. cm
Question 19.
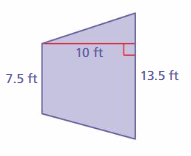
Answer:
105 sq. ft
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (b1 +b2)
area = (1/2) x 10 x (13.5 + 7.5)
area = (1/2) x 10 x 21
area = 105 sq. ft
Question 20.
YOU BE THE TEACHER
Your friend finds the area of the trapezoid. Is your friend correct? Explain your reasoning.
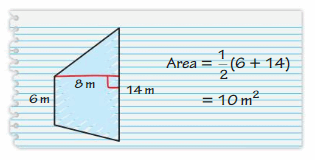
Answer:
No my friend is not correct
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (b1 +b2)
area = (1/2) x 8 x (6 +14)
area = (1/2) x 160
area = 80 sq. m
Question 21.
MODELING REAL LIFE
Light shines through a window. What is the area of the trapezoid-shaped region created by the light?
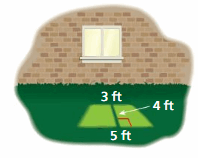
Answer:
16 sq. ft
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (b1 +b2) given that b1 = 3 and b2 = 5
area = (1/2) x 4 x (5 +3)
area = (1/2) x 32
area = 16 sq. ft
COMPOSITE FIGURES
Find the area of the figure.
Question 22.
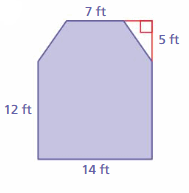
Answer:
178.5 sq. ft
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (14 +7) given that b1 = 14 and b2 = 7
area = (1/2) x 17 x (14 +7)
area = (1/2) x 357
area = 178.5 sq. ft
Question 23.
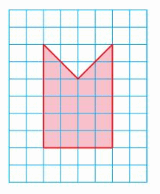
Question 24.
FINDING A MISSING DIMENSION
Find the height of the trapezoid.
Question 25.
Answer:
The height of the trapezoid = square root of height and bases
Question 26.
Question 27.
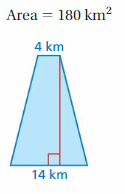
FINDING AREA
Find the area (in square feet) of a trapezoid with height hand bases b1 and b2.
Question 28.
h = 6 in.
b1 = 9 in.
b2 = 12 in.
Answer:
The area of the trapezoid = 0.43722 square feet
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (9 +12) given that b1 = 9 and b2 = 12
area = (1/2) x 6 x (9 + 12)
area = (1/2) x 126
area = 63 in
1 inch = 0.00694 sq feet
so 0.43722sq ft
Question 29.
h = 12 yd
b1 = 5 yd
b2 = 7 yd
Answer:
The area of the trapezoid = 648 square feet
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (5 +7) given that b1 = 5 and b2 = 7
area = (1/2) x 12 x (5 + 7)
area = (1/2) x 144
area =72 yd
1 yard = 9 sq feet
so 72 yd = 72 x 9 sq ft
area = 648 sq ft
Question 30.
h = 6 m
b1 = 3 m
b2 = 8 m
Answer:
The area of the trapezoid = 355.212 square feet
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (3 +8) given that b1 = 3 and b2 = 8
area = (1/2) x 6 x (3 + 8)
area = (1/2) x 66
area =33 m
1 m = 10.764 sq feet
so 33 m = 33 x 10.764sq ft
area = 355.212 sq ft
Question 31.
OPEN-ENDED
The area of the trapezoidal student election sign is 5 square feet. Find two possible values for each base length.

Answer:
The area of the trapezoid = 4 ft
Explanation:
Area of trapezoid = half the product of the height and the product of the bases
area = (1/2) x h x (4 +4) given that b1 = 4 and b2 = 4
area = (1/2) x 2 x (4 + 4)
area = (1/2) x 8
area = 4 sq. ft
Question 32.
REASONING
How many times greater is the area of the floor covered by the larger speaker than by the smaller speaker?

Answer:
2 times
Explanation:
The larger speaker is 2 times greater than that of the smaller speaker
Question 33.
REASONING
The rectangle and the trapezoid have the same area. What is the length ℓ of the rectangle?
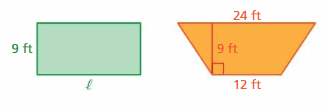
Question 34.
Answer:
The area of the triangle =36
Explanation:
In the above given trapezoid the bases b1 = 12 and b2 = 24 height = 9 ft
So the area of the trapezoid = (1/2) x h x(b1 + b2)
area = (1/2) x 9 x (12 +24)
area = (1/2) x 324
area = 162
The length of the triangle = length X w
162 = 9l
length = 36 ft
CRITICAL THINKING
In the figureshown, the area of the trapezoid is less than twice the area of the triangle. Find the possible values of x. Can the trapezoid have the same area as the triangle? Explain your reasoning.
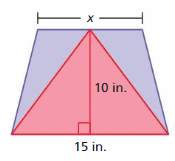
Answer:
The possible value of x = 15 in
Explanation:
In the above statement they said that the area of the trapezoid is less than twice the area of the triangle
area of the triangle = (1/2) x b x h
area = (1/2) x 15 x 10
area = (150/2) =75
Area of trapezoid = (1/2) x h x (b1 + b2)
area = (1/2) x 10 x (15 +15)
area = (300/2)
area = 150
So the area of the trapezoid is 2 times less than the area of the triangle.
Question 35.
STRUCTURE
In Section 7.1 Exercise 34 and Section 7.2 Exercise 29, you wrote a formula for the area of a rhombus in terms of its diagonals.
a. Use what you know about finding areas of figures to write a formula for the area of a kite in terms of its diagonals.
b. Are there any similarities between your formula in part(a) and the formula you found in Sections 7.1 and 7.2? Explain why or why not.
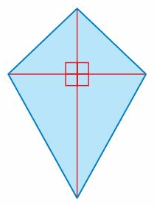
Answer:
The area of the rhombus = (1/2) x side x height
Explanation:
The kite is looking the same as the rhombus
area of the rhombus = (1/2) x side x height
Lesson 7.4 Three-Dimensional Figures
EXPLORATION 1
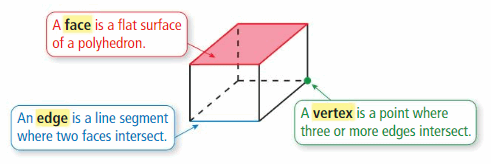
Exploring Faces, Edges and Vertices
Work with a partner. Use the rectangular prism shown.
a. Prisms have faces, edges, and vertices. What does each of these terms mean?
b. What does it mean for lines or planes to be parallel or perpendicular in three dimensions? Use drawings to identify one pair of each of the following.
- parallel faces
- parallel edges
- edge parallel to a face
- perpendicular faces
- perpendicular edges
- edge perpendicular to a face

EXPLORATION 2
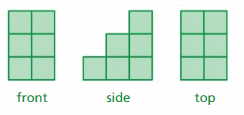
Drawing Views of a Solid
Work with a partner. Draw the front, side, and top views of each stack of cubes. Then find the number of cubes in the stack. An example is shown at the left.
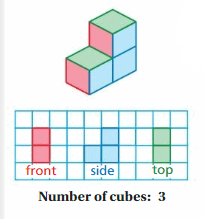
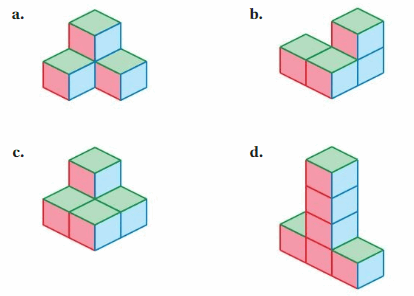
Answer:
a: the number of cubes = 4
b: the number of cubes = 4
c: the number of cubes = 5
d: the number of cubes = 6
Explanation:
a:
b::
c:
d:
7.4 Lesson
A solid is a three-dimensional figure that encloses a space. A polyhedron is a solid whose faces are all polygons.
Try It
Question 1.
Find the numbers of faces, edges, and vertices of the solid.
Answer:
faces = 5
edges = 12
vertices = 6
Explanation:
The number of faces = 5
the number of edges = 12
the number of vertices = 6
Key Ideas
Try It
Draw the solid.
Question 2.
square prism
Answer:
Question 3.
pentagonal pyramid
Answer:
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
FACES, EDGES, AND VERTICES
Find the numbers of faces, edges, and vertices of the solid at the left.
Answer:
faces : 3
edges : 6
vertices : 3
Explanation:
The number of faces of solid at the left = 3
edges = 6
vertices = 3
Question 5.
DRAWING A SOLID
Draw an octagonal prism.
Answer:
Question 6.
WHICH ONE DOESN’T BELONG?
Which figuredoes not belong with the other three? Explain your reasoning.
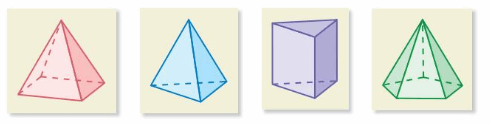
Answer:
The 3rd figure is different from the other 3 figures
Explanation:
The 3rd figure is the same as the square prism
the other 3 figures are triangular prisms
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
The Flatiron Building in New York City is in the shape of a triangular prism. Draw a sketch of the building.

Answer:
Question 8.
The Pyramid of the Niches is in El Tajín, an archaeological site in Veracruz, Mexico. Draw the front, side, and top views of the pyramid. Explain.

Answer:
Front = 2
side = 1
top = 1
Explanation:

Question 9.
Use the point-cut diamond shown.
a. Find the numbers of faces, edges, and vertices of the diamond.
b. Draw the front, side, and top views of the diamond.
c. How can a jeweler transform the point-cut diamond into a table-cut diamond as in Example 3?
Answer:
a : the number of faces = 8,edges = 16,vertices = 6
b : front = 2 , side = 2,top = 1
Explanation:
a : faces = 8
edges = 16
vertices = 6
b : ![]()
Three-Dimensional Figures Homework & Practice 7.4
Review & Refresh
Find the area of the figure.
Question 1.
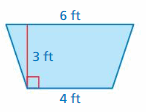
Answer:
The area of the triangle = 15 ft
Explanation:
In the above given trapezoid the bases b1 = 12 and b2 = 24 height = 9 ft
So the area of the trapezoid = (1/2) x h x(b1 + b2)
area = (1/2) x 3 x (4 +6)
area = (1/2) x 30
area = 15
Question 2.
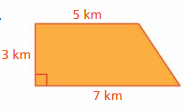
Answer:
The area of the triangle = 18 km
Explanation:
In the above given trapezoid the bases b1 = 12 and b2 = 24 height = 9 ft
So the area of the trapezoid = (1/2) x h x(b1 + b2)
area = (1/2) x 3 x (5 +7)
area = (1/2) x 36
area = 18 km
Question 3.
Answer:
The area of the triangle = 18 km
Explanation:
In the above given trapezoid the bases b1 = 12 and b2 = 24 height = 9 ft
So the area of the trapezoid = (1/2) x h x(b1 + b2)
area = (1/2) x 18 x (6 +6)
area = (1/2) x 216
area = 18 k
Find the LCM of the numbers.
Question 4.
8, 12
Answer:
24
Explanation:
Factors of 8 = 2 x 2 x2
factors of 12 = 2 x 2x 3
l.c.m. = 2 x 2 x 2x 3
l.c.m = 24
Question 5.
15, 25
Answer:
75
Explanation:
Factors of 15 = 5 x 3
factors of 25 = 5 x 5
l.c.m. = 5 x 3 x5
l.c.m = 75
Question 6.
32, 44
Answer:
352
Explanation:
Factors of 32 = 8 x 4
factors of 44 = 11 x 4
l.c.m. = 4 x 11 x 8
l.c.m = 352
Question 7.
3, 7, 10
Answer:
210
Explanation:
Factors of 3 = 3 x 1
factors of 7 = 7 x 1
factors of 10 =5 x 2
l.c.m. = 3 x 7 x 5 x 2
l.c.m = 210
A bucket contains stones and seashells. You are given the number of seashells in the bucket and the ratio of stones to seashells. Find the number of stones in the bucket.
Question 8.
18 seashells; 2 to 1
Answer:
No of stones = 12
No of seashells = 6
Explanation:
(18/3) = 6
2 : 1 = 12 : 6
Question 9.
30 seashells; 4 : 3
Answer:
No of stones = 17.14
No of seashells = 12.6
Explanation:
(30/7) = 4.2
4 : 3 = 17.4 : 12.6
Question 10.
40 seashells; 7 : 4
Answer:
No of stones = 25.45
No of seashells = 14.54
Explanation:
(40/11) = 3.63
7 : 4 = 25.45 : 14.54
Concepts, Skills, & Problem Solving
DRAWING VIEWS OF A SOLID
Draw the front, side, and top views of the stack of cubes. Then find the number of cubes in the stack. (See Exploration 2, p. 305.)
Question 11.
Answer:
front = 10
side = 3
top = 4
Explanation:
Question 12.
Answer:
front = 9
side = 3
top = 5
Explanation:
Question 13.
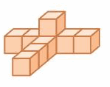
Answer:
front = 5
side = 5
top = 8
Explanation:
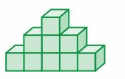
FACES, EDGES, AND VERTICES
Find the numbers of faces, edges, and vertices of the solid.
Question 14.
Answer:
faces = 10
edges = 24
vertices = 9
Explanation:
The number of faces = 10
the number of edges = 24
the number of vertices =9
Question 15.
Answer:
faces = 17
edges = 34
vertices = 13
Explanation:
The number of faces = 17
the number of edges = 34
the number of vertices =13
Question 16.
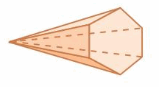
Answer:
faces = 10
edges = 20
vertices = 7
Explanation:
The number of faces = 10
the number of edges = 20
the number of vertices =7
DRAWING SOLIDS
Draw the solid.
Question 17.
triangular prism
Answer:
Question 18.
pentagonal prism
Answer:
Question 19.
rectangular pyramid
Question 20.
hexagonal pyramid
Answer:
Question 21.
MODELING REAL LIFE
The Pyramid of Cestius in Rome, Italy, is in the shape of a square pyramid. Draw a sketch of the pyramid.

Answer:
Question 22.
RESEARCH
Use the Internet to find a picture of the Washington Monument. Describe its shape.
DRAWING VIEWS OF A SOLID
Draw the front, side, and top views of the solid.
Question 23.

Answer:
front = 1
side = 2
top = 1
Explanation:

Question 24.
Answer:
front =2
side = 2
top = 1
Explanation:
Question 25.
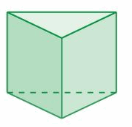
Answer:
front =2
side = 2
top = 1
Explanation:

Question 26.
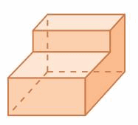
Answer:
front =2
side = 2
top = 2
Explanation:

Question 27.

Answer:
front = 1
side = 2
top = 1
Explanation:

Question 28.
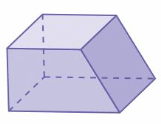
Answer:
front = 1
side = 1
top = 1
Explanation:

DRAWING SOLIDS
Draw a solid with the following front, side, and top views.
Question 29.
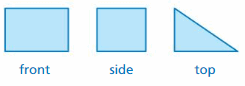
Answer:
Explanation:
front = 2 top = 1 side = 2
Question 30.
Question 31.
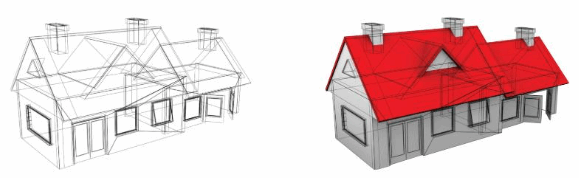
MODELING REAL LIFE
Design and draw a house. Name the different solids that you can use to make a model of the house.
Question 32.
DIG DEEPER!
Two of the three views of a solid are shown.
a. What is the greatest number of cubes in the solid?
b. What is the least number of cubes in the solid?
c. Draw the front views of both solids in parts (a) and (b).
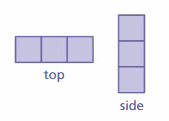
Answer:
a: The greatest number of cubes in the solid = 3
b : The least number of cubes in the solid = 2
c : 
Question 33.
OPEN-ENDED
Draw two different solids with five faces.
a. Write the numbers of vertices and edges for each solid.
b. Explain how knowing the numbers of edges and vertices helps you draw a three-dimensional figure.
Question 34.
CRITICAL THINKING
The base of a pyramid has n sides. Find the numbers of faces, edges, and vertices of the pyramid. Explain your reasoning.
Lesson 7.5 Surface Areas of Prisms
EXPLORATION 1
Using Grid Paper to Construct a Solid
Work with a partner. Copy the figure shown below onto grid paper.

a. Cut out and fold the figure to form a solid. What type of solid does the figure form?
b. What is the area of the entire surface of the solid?
EXPLORATION 2
Finding the Area of the Entire Surface
Work with a partner. Find the area of the entire surface of each solid. Explain your reasoning.

Answer:

7.5 Lesson
The surface area of a solid is the sum of the areas of all of its faces. You can use a two-dimensional representation of a solid, called a net, to find the surface area of the solid. Surface area is measured in square units.

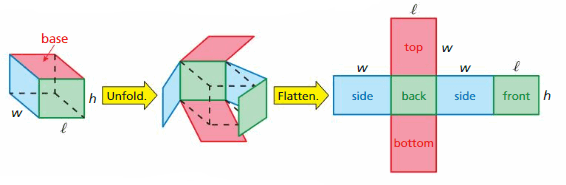
Key Idea
Net of a Rectangular Prism
A rectangular prism is a prism with rectangular bases.
Try It
Find the surface area of the rectangular prism.
Question 1.
Answer:
258 sq. m
Explanation:
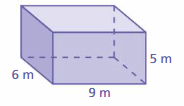
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 9 x 5 + 9 x 5 + 6 x 9+ 6 x 9 + 6 x 5 +6 x 5
surface area = 45 + 45 + 54 + 54 + 30 +30
surface area = 258 sq. mm
Question 2.
Answer:
286 sq. ft
Explanation:
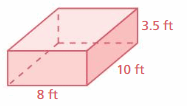
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 10 x 3.5 + 10 x 3.5 + 10 x 8+ 10 x 8 + 8 x 3.5 + 8 x 3.5
surface area = 35 +35+ 80 + 80 +28 +28
surface area = 286 sq. ft
Key Idea
Net of a Triangular Prism
A triangular prism is a prism with triangular bases.
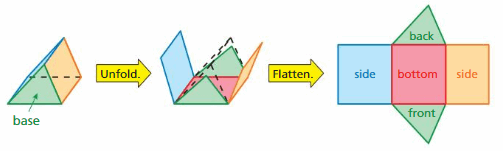
Try It
Find the surface area of the triangular prism.
Question 3.
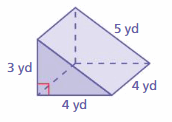
Answer:
67 sq. yd
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 3 x 5 = 15+ (1/2) x 3 x 4 = 6 + (1/2) x 3 x 4 = 6 + 4 x 5 = 20 + 5 x 4 = 20
bottom = 3 x 5 , front = (1/2) x 3 x 4, back = (1/2) x 3 x 4, side = 4 x 5 , side = 5 x 4
surface area = 15 +6 +6 +20 + 20
area = 67 sq. yd
Question 4.
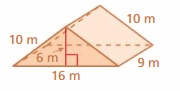
Answer:
510 sq. m
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 10 x 10 = 100+ (1/2) x 10 x 16=80 + (1/2) x 10 x 16 = 80+ 9 x 10 =90 + 10 x 16=160
bottom = 10 x 10 , front = (1/2) x 10 x 16, back = (1/2) x 10 x 16, side = 9 x 10 , side = 10 x 16
surface area = 100 +80 +80+90 +160
area = 510 sq. m
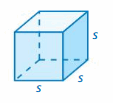
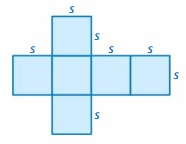
When all the edges of a rectangular prism have the same length s, the rectangular prism is a cube. The net of a cube shows that each of the 6 identical square faces has an area of s2. So, a formula for the surface area of a cube is
S = 6s2. Formula for surface area of a cube
Try It
Find the surface area of the cube.
Question 5.
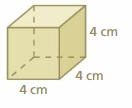
Answer:
96 sq. cm
Explanation:
area of the cube = 6 s2
area = 6 x side x side
area = 6 x 4 x 4
area = 96 sq. cm
Question 6.
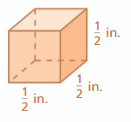
Answer:
1.5 sq. in
Explanation:
area of the cube = 6 s2
area = 6 x side x side
area = 6 x 0.5 x 0.5
area = 1.5 sq. in
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
FINDING SURFACE AREA
Find the surface area of a cube with edge lengths of 9 centimeters.
Answer:
486 sq. cm
Explanation:
area of the cube = 6 s2
area = 6 x side x side given that s = 9 cm
area = 6 x 9 x 9
area = 486 sq. cm
Question 8.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
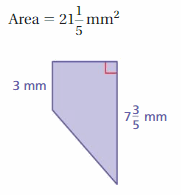
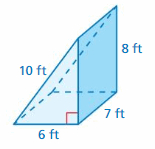
Question 9.
Light shines through a glass prism and forms a rainbow. What is the surface area of the prism?
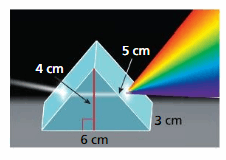
Answer:
93 sq. cm
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 6 x 3 = 18+ (1/2) x 5 x 6=30 + (1/2) x 5 x 6 = 30+ 3 x 5 =15+ 5 x 6= 30
bottom = 6 x 3 , front = (1/2) x 5 x 6, back = (1/2) x 5 x 6, side = 3 x 5 , side = 5 x 6
surface area = 18 +15 +15 +15 +30
area = 93 sq. cm
Question 10.
One pint of chalkboard paint covers 60 square feet. What is the least number of pints of paint needed to paint the walls of a room in the shape of a rectangular prism with a length of 15 feet, a width of 13 feet, and a height of 10 feet? Explain.
Question 11.
DIG DEEPER!
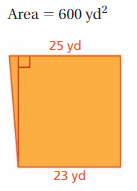
A flexible metamaterial is developed for use in robotics and prosthetics. A block of metamaterial is in the shape of a cube with a surface area of 600 square centimeters. What is the edge length of the block of metamaterial?
Answer:
The edge length of the block of metamaterial = 25 square centimeters
Explanation:
The surface area of the cube = 6 s square
area = 6 x 25 x4
area = 6 x100
area = 600 square centimeters
Surface Areas of Prisms Homework & Practice 7.5
Review & Refresh
Draw the front, side, and top views of the solid.
Question 1.
Answer:
front = 1
side = 2
top = 1
Explanation:

Question 2.
Answer:
front = 1
side = 1
top = 1
Explanation:

Question 3.
Answer:
front = 1
side = 2
top = 2
Explanation:

Find the GCF of the numbers.
Question 4.
18, 72
Answer:
18
Explanation:
The factors of 18 are = 3 x 3 x 2
The factors of 72 are = 3 x 3 x 2 x 2 x 2
From the above the greatest common factors are = 3 x 3 x 2 =18
Question 5.
44, 110
Answer:
22
Explanation:
The factors of 44 are = 2 x 2 x 11
The factors of 110 are = 2 x 5 x 11
From the above the greatest common factors are = 2 x 11 = 22
Question 6.
78, 93
Answer:
3
Explanation:
The factors of 78 are = 2 x 3 x 13
The factors of 93 are = 3 x 31
From the above the greatest common factors are = 3
Question 7.
60, 96, 156
Answer :
12
Explanation:
The factors of 60 are = 2 x 2 x 3 x5
The factors of 96 are = 2 x 2 x 2x 2 x 2 x 3
The factors of 156 are =2 x 2 x 3 x 13
From the above the greatest common factors are = 2 x 2 x 3 = 12
Solve the equation.
Question 8.
s – 5 = 12
Answer:
17
Explanation:
s = 12 + 5
s = 17
Question 9.
x + 9 = 20
Answer:
11
Explanation:
x = 20 -9
x = 11
Question 10.
48 = 6r
Answer:
r = 8
Explanation:
48 = 6r
r = (48/6)
r = 8
Question 11.
\(\frac{m}{5}\) = 13
Answer:
65
Explanation:
(m/5) = 13
m = 13 x 5
m = 65
Divide.
Question 12.
496 ÷ 16
Answer:
31
Explanation:
(496/16) = 31
Question 13.
765 ÷ 45
Answer:
17
Explanation:
(765/45) = 17
Question 14.
1173 ÷ 23
Answer:
51
Explanation:
(1173/23) = 51
Concepts, Skills, & Problem Solving
USING TOOLS
Use a net to find the area of the entire surface of the solid. Explain your reasoning. (See Exploration 2, p. 311.)
Question 15.
Answer:
The surface area of the rectangle = length x breadth
area = l x b
Explanation:
The above figure is same as the rectangle
The surface area of the rectangle = length x breadth
area = l x b
Question 16.
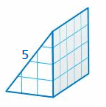
Answer:
The surface area of the triangle = (/2) x length x breadth
area =(1/2) x l x b
Explanation:
The above figure is the same as the triangle
The surface area of the rectangle =(1/2) x length x breadth
area =(1/2) l x b
Question 17.

Answer:
The surface area of the square = (/2) x length x breadth
area =(1/2) x l x b
Explanation:
The above figure is the same as the triangle
The surface area of the rectangle =(1/2) x length x breadth
area =(1/2) l x b
FINDING SURFACE AREA
Find the surface area of the rectangular prism.
Question 18.
Answer:
130 ft
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 5 x 1 + 5 x 1 + 10 x 5 + 10 x 5 + 10 x 1 +10 x 1
surface area = 5 + 5 + 50 + 50 +10 +10
surface area = 130
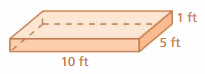
Question 19.
Answer:
198
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 6 x 9 + 6 x 9 + 9 x 3 + 9 x 3 + 6 x 3 +6 x 3
surface area = 54 + 54 + 27 + 27 +18 +18
surface area = 198 sq. cm
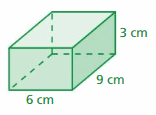
Question 20.
Answer:
76
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 2 x 4+ 2 x 4 + 4 x 5 + 4 x 5 + 2 x 5 +2 x 5
surface area = 8 + 8 + 20 + 20+10+10
surface area = 76
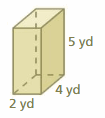
Question 21.
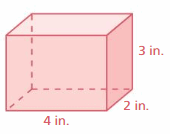
Answer:
52in
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 2 x 4+ 2 x 4 + 3 x 2 + 3 x 2 + 4 x 3 +4 x 3
surface area = 8 + 8 + 6 + 6 +12 +12
surface area = 52
Question 22.
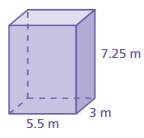
Answer:
116.375 m
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 5.5 x 3 + 5.5 x 3 + 3 x 7.25 + 3 x 7.25 + 5.5 x 7.25 + 5.5 x 7.25
surface area = 16.5+ 16.5 + 21.75 + 21.75 +39.875 +39.875
surface area = 116.375 m
Question 23.
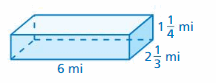
Answer:
48.785 mi
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 6 x2 .33 + 6 x 2.33 + 2.33 x 1.25 + 2.33 x 1.25 + 6 x 1.25 + 6 x 1.25
surface area = 13.98+ 13.98 + 2.9125 + 2.9125 +7.5 +7.5
surface area = 48.785 mi
FINDING SURFACE AREA
Find the surface area of the triangular prism.
Question 24.
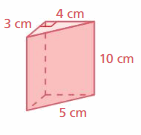
Answer:
102 cm
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 3 x 4 = 12 + (1/2) x 3 x 10 = 15 + (1/2) x 3 x 10 = 15 + 4 x 5 = 20 + 4 x 10 = 40
bottom = 3 x 4 , front = (1/2) x 3 x 10, back = (1/2) x 3 x 10, side = 4 x 5 , side = 4 x 10
surface area = 12 +15 +15+20 +40
area = 102 cm
Question 25.
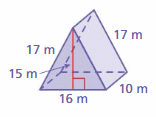
Answer:
822 m
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 16 x 10 = 160+ (1/2) x 16 x 17 = 136 + (1/2) x 16 x 17 = 136+ 15 x 10=150 + 15 x 16 = 240
bottom = 16 x 10 , front = (1/2) x16 x 17, back = (1/2) x 16 x 17, side = 15 x 10 , side =15 x 16
surface = 160 +136+ 136 + 150 + 240
area = 822 m
Question 26.
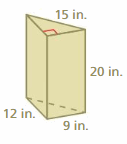
Answer:
543 in
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 12 x 9 = 108+ (1/2) x 12 x 10 = 60 + (1/2) x 12 x 10 = 60 + 15 x 9 = 135 + 9 x 20 = 180
bottom = 12 x 9 , front = (1/2) x12 x 10, back = (1/2) x 12 x 10, side = 115 x 9 , side = 9 x 20
surface area =108 +60 +60+ 135 +180
area = 543 in
Question 27.
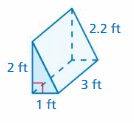
Answer:
17.8 ft
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 1 x 3 = 3+ (1/2) x 1 x 2.2 = 1.1 + (1/2) x 1 x 2.2 = 1.1 + 2 x 3 = 6+ 3 x 2.2 = 6.6
bottom = 1 x 3 , front = (1/2) x1 x 2.2, back = (1/2) x 1 x 2.2, side = 2 x 3 , side = 3 x 2.2
surface area =3 + 1.1 + 1.1+ 6 + 6.6
area = 17. 8 ft
Question 28.
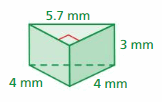
Answer:
62 . 8 mm
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 4 x 4 = 16+ (1/2) x 4 x 3 = 6 + (1/2) x 4 x 3 = 6 + 5.7 x 4=22.8+ 3 x 4 = 12
bottom = 4 x 4 , front = (1/2) x 4 x 3, back = (1/2) x 4 x 3, side = 5.7 x 4 , side = 3 x 4
surface area = 16 + 6 + 6 +22.8 + 12
area = 62. 8 mm
Question 29.
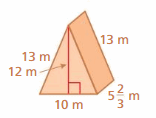
Answer:
3228 . 26 m
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 10 x (17/3) = 56.6+ (1/2) x 10 x 13 = 65 + (1/2) x 10 x 13 = 65 + 12 x (17/3) = 68+ (17/3) x 13 = 73.6
bottom = 10 x (17/3) , front = (1/2) x 10 x 13, back = (1/2) x 10 x 13, side = 12 x (17/3) , side = (17/3) x 13
surface area = 56.6 + 65 + 65 + 68 + 73.6
area = 3228. 26 m
Question 30.
MODELING REAL LIFE
A gift box in the shape of a rectangular prism measures 8 inches by 8 inches by 10 inches. What is the least amount of wrapping paper needed to wrap the gift box? Explain
Answer:
440 inches
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 8 x 8 + 8 x 8 + 10 x 8 + 10 x 8+ 8 x 10 + 8 x 10
surface area = 64 + 64+ 80 + 80 + 80 + 80
surface area = 440 in
The least amount of wrapping paper needed to wrap the gift box = 440 in
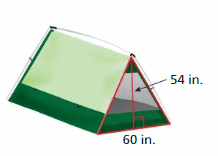
Question 31.
MODELING REAL LIFE
What is the least amount of fabric needed to make the tent?
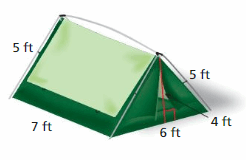
Answer:
102 sq. ft
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 6 x 4 = 24+ (1/2) x 6 x 5 = 15 + (1/2) x 6 x 5 = 15+ 7 x 4 = 28+ 5 x 4 = 20
bottom = 6 x 4 , front = (1/2) x 6 x 5, back = (1/2) x 6 x 5, side = 7 x 4 , side = 5 x 4
surface area = 24 + 15 + 15 + 28 + 20
area = 20 sq. ft
FINDING SURFACE AREA
Find the surface area of the cube.
Question 32.
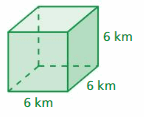
Answer:
216 sq. km
Explanation:
area of the cube = 6 s2
area = 6 x side x side
area = 6 x 6 x 6
area = 216 sq. km
Question 33.
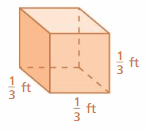
Answer:
0.66666 sq. ft
Explanation:
area of the cube = 6 s²
area = 6 x side x side
area = 6 x (1/2) x (1/2)
area = 6 x 0.11111
area = 0.6666 sq. ft
Question 34.
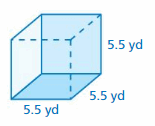
Answer:
181.5 sq. yd
Explanation:
area of the cube = 6 s²
area = 6 x side x side
area = 6 x 5.5 x 5.5
area = 6 x 30.25
area = 181 .5 sq. yd
Question 35.
MODELING REAL LIFE
A piece of dry ice is in the shape of a cube with edge lengths of 7 centimeters. Find the surface area of the dry ice.

Answer:
294 centimeters
Explanation:
area of the cube = 6 s2
area = 6 x side x side
area = 6 x 7 x 7
area = 6 x 49
area = 294 sq. cm
Question 36.
YOU BE THE TEACHER
Your friend finds the surface area of the prism. Is your friend correct? Explain your reasoning.

Answer:
No, my friend is not correct because my friend did the surface area of the cube
Explanation:
My friend did the surface area of the cube
cube = 6s²
Question 37.
CRITICAL THINKING
A public library has the aquarium shown. The front piece of glass has an area of 24 square feet. How many square feet of glass were used to build the aquarium?
Answer:
The square feet of glass were used to build the aquarium = 12 ft
Explanation:
The square feet of glass were used to build the aquarium = l x b
square = 6 x 2.5
square = 12
Question 38.
PROBLEM SOLVING
A cereal box has the dimensions shown.
a. Find the surface area of the cereal box.
b. The manufacturer decides to decrease the size of the box by reducing each of the dimensions by 1 inch. Find the decrease in surface area.

Answer:
a : 216 in
b : 144 in
Explanation:
Surface area of a = 6 x s x s
area = 6 x 36
area = 216
surface area of b = 6 x s x s
area = 6 x 24
area = 144 because they said that cereal box is decreased by 1 inch
Question 39.
REASONING
The material used to make a storage box costs $1.25 per square foot. The boxes have the same volume. Which box might a company prefer to make? Explain your reasoning.
Question 40.
LOGIC
Which of the following are nets of a cube? Select all that apply.
Question 41.
MODELING REAL LIFE
A quart of stain covers 100 square feet. How many quarts should you buy to stain the wheelchair ramp? (Assume you do not have to stain the bottom of the ramp.)
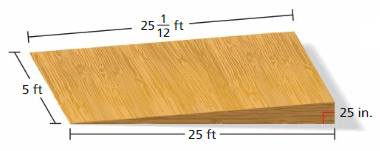
Answer:
Question 42.
DIG DEEPER!
A cube is removed from a rectangular prism. Find the surface area of the figure after removing the cube.
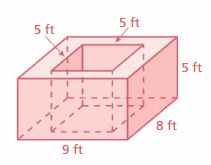
Answer:
341 sq. ft
Explanation:
Surface area of the rectangular prism = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 9 x 8= 72 + (1/2) x 9 x 5=94.5 + (1/2) x 9 x 5 = 94.5 + 5 x 8 = 40+ 8 x 5 =40
bottom = 9 x 8 , front = (1/2) x 9 x 5, back = (1/2) x 9 x 5, side = 5 x 8 , side = 8 x 5
surface area = 72 + 94.5 + 94.5 +40 +40
area = 341 sq. ft
Lesson 7.6 Surface Areas of Pyramids
EXPLORATION 1
Using a Net to Construct a Solid
Work with a partner. Copy the net shown below onto grid paper.
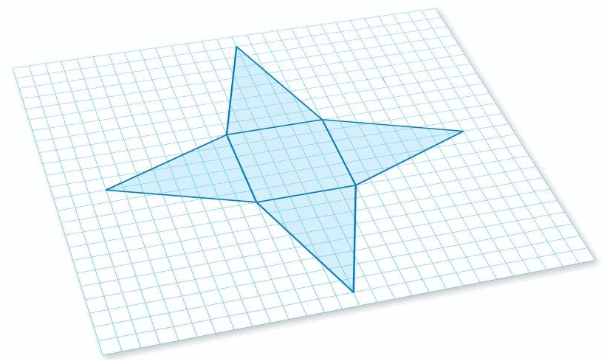
a. Cut out and fold the net to form a solid. What type of solid does the net form?
b. What is the surface area of the solid?
EXPLORATION 2
Finding Surface Areas of Solids
Work with a partner. Find the surface area of each solid. Explain your reasoning.

7.6 Lesson
Key Idea
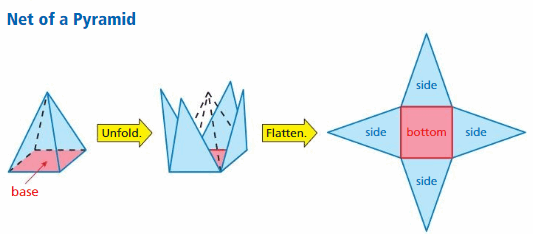
In this book, the base of every pyramid is either a square or an equilateral triangle. So, the lateral faces are identical triangles.
Try It
Find the surface area of the square pyramid.
Question 1.
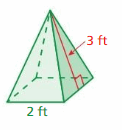
Answer:
16 sq. ft
Explanation:
surface area of the square pyramid = bottom + side + side + side + side
area = 4 + 3 + 3 + 3
bottom = 2 x 2= 4, side = (1/2) x 2 x 3 = 3,
area = 16 sq. ft
Question 2.
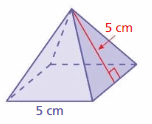
Answer:
62.5 sq. cm
Explanation:
surface area of the square pyramid = bottom + side + side + side + side
area = 25 + 12.5 + 12.5 + 12.5
bottom = 5 x 5 = 25, side = (1/2) x 5 x 5 = 12.5,
area = 62.5 sq. cm
Try It
Find the surface area of the triangular pyramid.
Question 3.
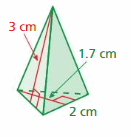
Answer:
area = 26 sq. cm
Explanation:
surface area of the triangular pyramid = bottom + side + side + side
area = 17 + 3 + 3 + 3
bottom = (1/2 ) x 3 x 4 = 17 , side =(1/2) x 3 x 2 = 3
area = 26 sq. cm
Question 4.
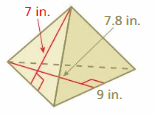
Answer:
area = 26 sq. cm
Explanation:
surface area of the triangular pyramid = bottom + side + side + side
area = 17 + 3 + 3 + 3
bottom = (1/2 ) x 3 x 4 = 17 , side =(1/2) x 3 x 2 = 3
area = 26 sq. cm
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
PRECISION
Explain how to find the surface area of a pyramid.
Answer:
Surface area of the pyramid = area +(1/2) x p x s
Explanation:,
The surface area of the pyramid = area + (1/2) x p x s where p = perimeter of the base, s = slant height
FINDING SURFACE AREA
Find the surface area of the pyramid.
Question 6.
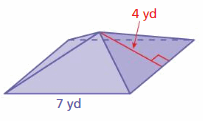
Answer:
Area = 21 sq. yd
Explanation:,
The surface area of the pyramid = area + (1/2) x p x s where p = perimeter of the base, s = slant height
area = 7 +(1/2) x 4 x 7
area = 7 + 14
area = 21 sq. yd
Question 7.
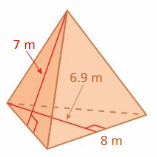
Answer:
Area = 31.15 sq. m
Explanation:,
The surface area of the pyramid = area + (1/2) x p x s where p = perimeter of the base, s = slant height
area = 8 +(1/2) x 7 x 6.9
area = 7 + (48.3/2)
area = 7 + 24.15
area = 31.15 sq. m
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 8.
A salt lamp is shaped like a triangular pyramid. Find the surface area of each triangular face.
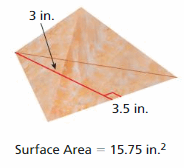
Answer:
The surface area of the triangular pyramid = 115.5 sq. in
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 3 in
area of the face2 = 3 in
area of the face3 = 3 in
area of the face4 = 3in
area of the base = 3.5
surface area = 12 + 3.5 = 15.5 sq. in
Question 9.
DIG DEEPER!
Originally, each triangular face of the Great Pyramid of Giza had a height of 612 feet and a base of 756 feet. Today, the height of each triangular face of the square pyramid is 592 feet. Find the change in the total surface area of the four triangular faces of the Great Pyramid of Giza.

Answer:
The surface area of the four triangular faces = 612 sq. ft
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 612 sq. ft
area of the face2 = 612 sq. ftft
area of the face3 =612 sq. ft
area of the face4 = 612 sq. ft
area of the base = 756 sq. ft
surface area = 3204 sq. ft
Surface Areas of Pyramids Homework & Practice 7.6
Review & Refresh
Find the surface area of the prism.
Question 1.
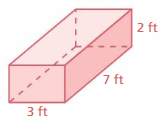
Answer:
82 sq. ft
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 7 x 2 + 7 x 2 + 7 x 3+ 7 x 3 + 3 x 2 + 3 x 2
surface area = 14 +14+ 21 + 21 +6+6
surface area = 82 sq. ft
Question 2.
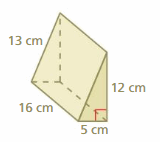
Answer:
82 sq. ft
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = + 7 x 2 + 7 x 3+ 7 x 3 + 3 x 2 + 3 x 2
surface area = 14 +14+ 21 + 21 +6+6
surface area = 82 sq. ft
Question 3.
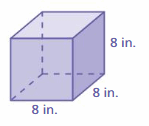
Answer:
384 sq. in
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area =8 x 8 + 8 x 8 + 8 x 8+ 8 x 8 + 8 x 8 + 8 x 8
surface area = 64 +64 + 64 + 64+ 64+64
surface area = 384 sq. in
Match the expression with an equivalent expression.
Question 4.
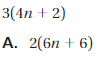
Answer:
12n + 6
A. 12n + 12
Explanation:
3 x (4n + 2 )
12n + 6
A. 2 x (6n + 6)
12n + 12
Question 5.
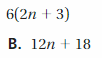
Answer:
12n + 18
B. 6(2n + 3)
Explanation:
6 x (2n + 3 )
12n + 18
A. 6 x (2n + 3)
12n + 18
Question 6.
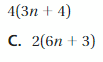
Answer:
12n + 16
C. 12n + 6
Explanation:
4 x (3n + 4 )
12n + 16
C. 2 x (6n + 3)
12n + 6
Question 7.
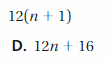
Answer:
12n + 12
D. 2 x (6n +8)
Explanation:
4 x (3n + 3)
12n + 12
C. 2 x (6n + 8)
12n + 16
Write the fraction or mixed number as a percent.
Question 8.
\(\frac{17}{25}\)
Answer:
68%
Explanation:
(17/25) = (17/25 x 100)
(17 x 4)/(25 x 4)
(68/100)
(34/50)
68%
Question 9.
\(\frac{19}{20}\)
Answer:
95%
Explanation:
(19/20) = (19/20 x 100)
(19 x 5)/(20 x 5)
(95/100)
95%
Question 10.
6\(\frac{7}{8}\)
Answer:
6.875%
Explanation:
(7/8) = (7/8 x 100)
6 x (7/8) = 6 x (7/8 x 100)
(55/8)
Question 11.
\(\frac{3}{400}\)
Answer:
0.75%
Explanation:
(3/400) = (3/400 x 100)
(3/4) = 0.75%
Concepts, Skills, &Problem Solving
USING TOOLS
Use a net to find the surface area of the solid. Explain your reasoning. (See Exploration 2, p. 319.)
Question 12.
Answer:
The surface area of the triangular pyramid = a+(1/2) x p x s
Explanation:
The surface area of the pyramid = area + (1/2) x p x s where p = perimeter of the base, s = slant height
Question 13.
Answer:
The surface area of the triangular pyramid = a+(1/2) x p x s
Explanation:
The surface area of the pyramid = area + (1/2) x p x s where p = perimeter of the base, s = slant height
Question 14.
Answer:
The surface area of the triangular pyramid = a+(1/2) x p x s
Explanation:
The surface area of the pyramid = area + (1/2) x p x s where p = perimeter of the base, s = slant height
FINDING SURFACE AREA
Find the surface area of the pyramid.
Question 15.
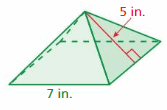
Answer:
The surface area of the pyramid = 27 in
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 5 sq. in
area of the face2 = 5 sq. in
area of the face3 = 5 sq. in
area of the face4 = 5 sq. in
area of the base = 7 sq. in
surface area = 27 sq. in
Question 16.
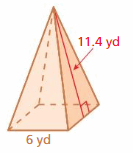
Answer:
The surface area of the pyramid = 51 .6 sq. yd
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 11.4 sq. yd
area of the face2 = 11.4 sq. yd
area of the face3 = 11.4 sq. yd
area of the face4 = 11.4 sq. yd
area of the base = 6 sq. yd
surface area = 51.6 sq. yd
Question 17.
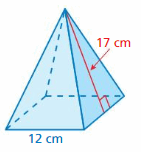
Answer:
The surface area of the pyramid = 80 sq. cm
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 17 sq. cm
area of the face2 = 17 sq. cm
area of the face3 = 17 sq. cm
area of the face4 = 17 sq. cm
area of the base = 12 sq. cm
surface area = 80 sq. cm
Question 18.
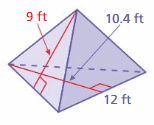
Answer:
The surface area of the pyramid = 50.8 sq. ft
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 10.4 sq. ft
area of the face2 = 10.4 sq. ft
area of the face3 = 9 sq. ft
area of the face4 = 9 sq. ft
area of the base = 12 sq. ft
surface area = 50.8 sq. ft
Question 19.
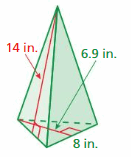
Answer:
The surface area of the pyramid = 49.8 sq. in
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 6.9 sq. in
area of the face2 = 6.9 sq. in
area of the face3 = 14 sq. in
area of the face4 = 14 sq. in
area of the base = 8 sq. in
surface area = 49.8 sq. in
Question 20.
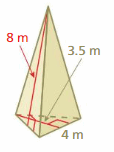
Answer:
The surface area of the pyramid = 27 sq. m
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 8 sq. m
area of the face2 = 8 sq. m
area of the face3 = 3.5 sq. m
area of the face4 = 3.5 sq. m
area of the base = 4 sq. m
surface area = 27 sq. m
Question 21.
MODELING REAL LIFE
A paperweight is shaped like a triangular pyramid. Find the surface area of the paperweight.
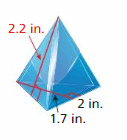
Answer:
The surface area of the pyramid = 9.8 sq. in
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 2.2 sq. in
area of the face2 = 2.2 sq. in
area of the face3 = 1.7 sq. in
area of the face4 = 1.7 sq. in
area of the base = 2 sq. in
surface area = 9.8 sq. in
Question 22.
PROBLEM SOLVING
The entrance to the Louvre Museum in Paris, France, is a square pyramid. The side length of the base is 116 feet, and the height of one of the triangular faces is 91.7 feet. Find the surface area of the four triangular faces of the entrance to the LouvreMuseum.

Answer:
The surface area of the pyramid = 48.2 sq. ft
Explanation:
The surface area of the triangular pyramid = area of the faces + area of the base
area of the face1 = 91.7 sq. ft
area of the face2 = 91.7 sq. ft
area of the face3 = 91.7 sq. ft
area of the face4 = 91.7 sq. ft
area of the base = 116 sq. ft
surface area = 482.8 sq. ft
Question 23.
MODELING REAL LIFE
A silicon wafer is textured to minimize light reflection. This results in a surface made up of square pyramids. Each triangular face of one of the pyramids has a base of 5 micrometers and a height of 5.6 micrometers.Find the surface area of the pyramid, including the base.
Answer:
Area = 42 sq. micrometers
Explanation:,
The surface area of the pyramid = area + (1/2) x p x s where p = perimeter of the base, s = slant height
area = 28 +(1/2) x 5 x 5.6
area = 28+ (28/2)
area = 28+ 14
area = 42 sq. micrometers
Question 24.
REASONING
A hanging light cover made of glass is shaped like a square pyramid. The cover does not have a bottom. One square foot of the glass weighs 2.45 pounds. The chain can support 35 pounds. Will the chain support the light cover? Explain.
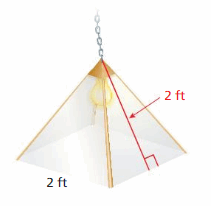
Answer:
Yes the chain support the light cover
Explanation:
The surface area of the pyramid = area + (1/2) x p x s where p = perimeter of the base, s = slant height
area = 4+(1/2) x 2 x 2
area = 4+ 4
area = 8
area = 8 sq. ft
Question 25.
GEOMETRY
The surface area of the square pyramid shown is 84 square inches. What is the value of x?
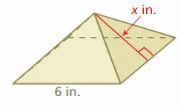
Answer:
The value of x = 14 in
Explanation:
The surface area of the square pyramid = length x breadth
area = l x b
84 =6x
x =(84/6)
x =14 in
Question 26.
STRUCTURE
In the diagram of the base of the hexagonal pyramid, all the triangles are the same. Find the surface area of the hexagonal pyramid.
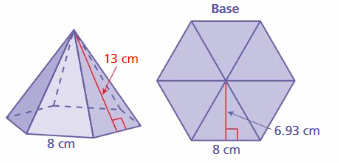
Answer:
The surface area of the hexagonal pyramid = 478.32 cm
Explanation:
The surface area of the hexagonal pyramid = 3ab +3bs
area = 3 x 8 x 6.93 +3 x 8 x 13 where a = 8,b =8, s = 13
area = 166.32+312
area = 478.32 sq. cm
Question 27.
CRITICAL THINKING
Can you form a square pyramid using a square with side lengths of 14 inches and four of the triangles shown? Explain your reasoning.
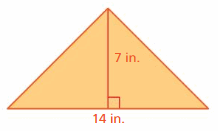
Answer:
yes
Explanation:
given that square has side lengths of 14 inches and four of the triangles.
so we can form the square pyramid
Lesson 7.7 Volumes of Rectangular Prisms
Recall that the volume of a three-dimensional figureis a measure of the amount of space that it occupies. Volume is measured in cubic units.
EXPLORATION 1
Using a Unit Cube
Work with a partner. A unit cube is a cube with an edge length of 1 unit. The parallel edges of the unit cube have been divided into 2, 3, and 4 equal parts to create smaller rectangular prisms that are identical.
a. The volumes of the identical prisms are equal. What else can you determine about the volumes of the prisms? Explain.
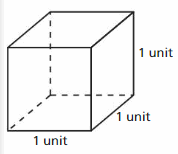
Answer:
The volume of the prism = 1 unit
Explanation:
The volume of the prism = Bh
where b = area of the base
volume = 1 x 1
volume = 1
b. Use the identical prisms in part(a) to find the volume of the prism below. Explain your reasoning.
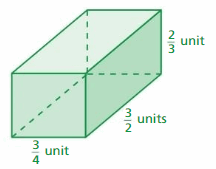
Answer:
The volume of the prism = 4.3125 cu. unit
Explanation:
The volume of the prism = Bh
where b = area of the base
volume = (3/4) x (2/3)
volume = 0.75 x 5.75
volume = 4.3125 cu. units
c. How can you use a unit cube to find the volume of the prism below? Explain.
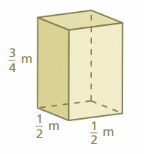
Answer:
The volume of the prism = 0.375 cu. m
Explanation:
The volume of the prism = Bh
where b = area of the base
volume = (1/2) x (3/4)
volume = 0.5x 0.75
volume = 0.375 cu. m

d. Do the formulas V = Bh and V = ℓwh work for rectangular prisms with fractional edge lengths? Give examples to support your answer.
7.7 Lesson
Key Idea
Volume of a Rectangular Prism
Words
The volume V of a rectangular prism is the product of the area of the base and the height of the prism.
Algebra
V = Bh or V = lwh
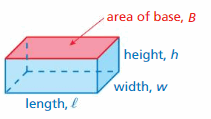
When a rectangular prism is a cube with an edge length of s, you can also use the formula V = s3 to find the volume V of the cube.

Try It
Find the volume of the prism.
Question 1.
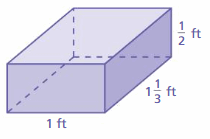
Answer:
The volume of the prism = 0.6665 cu. ft
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (1.333) x (0.5)
volume = 1.33 x 0.5
volume = 0.6665 cu. ft
Question 2.
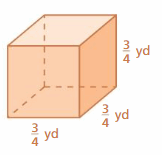
Answer:
The volume of the prism = 0.6665 cu. ft
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (1.333) x (0.5)
volume = 1.33 x 0.5
volume = 0.6665 cu. ft
Try It
Find the missing dimension of the prism.
Question 3.

Answer:
The missing dimension of the prism = 6 in
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = b x l x h
volume = 6x 6 x 2
volume = 72 in
so length = 6 in
Question 4.
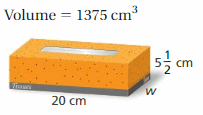
Answer:
The width of the prism = 12.5 cm
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = 5 x(1/2) x 12.5 x20
volume = (11/2)x 12.5 x 20
volume = 1375 cm
so width = 12.5 cm
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 5.
CRITICAL THINKING
Explain how volume and surface area are different.
Answer:
Volume grows exponentially and the surface area grows with the volume
the surface area grows with the rate of volume
Question 6.
FINDING A MISSING DIMENSION
The base of a rectangular prism has an area of 24 square millimeters. The volume of the prism is 144 cubic millimeters. Make a sketch of the prism. Then find the height of the prism.
Answer:
The height of the prism = 6 millimeters
Explanation:
The volume of the rectangular prism = Bh
where b = base area and h= height
so volume = 144 cubic millimeters given
B = 24
volume = Bh
144 = 24h
h = (144/24)
h = 6 mm
FINDING VOLUME
Find the volume of the prism.
Question 7.
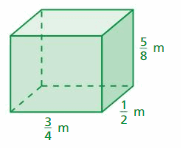
Answer:
The volume of the prism = 0.2343 cu. m
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (3/4) x(1/2) x (5/8)
volume = 0.75 x 0.5x 0.625
volume = 0.2343 cu. m
Question 8.
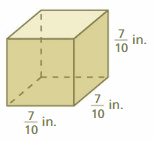
Answer:
The volume of the prism = 0.343 cu. in
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (7/10) x(7/10) x (7/10)
volume = 0.7 x 0.7 x 0.7
volume = 0.343 cu. in
When finding volumes, you may need to convert cubic units. The diagrams at the left show that there are 27 cubic feet per cubic yard.
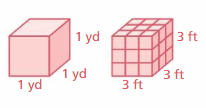
1 yd3 = (1 yd)(1 yd)(1 yd) = (3 ft)(3 ft)(3 ft) = 27 ft3
You can use a similar procedure to convert other cubic units.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 9.
DIG DEEPER!
The shark cage is in the shape of a rectangular prism and has a volume of 315 cubic feet. Find a set of reasonable dimensions for the base of the cage. Justify your answer.
Answer:
The base of the prism = 4.906 ft
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
314 = (8) x(8 ) x h
314 = 64h
h = (314/64)
h = 4.906 ft
Question 10.
The hot tub is in the shape of a rectangular prism. How many pounds of water can the hot tub hold? One cubic foot of water weighs about 62.4 pounds.

Answer:
The hot tub can hold = 312 pounds
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
hot tub = (2) x(2) x 1.25
hot tub = 4 x 1.25
hottub = 5
hot tub = 5
5 x 62.4 = 312 pounds
Volumes of Rectangular Prisms Homework & Practice 7.7
Review & Refresh
Find the surface area of the pyramid.
Question 1.
Answer:
The surface area of the pyramid = 220.5 sq. ft
Explanation:
The surface area of the pyramid = area + (1/2) x p x s
where area = l x w
surface area =21 x (1/2) x 7 x3
surface area = 21x 10.5
surface area = 220.5 sq. ft
Question 2.
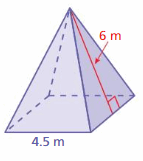
Answer:
The surface area of the pyramid = 364.5 sq. m
Explanation:
The surface area of the pyramid = area + (1/2) x p x s
where area = l x w
surface area =27 x (1/2) x 4.5 x6
surface area = 27 x (27/2)=13.5
surface area = 364.5 sq. m
Question 3.
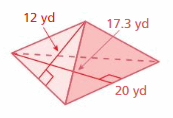
Answer:
The surface area of the pyramid = 20,760 sq. yd
Explanation:
The surface area of the pyramid = area + (1/2) x p x s
where area = l x w
surface area =346 x (1/2) x 12 x 20
surface area = 346 x (120/2)=60
surface area = 20,760 sq. yd
Write the phrase as an expression. Then evaluate the expression when x = 2 and y = 12.
Question 4.
8 more than a number x
Answer:
Yes
Explanation:
8 is more than 2
where x = 2 given
Question 5.
the difference of a number y and 9
Answer:
The difference of a number y and 9 = 3
Explanation:
difference = 12 – 9
diff = 3
where y = 12 given
Concepts, Skills, & Problem Solving
STRUCTURE
The unit cube is divided into identical rectangular prisms. What is the volume of one of the identical prisms? (See Exploration 1, p. 325.)
Question 6.
Answer:
(2/2),(2/4),(4/2)
Explanation:
In the above figure the base = (2/2) units
base = (2/2) units
height = (4/2) units
Question 7.
Answer:
(3/3),(3/2),(2/3)
Explanation:
In the above figure the base = (3/3) units
base = (3/2) units
height = (2/3) units
Question 8.
Answer:
(5/5),(5/3),(3/5)
Explanation:
In the above figure the base = (5/5) units
base = (5/3) units
height = (3/5) units
FINDING VOLUME
Find the volume of the prism.
Question 9.
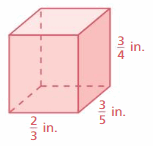
Answer:
The volume of the prism = 0.297 Cu. in
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (0.66) x(0.6) x (0.75)
volume = 0.297 Cu. in
Question 10.
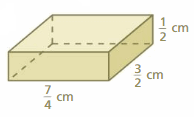
Answer:
The volume of the prism = 1.3125 Cu. cm
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (7/4) x(3/2) x (1/2)
volume = 1.75 x 1.5 x 0.5
volume = 1.3125 Cu. cm
Question 11.
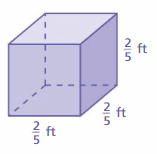
Answer:
The volume of the prism = 0.064 Cu. ft
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (2/5) x(2/5) x (2/5)
volume = 0.4 x 0.4 x 0.4
volume = 0.064 Cu. ft
Question 12.
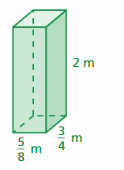
Answer:
The volume of the prism =0.75 Cu. m
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (5/8) x(3/4) x (2)
volume = 0.625 x 0.6 x 2
volume = 0.75 Cu. m
Question 13.
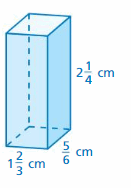
Answer:
The volume of the prism =3.111255 Cu. cm
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (5/3) x(5/6) x (9/4)
volume = 1.66 x 0.833 x 2.25
volume = 3.111255 Cu. cm
Question 14.
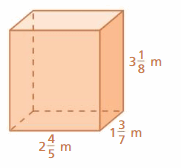
Answer:
The volume of the prism = 12.425 Cu. m
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (14/5) x(10/7) x (25/8)
volume = 2.8 x 1.42 x 3.125
volume = 12.425 Cu. m
FINDING A MISSING DIMENSION
Find the missing dimension of the prism.
Question 15.
Volume = 1620 cm3
Answer:
The missing dimension of the prism = 20 cm
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
1620 = (9) x(9) x h
1620 = 81 h
h = (1620/8)
h = 8
Question 16.
Volume = 220.5 cm3
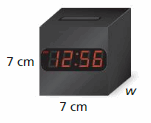
Answer:
The missing dimension of the prism = 4.5 cm
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
220.5 = (7) x(7) x w
220.5 = 49 w
w = (220.5/49)
w = 4.5 cm
Question 17.
Volume = 532 in3

Answer:
The missing dimension of the prism = 16 in
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
532 = (7/4) x(19) x w
532 = 33.25
h = (532/33.25)
h = 16 in
Question 18.
MODELING REAL LIFE
An FBI agent orders a block of ballistics gel. The gel weighs 54 pounds per cubic foot. What is the weight of the block of gel?
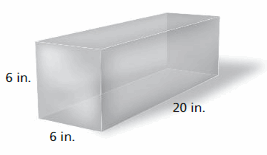
Answer:
The volume of the prism = 720 in
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (6) x(20) x 6
volume = 720 in
Question 19.
MODELING REAL LIFE
a. Estimate the amount of casserole left in the dish.
b. Will the casserole fit in the storage container? Explain your reasoning.

Answer:
a : The amount of casserole left in the dish = 396 in
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (2.75) x(12) x 12
volume = 396
b : The casserole will not fit in the container
Explanation:
The length of the container is less than the casserole
Question 20.
GEOMETRY
How many \(\frac{3}{4}\)-centimeter cubes do you need to create a cube with an edge length of 12 centimeters?
Answer:
16 cubes
Explanation:
16 cubes are used to create a cube with an edge length of 12 centimeters
in the above-given question (3/4) = 0.75
0.75 x 16 = 12
Question 21.
REASONING
How many one-millimeter cubes do you need to fill a cube that has an edge length of 1 centimeter? How can this result help you convert a volume from cubic millimeters to cubic centimeters? from cubic centimeters to cubic millimeters?
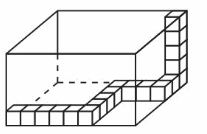
Answer:
10 mm cubes are needed to fill a cube that has an edge length of 1 cm
Explanation:
1 mm =0.1 cm
0.1 x 10 = 1 cm
1 cubic mm = 0.001 cubic cm
1 cubic cm = 1000 cubic mm
Question 22.
LOGIC
The container is partially filled with unit cubes. How many unit cubes fit in the container? Explain your reasoning.
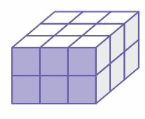
Answer:
6 cubes fit in the container
Explanation:
In the above diagram,6 units are filled with color
so 6 unit cubes fit in the container.
Question 23.
PROBLEM SOLVING
The area of the shaded face is 96 square centimeters. What is the volume of the rectangular prism?
Answer:
The volume of the rectangular prism = 4 x 3 x 8
Explanation:
The volume of the rectangular prism = length x width x height
volume = 4 x 3 x 8
Question 24.
DIG DEEPER!
Is the combined volume of a 4-foot cube and a 6-foot cube equal to the volume of a 10-foot cube? Use a diagram to justify your answer.
Question 25.
PROJECT
You have 1400 square feet of boards to use for a new tree house.
a. Design a tree house that has a volume of at least 250 cubic feet. Include sketches of your tree house.
b. Are your dimensions reasonable? Explain your reasoning.
Area, Surface Area, and Volume Connecting Concepts
Using the Problem-Solving Plan
Question 1.
A sports complex has two swimming pools that are shaped like rectangular prisms. The amount of water in the smaller pool is what percent of the amount of water in the larger pool?
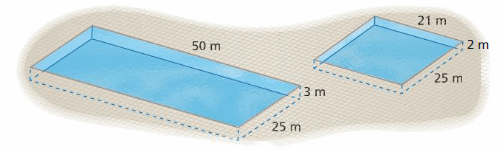
Understand the problem.
You know the shape and the dimensions of the two swimming pools. You are asked to find the amount of water in the smaller pool as a percent of the amount of water in the larger pool.
Make a plan.
First, find the volume of each pool. Then represent the amount of water in the smaller pool as a fraction of the amount of water in the larger pool. Find an equivalent fraction whose denominator is 100 to find the percent.
Answer:
28% of water in the 1st pool is greater than that of the smaller pool
Explanation:
volume of the first pool = 25 x 3 x 50=3750
volume of the second pool = 25 x 21 x 2= 1050
1050 : 3750 = 0.28
0.28 = 28 %
Solve and Check
Use the plan to solve the problem. Then check your solution.
Question 2.
Use a graph to represent the relationship between the surface area S(in square meters) and the height h(in meters) of the triangular prism. Then find the height when the surface area is 260 square meters.
Answer:
The height of the triangular prism = 43.33 meters
Explanation:
The surface area of the triangular prism = (1/2) x b x h
area = (1/2) x 12h
260 = 6h
h =(260/6)
h = 43.33 m
Question 3.
A toy company sells two different toy chests. The toy chests have different dimensions, but the same volume. What is the width w of Toy Chest 2?

Answer:
The width of the toy chest2 = 384 in
Explanation:
In the above figure the toy chest 2 has length = 24 in and volume = 16 in
width = 24 x 16
width = 384 in
Performance Task
Maximizing the Volumes of Boxes
At the beginning of this chapter, you watched a STEAM Video called “Packaging Design.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.
Area, Surface Area, and Volume Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Answer:
polygon = a polygon is a closed figure in a plane that is made up of 3 or more line segments that intersect only at their endpoints.
composite figure = composite figure is made up of triangles, squares, rectangles and other two-dimensional figures.
kite = kite is a quadrilateral that has two pairs of adjacent sides with the same length and opposite sides with different lengths.
Graphic Organizers
You can use a Four Square to organize information about a concept. Each of the four squares can be a category, such as definition, vocabulary, example, non-example, words, algebra, table, numbers, visual, graph, or equation. Here is an example of a Four Square for the area of a parallelogram.
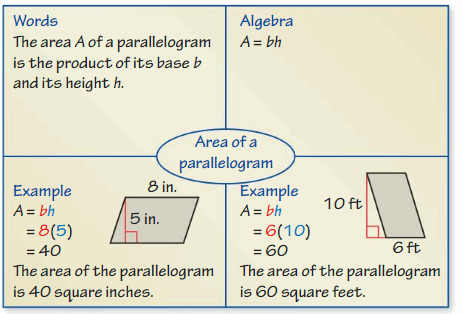
Choose and complete a graphic organizer to help you study the concept.
- area of a triangle
- area of a trapezoid
- area of a composite figure
- polyhedron
- surface area of a prism
- surface area of a pyramid
- volume of a rectangular prism

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

7.1 Areas of Parallelograms (pp. 285–290)
Find the area of the parallelogram.
Question 1.
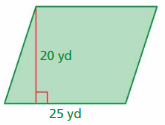
Answer:
area = 500 yd
Explanation:
area of the parallelogram = b x h
area = 25 x 20
area = 500 yd
Question 2.
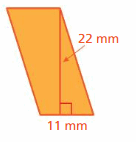
Answer:
area = 242 mm
Explanation:
area of the parallelogram = b x h
area = 22 x 11
area = 242 mm
Question 3.
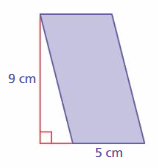
Answer:
area = 45 cm
Explanation:
area of the parallelogram = b x h
area = 9 x 5
area = 45 cm
Question 4.
Find the area (in square inches) of the parallelogram.
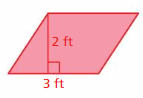
Answer:
area = 72 square in
Explanation:
area of the parallelogram = b x h
area = 2 x 3
area = 6 ft
1 feet = 12 inches
area = 72 square inches
Question 5.
The billboard shown is in the shape of a parallelogram with a base of 48 feet. What is the height of the billboard?

Answer:
The height of the billboard = 14 ft
Explanation:
The area of the parallelogram = b x h
672 = 48 h
h = (672/48)
h = 14 ft
Question 6.
The freeway noise barrier shown is made of identical parallelogram-shaped sections. The area of each section is 7.5 square meters, and the height of the barrier is 5 meters. How many meters wide is each section of the noise barrier?

Answer:
Each section of the noise barrier is 1.5 m
Explanation:
The area of the parallelogram = b x h
area = 1.5 x5
area = 7.5
so b = 1.5 m
Question 7.
Draw a parallelogram that has an area between 58 and 60 square centimeters.
Answer:
59 square centimeters
Explanation:
7.2 Areas of Triangles (pp. 291–296)
Find the area of the triangle.
Question 8.
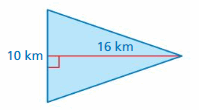
Answer:
The area of the triangle = 80 sq. km
Explanation:
The area of the triangle = half the product of the base and the product of the height
area = (1/2) x 16 x 10
area = (1/2) x 160
area = 80 sq. km
Question 9.
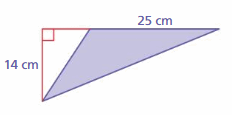
Answer:
The area of the triangle = 175 sq. cm
Explanation:
The area of the triangle = half the product of the base and the product of the height
area = (1/2) x 14 x 25
area = (1/2) x 350
area = 175 sq. cm
Find the missing dimension of the triangle.
Question 10.
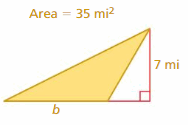
Answer:
base = 5 mi
Explanation:
The area of the tringle = b x h
given that h = 7 mi and area = 35 mi
base = 5 mi
Question 11.
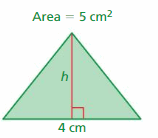
Answer:
height = 5 cm
Explanation:
The area of the tringle = b x h
given that b = 4 cm and area = 5 mi
height = 5 cm
Find the area of the figure.
Question 12.
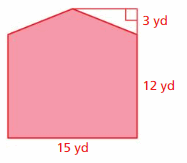
Answer:
The area of the trapezoid = 112.5 sq. yd
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (12 + 3). Given that b1 = 12 and b2 = 3
area = (1/2) x 15(15) given that h = 15 yd
area = (1/2) x 225
area = 112.5 sq. yd
Question 13.
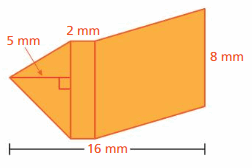
Answer:
The area of the trapezoid = 4 sq. mm
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (8 + 8). Given that b1 = 8 and b2 = 8
area = (1/2) x 2(16) given that h = 2 yd
area = (1/2) x 8
area = 4 sq. mm
Question 14.
Draw a composite figure that has an area of less than 35 square inches.
Answer:
The area of the triangle = b x h
area = 6 x 4
area = 24 square inches
Explanation:

Question 15.
Te triangle-shaped entrance to the cavern is 2\([\frac{1}{2}/latex] feet tall and 4 feet wide. What is the area of the entrance?

Answer:
The area of the entrance = 10
Explanation:
2 x(1/2) = 5/2 = 2.5
2.5 x 4 = 10
7.3 Areas of Trapezoids and Kites (pp. 297 – 304)
Question 16.
Use decomposition to find the area of the kite.
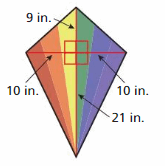
Answer:
The area of the kite = 255 sq. in
Explanation:
The area of the trapezoid = (1/2) x 10 x 9 + 10 x 21
area = (1/2) x 90 +210
area = 45 + 210
255 sq. in
Find the area of the trapezoid.
Question 17.
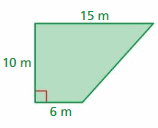
Answer:
The area of the trapezoid = 105 sq. m
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (15 + 6). Given that b1 = 15 and b2 = 6
area = (1/2) x 10(21) given that h = 10 in
area = (1/2) x 210
area = 105 sq. m
Question 18.
Answer:
The area of the trapezoid = 6 sq. in
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (1.5 + 2.5). Given that b1 = 1(1/2) = 1.5 and b2 = 2(1/2) = 2.5
area = (1/2) x 3(4) given that h = 10 in
area = (1/2) x 12
area = 6 sq. in
Question 19.
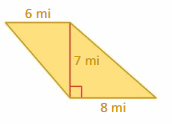
Answer:
The area of the trapezoid =49 sq. mi
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (6 + 8). Given that b1 = 6 and b2 = 8
area = (1/2) x 7(14) given that h = 7 mi
area = (1/2) x 98
area = 49 sq. mi
Find the area of the figure.
Question 20.
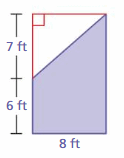
Answer:
The area of the trapezoid = 56 sq. ft
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (6 + 7). Given that b1 = 6 and b2 = 7
area = (1/2) x 8(14) given that h = 8 ft
area = (1/2) x 112
area = 56 sq ft
Question 21.
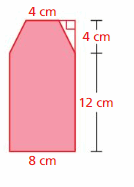
Answer:
The area of the trapezoid = 48 sq. cm
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (4 + 8). Given that b1 = 4 and b2 = 8
area = (1/2) x 8(12) given that h = 8 ft
area = (1/2) x 96
area = 48 sq. cm
Question 22.
Answer:
The area of the trapezoid = 40 sq. in
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (6 +10). Given that b1 = 6 and b2 = 10
area = (1/2) x 5(16) given that h = 80
area = (1/2) x 80
area = 40 sq. in
Question 23.
You are creating a design for the side of the soapbox car. How much area do you have for the design?
Answer:
The area of the trapezoid =240 sq. in
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (6 +14). Given that b1 = 6 and b2 = 14
area = (1/2) x 24(20) given that h = 24
area = (1/2) x 480
area = 240 sq. in
Question 24.
Find the area (in square centimeters) of a trapezoid with a height of 2 meters and base lengths of 3 meters and 5 meters.
Answer:
The area of the trapezoid =240 sq. in
Explanation:
The area of the trapezoid = one half the product of its height h and the sum of its bases b1 and b2.
area = (1/2) x h x( b1 + b2)
area =(1/2) x h (3 +5). Given that b1 = 3 and b2 = 5
area = (1/2) x 2(8) given that h = 2
area = (1/2) x 16
area = 8 sq. m
1 meter = 100 cm
area = 8 x 100 = 800 sq. cm
7.4 Three-Dimensional Figures (pp. 305–310)
Find the numbers of faces, edges, and vertices of the solid.
Question 25.
Answer:
faces = 6
edges = 12
vertices =7
Explanation:
The number of faces = 6
The number of edges = 12
The number of vertices =7
Question 26.
Answer:
faces = 5
edges = 10
vertices =6
Explanation:
The number of faces = 5
The number of edges = 10
The number of vertices =6
Question 27.
Answer:
faces = 9
edges = 20
vertices = 12
Explanation:
The number of faces = 9
The number of edges = 20
The number of vertices =12
Draw the solid.
Question 28.
square pyramid
Answer:
Question 29.
hexagonal prism
Draw the front, side, and top views of the solid.
Question 30.
Answer:
front = 1
side =2
top = 1
Explanation:

Question 31.

Answer:
front = 4
side =2
top = 2
Explanation:

Question 32.
Answer:
front = 1
side = 1
top = 1
7.5 Surface Areas of Prisms (pp. 311–318)
Find the surface area of the prism.
Question 33.
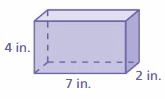
Answer:
The surface area of the prism = 100 sq. in
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 7 x 2 + 7 x 2 + 4x 7+ 4 x 7 + 4 x 2 + 4 x 2
surface area = 14 +14+ 28 + 28 +8+8
surface area = 100 sq. in
Question 34.
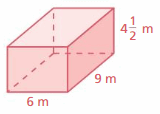
Answer:
The surface area of the prism = 243 sq. m
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 6 x 9 + 6 x 9 + 9 x 4.5+ 9 x 4.5 + 6 x 4.5 + 6 x 4.5
surface area = 54 +54+ 40.5 + 40.5 +27+ 27
surface area = 243 sq. m
Question 35.
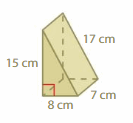
Answer:
The surface area of the prism = 590 cm
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 8 x 7 + 8 x 7 + 15 x 8+ 15 x 8 + 17 x 7 + 17 x 7
surface area = 56 +56+ 120 + 120 +119+ 119
surface area = 590 sq. cm
Question 36.
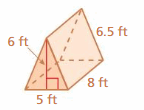
Answer:
The surface area of the triangular prism = 49 sq. ft
Explanation:
The surface area of the triangular prism = 2 b + p s
surface area = 2 x 5 +6 x 6.5
surface area = 10 + 39
surface area = 49 sq. ft
Question 37.
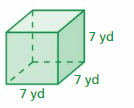
Answer:
The volume of the prism = 1,17,649 cu. yd
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (7) x(7) x (7)
volume = 49 x 49 x 49
volume = 1,17,649 cu. yd
Question 38.
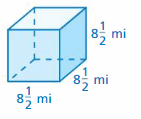
Answer:
The volume of the prism = 614.125 cu. mi
Explanation:
The volume of the prism = Bh
where b = l x w
where b = area of the base
volume = (17/2) x(17/2) x (17/2)
volume = 8.5 x 8.5 x 8.5
volume = 614.125 cu. mi
Question 39.
One quart of water-resistant paint covers 75 square feet. A swimming pool is in the shape of a rectangular prism with a length of 20 feet, a width of 10 feet, and a height of 5 feet. How many quarts should you buy to paint the swimming pool with two coats of paint?
Answer:
The volume of rectangular prism = 1000 cu. ft
Explanation:
The volume of the rectangular prism = b ase x height
volume = b x h where b = l x w
volume = 20 x 10 x 5
volume = 1000 cu. ft
7.6 Surface Areas of Pyramids (pp. 319–324)
Find the surface area of the pyramid.
Question 40.
An
Question 41.
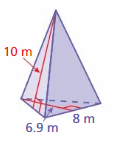
Answer:
The surface area of the pyramid = 95.2 m
Explanation:
The surface area of the square pymarid = area + (1/2) x ps
surface area = 55.2 + (1/2) x 10 x 8
surface area = 55.2 + 40
surface area = 95.2 m
Question 42.
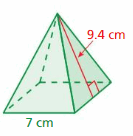
Answer:
The surface area of the pyramid = 88.1 cm
Explanation:
The surface area of the square pymarid = area + (1/2) x ps
surface area = 65.8 + (1/2) x 7 x 9.4
surface area = 55.2 + 32.9
surface area = 88.1 cm
Question 43.
You make a square pyramid for a school project. Find the surface area of the pyramid.
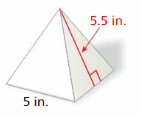
Answer:
The surface area of the pyramid = 41.25
Explanation:
The surface area of the square pyramid = area + (1/2) x ps
surface area = 27.5 + (1/2) x 5.5 x 5
surface area = 27.5 + 13.75
surface area = 41.25 in
7.7 Volumes of Rectangular Prisms (pp. 325–330)
Find volumes and missing dimensions of rectangular prisms.
Question 44.
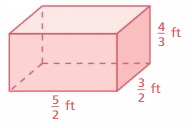
Answer:
The volume of rectangular prism = 4.875 ft
Explanation:
The volume of the rectangular prism = b ase x height
volume = b x h where b = l x w
volume = (5/2) x (3/2) x (4/3)
volume = 2.5 x 1.5 x 1.33
volume = 4.875 ft
Question 45.
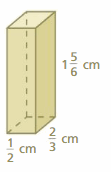
Answer:
The volume of rectangular prism = 0.605 cm
Explanation:
The volume of the rectangular prism = b ase x height
volume = b x h where b = l x w
volume = (1/2) x (2/3) x (11/6)
volume = 0.5 x 0.66 x 1.83
volume = 0.605 cm
Question 46.
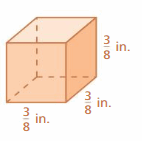
Answer:
The volume of rectangular prism = 0.05272 cu. in
Explanation:
The volume of the rectangular prism = b ase x height
volume = b x h where b = l x w
volume = (3/8) x (3/8) x (3/8)
volume = 0.375 x 0.375 x 0.375
volume = 0.05273 cu. in
Question 47.
The prism has a volume of 150 cubic feet. Find the length of the prism.
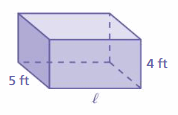
Answer:
The length of rectangular prism = 7 ft
Explanation:
The volume of the rectangular prism = base x height
volume = b x h where b = l x w
volume = (5) x (4) x (7)
volume = 150
length = 7 ft
Question 48.
How many cubic inches of tissues can the box hold?

Answer:
The length of rectangular prism = 162 . 5 in
Explanation:
The volume of the rectangular prism = b ase x height
volume = b x h where b = l x w
volume = (5) x (5) x (6.5)
volume = 162.5 in
Question 49.
Draw a rectangular prism that has a volume less than 1 cubic inch.
Area, Surface Area, and Volume Practice Test
7 Practice Test
Find the area of the figure.
Question 1.
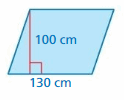
Answer:
The area of the parallelogram = 13000 cm
Explanation:
The area of the parallelogram = the product of the base and the product of the height
area = 130 x 100
area = 13000 cm
Question 2.
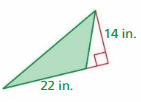
Answer:
The area of the triangle = 154 in
Explanation:
The area of the triangle = (1/2 ) x b x h
area = (1/2) x 14 x 22
area = (1/2) x 308
area = 154 in
Question 3.
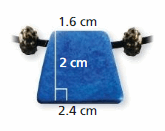
Find the surface area of the solid.
Question 4.
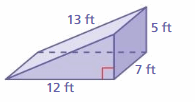
Answer:
340 ft
Explanation:
Surface area = area of the bottom + area of the front +area of the back +area of a side + area of a side
surface area = 12 x 7 = 84+ (1/2) x 7 x 5 = 17.5+ (1/2) x 7 x 5 = 17.5+ 13 x 5 = 65 + 12 x 13 = 156
bottom = 12 x 7 , front = (1/2) x 7 x 5, back = (1/2) x 7 x 5, side = 13 x 5 , side = 12 x 13
surface area = 84 + 17.5 +17.5 + 65+156
area = 340 ft
Question 5.
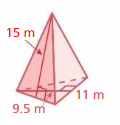
Answer:
The volume of the prism =1567.5 m
Explanation:
The volume of the prism = Bh where b = l x w
where b = area of the base
volume = (9.5) x(11) x (15)
volume = 1567.5 m
Find the volume of the prism.
Question 6.
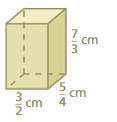
Answer:
The volume of the prism = 3.5 cm
Explanation:
The volume of the prism = b x h
volume = (3/2) x (7/3)
volume = 1.5 x 2.33
volume = 3.5 cm
Question 7.
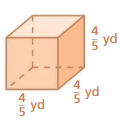
Answer:
The volume of the prism = 0.64 yd
Explanation:
The volume of the prism = b x h
volume = (4/5) x (4/5)
volume = 0.8 x 0.8
volume = 0.64 yd
Question 8.
Draw an octagonal prism.
Answer:

Question 9.
Find the numbers of faces, edges, and vertices of the solid.
Answer:
faces = 8
edges = 26
vertices = 10
Explanation:
The number of faces = 8
the number of edges = 26
the number of vertices = 10
Question 10.
The area of a parallelogram is 156 square meters. What is the height of the parallelogram when the base is 13 meters?
Answer:
The base of the parallelogram = 12 square meters
Explanation:
The area of the parallelogram = b x h
area = 13 x 12
area = 156
so base = 12 square meters
Question 11.
A candle is shaped like a square pyramid. Find the surface area of the candle.
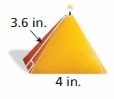
Answer:
The surface area of the candle = 21.6 in
Explanation:
The area of the square pyramid = area +(1/2) x p x s
surface area = 14.4 +(1/2) x 4 x 3.6
surface area = 14.4 + 7.2
surface area = 21.6 in
Question 12.
You are wrapping the boxed DVD collection as a present. What is the least amount of wrapping paper needed to wrap the box?

Question 13.
A cube has an edge length of 4 inches. You double the edge lengths. How many times greater is the volume of the new cube?
Answer:
2 times greater
Explanation:
Given that the cube has an edge length of 4 inches
They said to double the cube
4 x 2 = 8
the volume of the new cube is 2 times greater than that of the old cube
Question 14.
The Pentagon in Arlington, Virginia, is the headquarters of the U.S. Department of Defense. The building’s center contains a pentagon-shaped courtyard with an area of about 5 acres. Find the land areas (in square feet) of the courtyard and the building.
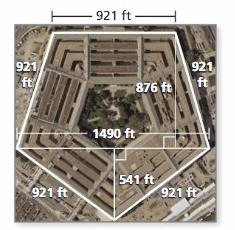
Area, Surface Area, and Volume Cumulative Practice
7 Cumulative Practice
Question 1.
A cruise ship is carrying a total of 4971 people. Each life boat can hold a maximum of 150 people. What is the minimum number of lifeboats needed to evacuate everyone on the cruise ship?
A. 33 lifeboats
B. 34 lifeboats
C. 54 lifeboats
D. 332 lifeboats
Answer:
option A is correct
Explanation:
150/33 = 4971 boats
In the above question, the lifeboat can hold a maximum of 150 people
The minimum no of lifeboats needed = 33

Question 2.
Which number is equivalent to the expression?
3 . 42 + 6 ÷ 2
F. 27
G. 33
H. 51
I. 75
Answer:
option H is correct
Explanation:
3 . 16 + 3
48 + 3
51
Question 3.
What is the volume of the package?
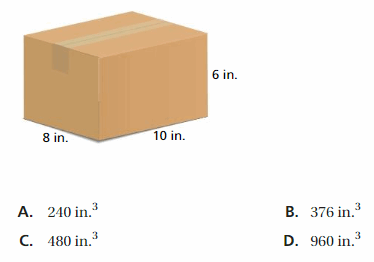
Question 4.
A housing community started with 60 homes. In each of the following years, 8 more homes were built. Let represent the number of years that have passed since the first year, and let n represent the number of homes. Which equation describes the relationship between n and y?
F. n = 8y + 60
G. n = 68y
H. n = 60y + 8
I. n = 60 + 8 + y
Answer:
option I is the correct
Explanation:
n = 60 + 8 + y
where n = no of homes
y = number of years
Question 5.
What is the value of m that makes the equation true?

4m = 6
Answer:
the value of m = (6/4)
Explanation:
m = (6/4)
4m = 6
4 x (6/4) = 6
6 = 6
Question 6.
What is the surface area of the square pyramid?
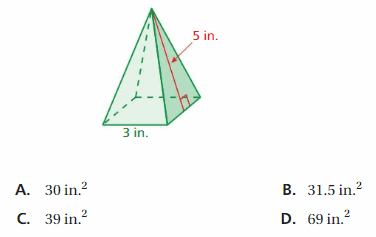
Answer:
none of the options are correct
Explanation:
surface area of the pyramid = area +(1/2)x(5x 3)
area = 15+ (1/2) (15)
area = 15 + 7.5
area = 22.5 in
Question 7.
A wooden box has a length of 12 inches, a width of 6 inches, and a height of 8 inches.

Part A
Draw and label a rectangular prism with the dimensions of the wooden box.
Part B
What is the surface area, in square inches, of the wooden box? Show your work.
Part C
You have a two-fluid ounce sample of wood stain that covers 900 square inches. Is this enough to give the entire box two coats of stain? Show your work and explain your reasoning.
Answer:
The surface area of the rectangular prism = 432 in
Explanation:
The surface area of the rectangular prism = Area of the top + area of the bottom +area of front + area of back + area of side + area of a side
surface area = 12 x 6 + 12 x 6 + 6 x 8 + 6 x 8 + 12 x 8+ 12 x 8
surface area = 72+ 72 + 48 + 48 + 96 +96
surface area = 432 in
a : 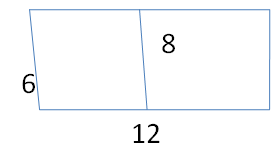
Question 8.
On Saturday, you earned $35 mowing lawns. This was dollars more than you earned on Thursday. Which expression represents the amount, in dollars, you earned mowing lawns on Thursday?
F. 35x
G. x + 35
H. x – 35
I. 35 – x
Answer:
Option G is correct
Explanation:
x + 35 is correct
Question 9.
What is the area, in square yards, of the triangle?
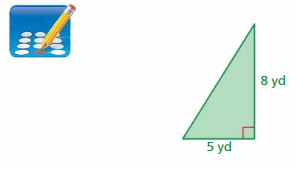
Answer:
The area of the triangle = 20 yd
Explanation:
Area of the triangle = (1/2) x b x h
area = (1/2) x 5 x 8 where b = 5 and h = 8 given
area = (1/2) x 40
area = 20yd
Question 10.
Which expression is equivalent to [latex]\frac{12}{35}\) ?

Answer:
option b is correct
Explanation:
(2 x 6)/(7 x 5)
12 / 35
so option b is correct
Question 11.
The description below represents the area of which polygon?

F. rectangle
G. parallelogram
H. trapezoid
I. triangle
Answer:
option h is correct
Explanation:
The formula of trapezoid = 0ne half the product of its height and the sum of its bases.
Question 12.
What is the missing quantity in the double number line?

A. 25 ounces
B. 165 ounces
C. 525 ounces
D. 600 ounces
Answer:
Option b is correct
Explanation:
6 + 15 = 21
150 + 15 = 165
so option b is correct
Conclusion:
I wish the details mentioned in the above article are helpful for you. Download Big Ideas Math Answers Grade 6 Chapter 7 Area, Surface Area, and Volume pdf for free of cost. Make use of the links and start solving the problems. Share the pdf link with your friends so that they can overcome the difficulties in grade 6 maths. Keep in touch with our page to get the solutions of all Big Ideas Math Grade 6 Chapters.