Free solutions to Big Ideas Math Grade 6 Chapter 3 Ratios and Rates are available here. So, the pupils those who are searching the Big Ideas Math Grade 6 Chapter 3 Ratios and Rates Solution Key can get them on this page. As per your convenience we have provided the solutions in the pdf format. So, Download Big Ideas Math Answers Grade 6 Chapter 3 Ratios and Rates pdf for free of cost.
Big Ideas Math Book 6th Grade Answer Key Chapter 3 Ratios and Rates
The list of topics covered in this chapter are Ratios, Using Tape Diagrams, Ratio tables, Graphing Ratio Relationships and so on. Check out the topics and practice the problems number of times and score highest marks in the exams. 6th Grade Ratios and Rates Solution Key helps the students to complete the homework or assignment in time.
Performance Task
Lesson: 1 Ratios
Lesson: 2 Using Tape Diagrams
Lesson: 3 Using Ratio Tables
Lesson: 4 Graphing Ratio Relationships
Lesson: 5 Rates and Unit Rates
Lesson: 6 Converting Measures
Performance Task
- Ratios and Rates Connecting Concepts
- Ratios and Rates Chapter Review
- Ratios and Rates Practice Test
- Ratios and Rates Cumulative Practice
Ratios and Rates STEAM Video/Performance Task
STEAM Video
Human Circulatory System
Watch the STEAM Video “Human Circulatory System.” Then answer the following questions.
1. Enid says the heart pumps about 5 liters of blood each minute. How can you find the amount of blood the heart pumps for any given number of minutes?
Answer:
Enid says the heart pumps about 5 liters of blood each minute.
5 × 1 = 5 liters
We have multiply number of minutes with 5
2. Explain how you can estimate the amount of blood your heart pumps in one heart beat.
Answer: Multiply your body surface area by the cardiac index to determine the liters of blood pumped by your heart in one minute.
3. The table shows the amounts of blood contained in several different types of blood vessels. How can you make meaningful comparisons of the amounts?
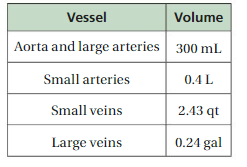
Answer:
1 liter = 1000 ml
The volume of Aorta and large arteries is 300 ml
300/1000 = 0.3 = 30%
Small arteries = 0.4L
0.4 × 1000 = 400ml = 40%
40% of blood contained in small arteries
Small veins = 2.43qt
2.43 qt = 2.299L
Large Veins = 0.24 gal
0.24 gal = 0.908L
Performance Task
Oops! Unit Conversion Mistakes
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be shown unit conversion mistakes in the following real-life situations.

In each situation, you will analyze and correct the mistake in the unit conversion. How accurate must conversions be in real-life situations?
Ratios and Rates Getting Ready for Chapter
Chapter Exploration
Work with a partner. What portion of the rectangle is red? How did you write your answer?
Question 1.
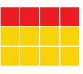
Answer: 4 : 12
Explanation:
Count the red portion shown in the image out of 12 potions
when we count we get Four-twelfths of the portion of the rectangle is red
Question 2.

Answer: 6 : 18
Explanation:
Count the red portion shown in the image out of 18 potion
when we count we get Six out of eighteen of the portion of the rectangle is red
Question 3.

Answer: 5 : 9
Explanation:
Count the red portion shown in the image out of 9 potion
when we count we get Five out of nine of the portion of the Square is red
Question 4.

Answer: 4 : 9
Explanation:
Count the red portion shown in the image out of 9 potion
when we count we get four out of nine of the portion of the Square is red
Question 5.

Answer: 6 : 9
Explanation:
Count the red portion shown in the image out of 9 potion
when we count we get six out of nine of the portion of the Square is red
Question 6.

Answer: 16 : 24
Explanation:
Count the red portion shown in the image out of 24 potion
when we count we get sixteen out of twenty-four of the portion of the Rectangle is red
Question 7.

Answer: 4 : 12
Explanation:
Count the red portion shown in the image out of 12 potion
when we count we get four out of twelve of the portion of the Rectangle is red
Question 8.
![]()
Answer: 5 : 12
Explanation:
Count the red portion shown in the image out of 12 potion
when we count we get five out of twelve of the portion of the Rectangle is red
Question 9.

Answer: 6 : 6
Explanation:
Count the red portion shown in the image out of 6 potion
when we count we get six out of six of the portion of the Rectangle is red
Question 10.
Work with a partner. In Exercises 1–9, which of the rectangles have the same portion of red tiles? Explain your reasoning.
Answer: 6 : 6 portion of the rectangles have the same portion of red tiles

Explanation:
Count the red portion shown in the image out of 6 potions
when we count we get six out of six of the portion of the Rectangle is red
Work with a partner. Use square color tiles to build two different-sized rectangles that represent the description.

Question 11.
Five-sixths of the tiles are blue.
Answer: 5 : 6
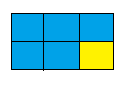
Explanation: a ratio indicates how many times one number contains another.
so 5 : 6 of the tiles are blue.
Question 12.
Three-fourths of the tiles are yellow.
Answer: 3 : 4
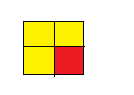
Explanation: a ratio indicates how many times one number contains another.
so 3 : 4 of the tiles are yellow
Question 13.
Four-fifths of the tiles are green.
Answer: 4 : 5
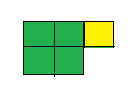
Explanation: a ratio indicates how many times one number contains another.
so 4 : 5 of the tiles are green
Question 14.
Five-sevenths of the tiles are red.
Answer: 5 : 7
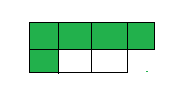
Explanation: a ratio indicates how many times one number contains another.
so 5 : 7 of the tiles are red
Question 15.
MODELING REAL LIFE
Work with a partner. The soccer committee has 8 girls and 6 boys. The tennis committee has 9 girls and 8 boys. A friend tells you that the tennis committee has a greater portion of girls than the soccer committee. Is your friend correct? Explain. If not, how many boys could you add to the soccer committee so that your friend is correct?
Answer:
Given,
The soccer committee has 8 girls and 6 boys. The tennis committee has 9 girls and 8 boys.
The ratio of soccer committee is 8:6
The ratio of tennis committee is 9:8
Compare both the ratios
8 < 9
Thus number of girls in tennis committee are more than soccer committee.
Thus we can say that your friend is correct.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.
ratio
rate
equivalent rates
equivalent ratios
unit rate
Answer:
Ratio – a ratio indicates how many times one number contains another.
Rate – a measure, quantity, or frequency, typically one measured against another quantity or measure.
Equivalent rates – Equivalent rates are rates that are equal.
Equivalent ratio – Two ratios that have the same value are called equivalent ratios.
Unit Rate – A unit rate is a rate with 1 in the denominator.
Lesson 3.1 Ratios
A ratio is a comparison of two quantities. Consider two quantities a and b. The ratio a : b indicates that there are a units of the first quantity for every b units of the second quantity.
EXPLORATION 1
Writing Ratios
Work with a partner. A science class has two times as many girls as it has boys.

a. Discuss possible numbers of boys and girls in the science class.
Answer: 24 girls and 12 boys in the science class
b. What comparisons can you make between your class and the science class? Can you determine which class has more girls? more boys? Explain your reasoning.
Answer:
Number of girls and boys in your class are 42.
Number of girls = 22
Number of boys = 20
Compare the number of girls in your class and science class
22: 24
Thus there are more girls in science class.
20:12
Thus there are more boys in your class.
c. Write three ratios that you observe in your classroom. Describe what each ratio represents.
Answer:
36:42 – This represents number of students in science class and your class
22:24 – This represents number of girls in science class and your class
20:12 – This represents number of boys in science class and your class
EXPLORATION 2
Using Ratios in a Recipe
Work with a partner. The ratio of iced tea to lemonade in a recipe is 3 : 1. You begin by combining 3 cups of iced tea with 1 cup of lemonade.

a. You add 1 cup of iced tea and 1 cup of lemonade to the mixture. Does this change the taste of the mixture?
Answer:
3 + 1: 1 + 1
4:2
No it will not change the taste of the mixture.
b. Describe how you can make larger amounts without changing the taste.
Answer: If the number of portions and the size of each portion change, you will have to find a conversion factor using a similar approach.

Try It
Write the indicated ratio using the coins in Example 1.
Question 1.
dimes to pennies
Answer: 1 : 10
Explanation:
we have to convert the coins from dimes to pennies.
we know that A dime is worth 10 pennies.
so the ratio is 1 : 10
Question 2.
quarters to the total number of coins.
Answer: 25 : 40
The number \(\frac{a}{b}\) associated with the ratio a : b is called the value of the ratio. It describes the multiplicative relationship between the quantities in a ratio.
Question 3.
An elephant sanctuary contains adult and baby elephants. The ratio of adult elephants to baby elephants is 5 : 1. Find and interpret the value of the ratio.

Answer: five adult elephants and one baby elephant
Determine whether the ratios are equivalent.
Question 4.
1 : 1 and 6 : 6
Answer: The ratios are Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 1 : 1 and 6 : 6 are Equivalent
Question 5.
1 : 2 and 3 : 4
Answer: The ratios are Not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
hence the 1 : 2 and 3 : 4 The ratios are Not Equivalent.
Question 6.
8 : 3 and 6 : 16
Answer: The ratios are Not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
hence the 8 : 3 and 6 : 16 ratios are Not Equivalent.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
WRITING AND INTERPRETING RATIOS Write the ratio. Then find and interpret the value of the ratio.

Question 7.
sharks to dolphins
Answer: 4 : 5
Explanation: a ratio indicates how many times one number contains another.
so 4 : 5 of sharks to dolphins by observing the picture given
Question 8.
dolphins : animals
Answer: 5 : 0
Explanation: a ratio indicates how many times one number contains another.
so 5 : 0 of dolphins: animals by observing the picture given
IDENTIFYING EQUIVALENT RATIOS Determine whether the ratios are equivalent. Explain your reasoning.
Question 9.
2 : 3 and 24 : 36
Answer: The ratios are Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 2 : 3 and 24 : 36 are Equivalent
Question 10.
5 : 7 and 20 : 28
Answer: The ratios are Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 5 : 7 and 20 : 28 are Equivalent
Question 11.
3 : 10 and 9 : 25
Answer: The ratios are Not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
hence the 3 : 10 and 9 : 25 ratios are Not Equivalent.
Question 12.
DIFFERENT WORDS, SAME QUESTION Which is different? Find “both” answers.

Answer:
Option B and C has same question but different words.
Question 13.
The ratio of wolves to cougars in a forest is 5 : 3. Find and interpret the value of the ratio.

Answer: 5 to 3
Explanation: A ratio takes one number and divides it into another number to determine a decimal that can later be converted to a percentage if desired The ratio of wolves to cougars in a forest is 5 : 3 so the interpret the value of the ratio is 5 to 3.
Question 14.
You are kayaking at a pace of 63 feet every 12 seconds. Your friend’s pace is 21 feet every 3 seconds. Are you and your friend kayaking at the same pace? If not, who is faster?
Answer: No, Me and my friend kayaking are not at the same pace. my friend is faster.
Explanation:
Given,
You are kayaking at a pace of 63 feet every 12 seconds
Your friend’s pace is 21 feet every 3 seconds
So if I am kayaking at apace of 63 feet for every 12 seconds. then dividing 63 feet by 12 seconds we get 5.25 feet per second.
In the same way friend’s pace is 21 feet every 3 seconds. the dividing 21 feet by 3 second we get 7 feet per second.
Hence me and my friend are not at the same pace.
7 feet per second my friend is faster than me
Question 15.
DIG DEEPER!
The ratio of Jet Ski rentals to boat rentals at a store is 7 : 2. If the number of boat rentals doubles and the number of Jet Ski rentals stays the same, then the number of boat rentals is how many times the number of Jet Ski rentals?

Answer: 0.571 times less than jet Ski rental
Given,
he ratio of Jet Ski rentals to boat rentals at a store is 7 : 2
If the number of boat rentals doubles then we get 2 × 2 = 4 boats
the number of Jet Ski rentals stays the same that is 7
then the number of boat rentals is how many times the number of Jet Ski rental is divide 4 by 7 we get 0.571 times less than jet Ski rental
Ratios Homework & Practice 3.1
Review & Refresh
Divide. Check your answer.
Question 1.
15.4 ÷ 2.2
Answer: 7
Explanation:
Given 15.4 ÷ 2.2
so divide 15.4 by 2.2 we get 7
Question 2.
56.07 ÷ 8.9
Answer: 6.9
Explanation:
Given 56.07 ÷ 8.9
so divide 56.07 by 8.9 we get 6.9
Question 3.
\(\sqrt [ 8.43 ]{ 12.645 } \)
Answer: 0.8164
Explanation:
Given \(\sqrt [ 8.43 ]{ 12.645 } \)
so divide square root of 8.43 by 12.645 we get 0.8164
Question 4.
\(\sqrt [ 11.6 ]{ 51.62 } \)
Answer: 0.474
Explanation:
Given \(\sqrt [ 11.6 ]{ 51.62 } \)
so divide square root of 11.6 by 51.62 we get 0.474
Find the value of the power.
Question 5.
82
Answer: 8 × 8 = 64
Explanation:
given 82
so by multiplying 8 × 8, we get 64
Question 6.
16
Answer: 1
Explanation:
given 1 power of 6
so by multiplying 1 × 1 × 1 ×1 × 1 × 1 we get 1
Question 7.
34
Answer: 81
Explanation:
given 3 power of 4
so by multiplying 3 × 3 × 3 × 3 we get 81
Question 8.
26
Answer: 64
Explanation:
given 2 power of 6
so by multiplying 2 × 2 × 2 ×2 × 2 × 2 we get 64
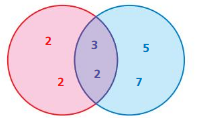
The Venn diagram shows the prime factors of two numbers. Identify the numbers. Then find the GCF and the LCM of the two numbers.
Question 9.
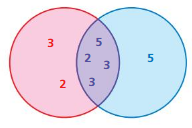
Answer:
By using the venn diagram we can find the prime factors of the two numbers.
2 × 2 × 3 × 3 × 3 × 5 = 540
2 × 3 × 3 × 5 × 5 = 450
LCM of 540 and 450 are
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 450:
450, 900, 1350, 1800, 2250, 2700, 3150, 3600
Multiples of 540:
540, 1080, 1620, 2160, 2700, 3240, 3780
Therefore,
LCM(450, 540) = 2700
GCF of 540 and 450 are
The factors of 450 are: 1, 2, 3, 5, 6, 9, 10, 15, 18, 25, 30, 45, 50, 75, 90, 150, 225, 450
The factors of 540 are: 1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 27, 30, 36, 45, 54, 60, 90, 108, 135, 180, 270, 540
Then the greatest common factor is 90.
Question 10.
Answer:
By using the venn diagram we can find the prime factors of the two numbers.
2 × 2 × 2 × 3 = 24
2 × 3 × 5 × 7 = 210
LCM of 24 and 210:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 24:
24, 48, 72, 96, 120, 144, 168, 192, 216, 240, 264, 288, 312, 336, 360, 384, 408, 432, 456, 480, 504, 528, 552, 576, 600, 624, 648, 672, 696, 720, 744, 768, 792, 816, 840, 864, 888
Multiples of 210:
210, 420, 630, 840, 1050, 1260
Therefore,
LCM(24, 210) = 840
GCF of 24 and 210:
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
The factors of 210 are: 1, 2, 3, 5, 6, 7, 10, 14, 15, 21, 30, 35, 42, 70, 105, 210
Then the greatest common factor is 6.
Concepts, Skills, & Problem Solving
USING RATIOS You mix the amounts of iced tea and lemonade shown. Describe how you can make larger amounts without changing the taste. (See Exploration 2, p. 107.)
Question 11.

Answer:
There are 2 iced tea and 1 lemonade.
So, we can make 2:1 iced tea and lemonade without changing the taste.
Question 12.

Answer: 2:3
There are 2 iced tea and 3 lemonade.
So, we can make 2:3 iced tea and lemonade without changing the taste.
WRITING RATIOS Write the ratio.
Question 13.
frogs to turtles

Answer: 2 : 5
Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b.
There are two frogs and five turtles in the shown image.
hence frogs to turtles is 2 : 5
Question 14
basketballs to soccer balls

Answer: 6 : 4
Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b.
There are six basketballs and four soccer balls in the shown image.
hence basketballs to soccer balls are 6 : 4
Question 15.
calculators : pencils

Answer: 2 : 6
Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b.
There are two calculators and six pencils in the shown image.
hence calculators : pencils are 2 : 6
Question 16.
shirts : pants

Answer: 3 : 6
Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b.
There are three shirts and six pants in the shown image.
hence shirts : pants are 3 : 6
Question 17.
MODELING REAL LIFE
Twelve of the 28 students in a class own a dog. What is the ratio of students who own a dog to students who do not?
Answer: 12 : 28
Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b.
Given Twelve of the 28 students in a class own a dog we get 12 students who have dogs out of 28 students
so in the students who do not have dogs are 28
hence the ratio of students who own a dog to students who do not is 12 : 28
Question 18.
LOGIC
Name two things that you would like to have in a ratio of 5 : 1 but not in a ratio of 1 : 5. Explain your reasoning.
Answer:
5 students in 1 class gives the ratio 5:1
It is not possible to have 1 student in 5 classes.
OPEN-ENDED Describe a real-life relationship that can be represented by the ratio.
Question 19.
1 out of every 7
Answer: 1 : 7
Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b.
hence 1 out of every 7 is 1 : 7
Question 20.
5 to 26
Answer: 5 : 26
Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b.
hence 5 to 26 7 is 5 : 26
Question 21.
2 per 5
Answer: 2 : 5
Explanation: A ratio shows how much of one thing there is compared to another. Ratios are usually written in the form a:b.
hence 2 per 5 is 2 : 5
Question 22.
7 : 1
Answer: 7 out of 1
Explanation: a ratio indicates how many times one number contains another.
Hence 7 : 1 is 7 out of 1
Question 23.
MODELING REAL LIFE
During a given month, the ratio of sunny days to rainy days is 4 : 1.
a. Find and interpret the value of the ratio.
Answer:
Let us consider the month be April
The number of days in April are 30.
4:1
4 × 6 = 24 days
1 × 6 = 6 days
24 + 6 = 30 days
b. In another month, the number of sunny days is 5 times the number of rainy days. Write the ratio of sunny days to rainy days.
Answer: 5:1
Explanation:
Given,
In another month, the number of sunny days is 5 times the number of rainy days.
The ratio of the sunny days to rainy days is 5 : 1
IDENTIFYING EQUIVALENT RATIOS Determine whether the ratios are equivalent.
Question 24.
2 : 3 and 4 : 9
Answer: The ratios are Not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 2 : 3 and 4 : 9 are Not Equivalent
Question 25.
3 : 8 and 9 : 24
Answer: The ratios are Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 3 : 8 and 9 : 24 are Equivalent
Question 26.
1 : 4 and 2 : 6
Answer: The ratios are Not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 1 : 4 and 2 : 6 are Not Equivalent
Question 27.
5 : 3 and 15 : 12
Answer: The ratios are Not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 5 : 3 and 15 : 12 are Not Equivalent
Question 28.
6 : 10 and 12 : 20
Answer: The ratios are Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 6 : 10 and 12 : 20 are Equivalent.
Question 29.
2 : 3 and 4 : 5
Answer: The ratios are not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 2 : 3 and 4 : 5 are not Equivalent.
Question 30.
28 : 32 and 7 : 8
Answer: The ratios are Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 28 : 32 and 7 : 8 are Equivalent.
Question 31.
24 : 100 and 6 : 25
Answer: The ratios are Not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 28 : 32 and 7 : 8 are Not Equivalent.
Question 32.
85 : 210 and 340 : 735
Answer: The ratios are Not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 85 : 210 and 340 : 735 are Not Equivalent.
WRITING EQUIVALENT RATIOS Write a ratio that is equivalent to the given ratio. Justify your answer.
Question 33.
3 : 1
Answer: 6: 2
Explanation:
The equivalent ratio of 3:1 is 6:2
Two ratios that have the same value are called equivalent ratios.
6:2 = 3:1
Question 34.
7 : 2
Answer: 14: 4
Explanation:
Two ratios that have the same value are called equivalent ratios.
The equivalent ratio of 7 : 2 is 14:4
7 × 2 : 2 × 2 = 14:4
Question 35.
6 : 6
Answer: 12:12
Explanation:
Two ratios that have the same value are called equivalent ratios.
The equivalent ratio of 6:6 is 12:12
6 × 2 : 6 × 2 = 12:12
Question 36.
0 : 8
Answer: 0:16
Explanation:
Two ratios that have the same value are called equivalent ratios.
The equivalent ratio of 0:8 is 0:16
0 × 2: 8 × 2 = 0 : 16
WRITING EQUIVALENT RATIOS Fill in the blank so that the ratios are equivalent.
Question 37.
![]()
Answer: 18
![]()
Explanation:
Since
3 : 9 = 6 : X
Then we know
9/3 = X/6
Multiplying both sides by 6 cancels on the right
6 × (9/3) = (X/6) × 6
6 × (9/3) = X
Then solving for X
X = 6 × (9/3)
X = 18
Therefore
3 : 9 = 6 : 18
Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Question 38.
![]()
Answer: 24
![]()
Explanation:
Since
2 : 6 = 8 : X
Then we know
6/2 = X/8
Multiplying both sides by 8 cancels on the right
8 × (6/2) = (X/8) × 8
8 × (6/2) = X
Then solving for X
X = 8 × (6/2)
X = 24
Therefore
2 : 6 = 8 : 24
Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Question 39.
![]()
Answer: 21
![]()
Explanation:
Since
X : 6 = 7 : 2
Then we know
X/6 = 7/2
Multiplying both sides by 6 cancels on the left
6 × (X/6) = (7/2) × 6
X = (7/2) × 6
Then solving for X
X = 6 × (7/2)
X = 21
Therefore
21 : 6 = 7 : 2
Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Question 40.
YOU BE THE TEACHER
Your friend says that the two ratios are equivalent. Is your friend correct? Explain your reasoning.

Answer: incorrect, The ratios are Not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 4 : 8 and 8 : 12 are Not Equivalent. after add 4 each to the ratios
Question 41.
OPEN-ENDED
A non-Newtonian liquid demonstrates properties of both a solid and a liquid. A recipe for a non-Newtonian liquid calls for 1 cup of water and 2 cups of cornstarch. Find two possible combinations of water and cornstarch that you can use to make a larger batch. Justify your answer.
Answer:
Given,
A non-Newtonian liquid demonstrates properties of both a solid and a liquid.
A recipe for a non-Newtonian liquid calls for 1 cup of water and 2 cups of cornstarch
The ratio of water and cornstarch is 1 : 2
The possible combinations of water and cornstarch are
You can multiply 3 to each number in the first ratio to obtain the numbers in the second ratio, the ratios are equivalent.
1 × 3 : 2 × 3 = 3 : 6
You can multiply 5 to each number in the first ratio to obtain the numbers in the second ratio, the ratios are equivalent.
1 × 5 : 2 × 5 = 5 : 10
Question 42.
PROBLEM SOLVING
You are downloading songs to your tablet. The ratio of pop songs to rock songs is 5 : 4. You download 40 pop songs. How many rock songs do you download?
Answer: 32
Explanation:
Given,
. The ratio of pop songs to rock songs is 5 : 4. You download 40 pop songs.
Let number of rock songs be x
5 : 4 :: 40 :: x
5 × x = 4 × 40
5x = 160
x = 160/5
x = 32
Therefore, number of rock songs = 32.
Question 43.
PROBLEM SOLVING
In the contiguous United States, the ratio of states that border an ocean to states that do not border an ocean is 7 : 9. How many of the states border an ocean?
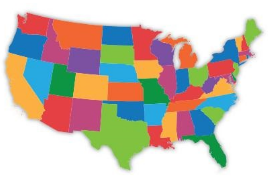
Answer: 7
Explanation:
Given,
the ratio of states that border an ocean to states that do not border an ocean is 7 : 9.
So states that border an ocean is 7
and states that do not border an ocean is 9
hence the states border an ocean is 7
Question 44.
REASONING
The value of a ratio is \(\frac{4}{3}\). The second quantity in the ratio is how many times the first quantity in the ratio? Explain your reasoning.
Answer: The second quantity is 1.3333 times the first quantity in the ratio.
Explanation:
A ratio is given to us which is 4:3.
What we need to find out is, the second quantity in the ratio is how many times the first quantity in the ratio.
The definition of ratio is, the quantitative relation between two amounts showing the number of times one value contains or is contained within the other.
So according to the definition of ratio we get:
4/3 = 1.33
So we can say that 4 contains 3, 1.3333 times in it.
So the second quantity is 1.3333 times the first quantity in the ratio.
Question 45.
MODELING REAL LIFE
A train moving at a constant speed travels 3 miles every 5 minutes. A car moving at a constant speed travels 12 miles every 20 minutes. Are the vehicles traveling at the same speed? If not, which is faster?

Answer:
Both vehicles traveling at the same speed 0.6 miles per minute
Explanation:
Given
A train moving at a constant speed travels 3 miles every 5 minutes.
by dividing 3 miles by 5 minutes we get 0.6 miles per minute
A car moving at a constant speed travels 12 miles every 20 minutes.
by dividing 12 miles by 20 minutes we get 0.6 miles per minute
Hence both vehicle have the same speed
Question 46.
CRITICAL THINKING
To win a relay race, you must swim 200 yards before your opponent swims 190 yards. You swim at a pace of 50 yards every 40 seconds. Your opponent swims at a pace of 10 yards every 8.5 seconds. Who wins the race? Justify your answer.
Answer:
Explanation:
Given
You swim at a pace of 50 yards every 40 seconds
By dividing 50 yards by 40 seconds we get 1.25 yards per second
Your opponent swims at a pace of 10 yards every 8.5 seconds.
By dividing 10 yards by 8.5 seconds we get 1.17 yards per second
You swim at a pace of 50 yards every 40 seconds for completing 200 yards you take 160 seconds
your opponent swims at a pace of 10 yards every 8.5 seconds for completing 190 yards you take 162.3 seconds
hence you won the race by completing 200 yards in 160 seconds before your opponent completes 190 yards at 162.3 seconds
Question 47.
DIG DEEPER!
There are 3 boys for every 2 girls in a dance competition. Does it make sense for there to be a total of 9 people in the competition? Explain.
Answer: No
Explanation:
Given,
There are 3 boys for every 2 girls in a dance competition.
3:2=5
so girls are 2:5
set up the proportion
2/5=x/9
5x=18
x=3.6 girls
another way you can look at it is because there are 3 boys for every 2 girls, add 2 more girls, you’ll get 3 more boys
that makes the total of 10 people so 9 is impossible
Question 48.
GEOMETRY
Use the blue and green rectangles.
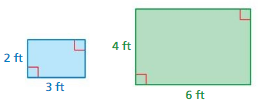
a. Find the ratio of the length of the blue rectangle to the length of the green rectangle. Repeat this for width, perimeter, and area.
Answer:
The ratio of the length of the blue rectangle to the length of the green rectangle is 2 : 4
The ratio of the width of the blue rectangle to the width of the green rectangle is 3 : 6
Perimeter of the rectangle = 2l + 2w
Blue rectangle:
2(3) + 2(2) = 6 + 4 = 10
Green Rectangle:
2(6) + 2(4) = 12 + 8 = 20
Ratio of perimeter of blue rectangle to the green rectangle is 10 : 20
Area of the rectangle = lb
Blue rectangle:
A = 2 × 3 = 6
Green Rectangle:
A = 4 × 6 = 24
Ratio of Area of blue rectangle to the green rectangle is 6 : 24
b. Compare your ratios in part(a).
Answer:
The ratio of the length of the blue rectangle to the length of the green rectangle is 2 : 4 equivalent to 1 : 2
The ratio of the width of the blue rectangle to the width of the green rectangle is 3 : 6 equivalent to 1 : 2
Ratio of perimeter of blue rectangle to the green rectangle is 10 : 20 equivalent to 1 : 2
Ratio of Area of blue rectangle to the green rectangle is 6 : 24 equivalent to 1 : 4
Question 49.
STRUCTURE
The ratio of the side lengths of a triangle is 2 : 3 : 4. The shortest side is 15 inches. What is the perimeter of the triangle? Explain.
Answer: 67.5 inches
Explanation:
Given that,
The ratio of the side lengths of a triangle is 2 : 3 : 4. The shortest side is 15 inches.
Let
x = the first side
y = the second side
z = the third side
We know that
x/y = 2/3
y = 1.5x
x/z = 2/4
z = 2x
x = 15 inches
Substitute the value of x in both the equations
y = 1.5(15) = 22.5 in
z = 2(15) = 30 in
Now find the perimeter of the triangle
P = x + y + z
P = 15 + 22.5 + 30 = 67.5 inches
Question 50.
PROBLEM SOLVING
A restaurant sells tokens that customers use to play games while waiting for their orders.

a. Which option is the best deal? Justify your answer.
b. What suggestions, if any, would you give to the restaurant about how it could modify the prices of tokens?
Answer:
It would be 90 tokens
0.50 * 10 = $5
0.50 *25 = $12.5
0.50 * 50 = $25
0.50 * 90 = $45
on 90 tokens you save $5 which is the most.
Question 51.
DIG DEEPER!
There are 12 boys and 10 girls in your gym class. If 6 boys joined the class, how many girls would need to join for the ratio of boys to girls to remain the same? Justify your answer.
Answer:
Given,
There are 12 boys and 10 girls in your gym class.
12/10=6/5
6 boys joined: 18/(of girls)=6/5, #of girls=18×5/6=15
5 more girls will keep the same ratio 6/5
Lesson 3.2 Using Tape Diagrams
You can use a visual model, called a tape diagram, to represent the relationship between two quantities in a ratio.
EXPLORATION 1
Using a Tape Diagram
Work with a partner. The tape diagram models the lengths of two snowboarding trails.
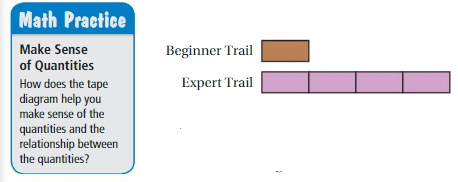
a. What can you determine from the tape diagram?
Answer:
We determine from the tape diagram that the beginner trail has one rectangle and the expert trial has four rectangles.
b. Choose a length for one of the trails. What conclusions can you make from the tape diagram? Explain your reasoning.
Answer:
Let the length of one rectangle is 10.
The length of the beginner trail is 10.
Length of the expert trail is 4 × 10 = 40
1 : 4
c. Suppose you know the combined length of the trails or the difference in the lengths of the trails. Explain how you can use that information to find the lengths of the two trails. Provide an example with your explanation.

Answer:
Let the length of one rectangle is 10.
Now let us combine the length to find the length of the expert trail.
The expert trail contains 4 rectangles.
So, multiply 10 with 4.
4 × 10 = 40
Example:
The tape diagram represents the ratio of gifts received to gifts given. You received 4 gifts.
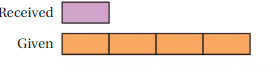
You can use tape diagrams to represent ratios and solve ratio problems.
Try It
Question 1.
The tape diagram represents the ratio of gifts received to gifts given. You received 4 gifts. How many gifts did you give?

Answer: 1 : 4
Explanation:
given
The tape diagram represents the ratio of gifts received to gifts given.
You received 4 gifts
the ratio by observing the given image is 1 : 4
hence you gave 1 gift
Question 2.
There are 8 bones in a large snake for every 3 bones in a small snake. The small snake has 150 bones. How many bones does the large snake have?
Answer: 400
Explanation:
Given,
There are 8 bones in a large snake for every 3 bones in a small snake.
The small snake has 150 bones.
150/3 = 50 bones
50 × 8 = 400 bones
Thus the large snake has 400 bones.
Question 3.
WHAT IF?
Repeat Example 3 when the ratio of your monthly allowance to your friend’s monthly allowance is 2 to 3.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
STRUCTURE
What ratio is represented by the tape diagram? Can you use the tape diagram to model the ratio 6 : 9? Can you use the tape diagram to model the ratio 8 : 16? Explain your reasoning.
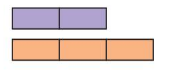
Answer:
Question 5.
REASONING
You are given a tape diagram and the total value of the parts. How can you find the value of 1 part?
Answer:
Question 6.
DRAWING A TAPE DIAGRAM
Describe two ways that you can represent the ratio 12 : 4 using a tape diagram.
Answer:
USING A TAPE DIAGRAM You are given the number of tickets in a bag and the ratio of winning tickets to losing tickets. How many of each kind of ticket are in the bag?

Question 7.
35 tickets; 1 to 4
Answer: 7 : 28
Explanation:
Number of winning tickets = 7
Number of losing tickets = 28
The ratio of winning tickets and losing tickets are 7 : 28
We get 1 : 4
Thus the answer is 7 : 28
Question 8.
80 tickets; 2 : 8
Answer: 16 : 64
Explanation:
Total number of tickets = 80
The ratio of winning tickets to losing tickets is 2 : 8
Let 2x be the winning tickets and 8x be the losing tickets
2x + 8x = 80
10x = 80
x = 80/10 = 8
Number of winning tickets = 2x = 2(8) = 16
Number of losing tickets = 8x = 8(8) = 64
The ratio of winning tickets and losing tickets are 16 : 64
Question 9.
The tape diagram represents the ratio of the numbers of planets in two different solar systems. There are 8 planets in Solar System B. How many planets are in Solar System A?
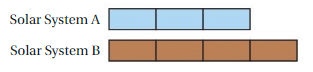
Answer:
The ratio of the numbers of planets in two different solar systems is 3 : 4
Given that
There are 8 planets in Solar System B.
Solar System B contains 4 rectangles
4 × 2 = 8
Solar System A contains 3 rectangles
3 × 2 = 6
Therefore the solar system A contains 6 planets.
Question 10.
You and your friend play an arcade game. You score 5 points for every 9 points that your friend scores. You score 320 points less than your friend. How many points do you each score?

Answer:
Given
You and your friend play an arcade game.
You score 5 points for every 9 points that your friend scores.
You score 320 points less than your friend.
Each time you score you gain 4 less points than your friend so, you can do this equation
9x – 320 = 5x
9x – 5x = 320
4x = 320
x = 320/4
x = 80
9x = 9(80) = 720
5x = 5(80) = 400
720 – 400 = 320
Question 11.
DIG DEEPER!
Your team wins 18 medals at a track meet. The medals are gold, silver, and bronze in a ratio of 2 : 2 : 5. How many of each medal were won by your team?
Answer: The team won 4 gold medals, 4 silver medals and 10 bronze medals.
Explanation:
Given,
Total medals won = 18
Ratio of gold, silver and bronze = 2:2:5
Let,
x be the original number.
Therefore,
Gold medals = 2x
Silver medals = 2x
Bronze medals = 5x
According to given statement
2x + 2x + 5x = 18
9x = 18
x = 2
Gold medals = 2x = 2(2) = 4
Silver medals = 2x = 2(2) = 4
Bronze medals = 5x = 5(2) = 10
Using Tape Diagrams Homework & Practice 3.2
Review & Refresh
Determine whether the ratios are equivalent.
Question 1.
11 : 4 and 22 : 8
Answer: The ratios are Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 11 : 4 and 22 : 8 are Equivalent.
Question 2.
12 : 18 and 2 : 3
Answer: The ratios are Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 12 : 18 and 2 : 3 are Equivalent.
Question 3.
56 : 81 and 7 : 9
Answer: The ratios are not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 56 : 81 and 7 : 9 are not Equivalent.
Question 4.
2 : 12 and 6 : 24
Answer: The ratios are not Equivalent.
Explanation: Two ratios that have the same value are called equivalent ratios. To find an equivalent ratio, multiply or divide both quantities by the same number. It is the same process as finding equivalent fractions. Multiply both the numerator and denominator by 2.
Hence the ratios 2 : 12 and 6 : 24 are not Equivalent.
Multiply. Write the answer in the simplest form.
Question 5.
\(\frac{7}{10}\) . \(\frac{5}{7}\)
Answer: \(\frac{1}{2}\)
For fraction multiplication, multiply the numerators and then multiply the denominators to get
\(\frac{7}{10}\) . \(\frac{5}{7}\)
This fraction can be reduced by dividing both the numerator and denominator by the Greatest Common Factor of 35 and 70 using
GCF(35,70) = 35
35÷35 divided by 70÷35= \(\frac{1}{2}\)
Therefore:
\(\frac{7}{10}\) . \(\frac{5}{7}\) is 12
Question 6.
2\(\frac{1}{3}\) . \(\frac{3}{4}\)
Answer: \(\frac{1}{2}\)
Explanation:
For fraction multiplication, multiply the numerators and then multiply the denominators to get
1×33×4=312
This fraction can be reduced by dividing both the numerator and denominator by the Greatest Common Factor of 3 and 12 using
GCF(3,12) = 3
3÷3 divided by 12÷3= \(\frac{1}{4}\)
Therefore:
as given in question 2\(\frac{1}{3}\) . \(\frac{3}{4}\) = 2 × \(\frac{1}{4}\)
we get \(\frac{1}{2}\)
Question 7.
5\(\frac{3}{8}\) . 2\(\frac{1}{2}\)
Answer: 13 \(\frac{7}{16}\)
Explanation:
Convert any mixed numbers to fractions.
5\(\frac{3}{8}\) = \(\frac{43}{8}\)
2\(\frac{1}{2}\) = \(\frac{5}{2}\)
\(\frac{43}{8}\) × \(\frac{5}{2}\) = \(\frac{215}{16}\)
Now convert it into the mixed fractions
\(\frac{215}{16}\) = 13 \(\frac{7}{16}\)
Question 8.
Melissa earns $7.40 per hour working at a grocery store. She works 14.25 hours this week. How much does she earn?
A. $83.13
B. $105.45
C. $156.75
D. $1054.50
Answer: $105.45
Explanation:
Given,
Melissa earns $7.40 per hour working at a grocery store.
She works 14.25 hours this week.
14.25 × 7.40 = $105.45
Thus Melissa earns $105.45 this week
Concepts, Skills, & Problem Solving
USING A TAPE DIAGRAM Use the tape diagram in Exploration 1 to answer the question. (See Exploration 1, p. 115.)

Question 9.
The beginner trail is 200 meters long. How long is the expert trail?
Answer:
For the beginner’s trail, there is only one rectangle. For Expert Trail, there are 4 rectangles.
Then in total, we have 5 rectangles.
We know that the combined length is 200 meters, then the 5 rectangles are equivalent to 200 meters.
Then each rectangle will be equivalent to:
200m/5 = 40m.
Now, we know that the beginner’s trail has one rectangle, then the length of the beginner’s trail is 40 meters long.
The expert’s trail has 4 rectangles, then it is:
4×40m = 160m long.
Question 10.
The expert trail is 1200 meters long. How long is the beginner trail?
Answer:
For the beginner’s trail, there is only one rectangle. For Expert Trail, there are 4 rectangles.
Then in total, we have 5 rectangles.
We know that the combined length is 1200 meters, then the 5 rectangles are equivalent to 1200 meters.
Then each rectangle will be equivalent to:
1200m/5 = 240m
Now, we know that the beginner’s trail has one rectangle, then the length of the beginner’s trail is 240 meters long.
The expert’s trail has 4 rectangles, then it is:
4×240m = 960m long.
Question 11.
The combined length of the trails is 2000 meters. How long is each trail?
Answer:
For the beginner’s trail, there is only one rectangle. For Expert Trail, there are 4 rectangles.
Then in total, we have 5 rectangles.
We know that the combined length is 2000 meters, then the 5 rectangles are equivalent to 2000 meters.
Then each rectangle will be equivalent to:
2000m/5 = 400m.
Now, we know that the beginner’s trail has one rectangle, then the length of the beginner’s trail is 400 meters long.
The expert’s trail has 4 rectangles, then it is:
4×400m = 1600m long.
Question 12.
The expert trail is 750 meters longer than the beginner trail. How long is each trail?
Answer:
For the beginner’s trail, there is only one rectangle. For Expert Trail, there are 4 rectangles.
Then in total, we have 5 rectangles.
We know that the combined length is 750 meters, then the 5 rectangles are equivalent to 750 meters.
Then each rectangle will be equivalent to:
750m/5 = 150m
Now, we know that the beginner’s trail has one rectangle, then the length of the beginner’s trail is 150 meters long.
The expert’s trail has 4 rectangles, then it is:
4×150m = 600m long.
INTERPRETING A TAPE DIAGRAM The tape diagram represents the ratio of the time you spend tutoring to the time your friend spends tutoring. You tutor for 3 hours. How many hours does your friend spend tutoring?
Question 13.
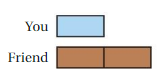
Answer:
So you have one block, and your friend has two.
We know that you work for 3 hours, this means that your only block must represent 3 hours.
And all the blocks represent the same amount of time, then each one of the two blocks of your friend also represents 3 hours.
Then in total, he tutored for 3 hours + 3 hours = 6 hours.
Question 14.
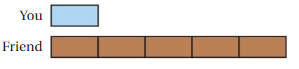
Answer:
In this case, you still have only one block, but now your friend has 5.
Using the same reasoning as above, we can conclude that each block represents 3 hours, and your friend has 5 of them
this means that he tutored for:
5×3 hours = 15 hours
DRAWING A TAPE DIAGRAM A bag contains red marbles and blue marbles. You are given the number of red marbles in the bag and the ratio of red marbles to blue marbles. Find the number of blue marbles in the bag.
Question 15.
10 red marbles; 5 to 1
Answer:
red : blue=5:1
red/blue=5
red= 10
so blue= 2
Question 16.
3 red marbles; 3 : 7
Answer:
red : blue=3:7
red/blue=3/7
red= 3
so blue= 7
Question 17.
12 red marbles; 4 : 3
Answer:
red : blue=4:3
red/blue= 12/9
red= 12
so blue= 9
Question 18.
6 red marbles; 2 for every 5
Answer:
red : blue=2:5
red/blue= 2×3 : 5×3
red= 6
so blue= 15
Question 19.
18 red marbles; 6 to 9
Answer:
red : blue=6:9
red/blue=18/27
red= 18
so blue= 27
Question 20.
12 red marbles; 3 : 4
Answer:
red : blue=3:4
red/blue=12/16
red= 12
so blue= 16
USING A TAPE DIAGRAM A bowl contains blueberries and strawberries. You are given the total number of berries in the bowl and the ratio of blueberries to strawberries. How many of each berry are in the bowl?
Question 21.
16 berries; 3 : 1
Answer:
no of strawberries = 4
no of blueberries = 12
Explanation:
total berries :- 16
ration :- 3:1
no of strawberries :- 1x
no of blueberries :- 3x
3x + 1x = 16
4x = 16
x = 4
Question 22.
10 berries; 2 for every 3
Answer:
no of strawberries :- 3x
no of blueberries :- 2x
2x + 3x = 10
5x = 10
x = 2
no of strawberries :- 3x = 3(2) = 6
no of blueberries :- 2x = 2(2) = 4
Question 23.
12 berries; 1 to 2
Answer:
no of strawberries :- 2x
no of blueberries :- 1x
1x + 2x = 12
3x = 12
x = 4
no of strawberries :- 2x = 2(4) = 8
no of blueberries :- 1x = 1(4) = 4
Question 24.
20 berries; 4 : 1
Answer:
no of strawberries :- 1x
no of blueberries :- 4x
1x + 4x = 20
5x = 20
x = 4
no of strawberries :- 1x = 1(4) = 4
no of blueberries :- 4x = 4(4) = 16
Question 25.
48 berries; 9 to 3
Answer:
no of strawberries :- 3x
no of blueberries :- 9x
3x + 9x = 48
12x = 48
x = 4
no of strawberries :- 3x = 3(4) = 12
no of blueberries :- 9x = 9(4) = 36
Question 26.
46 berries; 11 for every 12
Answer:
no of strawberries :- 12x
no of blueberries :- 11x
12x + 11x = 46
23x = 46
x = 2
no of strawberries :- 12x = 12(2) = 24
no of blueberries :- 11x = 11(2) = 22
Question 27.
PROBLEM SOLVING
You separate bulbs of garlic into two groups: one for planting and one for cooking. The tape diagram represents the ratio of bulbs for planting to bulbs for cooking. You use 6 bulbs for cooking. Each bulb has 8 cloves. How many cloves of garlic will you plant?
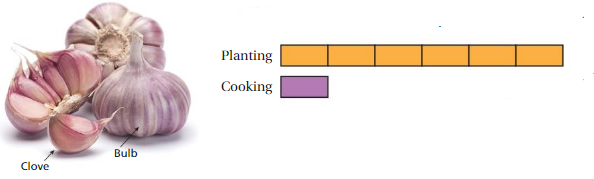
Answer:
Given,
You separate bulbs of garlic into two groups: one for planting and one for cooking.
The tape diagram represents the ratio of bulbs for planting to bulbs for cooking.
You use 6 bulbs for cooking. Each bulb has 8 cloves.
6 : 8
6 × 6 = 36
36 × 8 = 288
Thus you plant 288 cloves of garlic.
Question 28.
MODELING REAL LIFE
Methane gas contains carbon atoms and hydrogen atoms in the ratio of 1 : 4. A sample of methane gas contains 92 hydrogen atoms. How many carbon atoms are in the sample? How many total atoms are in the sample?
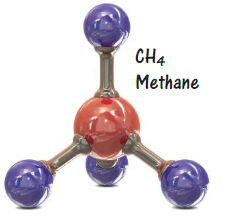
Answer:
Methane: 1 carbon and 4 hydrogens
A sample of methane gas contains 92 hydrogen atoms.
1 : 4 :: x : 92
x = number of carbons
x = 92/4
x = 23 carbons
Total atoms = hydrogen atoms + carbon atoms
= 92 + 23
= 115 atoms
Question 29.
MODELING REAL LIFE
There are 8 more girls than boys in a school play. The ratio of boys to girls is 5 : 7. How many boys and how many girls are in the play?
Answer:
Given,
There are 8 more girls than boys in a school play. The ratio of boys to girls is 5 : 7
5x = 5(4) = 20 boys
7x = 7(4) = 28 girls
To find how many more girls there are than boys in the play,
We have to subtract the number of girls and number of boys
28 – 20 = 8
Thus it means there are 8 more girls than boys in the school play.
Question 30.
DIG DEEPER!
A baseball team sells tickets for two games. The ratio of sold tickets to unsold tickets for the first game was 7 : 3. For the second game, the ratio was 13 : 2. There were 240 unsold tickets for the second game. How many tickets were sold for the first game?
Answer: 1260 tickets were sold on the first game
Explanation:
For the second game, the ratio was 13 : 2.
Total ratio = 13 + 2 = 15
There were 240 unsold tickets for the second game.
Let the total number of tickets for the second game be x.
240 = 2/15 × x
2x = 15 × 240 = 3600
x = 3600/2 = 1800
1800 tickets were sold for the second time.
Assuming total number of tickets for the first game is equal to total number of tickets for the second game.
Therefore total number of tickets sold for the first game is 1800
The ratio of sold tickets to unsold tickets for the first game was 7: 3
Total ratio 7 + 3 = 10
Number of tickets sold for the first game would be 7/10 × 1800 = 12600/10 = 1260 tickets
Question 31.
PROBLEM SOLVING
You have $150 in a savings account and you have some cash. The tape diagram represents the ratio of the amounts of money. You want to have twice the amount of money in your savings account as you have in cash. How much of your cash should you deposit into your savings account?

Answer: $200
Explanation:
We know that:
You have $150 in a savings account.
This is represented with two tiles.
Then each tile represents:
$150/2 = $75
And in cash you have 5 tiles, then in cash you have:
5×$75 = $375.
Then the problem is:
You have $150 in the savings account
You have $375 in cash.
You want to deposit a quantity such that you have twice the amount of money in your savings account as you have in cash.
Suppose that you move a quantity X from cash to the savings account, then now we have the situation:
Sav. Acc. = $150 + X
Cash = $375 – X
And we want that:
Sav. Acc. = 2×Cash
($150 + X) = 2×($375 – X)
Let’s solve this for X.
$150 + X = $750 – 2×X
3×X = $750 – $150 = $600
X = $600/3 = $200
You should deposit $200 in the Savings account.
Question 32.
DIG DEEPER!
A fish tank contains tetras, guppies, and minnows. The ratio of tetras to guppies is 4 : 2. The ratio of minnows to guppies is 1 : 3. There are 60 fish in the tank. How many more tetras are there than minnows? Justify your answer.

Answer: 30
Explanation:
A fish tank contains tetras, guppies, and minnows.
The ratio of tetras to guppies is 4 : 2.
The ratio of minnows to guppies is 1 : 3. There are 60 fish in the tank.
Let number of tetras be t
number of guppies be g
number of minnows be m
Ratio of tetras to guppies is 4:2, or reducing, 2:1
m = g/3
Also, total there are 60 fish
t + g + m = 60
2g + g + g/3 = 60
Now finding t and m:
m = g/3 = 18/3 = 6
m = 6
t = 2g
t = 2(18)
t = 36
There are 36 tetras and 6 minnows. So, there are 36 – 6 = 30 more tetras than minnows
EXPLORATION 1
Making a Table of Equivalent Ratios
Work with a partner. You buy milk that contains 180 calories per 2 cups.
a. You measure 2 cups of the milk for a recipe and pour it into a pitcher. You repeat this four more times. Make a table to show the numbers of calories and cups in the pitcher as you add the milk.
b. Describe any relationships you see in your table.
c. Describe ways that you can find equivalent ratios using different operations.

Answer:
EXPLORATION 2
Creating a Double Number Line
Work with a partner.
a. Represent the ratio in Exploration 1 by labeling the increments on the double number line below. Can you label the increments in more than one way?
b. How can you use the double number line to find the number of calories in 3 cups of milk? 3.5 cups of milk?
Answer:
Lesson 3.3 Using Ratio Tables
You can find and organize equivalent ratios in a ratio table. You can generate a ratio table by using repeated addition or multiplication.

Try It
Find the missing values in the ratio table. Then write the equivalent ratios.
Question 1.
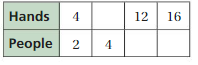
Answer:
Question 2.
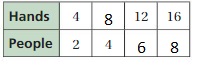
Answer:
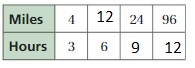
You can also generate a ratio table by using subtraction or division. In summary, you can find equivalent ratios by:
• adding or subtracting quantities in equivalent ratios.
• multiplying or dividing each quantity in a ratio by the same number.
Try It
Find the missing values in the ratio table. Then write the equivalent ratios.
Question 3.
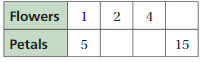
Answer:
2:10 = 1:5
4:20 = 1:5
3:15 = 1:5
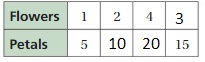
Question 4.
Answer:
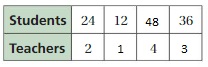
The ratio is 12:1
The equivalent ratios are
24:2 = 12:1
48:4 = 12:1
36:3 = 12:1
Question 5.
WHAT IF?
You eat 21 crackers. How much sodium do you consume?
Answer:
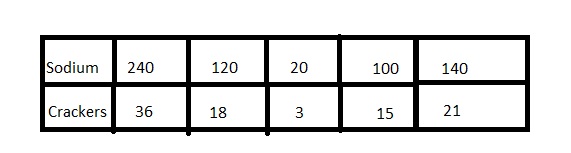
Add the middle two columns
120 + 20 = 140
18 + 3 = 21 crackers
Thus you consume 140 mg sodium.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
COMPLETING A RATIO TABLE Find the missing values in the ratio table. Then write the equivalent ratios.
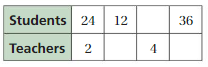
Question 6.
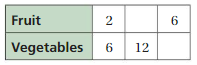
Answer:
The missing values in the ratio are 4, 12, 18
The ratio is 2:6
The equivalent ratio of 2:6 are 4:12, 6:18
Question 7.
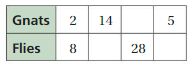
Answer:
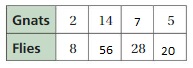
The missing values in the ratio are 56, 7, 20
The ratio is 2:8
The equivalent ratio of 2:8 are 14:56, 7:28, 5:20
Question 8.
WRITING
Explain how creating a ratio table using repeated addition is similar to creating a ratio table using multiplication.
Answer:
Ratio tables are constructed in a special way. Each pair of values in the table will be equivalent to the same ratio. You can use repeated addition or multiplication to create a ratio table. There is a constant value that we can multiply the values in the first column by to get the values in the second column.
Question 9.
You mix 7 tablespoons of vinegar for every 4 tablespoons of baking soda to produce a chemical reaction. You use 15 tablespoons of baking soda. How much vinegar do you use?
Answer:
Given,
You mix 7 tablespoons of vinegar for every 4 tablespoons of baking soda to produce a chemical reaction.
You use 15 tablespoons of baking soda.
Case 1:
Tablespoon of vinegar taken = 7
Tablespoon of baking soda taken = 4
The ratio between v and b = 7:4
Case 2:
Tablespoon of vinegar taken = x
Tablespoon of baking soda taken = 15
The ratio between v and b = x:15
7:4 : : x:15
7 × 15 = 4 × x
4x = 105
x = 105/4
x = 26.25
Thus you use 26.25 teaspoons.
Question 10.
You make a carbonated beverage by adding 7 ounces of soda water for every 3 ounces of regular water. Your friend uses 11 ounces of soda water for every 4 ounces of regular water. Whose beverage is more carbonated?

Answer:
The proportion of soda in the drink will show us how carbonated a beverage is. The proportion of soda is the ounce of soda divided by the sum of the soda and water.
The proportion of soda in the first beverage
7/(7+3) = 7/10 = 0.7
The proportion of soda in the first beverage
11/(11+4) = 11/15 = 0.73
Therefore the second beverage is more carbonated.
Using Ratio Tables Homework & Practice 3.3
Review & Refresh
A bag contains green tokens and black tokens. You are given the number of green tokens in the bag and the ratio of green tokens to black tokens. Find the number of black tokens in the bag.
Question 1.
green tokens; 4 for every 1
Answer:
no of green tokens:- 4x
no of black tokens:- 1x
x = 1
no of green tokens:- 4x = 4(1) = 4
no of black tokens:- 1x = 1() = 1
Question 2.
6 green tokens; 2 : 7
Answer:
no of green tokens:- 2x
no of black tokens:- 7x
2x + 7x = 6
9x = 6
x = 6/9
x = 2/3
no of green tokens:- 2x = 2(2/3) = 4/3
no of black tokens:- 7x = 7(2/3) = 14/3
Question 3.
24 green tokens; 8 to 5
Answer:
no of green tokens:- 8x
no of black tokens:- 5x
8x + 5x = 24
13x = 24
x = 24/13
no of green tokens:- 8x = 8(24/13) = 14.7
no of black tokens:- 5x = 5(24/13) = 9.23
Question 4.
36 green tokens; 3 for every 4
Answer:
no of green tokens:- 3x
no of black tokens:- 4x
3x + 4x = 36
7x = 36
x = 36/7
no of green tokens:- 3x = 3(36/7) = 15.42
no of black tokens:- 4x = 4(36/7) = 20.57
Find the GCF of the numbers.
Question 5.
8, 16
Answer: 8
Explanation:
The factors of 8 are: 1, 2, 4, 8
The factors of 16 are: 1, 2, 4, 8, 16
Then the greatest common factor is 8.
Question 6.
48, 80
Answer: 16
Explanation:
The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
The factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Then the greatest common factor is 16.
Question 7.
15, 45, 100
Answer: 5
Explanation:
The factors of 15 are: 1, 3, 5, 15
The factors of 45 are: 1, 3, 5, 9, 15, 45
The factors of 100 are: 1, 2, 4, 5, 10, 20, 25, 50, 100
Then the greatest common factor is 5.
Evaluate the expression.
Question 8.
35 – 2 × 42
Answer:
35 – 2 × 42
35 – 2 × 16
35 – 32 = 3
Question 9.
12 ÷ (1 + 33 – 24)
Answer:
12 ÷ (1 + 33 – 24)
12 ÷ (1 + 27 – 16)
12 ÷ (28 – 16)
12 ÷ 12 = 1
Question 10.
82 ÷ [(11 – 3) . 2]
Answer:
82 ÷ [(11 – 3) . 2]
82 ÷ [8 . 2]
82 ÷ 16
64 ÷ 16 = 4
Find the perimeter of the rectangle.
Question 11.
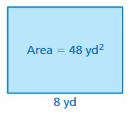
Answer:
Given Area = 48 sq. yd
Length = 8 yd
Width = x
Area of the rectangle = l × w
48 = 8 × x
x = 48/8 = 6
x = 6 yd
Thus the width of the rectangle = 6 yd
Perimeter of the rectangle = 2l + 2w
P = 2(8) + 2(6)
P = 16 + 12
P = 28
Thus the perimeter of the rectangle = 28 yards
Question 12.
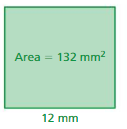
Answer:
Given Area = 132 sq. mm
Length = 12 mm
Width = x
Area of the rectangle = l × w
132 = 12 × x
x = 132/12 = 11
x = 11 mm
Thus the width of the rectangle = 11 mm
Perimeter of the rectangle = 2l + 2w
P = 2(12) + 2(11)
P = 24 + 22
P = 46
Thus the perimeter of the rectangle = 46 mm
Concepts, Skills, & Problem Solving
USING A RATIO TABLE Use a ratio table to find the number of calories in the indicated number of cups of milk from Exploration 1. Explain your method. (See Exploration 1, p. 121.)
Question 13.
16 cups
Answer:
You buy milk that contains 180 calories per 2 cups.
1 cup = 180/2 = 90 calories
16 cups = 16 × 90 = 1440 calories
Question 14.
18 cups
Answer:
You buy milk that contains 180 calories per 2 cups.
1 cup = 180/2 = 90 calories
18 cups = 18 × 90 = 1620 calories
Question 15.
5.5 cups
Answer:
You buy milk that contains 180 calories per 2 cups.
1 cup = 180/2 = 90 calories
5.5 cups = 5.5 × 90 = 495 calories
COMPLETING RATIO TABLES Find the missing value(s) in the ratio table. Then write the equivalent ratios.
Question 16.
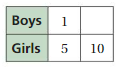
Answer:
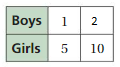
The ratio is 1 : 5
The equivalent ratio with 10 is 2 : 10
Question 17.
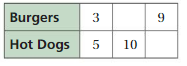
Answer:
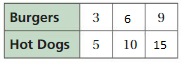
The ratio is 3 : 5
The equivalent ratio is 6 : 10, 9 : 15
Question 18.
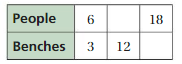
Answer:
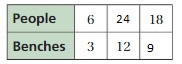
The ratio is 6 : 3
The equivalent ratio is 24 : 12, 18 : 9
Question 19.
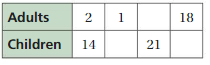
Answer:
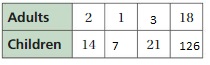
The ratio is 2 : 14
The equivalent ratio is 1 : 7, 3 : 21, 18 : 126
Question 20.
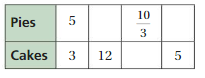
Answer:
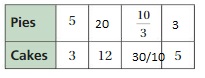
Question 21.
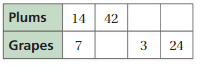
Answer:
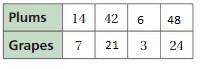
Question 22.
YOU BE THE TEACHER
Your friend creates a ratio table for the ratio 5 : 3. Is your friend correct? Explain your reasoning.
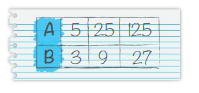
Answer: No your friend is incorrect. Because 125 : 27 is not the equivalent ratio of 5 : 3
COMPLETING RATIO TABLES Complete the ratio table to solve the problem.
Question 23.
For every 3 tickets you sell, your friend sells 4 tickets. You sell a total of 12 tickets. How many tickets does your friend sell?
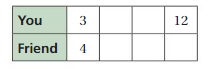
Answer:
The ratio is 3 : 4
So divide 12 by 3 = 4 and sells 16 tickets
Thus the ratio is 12 : 16 = 3 : 4
Question 24.
A store sells 2 printers for every 5 computers. The store sells 40 computers. How many printers does the store sell?
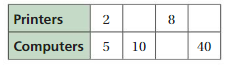
Answer:
Let us think of 2 printers for every 5 computers as a set.
First let us determine hoe many sets were sold to get to 40 computers
5x = 40
x = 8
2x = 2(8) = 16
This means 16 printers were sold.
Question 25.
First and second place in a contest use a ratio to share a cash prize. When first place pays $100, second place pays $60. How much does first place pay when second place pays $36?
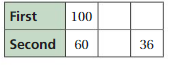
Answer: $60
Explanation:
Given,
First and second place in a contest use a ratio to share a cash prize. When first place pays $100, second place pays $60.
Let x be the pay of the first place when the second place pays $36
100/60 = x/36
x = $60
Question 26.
A grade has 81 girls and 72 boys. The grade is split into groups that have the same ratio of girls to boys as the whole grade. How many girls are in a group that has 16 boys?
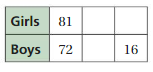
Answer:
A grade has 81 girls and 72 boys. The grade is split into groups that have the same ratio of girls to boys as the whole grade.
We have to find how many girls are in a group that has 16 boys
81 : 72 = x : 16
16 × 81 = 1296
1296/72 = 18
Therefore the value of girls numbers is 18.
The new ratio will be 18 : 16
USING A DOUBLE NUMBER LINE Find the missing quantity in the double number line.
Question 27.
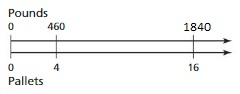
Answer:
The equivalent ratio of 460 : 4 is 1840 : 16
Question 28.
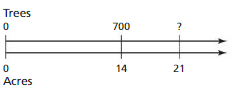
Answer:
The equivalent ratio of 700 : 14 is 1050 : 21
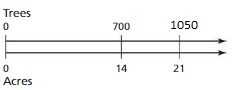
Question 29.
PROBLEM SOLVING
A company sets sales goals for employees each month.
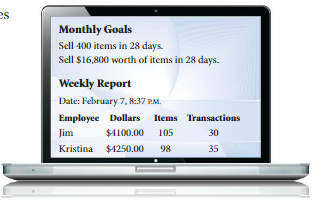
a. At her current pace, how many items will Kristina sell in 28 days? Is she on track to meet the goal? Explain.
b. At his current pace, how many dollars worth of product will Jim sell in 28 days? Is he on track to meet the goal? Explain.
Answer:
Question 30.
MODELING REAL LIFE
A gold alloy contains 15 milligrams of gold for every 4 milligrams of copper. A jeweler uses 48 milligrams of copper to make the alloy. How much gold does the jeweler use to make the alloy?

Answer:
There are 180 milligrams of gold in the alloy.
Explanation:
We know that for every 4 milligrams of copper, there are 15 milligrams of gold.
if 48 milligrams of copper are used, we can separate them in “sets” of 4 milligrams.
We have 48/4 = 12 sets.
And for each one of these 12 sets, there are 15 milligrams of gold, then the total amount of gold in the alloy is:
12×15mg = 180 mg
Question 31.
MODELING REAL LIFE
You make candles by adding 2 fluid ounces of scented oil for every 22 fluid ounces of wax. Your friend makes candles by adding 3 fluid ounces of the same scented oil for every 37 fluid ounces of wax. Whose candles are more fragrant? Explain your reasoning.
Answer: Your candles are more fragrant
Explanation:
Given,
You make candles by adding 2 fluid ounces of scented oil for every 22 fluid ounces of wax.
Your friend makes candles by adding 3 fluid ounces of the same scented oil for every 37 fluid ounces of wax.
Compare 2/22 and 3/37
2/22 > 3/37
By this we can say that your candles are more fragrant.
Question 32.
MODELING REAL LIFE
A mint milk shake contains 1.25 fluid ounces of milk for every 4 ounces of ice cream. A strawberry milk shake contains 1.75 fluid ounces of milk for every 5 ounces of ice cream. Which milk shake is thicker? Explain.
Answer:
CRITICAL THINKING Two whole numbers A and B satisfy the following conditions. Find A and B.
Question 33.
A + B = 30
A : B is equivalent to 2 : 3.
Answer:
Let A = 2x
Let B = 3x
2x + 3x = 30
5x = 30
x = 30/5 = 6
x = 6
A = 2x = 2(6) = 12
B = 3(6) = 18
A : B = 12 : 18
Question 34.
A + B = 44
A : B is equivalent to 4 : 7.
Answer:
Let A = 4x
Let B = 7x
4x + 7x = 44
11x = 44
x = 44/11
x = 4
A = 4x = 4(4) = 16
B = 7x = 7(4) = 28
A : B = 16 : 28
Question 35.
A – B = 18
A : B is equivalent to 11 : 5.
Answer:
Let A = 11x
Let B = 5x
11x – 5x = 18
6x = 18
x = 18/6
x = 3
A = 11x = 11(3) = 33
B = 5x = 5(3) = 15
33 – 15 = 18
A : B = 33 : 15
Question 36.
A – B = 25
A : B is equivalent to 13 : 8.
Answer:
Let A = 13x
Let B = 8x
13x – 8x = 25
5x = 25
x = 5
A = 13x = 13(5) = 65
B = 8(5) = 40
A : B = 65 : 40
Question 37.
MODELING REAL LIFE
A nutrition label shows that there are 161 calories in 28 grams of dry roasted cashews. You eat 9 cashews totaling 12 grams.

a. Do you think it is possible to find the number of calories you consume? Explain your reasoning.
Answer:
There are 161 calories in 28 grams. You eat 9 cashews totaling 12 grams.
We need to find out how many calories in 12 grams
For that we make a proportion
Calories/grams = calories/grams
161/28 = x/12
28x = 161 × 12
x = 1932/28
x = 69
There are 69 calories in 12 grams
b. How many cashews are in one serving?
Answer:
Divide 161 by 28 to get the calorie count for one gram
Multiply that by 12 to work out how many calories you have eaten in the 9 cashews 161/28 = 5.75
5.75 x 12 = 69
Question 38.
REASONING
The ratio of three numbers is 4 : 5 : 3. The sum of the numbers is 54. What are the three numbers?
Answer:
Let it be x.
4x + 5x + 3x = 54
12x = 54
x = 54/12
x = 4.5
Now 4x = 4× 4.5 = 18
3x = 3 × 4.5
=13.5
5x = 5× 4.5 = 22.5
Question 39.
CRITICAL THINKING
Seven out of every 8 students surveyed own a bike. The difference between the number of students who own a bike and those who do not is 72. How many students were surveyed?
Answer:
So if x people were surveyed, 7/8 people owned a bike and 1/8 did not.
The difference between them is 72
7/8 × x – 1/8 = 72
So, this means that,
6/8 x = 72
Let us simpify
3/4 × x = 72
1/4 × x = 24
and multiply by 4
x = 96
So 96 people were surveyed
Question 40.
LOGIC
You and a classmate have a bug collection for science class. You find 5 out of every 9 bugs in the collection. You find 4 more bugs than your classmate. How many bugs are in the collection?

Answer:
Let b represent the total amount bugs.
5/9 × b = 4/9 × b + 4
1/9 × b = 4
b = 4 × 9
b = 36
There are 36 bugs in the collection.
Question 41.
PROBLEM SOLVING
You earn $72 for every 8 hours you spend shoveling snow. You earn $60 for every 5 hours you spend babysitting. For every 3 hours you spend babysitting, you spend 2 hours shoveling snow. You babysit for 15 hours in January. How much money do you earn in January?
Answer: $90
Explanation:
Earning for 8 hours shoveling snow = $72
Amount per hour = $72/8 = $9
3 hours of babysitting = 2 hours shoveling snow
Babysitting hours in January = 15 hours
Hours of shoveling snow in January = (15/3) x 2 = 10 hours
Amount earned in January = Hours shoveling snow x Hourly Rate
= 10 x $9 = $90
That is, you earn $90 in January.
Question 42.
DIG DEEPER!
You and a friend each have a collection of tokens. Initially, for every 8 tokens you had, your friend had 3. After you give half of your tokens to your friend, your friend now has 18 more tokens than you. Initially, how many more tokens did you have than your friend?
Answer: 30 token
Explanation:
Initially, for every 8 tokens I had, my friend had 3.
Therefore, ratio of tokens that me and my friend is 8 : 3
Let I have 8 x tokens and my friend has 3 x tokens, where x is any number.
Then again according to the question,
After I gave half of your friend, my friend now has 18 more tokens than you.
That is, (3x + 4x) – 4x = 18
7x – 4x = 18
3x = 18
x = 6
Therefore , Initially the difference between me and my friend’s token = 8 x – 3 x = 5 x = 5 × 6 = 30
Lesson 3.4 Graphing Ratio Relationships
EXPLORATION 1
Using a Coordinate Plane
Work with a partner. An airplane travels 300 miles per hour.
a. Represent the relationship between distance and time in a coordinate plane. Explain your choice for labeling and scaling the axes.
b. Write a question that can be answered using the graph. Exchange your question with another group. Answer their question and discuss the solution with the other group.

Answer:
EXPLORATION 2
Identifying Relationships in Graphs
Work with a partner. Use the graphs to make a ratio table. Explain how the blue, red, and green arrows correspond to the ratio table.
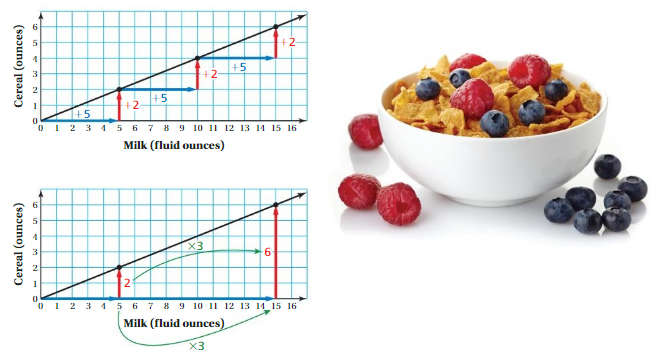
Answer:
For a ratio of two quantities, you can use equivalent ratios to create ordered pairs of the form (first quantity, second quantity). You can plot these ordered pairs in a coordinate plane and draw a line, starting at(0, 0), through the points.
Try It
Represent the ratio relationship using a graph.
Question 1.
Answer:
Question 2.
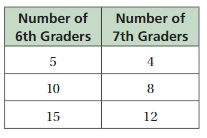
Answer:
Question 3.
WHAT IF?
Repeat Example 2 when the cost of the dark chocolate cashews is $15 per pound.
Answer:
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 4.
GRAPHING A RATIO RELATIONSHIP
Represent the ratio relationship using a graph.
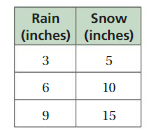
Answer:
Question 5.
CRITICAL THINKING
Use what you know about equivalent ratios to explain why the graph of a ratio relationship passes through (0, 0).
Answer:
Question 6.
WHICH ONE DOESN’T BELONG?
Which ordered pair does not belong with the other three? Explain your reasoning.
Answer: (24, 4) does not belong with the other three.
(4, 1) (8, 2) (12, 3) are the equivalent ordered pairs.
Question 7.
You are skateboarding at a pace of 30 meters every 5 seconds. Your friend is in-line skating at a pace of 9 meters every 2 seconds. Graph each ratio relationship in the same coordinate plane. Who is faster?

Answer:
Question 8.
You buy 2.5 pounds of pumpkin seeds and 2.5 pounds of sunflower seeds. Use a graph to find your total cost. Then use the graph to determine how much more you pay for pumpkin seeds than for sunflower seeds.

Answer:
Graphing Ratio Relationships Homework & Practice 3.4
Review & Refresh
Find the missing values in the ratio table. Then write the equivalent ratios.
Question 1.
Answer:
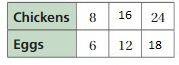
The pattern of chickens is multiple of 8.
So, the missing values in the ratio table is 16.
The pattern of Eggs is multiple of 6.
So, the missing values in the ratio table is 18.
Question 2.
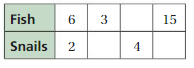
Answer:
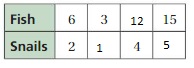
The missing values are 1, 12, 5
The equivalent ratios are 3 : 1, 12:4, 15:5
Write the name of the decimal number.
Question 3.
7.1
Answer:
We start by naming the number to the left of the decimal. We use the word “and” to indicate the decimal point. Then we name the number to the right of the decimal point as if it were a whole number.
7.1 can be written as seven and one.
Question 4.
3.54
Answer:
We start by naming the number to the left of the decimal. We use the word “and” to indicate the decimal point. Then we name the number to the right of the decimal point as if it were a whole number.
3.54 can be written as three and five four
Question 5.
13.6
Answer:
We start by naming the number to the left of the decimal. We use the word “and” to indicate the decimal point. Then we name the number to the right of the decimal point as if it were a whole number.
13.6 can be written as thirteen and six
Question 6.
8.132
Answer:
We start by naming the number to the left of the decimal. We use the word “and” to indicate the decimal point. Then we name the number to the right of the decimal point as if it were a whole number.
8.132 can be written as eight and one thirty two
Write two equivalent ratios that describe the relationship.
Question 7.
baseballs to gloves

Answer: The ratio from baseballs to gloves is 8: 4
The equivalent ratios are 2 : 1, 16 : 8
Question 8.
ladybugs to bees

Answer: The ratio from ladybugs to bees is 12 : 4
The equivalent ratios are 3 : 1 and 24 : 8
Concepts, Skills, & Problem Solving
USING A COORDINATE PLANE Represent the relationship between distance and time in a coordinate plane. (See Exploration 1, p. 129.)
Question 9.
A train travels 45 miles per hour.
Answer:
Question 10.
A motorcycle travels 70 kilometers per hour.
Answer:
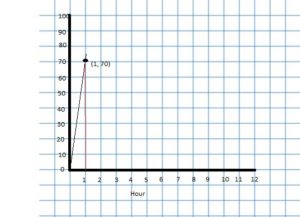
Question 11
A snail travels 80 centimeters per minute.
Answer:
Question 12.
A whale travels 800 yards per minute.
Answer:
GRAPHING RATIO RELATIONSHIPS Represent the ratio relationship using a graph.
Question 13.
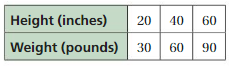
Answer:
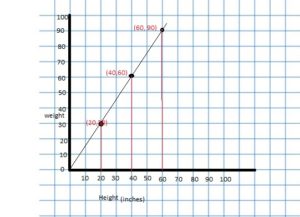
Question 14.
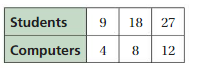
Answer:
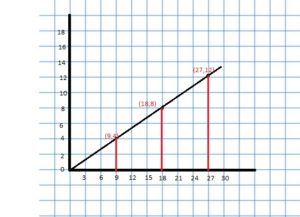
Question 15.
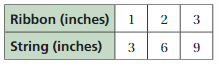
Answer:
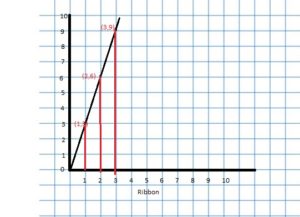
Question 16.
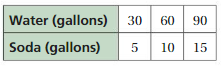
Answer:
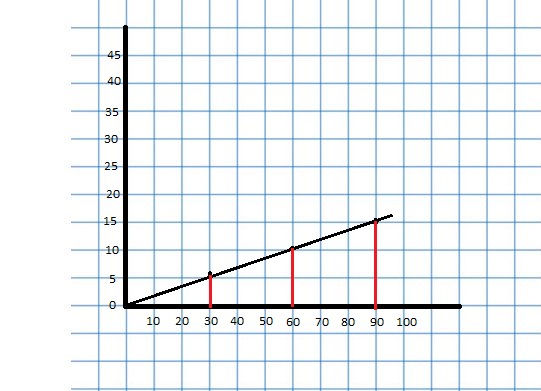
Question 17.
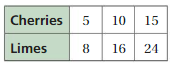
Answer:
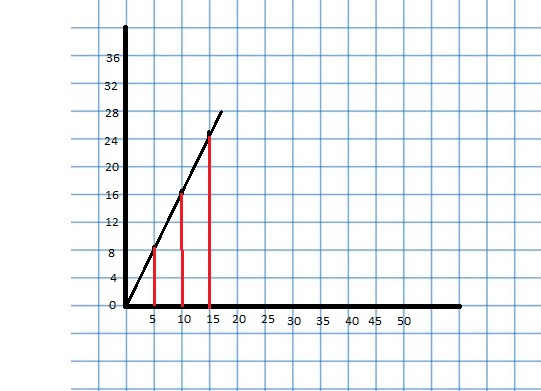
Question 18.
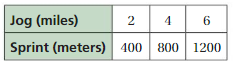
Answer:
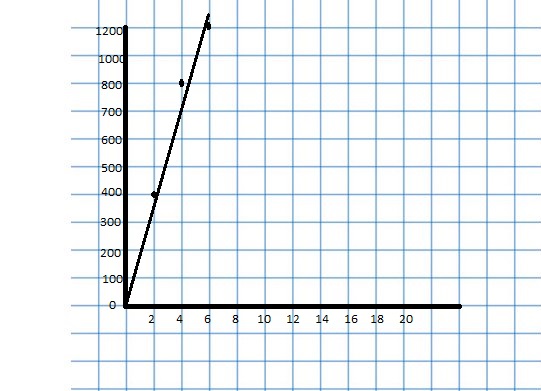
Question 19.
MODELING REAL LIFE
A radio station collects donations for a new broadcast tower. The cost to construct the tower is $25.50 per inch.
a. Represent the ratio relationship using a graph.
b. How much does it cost to fund 4.5 inches of the construction?
Answer:
Question 20.
MODELING REAL LIFE
Your school organizes a clothing drive as a fundraiser for a class trip. The school earns $100 for every 400 pounds of donated clothing.
a. Represent the ratio relationship using a graph.
b. How much money does your school earn for donating 2200 pounds of clothing?
Answer:
Question 21.
NUMBER SENSE
Just by looking at the graph, determine who earns a greater hourly wage. Explain.
Answer: By seeing the above graph we can say that you earns greater hourly wage.
Question 22.
MODELING REAL LIFE
An airplane traveling from Chicago to Los Angeles travels 15 miles every 2 minutes. On the return trip, the plane travels 25 miles every 3 minutes. Graph each ratio relationship in the same coordinate plane. Does the plane fly faster when traveling to Los Angeles or to Chicago?
Answer:
Question 23.
MODELING REAL LIFE
Your freezer produces 8 ice cubes every 2 hours. Your friend’s freezer produces 24 ice cubes every 5 hours. Graph each ratio relationship in the same coordinate plane. Whose freezer produces ice faster?
Answer:
Question 24.
CHOOSE TOOLS
A chemist prepares two acid solutions.

a. Use a ratio table to determine which solution is more acidic.
b. Use a graph to determine which solution is more acidic.
c. Which method do you prefer? Explain.
Answer:
Question 25.
DIG DEEPER!
A company offers a nut mixture with 7 peanuts for every 3 almonds. The company changes the mixture to have 9 peanuts for every 5 almonds, but the number of nuts per container does not change.

a. How many nuts are in the smallest possible container?
b. Graph each ratio relationship. What can you conclude?
c. Almonds cost more than peanuts. Should the company change the price of the mixture? Explain your reasoning.
Answer:
Question 26.
STRUCTURE
The point (p, q) is on the graph of values from a ratio table. What are two additional points on the graph?
Answer:
Lesson 3.5 Rates and Unit Rates
EXPLORATION 1
Using a Diagram
Work with a partner. The diagram shows a story problem.
a. What information can you obtain from the diagram?
b. Assuming that the car travels at a constant speed, how far does the car travel in 3.25 hours? Explain your method.
c. Draw a speedometer that shows the speed of the car. How can you use the speedometer to answer part(b)?
Answer:
EXPLORATION 2
Using Equivalent Ratios
Work with a partner. Count the number of times you can clap your hands in 12 seconds. Have your partner record your results. Then switch roles with your partner and repeat the process.
a. Using your results and your partner’s results, write ratios that represent the numbers of claps for every 12 seconds.
b. Explain how you can use the ratios in part(a) to find the numbers of times you and your partner can clap your hands in 2 minutes, in 2.5 minutes, and in 3 minutes.

Answer:
A rate is a ratio of two quantities using different units. You solved various ratio problems in the previous sections that involved rates. Now you will use unit rates to solve rate problems.

Try It
Question 1.
WHAT IF?
Repeat Example 1 when you add 4 pints of water for every 3 cups of concentrate.
Answer:
Question 2.
WHAT IF?
Repeat Example 2 when the space junk travels 3 miles every 5 seconds.
Answer:
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FINDING UNIT RATES Write a unit rate for the situation.
Question 3.
revolutions in 50 seconds
Answer:
Question 4.
1400 words for every 4 pages
Answer:
1400 – 4 pages
x – 1 page
4 × x = 1400
x = 1400/4
x = 350
Thus 350 words for every 1 page.
Question 5.
WHICH ONE DOESN’T BELONG?
Which rate does not belong with the other three? Explain your reasoning.

Answer: 20 pounds per 4 feet does not belong with the other three.
Explanation:
8 pounds for every 2 feet
8/2 = 4 feet
12 pounds per 3 feet
12/3 = 4 feet
20 pounds per 4 feet
20/4 = 5 feet
24 pounds for every 6 feet
24/6 = 4 feet
Question 6.
You buy 10 pounds of birdseed at Store A for $11.50. Your friend buys 15 pounds of birdseed at Store B for $19.50. How much less would you spend by buying 20 pounds of birdseed at the store with the better deal?
Answer: Store A
Explanation:
Given,
You buy 10 pounds of birdseed at Store A for $11.50.
10 pounds – $11.50
1 pound – $1.15
20 pounds = 20 × 1.15 = $23
Your friend buys 15 pounds of birdseed at Store B for $19.50.
15 pounds – $19.50
1 pound – $1.3
1.3 × 20 = $26
$23 < $26
Question 7.
A person hikes 4 miles in 2.5 hours. Find the unit rate in miles per hour. Then find the unit rate in hours per mile. How is each unit rate useful in a real-life situation?
Answer: 1.6 kilometer per hour
Explanation:
The unit rate is the number of miles in 1 hour.
Given,
Distance = 4 miles
Time = 2.5 hours
So if he hike 4 miles in 2.5 hours
then he will hike x mile in 1 hour
x = 4/2.5
x = 1.6 miles per hour
Question 8.
DIG DEEPER!
You buy 11 bagels with a $20 bill. How much change do you receive? How many more bagels could you buy?

Answer:
Rates and Unit Rates Homework & Practice 3.5
Review & Refresh
Represent the ratio relationship using a graph.
Question 1.
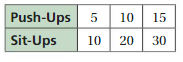
Answer:
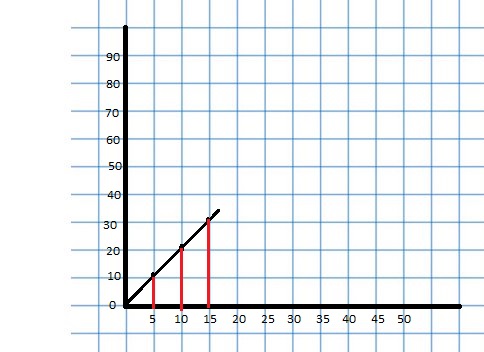
Question 2.
Answer:
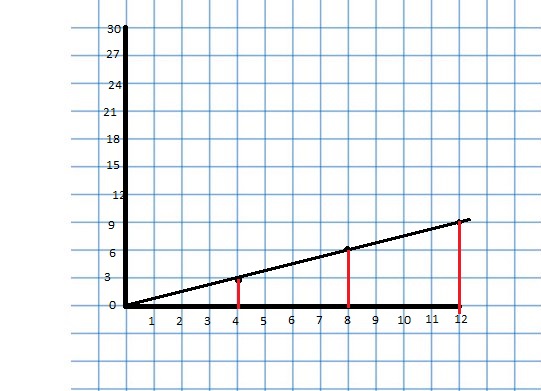
Question 3.
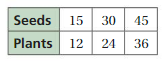
Answer:
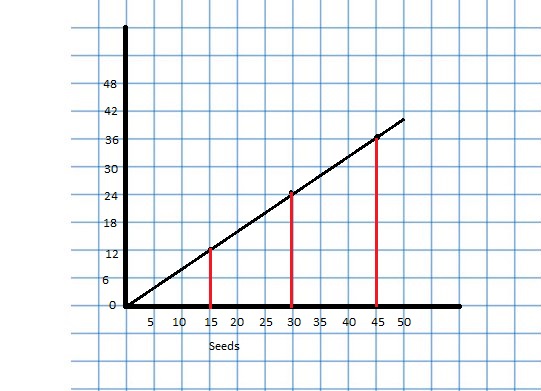
Question 4.
Answer:
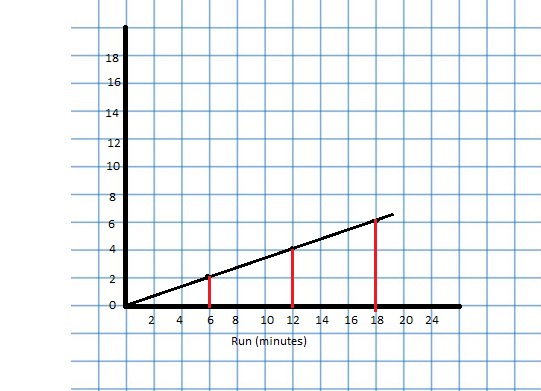
Divide. Write the answer in simplest form.
Question 5.
\(\frac{1}{5}\) ÷ \(\frac{3}{10}\)
Answer: \(\frac{2}{3}\)
Explanation:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes
\(\frac{1}{5}\) × \(\frac{10}{3}\) = \(\frac{10}{15}\) = \(\frac{2}{3}\)
Question 6.
\(\frac{3}{8}\) ÷ 6
Answer: \(\frac{1}{16}\)
Explanation:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes
\(\frac{3}{8}\) × \(\frac{1}{6}\) = \(\frac{1}{16}\)
Question 7.
3\(\frac{1}{6}\) ÷ 2
Answer: 1 \(\frac{7}{12}\)
Explanation:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes
3\(\frac{1}{6}\) = \(\frac{19}{6}\)
\(\frac{19}{6}\) × \(\frac{1}{2}\) = 1 \(\frac{7}{12}\)
Question 8.
5\(\frac{1}{3}\) ÷ 2\(\frac{2}{3}\)
Answer: 2
Explanation:
Convert any mixed numbers to fractions.
5\(\frac{1}{3}\) = \(\frac{16}{3}\)
2\(\frac{2}{3}\) = \(\frac{8}{3}\)
\(\frac{16}{3}\) × \(\frac{3}{8}\) = \(\frac{48}{24}\) = 2
Add or subtract.
Question 9.
6.94 + 12.301
Answer: 19.241
Question 10.
8.753 – 7.71
Answer: 1.043
Question 11.
14.532 – 6.613
Answer: 7.919
Question 12.
The winner in an election for class president received \(\frac{3}{4}\) of the 240 votes. How many votes did the winner receive?
A. 60
B. 150
C. 180
D. 320
Answer: 180
Explanation:
Given,
The winner in an election for class president received \(\frac{3}{4}\) of the 240 votes.
\(\frac{3}{4}\) × 240 = 180
The winner receive 180 votes.
Thus the correct answer is option C
Concepts, Skills, & Problem Solving
USING EQUIVALENT RATIOS Use the ratio in Exploration 2 to estimate the number of times you can clap your hands in the given amount of time. (See Exploration 2, p. 135.)
Question 13.
0.5 minute
Answer:
Question 14.
1.75 minutes
Answer:
Question 15.
2.25 minutes
Answer:
FINDING UNIT RATES Write a unit rate for the situation.
Question 16.
24 animals in 2 square miles
Answer: 12 animals
Explanation:
Given,
24 animals in 2 square miles
24/2 = 12
12 animals in 1 square mile
Question 17.
$100 for every 5 guests
Answer: $20
Explanation:
Given,
$100 for every 5 guests
100/5 = $20
$20 per guest.
Question 18.
$28 saved in 4 weeks
Answer: $7
Explanation:
Given,
$28 saved in 4 weeks
28/4 = $7
$7 per week
Question 19.
18 necklaces made in 3 hours
Answer: 6 necklaces
Explanation:
Given,
18 necklaces made in 3 hours
18/3 = 6
6 necklaces made in 1 hour
Question 20.
270 miles in 6 hours
Answer: 45 miles per hour
Explanation:
Given,
270 miles in 6 hours
270/6 = 45
45 miles in 1 hour
Question 21.
228 students in 12 classes
Answer: 24 students per class
Explanation:
Given,
228 students in 12 classes
228/12 = 24
24 students in 1 class
Question 22.
2520 kilobytes in 18 seconds
Answer: 140 kilobytes per second
Explanation:
Given,
2520 kilobytes in 18 seconds
2520/18 = 140 kilobytes
140 kilobytes per second
Question 23.
880 calories in 8 servings
Answer: 110 calories in 1 serving
Explanation:
Given,
880 calories in 8 servings
880/8 = 110
110 calories in 1 serving
Question 24.
1080 miles on 15 gallons
Answer: 72 miles in 1 gallon
Explanation:
Given,
1080 miles on 15 gallons
1080/15 = 72 miles
72 miles in 1 gallon
Question 25.
$12.50 for 5 ounces
Answer: 2.5
Explanation:
Given,
$12.50 for 5 ounces
12.50/5 = 2.5
$2.5 per ounce
USING UNIT RATES Find the missing values in the ratio table.
Question 26.
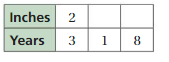
Answer:
Question 27.
Answer:
Question 28.
MODELING REAL LIFE
Lightning strikes Earth 1000 times in 10 seconds.

a. How many times does lightning strike in 12 seconds?
b. How many seconds does it take for lightning to strike 7250 times?
Answer:
Question 29.
MODELING REAL LIFE
You earn $35 for washing 7 cars.
a. How much do you earn for washing 4 cars?
Answer:
Given,
You earn $35 for washing 7 cars.
7 cars = $35
1 car = x
x × 7 = $35
x = 35/7 = 5
Thus you earn $5 per car
4 cars = 4 × 5 = $20
You earn $20 for washing 4 cars..
b. You earn $45. How many cars did you wash?
Answer:
you earn $5 per car
45/5 = 9
You wash 9 cars for $45
COMPARING RATES Decide whether the rates are equivalent.
Question 30.
24 laps in 6 minutes
72 laps in 18 minutes
Answer: Yes
Explanation:
24:6 = 4 : 1
72 : 18 = 4 : 1
Thus the rates are equivalent.
Question 31.
126 points for every 3 games
210 points for every 5 games
Answer: Yes
Explanation:
Given
126 points for every 3 games
210 points for every 5 games
126 : 3 = 42 : 1
210 : 5 = 42 : 1
Thus the rates are equivalent.
Question 32.
15 breaths for every 36 seconds
90 breaths for every 3 minutes
Answer: No
Explanation:
Given
15 breaths for every 36 seconds
90 breaths for every 3 minutes
15 : 36 = 0.41
90 : 180 = 0.5
Thus the rates are not equivalent.
Question 33.
$16 for 4 pounds
$1 for 4 ounces
Answer: Yes
Explanation:
Given
$16 for 4 pounds
$1 for 4 ounces
1 pound = 16 ounces
4 pounds = 64 ounces
16 : 64 = 1 : 4
Thus the rates are equivalent.
Question 34.
MODELING REAL LIFE
An office printer prints 25 photos in 12.5 minutes. A home printer prints 15 photos in 6 minutes. Which printer is faster? How many more photos can you print in 12 minutes using the faster printer?
Answer: The home printer is faster
Explanation:
Given,
An office printer prints 25 photos in 12.5 minutes. A home printer prints 15 photos in 6 minutes.
23 photos in 12.5 minutes
12.5 is half of 25 and therefore this is a two to one ratio
So 2 photos print in 1 minute with the office printer.
And 4 photos in 2 minutes.
The home printer prints 15 photos in 6 minutes.
Since 15 is not divisible by 6 without a remainder divide both by 3.
So 5 photos in 2 minutes. This is faster than the office printer.
This leaves you with an answer of 30 photos in 12 minutes.
Question 35.
MODELING REAL LIFE
You jog 2 kilometers in 12 minutes. Your friend jogs 3 kilometers in 16.5 minutes. Who jogs faster? How much sooner will the faster jogger finish a five-kilometer race?
Answer:
First, we have to calculate the speed of person 1 and 2.
Speed = Distance/time
Speed of person 1 = 2/12 = 0.167 km/min
Speed of person 2 = 3/16.5 = 0.182 km/min
From this we conclude that, person 2 jogs faster as compared to person 1.
Now we have to calculate the time taken by the faster jogger to finish a 5 kilometer race.
Faster jogger speed = 0.182 km/min
Distance = 5 km
S = d/t
Time = 27.5 min
Thus, the time taken by the faster jogger finish a 5 kilometer race will be, 27.5 minutes.
Question 36.
PROBLEM SOLVING
A softball team has a budget of $200 for visors. The athletic director pays $90 for 12 sun visors. Is there enough money in the budget to purchase 15 more sun visors? Explain your reasoning.
Answer: $112.5
Explanation:
An athletic director pays $90 for 12 sun visors for the softball team.
The rate per sun visor is equal to $90/12 = $7.5
So the athletic director should pay
$7.5 × 15 = $112.5
Question 37.
DIG DEEPER!
The table shows the amounts of food collected by two homerooms. Homeroom A collects 21 additional items of food. How many more items does Homeroom B need to collect to have more items per student?
Answer:
Question 38.
REASONING
A runner completed a 26.2-mile marathon in 210 minutes.
a. Estimate the unit rate, in miles per minute.
b. Estimate the unit rate, in minutes per mile.
c. Another runner says, “I averaged 10-minute miles in the marathon.” Is this runner talking about the unit rate described in part(a) or in part(b)? Explain your reasoning.

Answer:
Question 39.
DIG DEEPER!
You can complete one-half of a job in an hour. Your friend can complete one-third of the same job in an hour. How long will it take to complete the job if you work together?
Answer:
Given,
You can complete one-half of a job in an hour. Your friend can complete one-third of the same job in an hour
1 1/2 + 1 1/3 = 1/x
has to be between 1/4 min to 1/6 hours. first guess is about (1/2)(1/4+1/6) = 5/24= 0.21 hours
2 + 3 = 1/x
5 = 1/x
x = 1/5 = 0.20 hours
Lesson 3.6 Converting Measures
EXPLORATION 1
Estimating Unit Conversions
Work with a partner. You are given 4 one-liter containers and a one-gallon container.
a. A full one-gallon container can be used to fill the one-liter containers, as shown below. Write a unit rate that estimates the number of liters per gallon.
b. A full one-liter container can be used to partially foll the one-gallon container, as shown below. Write a unit rate that estimates the number of gallons per liter.

c. Estimate the number of liters in 5.5 gallons and the number of gallons in 12 liters. What method(s) did you use? What other methods could you have used?
Answer:
EXPLORATION 2
Converting Units in a Rate
Work with a partner. The rate that a caterpillar moves is given in inches per minute. Using the rulers below, how can you convert the rate to centimeters per second? Justify your answer.
Answer:
The U.S. customary system is a system of measurement that contains units for length, capacity, and weight. The metric system is a decimal system of measurement, based on powers of 10, that contains units for length, capacity, and mass. Key Vocabulary U.S. customary system, p. 142 metric system,p. 142 You can use unit rates and ratio tables to convert measures within the same system and between systems.

Try It
Question 1.
Convert 48 feet to yards.
Answer: 16 yards
Explanation:
Convert from feets to yards
We know that
1 yard = 3 feet
So, 48 feet = 48/3 = 16 yards
Question 2.
Convert 7 miles to kilometers. Round to the nearest hundredth if necessary.
Answer:
Convert from miles to kilometers.
1 mile = 1.6 km
7 miles = 7 × 1.6 = 11.2 kilometers
Question 3.
Convert 20 quarts to liters. Round to the nearest hundredth if necessary.
Answer:
Convert from quarts to liters.
1 quart = 0.94 liters
20 quarts = 20 × 0.94 = 18.92 liters
Question 4.
Convert 60 kilometers per hour to miles per hour. Round to the nearest hundredth if necessary.
Answer:
Convert from kilometers per hour to miles per hour.
1 kilometer per hour = 0.621 miles per hour
60 kilometer per hour = 37.28 miles per hour
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal
Question 5.
DIFFERENT WORDS, SAME QUESTION
Which is different? Find “both” answers.

Answer:
“Find the number of inches in 5 centimeters” has different words.
CONVERTING MEASURES Copy and complete the statement. Round to the nearest hundredth if necessary.
Question 6.

Answer:
Convert from meters per minute to feet per minute.
1 meter per minute = 3.2 feet per minute
12 meter per minute = 39.37 feet per minute
Question 7.
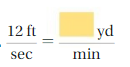
Answer:
Convert from feet per second to yard per minute
12 feet per second = 240 yard per minute
Question 8.
Will all of the water from a full two-liter bottle fit into a two-quart pitcher? Explain.
Answer:
1 liter = 1.05669 quarts
q/L = 1.05669/1
q/2 = 1.05669/1
q = 2 × 1.05669
q = 2.11338
Question 9.
DIG DEEPER!
The speed of light is about 300,000 kilometers per second. The Sun is about 93 million miles from Earth. How many minutes does it take for sunlight to reach Earth?
Answer:
Question 10.
A race car driver’s goal is to complete a 1000-kilometer auto race in 4 hours or less. The driver’s average speed is 4200 meters per minute. Does the driver meet the goal? If not, how much faster (in meters per minute) must the driver be to meet the goal?

Answer:
Converting Measures Homework & Practice 3.6
Review & Refresh
Write a unit rate for the situation.
Question 1.
102 beats per 2 minutes
Answer: 51 per minute
Explanation:
102 beats per 2 minutes
102/2 = 51 beats per minute
Question 2.
60 shirts for every 5 clothing racks
Answer: 12 for 1 clothing racks
Explanation:
60 shirts for every 5 clothing racks
60/5 = 12
12 for 1 clothing racks
Question 3.
$100 donated for every 5 volunteers
Answer: 20 for 1 volunteer
Explanation:
$100 donated for every 5 volunteers
100/5 = 20
$20 donated for 1 volunteer
Question 4.
30 milliliters every 4 hours
Answer: 7.5 ml per hour
Explanation:
30 milliliters every 4 hours
30/4 = 7.5
So, 7.5 ml per hour
Question 5.
What is the LCM of 6, 12, and 18?
A. 6
B. 18
C. 36
D. 72
Answer: C
Explanation:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 6:
6, 12, 18, 24, 30, 36, 42, 48
Multiples of 12:
12, 24, 36, 48, 60
Multiples of 18:
18, 36, 54, 72
Therefore,
LCM(6, 12, 18) = 36
Thus the correct answer is option C.
Write the prime factorization of the number.
Question 6.
56
Answer: 2 x 2 x 2 x 7
Explanation:
56 = 2 × 28
= 2 × 2 × 14
= 2 × 2 × 2 × 7
Thus the prime factorization of the number 56 is 2 x 2 x 2 x 7
Question 7.
74
Answer: 2 × 37
Explanation:
74 = 2 × 37
Thus the prime factorization of the number 74 is 2 x 37
Question 8.
63
Answer: 3 × 3 × 7
Explanation:
63 = 3 × 21
= 3 × 3 × 7
Thus the prime factorization of the number 63 is 3 × 3 × 7
Question 9.
132
Answer: 2 x 2 x 3 x 11
Explanation:
132 = 2 × 66
= 2 × 2 × 33
= 2 × 2 × 3 × 11
Thus the prime factorization of the number 132 is 2 x 2 x 3 x 11
Write the product as a power.
Question 10.
6 × 6
Answer: The product of 6×6 is 6²
Question 11.
18 × 18 × 18 × 18
Answer: The product of 18×18×18×18 is 18⁴
Question 12.
12 × 12 × 12 × 12 × 12
Answer: The product of 12×12×12×12×12 is 12⁵
Concepts, Skills, & Problem Solving
COMPARING MEASURES Answer the question. Explain your answer. (See Explorations 1 & 2, p. 141.)
Question 13.
Which juice container is larger: 2 L or 1 gal?
Answer:
Convert from liters to gal
1 liter = 0.26 gal
2 liter = 0.52 gal
1 gal = 3.78 liter
Thus the juice container with 1 gal is larger
Question 14.
Which is longer:1 in. or 2 cm?
Answer: 1 inch is longer than 2 cm
Explanation:
Convert from inches to cm
1 inch = 2.54 cm
2.54 cm > 2 cm
CONVERTING MEASURES Copy and complete the statement.
Question 15.
![]()
Answer: 6 cups
Explanation:
Convert from pints to cups.
1 pint = 2 cups
3 pints = 3 × 2 cups = 6 cups
Question 16.
![]()
Answer: 1.5 L
Explanation:
Convert from mL to L
1000 mL = 1 L
1500 mL = 1.5 L
Question 17.
![]()
Answer: 2.5 lb
Explanation:
Convert from ounces to lb
1 ounce = 0.0625
40 oz = 2.5 lb
Question 18.
![]()
Answer: 60 in.
Explanation:
Convert from feet to inches.
1 feet = 12 inches
5 feet = 5 × 12 = 60 inches
So, 5 ft = 60 in.
Question 19.
![]()
Answer: 24 qt
Explanation:
Convert from gallons to quarts
1 gal = 4 qt
6 gal = 6 × 4 qt = 24 qt
So, 6 gal = 24 qt
Question 20.
![]()
Answer: 480 mm
Explanation:
Convert from cm to mm
1 cm = 10 mm
48 cm = 48 × 10 mm = 480 mm
So, 48 cm = 480 mm
Question 21.
![]()
Answer: 5 m
Explanation:
Convert from cm to m
1 cm = 0.01 m
500 cm = 500 × 0.01 m = 5 meters
So, 500 cm = 5 meters
Question 22.
![]()
Answer: 6
Explanation:
Convert from grams to kilograms
1 kg = 1000 g
6000g = 6 kg
Question 23.
![]()
Answer:
Explanation:
Convert from fl ounce to cups
1 fl oz = 0.125 cups
32 fl ouz = 4 cups
CONVERTING MEASURES Copy and complete the statement. Round to the nearest hundredth if necessary.
Question 24.
![]()
Answer: 13 qt
Explanation:
Convert from liters to quarts.
1 L = 1.05 qt
12 L = 12.608 qt
12 L ≈ 13 qt
Question 25.
![]()
Answer: 46 ft
Explanation:
Convert from meters to feet
1 meter = 3.28 feet
14 meter = 45.93 feet
14 m ≈ 46 feet
Question 26.
![]()
Answer: 1 m
Explanation:
Convert from feet to meter
1 feet = 0.3 m
4 feet = 1.21 m
4 ft ≈ 1 m
Question 27.
![]()
Answer: 29 kg
Explanation:
Convert from lb to kgs.
1 lb = 0.45 kg
64 lb = 29.02 kg
64 lb ≈ 29 kg
Question 28.
![]()
Answer: 0.186 mi
Explanation:
Convert from kg to miles
1 km = 0.621 miles
0.3 km = 0.186 miles
Question 29.
![]()
Answer: 191 cm
Explanation:
Convert from inches to centimeters.
1 inch = 2.54 centimeter
75.2 inch = 191.008 centimeter
75.2 in ≈ 191 cm
Question 30.
![]()
Answer: 34 lb
Explanation:
Convert from kg to lb
1 kg = 2.20 lb
17 kg = 37.47 lb
17 kg ≈ 34 lb
Question 31.
![]()
Answer: 6 inches
Explanation:
Convert from cm to inches.
1 cm = 0.39 in
15 cm = 5.90 in
15 cm ≈ 6 in
Question 32.
![]()
Answer: 14 km
Explanation:
Convert from miles to kilometers
1 mile = 1.609 km
9 miles = 14.48 km
9 miles ≈ 14 km
Question 33.
GRAPHING RELATIONSHIPS
Represent the relationship between each pair of units in a coordinate plane.
a. feet and yards
b. pounds and kilograms
Answer:
Question 34.
MODELING REAL LIFE
Earth travels 30 kilometers each second as it revolves around the Sun. How many miles does Earth travel in 1 second?
Answer:
Question 35.
MODELING REAL LIFE
The Mackinac Bridge in Michigan is the third-longest suspension bridge in the United States.
a. How high above the water is the roadway in meters?
b. The bridge has a length of 26,372 feet. What is the length in kilometers?

Answer:
USING CONVERSION FACTORS Copy and complete the statement. Round to the nearest hundredth if necessary.
Question 36.
![]()
Answer: 90 gal
Explanation:
Convert from cubic feet to the gallon
1 cu ft = 7.48 gal
12 cu ft = 12 × 7.48 gal = 89.76 gal
12 cu ft ≈ 90 gal
Question 37.
![]()
Answer: 6 L
Explanation:
Convert from quart to liter
1 qt = 0.94 L
6 qt = 5.67 L
6 qt ≈ 6 L
Question 38.
![]()
Answer: 1 gal
Explanation:
Convert from liters to gal
1 L = 0.264 gal
5 L = 5 × 0.264 gal = 1.32 gal
5 L ≈ 1 gal
Question 39.
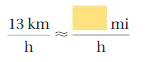
Answer: 8 miles per hour
Explanation:
Convert from km per hour to miles per hour
1 km per hour = 0.621 miles per hour
13 km per hour = 8.07 miles per hour
Question 40.
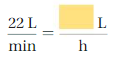
Answer: 1320 liter per hour
Explanation:
Convert from liter per minute to liter per hour
1 liter per minute = 60 liter per hour
22 liter per minute = 1320 liter per hour
Question 41.

Answer: 0.175 miles per second
Explanation:
Convert from miles per hour to miles per second.
1 miles per hour = 0.0002 miles per second
63 miles per hour = 0.175 miles per second
Question 42.
YOU BE THE TEACHER
Your friend converts 8 liters to quarts. Is your friend correct? Explain your reasoning.
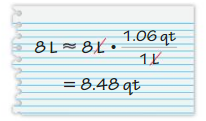
Answer:
Convert from liters to quarts
1 liter = 1.05 qt
8 liter = 8.45 qt (approx)
Yes, your friend is correct.
Question 43.
MODELING REAL LIFE
The diagram shows the number of quarts of blood the human heart pumps per minute.
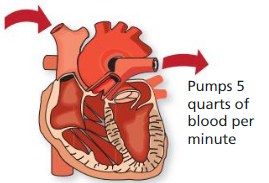
a. How many quarts of blood does the human heart pump per hour?
Answer:
1 hour = 60 minutes
The heart pumps 5 quarts of blood per minute
1 min = 5 quarts
60 min = 60 × 5 quarts = 300 quarts
Thus the heart pumps 300 quarts of blood per hour.
b. How many liters of blood does the human heart pump per minute?
Answer:
Given,
The heart pumps 5 quarts of blood per minute
Convert from quarts to liters
1 quart = 0.94 L
5 quarts = 4.73 L
Thus it pumps 4.73 L of blood per minute.
Question 44.
PROBLEM SOLVING
After washing dishes, water drips from the faucet. The graph shows the number of cups of water that drip from the faucet over time. How many gallons of water drip from the faucet in 24 hours?
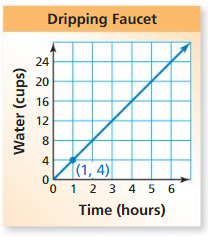
Answer:
COMPARING MEASURES Copy and complete the statement using < or >.
Question 45.
![]()
Answer: <
Explanation:
Convert from ounce to kg
1 oz = 0.02kg
30 oz = 0.85kg
Thus 30 oz < 8 kg
Question 46.
![]()
Answer: <
Explanation:
Convert from feet to centimeter
1 feet = 30.48 cm
6 feet = 182.88
Thus 6 feet < 300 cm
Question 47.
![]()
Answer: >
Explanation:
Convert from gal to liter
1 gal = 3.78L
3 gal = 11.35L
Thus 3 gal > 6L
Question 48.
![]()
Answer: >
Explanation:
Convert from inches to mm.
1 in = 25.4mm
10 in = 254 mm
Thus 254mm > 200 mm
Question 49.
![]()
Answer: >
Explanation:
Convert from lb to grams
1 lb = 453.5g
5 lb = 2268g
2268g > 1200g
Thus 5 lb > 1200g
Question 50.
![]()
Answer: >
Explanation:
Convert from meters to feet
1 meter = 3.28 ft
1500 meter = 4921.26 ft
4921.26 ft > 3000 ft
Thus 1500 m > 3000 ft
USING DERIVED UNITS Copy and complete the statement. Round to the nearest hundredth if necessary.
Question 51.
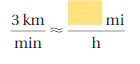
Answer: 112 miles per hour
Explanation:
Convert from km per min to miles per hour
1 km per min = 37.28 miles per hour
3 km per min = 111.84 miles per hour
3 km per min ≈ 112 miles per hour
Question 52.
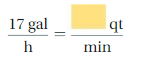
Answer: 1.13 qt per minute
Explanation:
Convert from gal per hour to qt per minute
1 gal per hour = 0.06 qt per minute
17 gal per hour = 1.13 qt per minute
Question 53.

Answer: 4 inches per second
Explanation:
Convert from cm per minute to inches per second
1 cm per minute = 0.006 inches per second
600 cm per minute = 3.93 inches per second
600 cm per minute ≈ 4 inches per second
Question 54.
MODELING REAL LIFE
You are riding on a zip line. Your speed is 15 miles per hour. What is your speed in feet per second?
Answer: 22 feet per second
Explanation:
Given,
You are riding on a zip line. Your speed is 15 miles per hour.
Convert from mile per hour to feet per second
1 mile per hour = 1.46 feet per second
15 miles per hour = 22 feet per second
Question 55.
PROBLEM SOLVING
Thunder is the sound caused by lightning. You hear thunder 5 seconds after a lightning strike. The speed of sound is about 1225 kilometers per hour. About how many miles away was the lightning?
Answer:
Question 56.
PROBLEM SOLVING
Boston, Massachusetts, and Buffalo, New York, are hit by snowstorms that last 3 days. Boston accumulates snow at a rate of 1.5 feet every 36 hours. Buffalo accumulates snow at a rate of 0.01 inch every minute. Which city accumulates more snow in 3 days? How much more snow?

Answer:
Question 57.
DIG DEEPER!
You travel 4000 feet every minute on a snowmobile.
a. The evening speed limit for snowmobiles in your state is 55 miles per hour. Is your speed less than or equal to the speed limit? Justify your answer.
b. What is your pace in minutes per mile?
c. You are 22 miles from your house at 6:00 P.M. If you continue to travel at this speed, do you reach your house in time for dinner at 6:30 P.M.?
Answer:
Question 58.
REASONING
The table shows the flying speeds of several birds.

a. Which bird is the fastest? Which is the slowest?
b. The peregrine falcon has a dive speed of 322 kilometers per hour. Is the dive speed of the peregrine falcon faster than the flying speed of any of the birds? Explain.
Answer:
Question 59.
STRUCTURE
Consider the conversion facts 1 inch = 2.54 centimeters and 1 centimeter ≈ 0.39 inch.
a. Write an expression for the exact number of inches in 1 centimeter.
b. Use a calculator to evaluate your expression in part(a). Explain why measurement conversions may be slightly different when converting between metric units and U.S. customary units using the conversion facts in the back of the book.
Answer:
Question 60.
DIG DEEPER!
One liter of paint covers 100 square feet. How many gallons of paint does it take to cover a room whose walls have an area of 800 square meters?
Answer:
Given,
One liter of paint covers 100 square feet.
First, convert 800 square meters to square feet. I calculated it to be 8611.13 sq ft
100 sq.ft/1 L x L = 8611.13.
Now convert L to gallons.
1gallon = 3.785 L
Ratios and Rates Connecting Concepts
Using the Problem-Solving Plan
Question 1.
You mix water, glue, and borax in the ratio of 3 : 1 : 2 to make slime. How many gallons of each ingredient should you use to make 0.75 gallon of slime?

Understand the problem.
You know the ratio of the ingredients in the slime and that you are making 0.75 gallon of slime. You are asked to find the number of gallons of each ingredient needed to make 0.75 gallon of slime.
Make a plan.
Represent the ratio 3 : 1 : 2 using a tape diagram. Because there are 6 parts that represent 0.75 gallon, divide 0.75 by6 to find the value of one part of the tape diagram. Then use the value of one part to find the number of gallons of each ingredient you should use.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
Question 2.
You buy yogurt cups and frozen fruit bars for a party. Yogurt cups are sold in packages of six. The ratio of the number of yogurt cups in a package to the number of frozen fruit bars in a package is 3 : 2. What are the least numbers of packages you should buy in order to have the same numbers of yogurt cups and frozen fruit bars?

Answer:
Question 3.
The greatest common factor of two whole numbers is 9. The ratio of the greater number to the lesser number is 6 : 5. What are the two numbers? Justify your answer.
Answer:
Performance Task
Oops! Unit Conversion Mistakes
At the beginning of this chapter, you watched a STEAM Video called “Human Circulatory System.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Ratios and Rates Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.

Graphic Organizers
You can use a Definition and Example Chart to organize information about a concept. Here is an example of a Definition and Example Chart for the vocabulary term ratio.

Choose and complete a graphic organizer to help you study the concept.

1. value of a ratio
2. equivalent ratios
3. tape diagram
4. ratio table
5. rate
6. unit rate
7. conversion factor
Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

3.1 Ratios (pp. 107–114)
Learning Target: Understand the concepts of ratios and equivalent ratios.
Write the ratio.
Question 1.
butterflies : caterpillars

Answer: 3 : 2
Explanation:
There are 3 butterflies and 2 caterpillars
Thus the ratio is 3 : 2
Question 2.
saxophones : trumpets

Answer: 6 : 3
Explanation:
There are 6 saxophones and 3 trumpets
Thus the ratio is 6: 3 and the equivalent ratio is 1 : 2
Question 3.
The ratio of hydrogen atoms to nitrogen atoms in a container is 2 : 3.

a. Find and interpret the value of the ratio.
b. In another container, the number of hydrogen atoms is 3 times the number of nitrogen atoms. Write the ratio of hydrogen atoms to nitrogen atoms.
Answer:
Determine whether the ratios are equivalent.
Question 4.
5 : 2 and 30 : 12
Answer: Yes
Explanation:
30/12 = 5/2
5 : 2 = 5 : 2
Thus the ratios are equivalent
Question 5.
4 : 3 and 8 : 7
Answer: No
Explanation:
4/3 ≠ 8/7
Thus the ratios are not equivalent
Question 6.
6 : 4 and 18 : 6
Answer: No
Explanation:
6 : 4 and 18 : 6
6/4 = 3/2
18/6 = 3
3/2 ≠ 3
Thus the ratios are not equivalent
Question 7.
18 : 12 and 3 : 2
Answer: Yes
Explanation:
18 : 12 and 3 : 2
18/12 = 3/2
3 : 2 = 3 : 2
Thus the ratios are equivalent
Question 8.
Write two equivalent ratios that have values of \(\frac{5}{7}\)
Answer: \(\frac{10}{14}\) and \(\frac{15}{21}\)
Question 9.
During a chess match, there are 12 pieces left on the board. The ratio of white pieces to black pieces is 2 : 1. How many white pieces are on the board?
Answer:
Question 10.
You run at a pace of 2 miles every 17 minutes. Your friend runs at a pace of 3 miles every 24 minutes. Are you and your friend running at the same pace? If not, who is running faster?
Answer:
3.2 Using Tape Diagram (pp. 115-120)
Learning Target: Use tape diagrams to model and solve ratio problems.
The tape diagram represents the ratio of the time you spend reading to the time your friend spends reading. You read for 8 hours. How many hours does your friend spend reading?
Question 11.
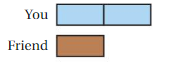
Answer:
Question 12.
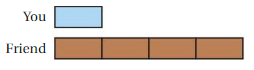
Answer:
Question 13.
The tape diagram represents the ratio of customers to guides on a mountain climbing trip. There are 6 guides on the trip. How many customers are on the trip?
Answer:
A container has peppermint gum and spearmint gum. You are given the number of pieces of peppermint gum in the container and the ratio of peppermint gum to spearmint gum. Find the number of pieces of spearmint gum in the container.
Question 14.
24 peppermint; 8 to 5
Answer:
Let the total number of peppermint gum and spearmint gum in the container = x
The ratio is 8 : 5
8 + 5 = 13
8/13 × x = 24
x = 24 × 13/8
x = 39
5/13 × 39 = 15
Question 15.
18 peppermint; 2 : 3
Answer:
Let the total number of peppermint gum and spearmint gum in the container = x
The ratio is 2 : 3
2 + 3 = 5
2/5 × x = 18
x = 18 × 5/2
x = 45
Number of spearmint gum will be now
Ratio of spearmint/total ratio × total number of gums = number of spearmint
3/5 × 45 = 27
Thus the number of spearmint gum = 27
Question 16.
32 peppermint; 8 to 7
Answer:
Let the total number of peppermint gum and spearmint gum in the container = x
The ratio is 8 : 7
8 + 7 = 15
8/15 × x = 32
x = 32 × 15/8
x = 4 × 15
x = 60
Number of spearmint gum will be now
Ratio of spearmint/total ratio × total number of gums = number of spearmint
7/15 × 60 = 28
Question 17.
40 peppermint; 5 : 2
Answer:
Let the total number of peppermint gum and spearmint gum in the container = x
The ratio is 5 : 2
5 + 2 = 7
5/7 × x = 40
x = 40 × 7/5
x = 8 × 7
x = 56
Number of spearmint gum will be now
Ratio of spearmint/total ratio × total number of gums = number of spearmint
2/7 × 56 = 16
A theater sells adult tickets and student tickets. You are given the total number of tickets sold and the ratio of adult tickets sold to student tickets sold. How many of each type of ticket are sold?

Question 18.
120 tickets; 6 to 4
Answer:
The ratio of adult tickets sold to student tickets sold is 6 : 4
6 + 4 = 10
6/10 = x/120
6 × 120 = x × 10
10x = 720
x = 720/10 = 72
x = 72
The number of student tickets would be 120 – 72 = 48 student tickets
Question 19.
165 tickets; 8 to 7
Answer:
The ratio of adult tickets sold to student tickets sold is 8 : 7
8 + 7 = 15
8/15 = x/165
8 × 165 = x × 15
1320 = 15x
x = 1320/15
x = 88
The number of student tickets would be 165 – 88 = 77 student tickets
Question 20.
210 tickets; 16 : 5
Answer:
The ratio of adult tickets sold to student tickets sold is 16 : 5
16 + 5 = 21
16/21 = x/210
16 × 210 = x × 21
3360 = 21x
x = 3360/21
x = 160
The number of student tickets would be 210 – 160 = 50 student tickets
Question 21.
248 tickets; 5 : 3
Answer:
The ratio of adult tickets sold to student tickets sold is 5 : 3
5 + 3 = 8
5/8 = x/248
5 × 248 = 8 × x
1240 = 8x
x = 1240/8
x = 155
The number of student tickets would be 248 – 155 = 93 student tickets
Question 22.
You perform 7 sit-ups for every 2 pull-ups as part of an exercise routine. You perform 25 more sit-ups than pull-ups. How many sit-ups and how many pull-ups do you perform?
Answer: 35 sit ups and 10 pullups
Explanation:
Given,
You perform 7 sit-ups for every 2 pull-ups as part of an exercise routine.
You perform 25 more sit-ups than pull-ups.
so we know that for 7 situps you do 2 pullups
so the possible values would be
7,2
14,4
21, 6
28, 8
35, 10, and so on
so now you just look at which two numbers have a difference of 25
when subtracting them, you’ll notice that 35 and 10 have a difference of 25.
3.3 Using Ratio Tables (pp. 121-128)
Learning Target: Use ratio tables to represent equivalent ratios and solve ratio problems.
Find the missing values in the ratio table. Then write the equivalent ratios.
Question 23.
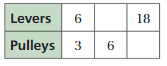
Answer:
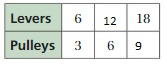
Question 24.
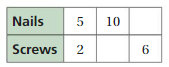
Answer:
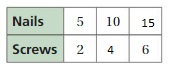
Question 25.
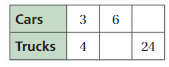
Answer:
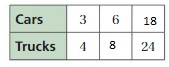
Question 26.
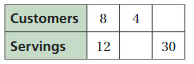
Answer:
Find the missing quantity in the double number line.
Question 27.
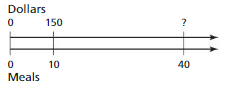
Answer:
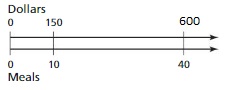
Question 28.
Answer:
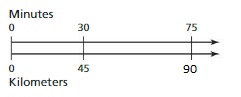
Question 29.
Use all four operations to complete the ratio table. Justify your answer.
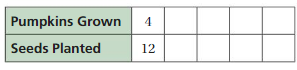
Answer:
Question 30.
A song has 12 beats every 5 seconds. How many beats are there in 30 seconds?
Answer: 72 beats in 30 seconds
Explanation:
Given,
A song has 12 beats every 5 seconds.
5 seconds = 12 beats
1 second = 12/5 = 2.4 beats
30 seconds = 30 × 2.4 beats = 72 beats
Thus 72 beats are there in 30 seconds.
Question 31.
On New Year’sEve, the Times Square ball is lowered 47 feet every 20 seconds. How long does it take for the ball to be lowered 141 feet?
Answer: 60 seconds
Explanation:
On New Year’sEve, the Times Square ball is lowered 47 feet every 20 seconds.
All you have to do is cross multiply and isolate x.
47/20 × 141/x
47x = 2820
x = 60 seconds
Question 32.
Welder A charges $300 for every 4 hours of labor. Welder B charges $240 for every 3 hours of labor. Which welder offers a better deal?

Answer:
Welder A has a better deal because for each hour welder A would charge $75 while welder B would charge $80
Welder A:
300/4 = $75
Welder B:
240/3 = $80
Question 33.
You make lemonade by adding 11 cups of water for every 3 cups of lemon juice. Your friend makes lemonade by adding 9 cups of water for every 2 cups of lemon juice. Whose lemonade is more watered down?
Answer:
Well first I did was I found out that both 3 and 2 go into 12.
2 goes into 12 6 times. 9 × 6 is 54.
3 goes into 12 four times.
11 × 4 is 44.
54 is greater than 44 therefore the answer would be your friend.
3.4 Graphing Ratio Relationships (pp. 129-134)
Learning Target: Represent ratio relationships in a coordinate plane.
Represent the ratio relationship using a graph.
Question 34.
Answer:
Question 35.
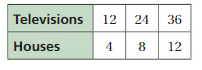
Answer:
Question 36.
You buy magnesium sulfate for $1.50 per pound.
a. Represent the ratio relationship using a graph.
b. How much does 3.5 pounds of magnesium sulfate cost?
Answer:
Question 37.
A 5-ounce can of tuna costs $0.90. A 12-ounce can of tuna costs $2.40. Graph each ratio relationship in the same coordinate plane. Which is the better buy?

Answer:
3.5 Rates and Unit Rates (pp. 135–140)
Learning Target: Understand the concept of a unit rate and solve rate problems.
Write a unit rate for the situation.
Question 38.
12 stunts in 4 movies
Answer: 3
Explanation:
12 stunts in 4 movies
12/4 = 3
3 stunts in 1 movie
Question 39.
3600 stitches in 3 minutes
Answer: 1200
Explanation:
3600 stitches in 3 minutes
3600/3 = 1200
1200 stiches in 1 minute
Question 40.
$18 for 6 pounds
Answer: 3
Explanation:
$18 for 6 pounds
18/6 = 3
$3 for 1 pound
Question 41.
240 people in 5 buses
Answer: 48
Explanation:
240 people in 5 buses
240/5 = 48
48 people in 1 bus
Question 42.
A train travels 120 miles in 3 hours. Write two unit rates that describe the relationship between the number of miles and the number of hours the train travels.
Answer:
Question 43.
Mercury orbits the Sun 3 times in 264 days.
a. How many times does Mercury orbit the Sun in 440 days?
b. How many days does it take Mercury to orbit the Sun 8 times?
Answer:
Question 44.
A cyclist travels 4 miles in 20 minutes. At this rate, how many miles does the cyclist travel in 30 minutes?
Answer:
Given,
A cyclist travels 4 miles in 20 minutes.
20/4 = 5 minutes
1 mile in 5 minutes
30 minutes divided by 5
30/5 = 6 minutes
So, 6 miles in 6 minutes
Decide whether the rates are equivalent.
Question 45.
18 keystrokes in 3 seconds
48 keystrokes in 16 seconds
Answer: No
Explanation:
18 keystrokes in 3 seconds
48 keystrokes in 16 seconds
18 : 3 :: 48 : 16
6 : 1 :: 3 : 1
The rates are not equivalent
Question 46.
210 miles in 3 hours
780 miles in 12 hours
Answer: No
Explanation:
210 miles in 3 hours
780 miles in 12 hours
210 : 3 = 70
780 : 12 = 65
The rates are not equivalent
Question 47.
You and a friend are picking up trash on a beach. You fill 2 bags with trash in 28 minutes. Your friend fills 3 bags with trash in 48 minutes. Who fills bags with trash faster? How much sooner will the faster person fill 7 bags with trash?

Answer:
Divide 28 minutes by the 2 bags of trash.
You fill 1 bag of trash every 14 minutes.
28 ÷ 2 = 14
Your friend fills 1 bag of trash every 16 minutes.
48 ÷ 3 = 16
7 bags × 16 min = 105 min
7 bags × 14 min = 98 min
105 – 98 = 7 minutes
3.6 Converting Measures (pp. 141–148)
Learning Target: Use ratio reasoning to convert units of measure.
Copy and complete the statement. Round to the nearest hundredth if necessary.
Question 48.
![]()
Answer: 20 fl. oz
Explanation:
Convert from cups to fluid ounces
1 cup = 8 fluid ounce
2.5 cups = 20 fluid ounces
Question 49.
![]()
Answer: 4 yd
Explanation:
Convert from feet to yards
1 feet = 0.33 yard
12 feet = 4 yards
Question 50.
![]()
Answer: 3.5
Explanation:
Convert from milligrams to grams
1 mg = 0.001 g
3500 mg = 3.5 grams
Question 51.
![]()
Answer:
Convert from liters to quarts
1 L = 1.05 qt
3 L = 3.17 qt
Thus 3 L ≈ 3 qt
Question 52.
![]()
Answer: 23 cm
Explanation:
Convert from inches to centimeters
1 in = 2.54 cm
9.2 in = 23.36 cm
9.2 in ≈ 23 cm
Question 53.
![]()
Answer: 7 kg
Explanation:
Convert from lb to kg
1 lb = 0.45 kg
15 lb = 6.80 kg
15 lb ≈ 7 kg
Question 54.
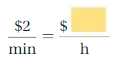
Answer: $120
Explanation:
Convert from hours to minutes
1 hour = 60 minutes
1 min = $2
60 min = x
x = 60 × 2
x = $120
Question 55.
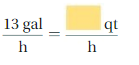
Answer: 52
Explanation:
Convert from gal to qt
1 gal = 4 qt
13 gal = 52 qt
Question 56.
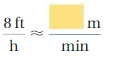
Answer: 0.040
Question 57.
Explain how to use conversion factors to find the number of fluid ounces in any given number of quarts of a liquid.
Answer:
Question 58.
Water flows through a pipe at a rate of 10 gallons per minute. How many gallons of water flow through the pipe in an hour?
Answer:
Given,
Water flows through a pipe at a rate of 10 gallons per minute.
1 hour = 60 minute
1 minute = 10 gallon
60 minutes = 60 × 10 gallon = 600 gallon
Thus 600 gallons of water flow through the pipe in an hour.
Question 59.
Germany suggests a speed limit of 130 kilometers per hour on highways. Is the speed shown greater than the suggested limit?

Answer:
Question 60.
The distance between two stars increases at a rate of 3 centimeters per month. What is the rate in inches per year?
Answer: 14.17 inches
Explanation:
Given,
The distance between two stars increases at a rate of 3 centimeters per month.
3 cm – 1 month
1 year = 12 months
3 × 12 = 36 centimeters
Convert from centimeters to inches
36 centimeters = 14.17 inches
Ratios and Rates Practice Test
Question 1.
Write the ratio of scooters to bikes.

Answer:
There are 3 scooter and 3 bikes
Thus the ratio of scooters to bikes is 3 : 3
Question 2.
Determine whether the ratios 8 : 7 and 15 : 14 are equivalent.
Answer: The ratios 8 : 7 and 15 : 14 are not equivalent.
The equivalent ratio of 8:7 is 16 : 14.
Find the missing values in the ratio table. Then write the equivalent ratios.
Question 3.
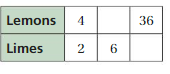
Answer:
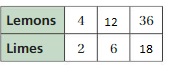
The missing values are 12, 18
The ratio is 2:1
The equivalent ratio of 2 : 1 is 12 : 6 and 36 : 18
Question 4.
Answer:
The missing values are 54, 10
The ratio is 2 : 9
The equivalent ratio of 2 : 9 is 12 : 54 and 10 : 45
Question 5.
Represent the ratio relationship using a graph.
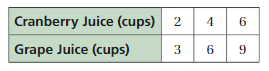
Answer:
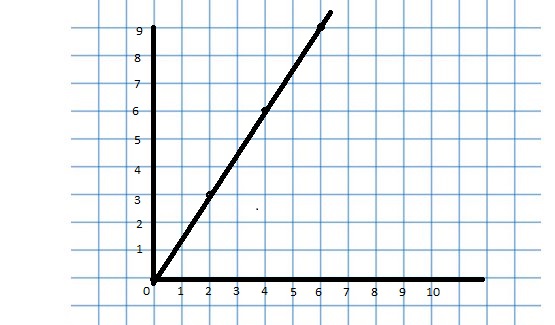
Question 6.
You travel 224 miles in 4 hours. Find the unit rate.
Answer: 56
Explanation:
Given,
You travel 224 miles in 4 hours.
1 hour = x
4 × x = 224
x = 224/4
x = 56 miles
The unit rate is 56 miles.
Copy and complete the statement. Round to the nearest hundredth if necessary.
Question 7.
![]()
Answer:
![]()
Explanation:
Convert from centimeters to inches.
1 cm = 0.39
6 cm = 6 × 0.39
6 cm = 2.34 inches
Question 8.
![]()
Answer:
![]()
Explanation:
Convert from liters to gal
1 liter = 0.26 gal
30 liter = 7.92 gal
Question 9.
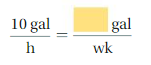
Answer:
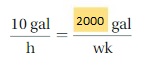
Explanation:
Convert from hours to week
1 hour = 0.005 = 5/1000
10 gal/h = 2000/wk
Question 10.
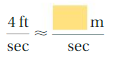
Answer:
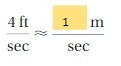
Explanation:
Convert from feet to meters
1 feet = 0.30m
4 feet = 1.21 m
4 ft ≈ 1m
Question 11.
During a baseball season, Team A scores 9 runs for every 7 runs that Team B scores. The total number of runs scored by both teams is 1440. How many runs does each team score?
Answer:
Team A scores 810
Team B scores 630
Explanation:
During a baseball season, Team A scores 9 runs for every 7 runs that Team B scores.
The total number of runs scored by both teams is 1440.
Let b scores x runs
Then a scores x + (2 × x/7)
Because every 7 runs of b, a is scores more 2 runs.
Total number of runs scored by both teams is 1440
a + b = 1440
x + (2 × x/7) + x = 1440
(16 × x)/7 = 1440
16 × x = 1440 × 7
16x = 10080
x = 10080/16
x = 630
Thus team b scores 630 runs
Team a scores is x + (2 × x/7) = 810 runs
Question 12.
At a movie theater, the ratio of filled seats to empty seats is 6 : 5. There are 120 empty seats. How many seats are filled?
Answer: 144
Explanation:
Given,
At a movie theater, the ratio of filled seats to empty seats is 6 : 5. There are 120 empty seats.
Number of filled = 6
Number of empty = 5
120/5 = 24 then multiply it by 6 to get 144.
Thus the number of filled seats = 144
Question 13.
You and your friend mix water and citric acid. You add 3 cups of citric acid for every 16 cups of water. Your friend adds 2 cups of citric acid for every 12 cups of water. Whose mixture is more acidic?
Answer: A’s mixture is more acidic
Explanation:
Given,
You and your friend mix water and citric acid.
You add 3 cups of citric acid for every 16 cups of water.
Your friend adds 2 cups of citric acid for every 12 cups of water.
A add 3 cups of citric acid for every 16 cups of water, the ratio = 3/16
B adds 2 cups of citric acid for every 12 cups of water = 2/12
LCM of 16 and 12 are 48
16 – 16, 32, 48, 64, 80, 96
12 – 12, 24, 36, 48, 60, 72
A – 3/16 × 3/3 = 9/48
B – 2/12 × 4/4 = 8/48
We found that in terms of 48 cups of water, friend A mixes 9 cups of acid while friend B mixes 8 cups of acid, means A is adding more acid than B and hence friend A’s mixture is more acidic.
Question 14.
Determine which windsurfer is faster. Explain your reasoning.

Answer: The second windsurfer is faster than the first windsurfer.
First convert from meter to feet
1 meter = 3.28
5 meter = 16.40
Convert from minute to second
1 min = 60 sec
16.40 × 60 = 984 feet
984 feet is greater than 720 feet
Question 15.
In a rectangle, the ratio of the length to the width is 5 : 2. The length of the rectangle is 13.875 feet greater than the width. What are the perimeter and the area of the rectangle?
Answer:
P = 64.75 feet
A = 213.91 feet
Explanation:
Given,
In a rectangle, the ratio of the length to the width is 5 : 2.
The length of the rectangle is 13.875 feet greater than the width.
13.875 ÷ 3 = 4.625 feet
4.625 × 5 = 23.125 feet
So, the length of the rectangle is 23.125 feet
4.625 × 2 = 9.25 feet
So, the width of the rectangle is 9.25 feet
We know that, Perimeter of the rectangle = 2l + 2w
P = 2(23.125) + 2(9.25)
P = 64.75 feet
Area of the rectangle = l × w
A = 23.125 × 9.25
Area = 213.91 sq. feet
Ratios and Rates Cumulative Practice

Question 1.
Which number is equivalent to \(\frac{2}{9}\) ÷ \(\frac{4}{5}\)?
A. \(\frac{8}{14}\)
B. \(\frac{5}{18}\)
C. \(\frac{7}{13}\)
D. 3\(\frac{3}{5}\)
Answer: \(\frac{5}{18}\)
Explanation:
Dividing two fractions is the same as multiplying the first fraction by the reciprocal (inverse) of the second fraction.
Take the reciprocal of the second fraction by flipping the numerator and denominator and changing the operation to multiplication. Then the equation becomes
\(\frac{2}{9}\) × \(\frac{5}{4}\) = \(\frac{10}{36}\)
This fraction can be reduced by dividing both the numerator and denominator by the Greatest Common Factor of 10 and 36 using
GCF is 2
\(\frac{10}{36}\) ÷ \(\frac{2}{2}\) = \(\frac{5}{18}\)
Thus the correct answer is option B.
Question 2.
Your speed while waterskiing is 22 miles per hour. How fast are you traveling in kilometers per hour? Round your answer to the nearest hundredth.

Answer: 35 kilometers
Explanation:
Given,
Your speed while waterskiing is 22 miles per hour.
Convert from miles to kilometers
1 mile = 1.609 kilometer
22 miles = 22 × 1.609 = 35.40 kilometers
Question 3.
Which number is equivalent to the expression below?
2 . 42 + 3(6 ÷ 2)
F. 25
G. 41
H. 73
I. 105
Answer:
2 . 42 + 3(6 ÷ 2)
2 . 42 + 3(3)
2 . 42 + 9
2 × 16 + 9
32+9 = 41
Thus the correct answer is option G.
Question 4.
The tape diagram models the ratio of red beads to green beads in a bracelet. The bracelet uses 12 red beads. How many green beads are in the bracelet?
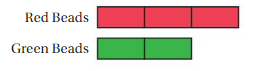
A. 4 green beads
B. 8 green beads
C. 12 green beads
D. 20 green beads
Answer: 8 green beads
Explanation:
Given,
The tape diagram models the ratio of red beads to green beads in a bracelet. The bracelet uses 12 red beads.
From the above figure we observe that there are 3
3 × 4 = 12
1 box = 4 beads
There are 2 green boxes
2 × 4 = 8
Thus there 8 green beads in the bracelet.
Question 5.
What is the least common multiple of 8, 12, and 20?
F. 24
G. 40
H. 60
I. 120
Answer: 120
Explanation:
Find and list multiples of each number until the first common multiple is found. This is the lowest common multiple.
Multiples of 8:
8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96, 104, 112, 120, 128, 136
Multiples of 12:
12, 24, 36, 48, 60, 72, 84, 96, 108, 120, 132, 144
Multiples of 20:
20, 40, 60, 80, 100, 120, 140, 160
Therefore,
LCM(8, 12, 20) = 120
Thus the correct answer is option I.
Question 6.
Which number is equivalent to 2.34 × 1.08 × 5.6?
A. 12.787632
B. 14.15232
C. 23.5872
D. 14,152.32
Answer: 14.15232
Explanation:
Multiply the three numbers
2.34 × 1.08 × 5.6 we get 14.15232
Thus the correct answer is option B.
Question 7.
The school store sells 4 pencils for $0.50. At this rate, what is the cost (in dollars) of 10 pencils?

Answer: $1.25
Explanation:
Given,
The school store sells 4 pencils for $0.50.
Cost of 1 pencil is 0.50/4 = 0.125
0.125 × 10 = 1.25
Thus the cost of 10 pencils is $1.25
Question 8.
A factor tree for 14,700 is shown. Which factor of 14,700 is not a perfect square?
F. 25
G. 49
H. 196
I. 588
Answer:
The given number is 14700
Now we prime factorize the number.
14700 = 147 × 100
= 7 × 21 × 10 × 10
= 7 × 7 × 3 × 5 × 2 × 5 × 2
= 2 × 2 × 3 × 5 × 5 × 7 × 7
We see that each of 2, 5 and 7 appears twice in the factorization. But 3 appears only once, for which the number 14700 is not a perfect square.
∴ we divide 14700 by 3 to get a perfect square.
∴ the perfect square number is
= 14700 ÷ 3
= 4900
= 70²
588 is not a perfect square
Thus the correct answer is option I.
Question 9.
Which of the following is a ratio of frogs to snakes?

A. 4 : 8
B. 8 : 12
C. 8 : 4
D. 4 : 12
Answer: 8:4
Explanation:
By seeing the above figure we can write the ratio from frogs to snakes.
There are 8 frogs
There are 4 snakes
8:4
Thus the correct answer is option C.
Question 10.
Which expression is equivalent to 36?
F. 3 × 3 × 3 × 3 × 3
G. 3 × 5
H. 5 × 5 × 5
I. 3 + 3 + 3 + 3 + 3
Answer: 3 × 3 × 3 × 3 × 3
The expression equivalent to 36 is 3 × 3 × 3 × 3 × 3
Thus the correct answer is option F.
Question 11.
Which is the correct order of operations when evaluating 5 + 4 × 23?

A. k, t, u
B. n, s, q
C. m, k, r
D. m, p, l
Answer: k, t, u
Explanation:
The correct order of operations when evaluating 5 + 4 × 23 is Add 5 and 4, Multiply 9 and 2 and Evaluate 18³
Thus the correct answer is option A.
Question 12.
The ratio of scrambled eggs to hard-boiled eggs served at a restaurant is 6 : 2.
Part A Make a ratio table showing three possible combinations of
Part B Represent the ratio relationship using a graph.
Part C Use the graph to find the number of hard-boiled eggs served when the restaurant serves 15 scrambled eggs.
Answer:
Part A – The three possible combinations are
3 : 1
12 : 4
18 : 6
Part B –
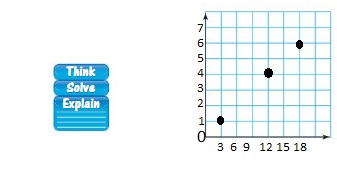
Part C-
The ratio is 3:1
The ratio for 15 scrambled eggs
15 :5
Conclusion:
You can Download Middle School Big Ideas Math Answers Grade 6 Chapter 3 Ratios and Rates through the direct links provided here. Make use of the links and practice well for the exams. Keep in touch with our site to get the latest updates regarding the BIM 6th Grade Answer Key Chapter wise.