Get free step by step solutions to Big Ideas Math Answers Grade 6 Chapter 5 Algebraic Expressions and Properties here. The topics covered in Algebraic Expressions and Properties chapter are Algebraic Expressions, Writing Expressions, Properties of Addition and Multiplication, and so on. We have provided solutions for all the problems in an easy manner. Learn the properties with examples on this page. This Big Ideas Math Answers Grade 6 Chapter 5 Algebraic Expressions and Properties will help you to enhance your performance in math.
Big Ideas Math Book 6th Grade Answer Key Chapter 5 Algebraic Expressions and Properties
Quick and simple learning is possible only with our Big Ideas Math Book 6th Grade Solution Key Chapter 5 Algebraic Expressions and Properties. The concepts of Algebraic Expressions and Properties are well explained by the math experts. We have provided the solutions as per the list of the topics. Just tap the links and start practicing the problems for the exams and score well.
Algebraic Expressions and Properties STEAM Video/Performance
Lesson: 1 Algebraic Expressions
Lesson: 2 Writing Expressions
Lesson: 3 Properties of Addition and Multiplication
- Lesson 5.3 Properties of Addition and Multiplication
- Properties of Addition and Multiplication Homework & Practice 5.3
Lesson: 4 The Distributive Property
Lesson: 5 Factoring Expressions
Chapter: 5 – Algebraic Expressions and Properties
- Algebraic Expressions and Properties Connecting Concepts
- Algebraic Expressions and Properties Chapter Review
- Algebraic Expressions and Properties Practice Test
- Algebraic Expressions and Properties Cumulative Practice
Algebraic Expressions and Properties STEAM Video/Performance
Shadow Drawings
Expressions can be used to represent the growth of living things over time. Can you think of any other real-life situations in which you would want to use an expression to represent a changing quantity?
Watch the STEAM Video “Shadow Drawings.” Then answer the following questions.
Question 1.
Tory traces the shadow of a plant each week on the same day of the week and at the same time of day. Why does she need to be so careful about the timing of the drawing?
Answer:
Tory traces the shadow of a plant each week on the same day of the week and at the same time of day.
Because she needs to represent the growth of the plant over time. Thus she needs to be very careful about the timing of the drawing.
Question 2.
The table shows the height of the plant each week for the first three weeks. About how tall was the plant after 1.5 weeks? Explain your reasoning.
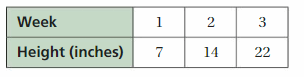
Answer: 10.5 inches
Explanation:
The above table represents the height of the plant for 3 weeks.
1 week = 7 inches
0.5 week = 7/2 = 3.5 inches
1.5 week = 7 + 3.5 = 10.5 inches
Question 3.
Predict the height of the plant when Tory makes her next three weekly drawings.
Answer: 42 inches (approx)
Explanation:
The height of the plant is increased by 7 inches every week.
The height of the plant is increased to 22 inches for the first three weeks.
7 × 6 = 42 inches
Thus we predict the height of the plant when Tory makes her next three weekly drawings is 42 inches.
Performance Task
Describing Change
After completing this chapter, you will be able to use the concepts you learned to answer the questions in the STEAM Video Performance Task. You will be given data sets for the following real-life situations.

You will be asked to use given data to write expressions and make predictions. Do the expressions provide accurate predictions far into the future?

Getting Ready for Chapter 5
Question 1.
Work with a partner.
a. You baby sit for 3 hours. You receive $24. What is your hourly wage?
- Write the problem. Underline the important numbers and units you need to solve the problem.
- Read the problem carefully a second time. Circle the key phrase for the question.

- Write each important number or phrase, with its units, on a piece of paper. Write +, −, ×, ÷, and = on five other pieces of paper.

- Arrange the pieces of paper to answer the question, “What is your hourly wage?”
- Evaluate the expression that represents the hourly wage.
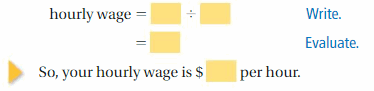
Answer:
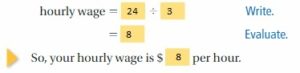
According to the given details, Babysit receives $24 for 3 hours.
3 hours = $24
1 hour = 24/3 = $8
Thus your hourly wage is $8
b. How can you use your hourly wage to find how much you will receive for any number of hours worked?
Answer:
You can multiply by $8 in given any number of hours worked to get the total receive.
Vocabulary
The following vocabulary terms are defined in this chapter. Think about what each term might mean and record your thoughts.

Lesson 5.1 Algebraic Expressions
EXPLORATION 1

Work with a partner. Identify any missing information that is needed to answer each question. Then choose a reasonable quantity and write an expression for each problem. After you have written the expression, evaluate it using mental math or some other method.

a. You receive $24 for washing cars. How much do you earn per hour?
Answer:
Let the number of hours 8.
24 ÷ 8 = 3
Thus you earn $3 per hour.
b. You buy 5 silicone baking molds at a craft store. How much do you spend?

Answer:
Let the cost of each silicone baking molds is $3
5 × $3 = $15
Thus you spend $15 to buy 5 silicone baking molds.
c. You are running in a mud race. How much farther do you have to go after running 2000 feet?

Answer:
You are running a 4500-foot race.
4500 – 2000 = 2500 feet
Thus you have to run 2500 feet more.
d. A rattlesnake is 25 centimeters long when it hatches. The snake grows at a rate of about 1.6 centimeters per month for several months. What is the length of the rattlesnake?

Answer:
Given,
A rattlesnake is 25 centimeters long when it hatches. The snake grows at a rate of about 1.6 centimeters per month for several months.
Let the number of months be m
25 + 1.6m
If months = 12
1.6 × 12 = 19.2 cms
25 + 19.2 = 44.2 centimeters
5.1 Lesson

An algebraic expression is an expression that may contain numbers, operations, and one or more variables. A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
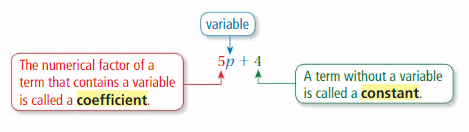
Try It
Identify the terms, coefficients, and constants in the expression.
Question 1.
12 + 10c
Answer:
12 – constant
10 – coefficient
c – variable or term
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 2.
15 + 3w + \(\frac{1}{2}\)
Answer:
15 and \(\frac{1}{2}\) – constant
3 – coefficient
w – variable or term
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 3.
z2 + 9z
Answer:
2 – exponent
9 – coefficient
z – variable or term
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
write the expression using exponents.
Question 4.
j . j . j . j . j . j
Answer:
j raised to the sixth power
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Question 5.
9 . k . k . k . k . k
Answer:
9 – constant
k raised to the fifth power
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Question 6.
Evaluate 24 + c when c = 9.
Answer: 33
Explanation:
Given equation
24 + c
and also given c is equal to 9
substitute c value in the equation we get
24 + 9 = 33
Question 7.
Evaluate d − 17 when d = 30.
Answer: 13
Explanation:
Given equation
d – 17
and also given d is equal to 30
substitute d value in the equation we get
30 – 17 = 13
Question 8.
Evaluate 18 ÷ q when q = \(\frac{1}{2}\)
Answer: 36
Explanation:
Given equation
18 ÷ q
and also given q is equal to \(\frac{1}{2}\)
substitute q value in the equation we get
18 ÷ \(\frac{1}{2}\) = 36
Evaluate the expression when p = 24 and q = 8.
Question 9.
p ÷ q
Answer:
p = 24
q = 8
p ÷ q
Substitute the value of p and q in the expression
24 ÷ 8 = 3
Question 10.
q + p
Answer: 32
Explanation:
Given,
p = 24
q = 8
q + p
Substitute the value of p and q in the expression
8 + 24 = 32
Hence we get the answer is 32
Question 11.
p – q
Answer: 16
Explanation:
Given,
p = 24
q = 8
p – q
Substitute the value of p and q in the expression
24 – 8 = 16
Hence we get the answer is 16
Question 12.
p . q
Answer: 192
Explanation:
Given,
p = 24
q = 8
p . q
Substitute the value of p and q in the expression
24 . 8 by multiplying 24 with 8 we get 192
Hence the answer is 192
Evaluate the expression when y = 6.
Question 13.
5y + 1
Answer: 31
Explanation:
Given equation
5y + 1
and also given y = 6
Now substitute 6 in the given equation
5.6 + 1 is
5 multiply with 6 and then add with 1 we get 30 + 1 is 31
hence answer is 31
Question 14.
30 – 24 ÷ y
Answer: 1
Explanation:
Given equation
30 – 24 ÷ y
and also given y = 6
Now substitute 6 in the given equation
30 – 24 ÷ y is
30 – 24 ÷6
6 ÷ 6
six divided by six
we get 1
Hence answer is 1
Question 15.
y2 – 7
Answer: 29
Explanation:
Given equation
y² – 7
and also given y = 6
Now substitute 6 in the given equation
y2 – 7
6² – 7
6 × 6 – 7
36 – 7
29
Hence answer is 29
Question 16.
1.5 + y2
Answer: 37.5
Explanation:
Given equation
1.5 + y²
and also given y = 6
Now substitute 6 in the given equation
1.5 + 6²
1.5 +36
37.5
Hence answer is 37.5
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 17.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.

Answer: The expression 3(4) + 5 does not belong to the other three. Because it does not contain any variable in the expression.
Question 18.
ALGEBRAIC EXPRESSIONS
Identify the terms, coefficients, and constants in the expression 9h + 1.
Answer:
1 – constant
9 – coefficient
h – variable or term
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
EVALUATING EXPRESSIONS
Evaluate the expression when m = 8.
Question 19.
m – 7
Answer: 1
Given equation
m – 7
given m value is 8
Now substitute m value 8 in the given equation we get
m – 7
8 – 7
1
Hence the answer is 1
Question 20.
5m + 4
Answer: 44
Given equation
5m + 4
given m value is 8
Now substitute m value 8 in the given equation we get
5 . 8 + 4
40 + 4
44
Hence the answer is 44
Question 21.
NUMBER SENSE
Does the value of the expression 20 − x increase, decrease, or stay the same as x increases? Explain.
Answer:
When the value of x increases, the value of 20 – x decreases. And when the value of x does not change, 20 – x remains the same. When greater values of x are subtracted from 20, you will have a lower value left. Therefore, as x increases, the value of the expression 20 – x will decrease.
Question 22.
OPEN-ENDED
Write an algebraic expression using more than one operation. When you evaluate the expression, how do you know which operation to perform first?
Answer:
Example 40 – 2(6 – 4)²
40 – 2 (2)²
40 – 2(4)
40 – 8
32
When evaluating an expression, proceed in this order:
parentheses are done first.
exponents are done next.
multiplication and division are done as they are encountered from left to right.
addition and subtraction are done as they are encountered from left to right.
Question 23.
STRUCTURE
Is the expression 8.2 ÷ m . m . m . m the same as the expression 8.2 ÷ m4? Explain your reasoning.
Answer: Yes
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Hence the expression 8.2 ÷ m . m . m . m the same as the expression 8.2 ÷ m⁴
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 24.
The expression 12.25m + 29.99 gives the cost (in dollars) of a gym membership for m months. You have $180 to spend on a membership. Can you buy a one-year membership?
Answer: Yes.
Given
The expression 12.25m + 29.99
gym membership for m months
You have $180 to spend on a membership
Let’s solve your equation step-by-step.
12.25m+29.99=180
Step 1: Subtract 29.99 from both sides.
12.25m+29.99−29.99=180−29.99
12.25m=150.01
Step 2: Divide both sides by 12.25.
12.25m/12.25=150.01/12.25
m=12.245714
The expression 12.25m + 29.99= 12.25(12.24)+29.99 = 179.93
Question 25.
DIG DEEPER!
The expression p −15 gives the amount (in dollars) you pay after using the coupon when the original amount of a purchase is p dollars. The expression 30 + 6n gives the amount of money (in dollars) you save after n weeks. A jacket costs $78. Can you buy the jacket after 6 weeks? Explain.

Answer:
The amount you pay using coupon = p (purchase) -15
so we simply plug in our value into this equation
$78- $15 = $63
so $63 is the amount you pay after using the coupon on an original purchase of $78
n = 6 weeks
30 + 6n
30 + 6(6)
30 + 36 = 66
No, you cannot buy the jacket after 6 weeks.
Algebraic Expressions Homework & Practice 5.1
Review & Refresh
You ask 40 students which of three items from the cafeteria they like the best. You record the results on the piece of paper shown.

Question 1.
What percent of students answered salad?
Answer: 25%
Explanation:
Total number of students = 40
The number of students who like a salad in the Cafeteria food is 10 students
40/10 = 4
The percentage of the students is
(10/40) × 100 = 25%
Thus the percentage of students who answered salad is 25%.
Question 2.
How many students answered pizza?
Answer: 12 students
Explanation:
Total number of students = 40
The number of students who like a salad in the Cafeteria food is 10 students
The number of students who answered pasta is 18
40 – 18 – 10 = 12
Thus the number of students who answered pizza is 12.
Question 3.
What percent of students answered pasta?
Answer: 45%
Explanation:
Total number of students = 40
The number of students who answered pasta is 18
(18/40) × 100 = 45
Thus the percentage of students who answered pasta is 45%
Find the missing quantity in the double number line.
Question 4.
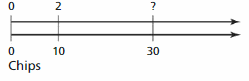
Answer:
The ratio of 2 and 10 is 1:5
The equivalent ratio of 1:5 is 6:30
So, the missing quantity is 6.
Question 5.
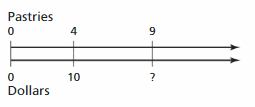
Answer:
Based on the ratios we can find the missing quantity.
The cost of 1 pastry is $2.5
The cost of 9 pastries is $22.5

Divide. Write the answer in simplest form.
Question 6.
1\(\frac{3}{8}\) ÷ \(\frac{3}{4}\)
Answer: \(\frac{1}{2}\)
To simplify a fraction, divide the top and bottom by the highest number that
can divide into both numbers exactly.
Simplifying (or reducing) fractions means making the fraction as simple as possible
Question 7.
2\(\frac{7}{9}\) ÷ 2
Answer: \(\frac{7}{9}\)
To simplify a fraction, divide the top and bottom by the highest number that
can divide into both numbers exactly.
Simplifying (or reducing) fractions means making the fraction as simple as possible
Question 8.
4 ÷ 4\(\frac{2}{5}\)
Answer: \(\frac{5}{2}\)
To simplify a fraction, divide the top and bottom by the highest number that
can divide into both numbers exactly.
Simplifying (or reducing) fractions means making the fraction as simple as possible
Question 9.
3\(\frac{2}{3}\) ÷ 1\(\frac{2}{7}\)
Answer: latex]\frac{14}{3}[/latex]
To simplify a fraction, divide the top and bottom by the highest number that
can divide into both numbers exactly.
Simplifying (or reducing) fractions means making the fraction as simple as possible
Concepts, Skills, & Problem Solving
EVALUATING EXPRESSIONS
Write and evaluate an expression for the problem. (See Exploration 1, p. 201.)
Question 10.
The scores on your first two history tests are 82 and 95. By how many points did you improve on your second test?
Answer: 13
Explanation:
The scores on your first two history tests are 82 and 95.
95 – 82 = 13
Thus you have to improve 13 points on your second test.
Question 11.
You buy a hat for $12 and give the cashier a $20 bill. How much change do you receive?
Answer: $8
Explanation:
Given,
You buy a hat for $12 and give the cashier a $20 bill.
20 – 12 = 8
Thus you receive $8 change.
Question 12.
You receive $8 for raking leaves for 2 hours. What is your hourly wage?
Answer: $4
Explanation:
Given,
You receive $8 for raking leaves for 2 hours.
2 hour = $8
1 hour = ?
8/2 = 4
Thus the hourly wage is $4.
Question 13.
Music lessons cost $20 per week. How much do 6 weeks of lessons cost?
Answer: $120
Explanation:
Given,
Music lessons cost $20 per week.
1 week = $20
$20 × 6 = $120
Thus the cost of 6 weeks is $120.
ALGEBRAIC EXPRESSIONS
Identify the terms, coefficients, and constants in the expression.
Question 14.
7h + 3
Answer:
3 – constant
7 – coefficient
h – variable or term
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 15.
g + 12 + 9g
Answer:
12 – constant
9 – coefficient
g – variable or term
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 16.
5c2 + 7d
Answer:
2 – exponent
5 and 7 – coefficient
c and d – variable or term
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 17.
2m2 + 15 + 2p2
Answer:
15 – constant
2 – exponent
2 – coefficient
m and p – variable or term
A term without a variable is called a constant.
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 18.
6 + n2 + \(\frac{1}{2}\)d
Answer:
6 – constant
\(\frac{1}{2}\)– exponent
2 – coefficient
n and d – variable or term
A term without a variable is called a constant.
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 19.
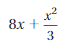
Answer:
2 – exponent
8 and \(\frac{1}{3}\)– coefficient
x – variable or term
A term without a variable is called a constant.
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 20.
YOU BE THE TEACHER
Your friend finds the terms, coefficients, and constants in the algebraic expression 2x2y. Is your friend correct? Explain your reasoning.

Answer:

A term without a variable is called a constant.
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 21.
PERIMETER
You can use the expression 2ℓ + 2w to find the perimeter of a rectangle, where ℓ is the length and w is the width.
a. Identify the terms, coefficients, and constants in the expression.

Answer:
Given Expression 2ℓ + 2w
The coefficients of the expression are 2.
terms – l, w
b. Interpret the coefficients of the terms.
Answer: The coefficients of the terms are 2, 2
2 + 2 = 4
USING EXPONENTS
Write the expression using exponents.
Question 22.
b . b . b
Answer:
b raised to the third power
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Question 23.
g . g . g . g . g
Answer:
g raised to the fifth power
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Question 24.
8 . w . w . w . w
Answer:
8 – constant
w raised to the fourth power
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Question 25.
5 . 2 . y . y . y
Answer:
5 and 2 – constant
y raised to the third power
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Question 26.
a . a . c . c
Answer:
a and c raised to the two power
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Question 27.
2 . 1 . x . z . z .z . z
Answer:
2 and 1 – constant
x raised to the 1 power
z raised to the fourth power
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Question 28.
YOU BE THE TEACHER
Your friend writes the product using exponents. Is your friend correct? Explain your reasoning.

Answer: correct
5 – constant
n raised to the fourth power
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
Question 29.
AREA
Write an expression using exponents that represents the area of the square.

Answer:
Side = 5d
Area of the square = s × s
A = 5d × 5d
A = 25d²
Question 30.
REASONING
Suppose the man in the St. Ives poem has x wives, each wife has x sacks, each sack has x cats, and each cat has x kits. Write an expression using exponents that represent the total number of kits, cats, sacks, and wives.

Answer:
Suppose the man in the St. Ives poem has x wives, each wife has x sacks, each sack has x cats, and each cat has x kits.
x = 7
7 × 7 × 7 × 7
EVALUATING EXPRESSIONS
Evaluate the expression when a = 3, b = 2, and c = 12.
Question 31.
6 + a
Answer: 9
Explanation:
Given equation
6 + a
given data
a = 3
now substitute given data in the equation we get
6 + 3 = 9
hence the answer is 9
Question 32.
b.5
Answer: 10
Explanation:
Given equation
b.5
given data
b = 2
now substitute given data in the equation we get
2 . 5= 10 (2 multiply by 5)
hence the answer is 10
Question 33.
c – 1
Answer: 11
Explanation:
Given equation
c – 1
given data
c = 12
now substitute given data in the equation we get
12 – 1 = 11
hence the answer is 11
Question 34.
27 ÷ a
Answer: 9
Explanation:
Given equation
27 ÷a
given data
a = 3
now substitute given data in the equation we get
27 ÷ 3 = 9
Hence the answer is 9
Question 35.
12 – b
Answer: 10
Explanation:
Given equation
12 -b
given data
b = 2
now substitute given data in the equation we get
12 – 2 = 10
Hence the answer is 10
Question 36.
c + 5
Answer: 17
Explanation:
Given equation
c + 5
given data
c = 12
now substitute given data in the equation we get
12+ 5 = 17
Hence the answer is 17
Question 37.
2a
Answer: 6
Explanation:
Given equation
2a
given data
a = 3
now substitute given data in the equation we get
2(3) = 6
Hence the answer is 6
Question 38.
c ÷ 6
Answer: 2
Explanation:
Given equation
c ÷ 6
given data
c = 12
now substitute given data in the equation we get
12 ÷ 6 = 2
Hence the answer is 2
Question 39.
a + b
Answer: 5
Explanation:
Given equation
a + b
given data
a = 3, b = 2
now substitute given data in equation we get
3 + 2 = 5
hence the answer is 5
Question 40.
c + a
Answer: 15
Explanation:
Given equation
a + b
given data
a = 3, b = 2
now substitute given data in equation we get
3 + 2 = 5
hence the answer is 5
Question 41.
c – a
Answer: 11
Explanation:
Given equation
c – a
given data
a = 3, c = 12
now substitute given data in equation we get
12 – 3 = 11
hence the answer is 11
Question 42.
a – b
Answer: 1
Explanation:
Given equation
a – b
given data
a = 3, b = 2
now substitute given data in equation we get
3 – 2 = 1
hence the answer is 1
Question 43.
\(\frac{c}{a}\)
Answer: 4
Explanation:
Given equation
\(\frac{c}{a}\)
given data
a = 3, c = 12
now substitute given data in equation we get
\(\frac{12}{3}\) = 4
hence the answer is 4
Question 44.
\(\frac{c}{b}\)
Answer: 6
Explanation:
Given equation
\(\frac{c}{b}\)
given data
b = 2, c = 12
now substitute given data in equation we get
\(\frac{12}{2}\) = 6
hence the answer is 6
Question 45.
b.c
Answer: 24
Explanation:
Given equation
b . a
given data
b = 2, c = 12
now substitute given data in equation we get
2(12) = 24
hence the answer is 24
Question 46.
c(a)
Answer: 36
Explanation:
Given equation
c(a)
given data
a = 3, c = 12
now substitute given data in equation we get
12(3) = 36
hence the answer is 36
Question 47.
PROBLEM SOLVING
You earn 15n dollars for mowing n lawns. How much do you earn for mowing 1 lawn? 7 lawns?
Answer:
Given,
You earn 15n dollars for mowing n lawns.
n = 1
15 × 1 = 15
n = 7
15 × 7 = 105
Thus you earn $15 for mowing 1 lawn and $105 for mowing 7 lawns.
EVALUATING EXPRESSIONS
Copy and complete the table.
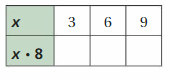
Question 48.
Answer:
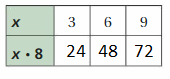
Explanation:
Given data from the table
x = 3 ,6, and 9
substitute x values in the given equation x . 8
3(8) = 24
6(8) = 48
9(8) = 72
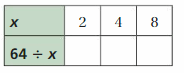
Question 49.
Answer:
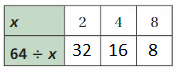
Explanation:
Given data from the table
x = 2 ,4, and 8
substitute x values in the given equation 64 ÷ x = 24
64 ÷ 2 = 32
64 ÷ 4 = 16
64 ÷ 8 = 8
Question 50.
MODELING REAL LIFE
Due to gravity, an object falls 16t2 feet in t seconds. You drop a rock from a bridge that is 75 feet above the water. Will the rock hit the water in 2 seconds? Explain.
Answer: No
Given
Due to gravity, an object falls 16t2 feet in t seconds. You drop a rock from a bridge that is 75 feet above the water
d = 16t² (d in ft, t in sec)
Set d = 75 ft and solve for t.
75 = 16t²
t = √(75/16) sec ≅ 2.17 sec
It hits the water in 2.17 sec.
EVALUATING EXPRESSIONS
Evaluate the expression when a = 10, b = 9, and c = 4.
Question 51.
2a + 3
Answer: 23
Given equation
2a + 3
given data
a = 10,
now substitute given data in equation we get
2(10)+3
= 20 + 3
= 23
hence the answer is 23
Question 52.
4c – 7.8
Answer:
Given equation
4c – 7.8
given data
a = 10,
now substitute given data in equation we get
4(4) – 7.8
= 16 – 7.8
= 8.2
Hence the answer is 8.2
Question 53.
\(\frac{a}{4}\) + \(\frac{1}{3}\)
Answer: \(\frac{17}{6}\) or 2.83
Given equation
\(\frac{a}{4}\) + \(\frac{1}{3}\)
given data
a = 10,
now substitute given data in equation we get
\(\frac{10}{4}\) + \(\frac{1}{3}\)
= \(\frac{17}{6}\)
= 2.83
hence the answer is \(\frac{17}{6}\) or 2.83
Question 54.
\(\frac{24}{b}\) + 8
Answer:
\(\frac{32}{3}\) or 10.66
Given equation
\(\frac{24}{b}\) + 8
given data
b = 9,
now substitute given data in equation we get
\(\frac{24}{9}\) + 8
= \(\frac{8}{3}\) + 8
= \(\frac{32}{3}\)
= 10.66
Hence the answer is \(\frac{32}{3}\) or 10.66
Question 55.
c2 + 6
Answer: 22
Given equation
c² + 6
given data
c = 4,
now substitute given data in equation we get
c² + 6
= 4² + 6
= (4 × 4) + 6
= 16 + 6
= 22
Hence the answer is 22
Question 56.
a2 – 18
Answer: 82
Given equation
a² – 18
given data
a = 10,
now substitute given data in equation we get
a² – 18
= 10² – 18
= (10 × 10) – 18
= 100 – 18
= 82
Hence the answer is 82
Question 57.
a + 9c
Answer: 40
Given equation
a + 9c
given data
a = 10, c = 4
now substitute given data in equation we get
10 + 9(4)
= 10 + 36
= 46
Hence the answer is 46
Question 58.
bc + 12.3
Answer: 48.3
bc + 12.3
given data
b = 9, c = 4
now substitute given data in equation we get
9(4) + 12.3
= 36 + 12.3
= 48.3
Hence the answer is 48.3
Question 59.
3a + 2b – 6c
Answer: 24
3a + 2b – 6c
given data
a = 10, b = 9, c = 4
now substitute given data in equation we get
3(10) + 2(9) – 6(4)
= 30 + 18 – 24
= 24
Hence the answer is 24
Question 60.
YOU BE THE TEACHER
Your friend evaluates the expression when m = 8. Is your friend correct? Explain your reasoning.
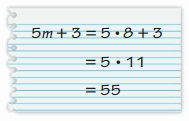
Answer: incorrect.
Explanation:
Given the expression 5m + 3
m = 8
5 × 8 + 3
40 + 3 = 43
By this we can say that your friend is incorrect.
Question 61.
PROBLEM SOLVING
After m months, the height of a plant is (10 + 3m) millimeters. How tall is the plant after 8 months? 3 years?
Answer:
8 months = 34 millimeters
EXPLANATION:
You have to plug in the number 8 as “m” in the equation then solve. 10 + 3(8)
3 years = 118 millimeters
3 years converted to months would be 12×3 which equals 36. Then put it into the equation 10 + 3(36) and you do the multiplication first.
Question 62.
STRUCTURE
You use a video streaming service to rent x new releases and y standard rentals. Which expression tells you how much money you will need?
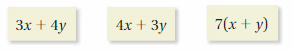

Answer:
4x+3y
Explanation:
It is given that,
The number of new releases are represented by ‘x’ and number of standard rentals are represented by ‘y’.
Also, the cost for one new release = $4 and the cost of one standard rental = $3.
Thus, the cost of ‘x’ new releases = $4x and the cost of ‘y’ new releases = $3y.
So, the total cost = cost of ‘x’ new releases + cost of ‘y’ standard rentals.
i.e. Total cost = 4x + 3y in dollars.
Thus, the expression to tell the money required is 4x+3y.
Question 63.
OPEN-ENDED
You float 2000 feet along a lazy river water ride. The ride takes less than 10 minutes. Give two examples of possible times and speeds.
Answer:
if you travel at 200 feet per minute you can make in ten minutes
Question 64.
DIG DEEPER!
The expression 20a + 13c is the cost (in dollars) for a adults and c students to enter a science center.
a. How much does it cost for an adult? a student? Explain your reasoning.
Answer:
It costs $20 per adult. If this is a cost function,
which it is because the wording is “the cost (in dollars) for adults and c students”, the adult is the cost for 1 adult, 1a, is 20.
That relates the number of adults to the cost of 1 adult.
It costs $13 per student. Again, this is a cost function, so since the student is c,
the cost for 1 student, 1c, is 13. That relates the number of students to the cost of 1 student.
b. Find the total cost for 4 adults and 24 students.
Answer:
The total cost for 4 adult and 24 students looks like this:
20(4) + 13(24) which is 80 + 312 = $392
c. You find the cost for a group. Then the numbers of adults and students in the group both double. Does the cost double? Explain your answer using an example.
Answer:
If you have 3 adults and 3 students in your group, the cost is 20(3) + 13(3) which is $99.
If you double the number of each, let’s see if the cost doubles.
We will “up” the numbers to 6 each. 20(6) + 13(6) = $198. Is $198 the double of $99.
Yes it is. Let’s do it again to check. Let’s double the 6.
20(12) + 13(12) = $396, and $198 doubled does in fact equal $396
d. In part(b), the number of adults is cut in half, but the number of students doubles. Is the cost the same? Explain your answer.
Answer:
20(12) + 13(12) = $396, and $198 doubled does in fact equal $396.
Question 65.
REASONING
The volume of the cube (in cubic inches) is equal to four times the area of one of its faces (in square inches). What is the volume of the cube?
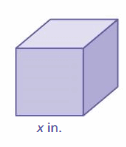
Answer:
Given,
The volume of the cube (in cubic inches) is equal to four times the area of one of its faces (in square inches).
We know that,
The volume of a cube = x³
Multiply 3 sides = x × x × x = x³
Lesson 5.2 Writing Expressions
EXPLORATION 1
Writing Expressions
Work with a partner. You use a $20 bill to buy lunch at a café. You order a sandwich from the menu board shown.

a. Complete the table. In the last column, write a numerical expression for the amount of change you receive.
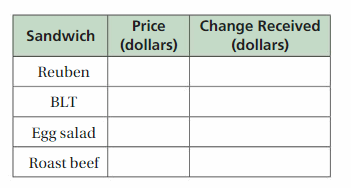
Answer:
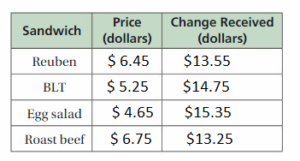
b. Write an algebraic expression that represents the amount of change you receive when you order any sandwich from the menu board.
Answer:
You have only $20 for lunch, so if you order any sandwich from the menu
the board then the amount will be change
if you ordered chicken salad then your changing amount is
price = $ 4.95
change Received = $20 – $4.95 = $15.05
change Received = $15.05
c. The expression 20 − 4.65 represents the amount of change one customer receives after ordering from the menu board. Explain what each part of the expression represents. Do you know what the customer ordered? Explain your reasoning.

Answer:
calculated changing amount for chicken salad in part (b),
so comparison between chicken salad expression and beef expression
For Chicken salad
Price = $4.95
change Recived = $20 – $4.95 = $15.05
change Recieved = $15.05
For Roast Beef
price = $6.75
Change Recived = $20 – $6.75 = $13.25
change Recived = $13.25
5.2 Lesson
Some words can imply math operations.

Try It
Write the phrase as an expression.
Question 1.
the sum of 18 and 35
Answer: 53
Given
the sum of 18 and 35
so by add 18 with 35
we get 18+35
=53
So the answer is 53
Question 2.
6 times 50
Answer: 300
given
6 times 50
so multiply 6 with 50 we get
300
Hence the answer is 300
Write the phrase as an expression.
Question 3.
25 less than a number b
Answer: b – 25
Question 4.
a number x divided by 4
Answer: \(\frac{x}{4}\)
Question 5.
the total of a number t and 11
Answer: t + 11
Question 6.
100 decreased by a number k.
Answer: 100 – k
Try It
Question 7.
Your friend has 5 more than twice as many game tokens as you. Let t be the number of game tokens you have. Write an expression for the number of game tokens your friend has.
Answer: 5+2t
given
Your friend has 5 more than twice as many game tokens as you
5+2t because 5 more then is adding 5 and twice as many is doubling or multiplying by 2
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
WRITING EXPRESSIONS
Write the phrase as an expression.
Question 8.
the sum of 7 and 11
Answer: 7 + 11 we get 18
Question 9.
5 subtracted from 9
Answer: 9 – 5 we get 4
Question 10.
DIFFERENT WORDS, SAME QUESTION
Which is different? Write “both” expressions.

Answer: 12 more than x and x increased by 12 has different words but the question is same.
Question 11.
PRECISION
Your friend says that the phrases below have the same meaning. Is your friend correct? Explain your reasoning.
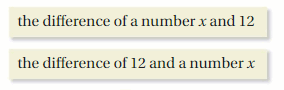
Answer: No your friend is incorrect.
“the difference of number x and 12” is x – 12
“the diffrence of 12 and number x” is 12 – x
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
A company rents paddleboards by charging a rental fee plus an hourly rate. Write an expression that represents the cost (in dollars) of renting a paddleboard for h hours. How much does an eight-hour rental cost?

Answer:
The independent variable is that whose values do not take into account the values of other variables.
That is the time in hours for this item. Then, for the dependent variable, the answer would be the cost of renting.
The value of the dependent variable is based on the changes done in the values of the independent variable.
Question 13.
DIG DEEPER!
A county fair charges an entry fee of $7 and $0.75 for each ride token. You have $15. Write an expression that represents the amount (in dollars) you have left after entering the fair and purchasing n tokens. How many tokens can you purchase? How much money do you have left after purchasing 6 tokens?

Answer:
Given,
A county fair charges an entry fee of $7 and $0.75 for each ride token.
You have $15.
15.00 – 7.00 = 8.00
6 x .75 = 4.50
8.00- 4.5 = 3.50
Writing Expressions Homework & Practice 5.2
Review & Refresh
Identify the terms, coefficients, and constants in the expression.
Question 1.
4f + 8
Answer:
8 – constant
4 – coefficient
f- variable or term
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 2.
\(\frac{4}{5}\) + 3s + 2
Answer:
\(\frac{4}{5}\) and 2 – constant
3 – coefficient
s- variable or term
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 3.
9h2 + \(\frac{8}{9}\)p + 1
Answer:
1 – constant
2 – exponent
9 and \(\frac{8}{9}\) – coefficient
h and p – variable or term
An exponent is a number or letter written above and to the right of a mathematical expression called the base
The exponent tells us how many times the base is used as a factor
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Copy and complete the statement.
Question 4.
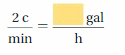
Answer: 7.5 gallon per hour
Explanation:
Convert from cup per minute to gallon per hour
1 Cup per minute = 3.75 gallon per hour
2 cup per minute = 2 × 3.75 = 7.5 gallon per hour
Question 5.
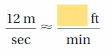
Answer: 2362.2 feet per minute
Explanation:
Convert from meter per second to feet per minute
1 meter per second = 196.85 feet per minute
12 minute per second = 2362.2 feet per minute
Question 6.
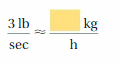
Answer: 4898.79 kg per hour
Explanation:
Convert from lb per second to kg per hour
1 lb per second = 1632.93 kg per hour
3 lb per second = 4898.79 kg per hour
Divide. Write the answer in simplest form.
Question 7.
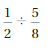
Answer: \(\frac{8}{9}\) or 0.533
Explanation:
by dividing \(\frac{1}{2}\) with \(\frac{5}{8}\)
we get \(\frac{1}{2}\) ÷ \(\frac{5}{8}\)
\(\frac{8}{9}\)
0.533
Question 8.
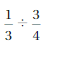
Answer: \(\frac{4}{9}\)
Explanation:
by dividing \(\frac{1}{3}\) with \(\frac{3}{4}\)
we get \(\frac{1}{3}\) ÷ \(\frac{3}{4}\)
\(\frac{4}{9}\)
0.44
Question 9.
![]()
Answer: \(\frac{2}{15}\) or 0.133
Explanation:
by dividing \(\frac{2}{5}\) with \(\frac{3}{1}\)
we get \(\frac{2}{5}\) ÷ \(\frac{3}{1}\)
\(\frac{2}{15}\)
0.133
Question 10.
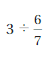
Answer: \(\frac{7}{2}\) or 3.5
Explanation:
by dividing \(\frac{3}{1}\) with \(\frac{6}{7}\)
we get \(\frac{3}{1}\) ÷ \(\frac{6}{7}\)
\(\frac{7}{2}\)
3.5
Concepts, Skills, & Problem Solving
STRUCTURE
The expression represents the amount of change you receive after buying n sandwiches. Explain what each part of the expression represents. (See Exploration 1, p. 209.)
Question 11.
10 – 5.25n
Answer:
Let us assume that you buy 1 sandwich.
10 – 5.25(1)
= 10 – 5.25
= 4.75
Question 12.
20 – 4.95n
Answer:
Let us assume that you buy 2 sandwiches.
20 – 4.95(2)
20 – 9.9 = 10.1
Question 3.
100 – 6.75n
Answer:
Let us assume that you buy 6 sandwiches.
100 – 6.75(6)
= 100 – 40.50
= 59.50
WRITING EXPRESSIONS
Write the phrase as an expression.
Question 14.
5 less than 8
Answer: 5 < 8
Explanation:
The phrase “less than” indicates < symbol.
So, the expression is 5 < 8
Question 15.
the product of 3 and 12
Answer: 3 × 12
Explanation:
The phrase “product” indicates multiplication.
So, the expression is 3 × 12
Question 16.
28 divided by 7
Answer: 28 ÷ 7
Explanation:
The phrase “divided by” indicates ÷ symbol
So, the expression is 28 ÷ 7
Question 17.
the total of 6 and 10
Answer: 6 + 10 = 16
Explanation:
The phrase “total” indicates ‘+’ symbol.
So, the expression is 6 + 10 = 16
Question 18.
3 fewer than 18
Answer: 18 – 3
Explanation:
The phrase fewer than indicates ‘subtraction’
So, the expression is 18 – 3
Question 19.
17 added to 15
Answer: 17 + 15
Explanation:
Given 17 added to 15
so add 17 with 15
Question 20.
13 subtracted from a number x
Answer: 13 – x
Explanation:
The number represents the variable x
So here we have to subtract number x from 13
That gives the expression 13 – x
Question 21.
5 times a number d
Answer: 5d
Explanation:
The number represents variable d.
The word “times” represents ×
So the expression is 5d
Question 22.
the quotient of 18 and a number a
Answer: 18 ÷ a
Explanation:
a represents the number
So, the expression would be 18 ÷ a
Question 23.
the difference of a number s and 6
Answer: s – 6
Question 24.
7 increased by a number w
Answer: 7 + w
Question 25.
a number t cubed
Answer: t³
YOU BE THE TEACHER
Your friend writes the phrase as an expression. Is your friend correct? Explain your reasoning.
Question 26.

Answer: incorrect
Explanation:
Given,
The quotient of 8 and a number is y is 8 ÷ y
By this, we can say that your friend is incorrect.
Question 27.
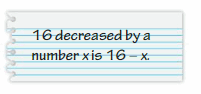
Answer: correct
Explanation:
Given,
16 decreased by a number x
It means we have to subtract x from 16.
Thus the expression is 16 – x.
Question 28.
NUMBER SENSE
Five friends share the cost of a dinner equally.
a. Write an expression that represents the cost (in dollars) per person.
Answer: 600 ÷ p
b. Make up a reasonable total cost and test your expression.
Answer:
The total cost of dinner is $600.
Now divide the cost per person.
There are 5 friends.
The expression is 600 ÷ p
p = 5
600 ÷ 5 = 12
The cost per person is $120
Question 29.
MODELING REAL LIFE
A biologist analyzes 15 bacteria samples each day.
a. Copy and complete the table.
b. Write an expression that represents the total number of samples analyzed after n days.
Answer:
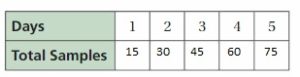
The expression that represents the total number of samples analyzed after n days is 15n
Question 30.
PROBLEM SOLVING
To rent a moving truck for the day, it costs $33 plus $1 for each mile driven.
a. Write an expression that represents the cost (in dollars) to rent the truck.
Answer: 33 + d
b. You drive the truck 300 miles. How much do you pay?
Answer:
Use the expression 33 + d to find how much do you pay.
33 + 300 = 333
Thus you pay $333 for 300 miles.
WRITING PHRASES
Give two ways to write the expression as a phrase.
Question 31.
n + 6
Answer:
According to the given details, we can write the expression in two ways
a number n more than 6
the sum of a number n and 6
Question 32.
4w
Answer:
According to the given details, we can write the expression in two ways
a number w is four times
The product of 4 and a number w
Question 33.
15 – b
Answer:
According to the given details we can write the expression in two ways.
15 decreased by a number d
The difference of 15 and a number b
Question 34.
14 – 3z
Answer:
According to the given details, we can write the expression in two ways.
The product of 3 and z subtracted from 14.
The difference of 14 and product of 3 and a number z.
EVALUATING EXPRESSIONS
Write the phrase as an expression. Then evaluate the expression when x = 5 and y = 20.
Question 35.
3 less than the quotient of a number y and 4
Answer:
given 3 less than the quotient of a number y and 4
The quotient of a number y and 4
Now we are given that 3 less than the quotient of a number y and 4
So, \(\frac{y}{4}\) – 3
Hence the expression becomes \(\frac{y}{4}\) – 3
Question 36.
the sum of a number x and 4, all divided by 3
Answer:
given
a sum, x and 4, so that becomes x + 4
All divided by denotes that we need to do the addition before division, so we need to put it in parentheses:
(x + 4)
And it is divided by 3.
So you can write the answer down in a few different ways:
(x + 4) ÷ 3
(x + 4) / 3
\(\frac{x + 4}{3}\)
Question 37.
6 more than the product of 8 and a number x
Answer:
A Product is an answer to a multiplication.
The product of 8 and a number is 8×n=8n
6 more than that means to add on 6
So the expression “6 more than the product of 8 and a number” is
8n+6
Question 38.
the quotient of 40 and the difference of a number y and 16
Answer:
as we know that
The expression ” the quotient of and the difference of a number y and ” is equivalent to the algebraic equation
\(\frac{40}{y-16}\)
For y = 20 given problem
substitute the value of y in the equation
\(\frac{40}{20-16}\) = \(\frac{40}{4}\) = 10
Question 39.
MODELING REAL LIFE
It costs $3 to bowl a game and $2 for shoe rental.
a. Write an expression that represents the total cost (in dollars) of g games.
b. Use your expression to find the total cost of 8 games.

Answer:
a. If shoes are for all games in row, P=2+3g
b. If not, P=5g, with g the number of games
Explanation:
The price depends if shoes are included for the whole games, you just have to pay them once and then you have to pay g games, so P(g)=2+3g
Else, you have to pay for g shoes and g bowl party, so P(g)=2g+3g⇔P(g)=5g
Question 40.
MODELING REAL LIFE
Florida has 8 less than 5 times the number of counties in Arizona. Georgia has 25 more than twice the number of counties in Florida.
a. Write an expression that represents the number of counties in Florida.
b. Write an expression that represents the number of counties in Georgia.
c. Arizona has 15 counties. How many do Florida and Georgia have?
Answer:
Number of countries in Florida=5×a-8
Number of countries in Georgia=2×f+25
Explanation:
Given that the number of countries in Florida is denoted by f,
The number of countries in Arizona is given by a and the number of countries in Georgia is given by g.
as Florida has 8 less than five times the number of countries in Arizona
So f=5×a-8
Georgia has 25 more than twice the number of countries in Florida
So g=2×f+25
Now it is given that Arizona has 15 countries i.e. a=15
So f=5×15-8
f=67
g=2×67+25
g=159
Hence, the number of countries in Florida is:67
number of countries in Georgia is:159
Question 41.
PATTERNS
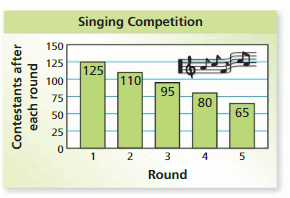
There are 140 people in a singing competition. The graph shows the results for the first five rounds.
a. Write an expression that represents the number of people after each round.
b. Assuming this pattern continues, how many people compete in the ninth round? Explain your reasoning.
Answer:
a) The expression is y = 140 – 15 x
b ) There are 5 participants in the 9th round
Step-by-step explanation:
Step 1 :
From the graph we can see that,
Number of people in the singing competition = 140
Number of people in the first round = 125
Number of people in the second round = 110
Number of people in the third round = 95
Number of people in the fourth round = 80
Number of people in the fifth round = 65
Step 2 :
From the given data, We can get that the difference between the number of people participating in each round is 15 less than the previous round .
The first round has 15 people less than the total number of 140
Let x represent the number of the round and y represent the number of people participating in each round .
Then the expression to represent this would be
y = 140 – 15 x
Step 3 :
To find the number of participants in the 9th round given the same pattern continues.
For the 9th round x = 9, as x represents the number of the round
Substituting this in the equation obtained in step 2, we get
y = 140 -15 (9) = 140 – 135 = 5
There are 5 participants in the 9th round
Question 42.
NUMBER SENSE
The difference between two numbers is 8. The lesser number is a. Write an expression that represents the greater number.
Answer:
Given The difference between the two numbers is 8. The lesser number is a.
b-a=8
b is the greater number; b>a
So, b=a+8
Question 43.
NUMBER SENSE
One number is four times another. The greater number is x. Write an expression that represents the lesser number
Answer: y = x/4
Let us assume the smaller number y.
We know that four times the smaller number is equal to x. So, four times y is equal to x.
Turning this into an expression, you get 4y = x.
This means, to get y on its own, we need to divide by 4 on both sides, giving us the answer of y = x/4
Lesson 5.3 Properties of Addition and Multiplication
EXPLORATION 1
Identifying Equivalent Expressions
Work with a partner.
a. Choose four values for a variable x. Then evaluate each expression for each value of x. Are any of the expressions equivalent? Explain your reasoning.
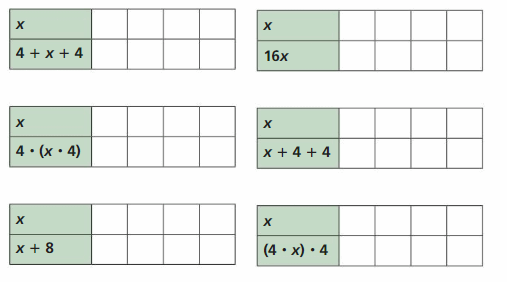
Answer:
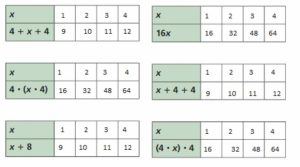
The equation x + 8, 4 + 4 + x, x + 4 + 4 are equal.
The equation 16x, 4.(x.4), (4.x).x are equal.
b. You have used the following properties in a previous course. Use the examples to explain the meaning of each property.


Are these properties true for algebraic expressions? Explain your reasoning.
Answer:
Commutative property of addition: The commutative property of addition says that changing the order of addends does not change the sum. Here’s an example: 5 + 2 = 7 or 2 + 5 = 7
Commutative property of multiplication: The commutative property of multiplication tells us that we can multiply a string of numbers in any order. Basically: 2 x 3 x 5 will create the same answer as 3 x 5 x 2, or 2 x 5 x 3
Associative property of addition: The associative property of addition says that changing the grouping of the addends does not change the sum.
Example: 2 + (7 + 5) = (2 + 7) + 5
Associative Property of Multiplication: The associative property is a math rule that says that the way in which factors are grouped in a multiplication problem does not change the product.
Example: 2 × (7 × 5) = (2 × 7) × 5
5.3 Lesson
Expressions that result in the same number for any value of each variable are equivalent expressions. You can use the Commutative and Associative Properties to write equivalent expressions.

Try It
Simplify the expression. Explain each step.
Question 1.
10 + (a + 9)
Answer: a+19
Step 1: Eliminate redundant parentheses
10+(a+9)=10+a+9
Step 2:Add the numbers
Step 3: Rearrange terms
a+19
Question 2.
(c + \(\frac{2}{3}\)) + \(\frac{1}{2}\)
Answer: c + \(\frac{7}{6}\)
(c + \(\frac{2}{3}\)) + \(\frac{1}{2}\)
c+ \(\frac{7}{6}\)
Question 3.
5(4n)
Answer: 20n
Multiply 5 with 4n
we get 20n
Simplify the expression. Explain each step.
Question 4.
12.b.0
Answer: 0
step 1
12 multiply with a number b
and then multiply with 0
we get 0
Question 5.
1.m.24
Answer: 24m
step 1
1 multiply with a number m
and then multiply with 24
we get 24m
Question 6.
(t + 15) + 0
Answer: t + 15
step 1
Add t + 15 with 0
and then
we get t + 15
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
USING PROPERTIES
Simplify the expression. Explain each step.
Question 7.
(7 + c) + 4
Answer:
Step 1: Eliminate redundant parentheses
4+(7+c)= 4+7+c
Step 2:Add the numbers
Step 3: Rearrange terms
11 + c
Question 8.
4(b.6)
Answer: 24b
Step 1: Eliminate redundant parentheses
4 × b× 6 = 4 × 6× b
multiply 4 with 6 we get 24 and then with b
so we get 24b
Question 9.
0.b.9
Answer: 0
Step 1: Eliminate redundant parentheses
0 × b× 9 = 0 × 9× b
multiply 0 with 9 we get 0 and then with b
so we get 0
Question 10.
WRITING
Explain what it means for expressions to be equivalent. Then give an example of equivalent expressions.
Answer:
equivalent expressions are algebraic expressions that, although they look different, turn out to really be the same.
Example:
Let’s consider this algebraic expression: 2(x^2 + x). If we substitute 1 for the variable, the expression equals 4. But what about the expression
2x^2 + 2x? If, again, we substitute 1 for the variable x, we still get 4. How does this happen?
What we really did was simplify the original expression by distributing the 2 into the part in parentheses. So we really haven’t changed the expression at all – all we’ve done is rewrite it in a different form.
Because these two expressions are really the same, no matter what number we substitute for x, the results will always be identical. If we use 0, both expressions come out to 0. If we use 10, both expressions come out to 220. If we use 100, both expressions come out to 20,200. We get the same result no matter how large or small the number we use for x.
Question 11.
OPEN-ENDED
Write an algebraic expression that can be simplified using the Associative Property of Multiplication and the Multiplication Property of One.
Answer:
Let us consider an expression 4 × 30.
We can simplify the expression by using the Associative Property of Multiplication
4 × 30 = 4 × (5 × 6)
(4 × 5) × 6 = 4 × (5 × 6)
20 × 6 = 4 × 30
120 = 120
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 12.
You and five friends form a team for an outdoor adventure race. Your team needs to raise money to pay for $130 of travel fees, x dollars for each team member’s entry fee, and $85.50 for food. Use an algebraic expression to find the total amount your team needs to raise when the entry fee is $25.50 per person.

Answer: (130+85)+25.5p=total amount
Step-by-step explanation:
130+85 is how much you’d need just for the fees and food, for the entry fee its per person
so it would be $25.5 for every person that is part of your team.
Question 13.
You have $50 and a $15 gift card to spend online. You purchase a pair of headphones for $34.99 and 8 songs for x dollars each. Use an algebraic expression to find the amount you have left when each song costs $1.10.
Answer: $21.21
Given
You have $50 and a $15 gift card to spend online
purchase a pair of headphones for $34.99 and 8 songs for x dollars each.
Use an algebraic expression to find the amount you have left when each song costs $1.10.
so
50 + 15 -34.99 – 8x
65 – 34.99 – 8(1.10)
30.01 – 8.8
$21.21
Properties of Addition and Multiplication Homework & Practice 5.3
Review & Refresh
Write the phrase as an expression.
Question 1.
10 added to a number p
Answer: p + 10
First consider the expression for
10 added to a number p
we get p + 10
An algebraic expression is a mathematical phrase that contains a combination of numbers, variables and operational symbols.
A variable is a letter that can represent one or more numbers.
Question 2.
the product of 6 and a number m
Answer: 6m
First consider the expression for
the product of 6 and a number m
so multiply 6 with m
we get 6m
An algebraic expression is a mathematical phrase that contains a combination of numbers, variables and operational symbols.
A variable is a letter that can represent one or more numbers.
Question 3.
the quotient of a number b and 15
Answer: \(\frac{b}{15}\)
First consider the expression for
the quotient of a number b and 15
so divide b by 15
we get \(\frac{b}{15}\)
An algebraic expression is a mathematical phrase that contains a combination of numbers, variables and operational symbols.
A variable is a letter that can represent one or more numbers.
Question 4.
7 fewer than a number s
Answer: s – 7
First consider the expression for
7 fewer than a number s
so subtract a number s with 7
we get s – 7
An algebraic expression is a mathematical phrase that contains a combination of numbers, variables and operational symbols.
A variable is a letter that can represent one or more numbers.
Write the prime factorization of the number.
Question 5.
36
Answer:
The number 36 can be written as a product of primes as
36 = 2² x 3².
The expression 2² x 3² is said to be the prime factorization of 36
Question 6.
144
Answer:
The prime factor of the 144 is 24 x 32.
144 = 2 x 2 x 2 x 2 x 3 x 3
Question 7.
147
Answer:
Factors of 147: 1, 3, 7, 21, 49, 147.
Prime factorization: 147 = 3 x 7 x 7,
which can also be written
147 = 3 x (7²)
Question 8.
205
Answer:
the prime factors of the number 205.
If we put all of it together we have the factors 5 x 41 = 205.
it can also be written in exponential form as 5¹ x 41¹.
Evaluate the expression.
Question 9.
8.092 + 3.5
Answer: 11.592
Given expression 8.092 + 3.5
now add 8.092 with 3.5 we get
11.592
Question 10.
16.78 – 12.237
Answer: 4.543
Given expression 16.78 – 12.237
now subtract 16.75 with 12.237 we get
4.543
Question 11.
9.17 + 1.83 + 2.641
Answer: 13.641
Given expression 9.17 + 1.83 + 2.641
now add 9.17 with 1.83 we get 11 then add with 2.641
we get 13.641
Question 12.
8.43 – 6.218 + 4.2
Answer:
Given expression 8.43 – 6.218 + 4.2
now subtract 8.43 with 6.218 we get 2.212 then add with 4.2
we get 6.412
Represent the ratio relationship using a graph.
Question 13.
Answer:
Question 14.
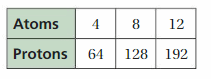
Answer:
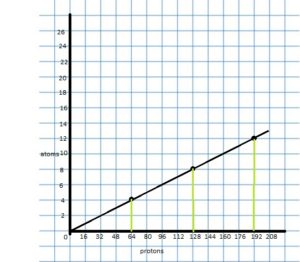
Concepts, Skills, & Problem Solving
MATCHING
Match the expression with an equivalent expression. (See Exploration 1, p. 215.)
Question 15.
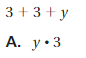
Answer: B
Explanation:
3 + 3 + y is equivalent to y + 3 + 3
So, the correct answer is option B
Question 16.
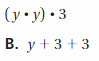
Answer: C
Explanation:
(y.y).3 = y(3 . y)
So, the correct answer is option C.
Question 17.
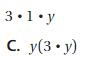
Answer: A
Explanation:
3 . 1 . y = y . 3
So, the correct answer is option A.
Question 18.
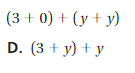
Answer: D
Explanation:
(3 + 0) + (y + y)
(3 + y) + y
So, the correct answer is option D.
IDENTIFYING PROPERTIES
Tell which property the statement illustrates.
Question 19.
![]()
Answer: commutative property of multiplication
Explanation:
The commutative property of multiplication tells us that we can multiply a string of numbers in any order.
5 . p = p . 5
Question 20.
2 + (12 + r) = (2 + 12) + r
Answer: associative property of addition
Explanation:
Associative property of addition: Changing the grouping of addends does not change the sum.
2 + (12 + r) = (2 + 12) + r
Question 21.
4 . (x . 10) = (4 . x) . 10
Answer: associative property of multiplication
Explanation:
The associative property is a math rule that says that the way in which factors are grouped in a multiplication problem does not change the product.
Question 22.
x + 7.5 = 7.5 + x
Answer: commutative property of addition
Explanation:
The commutative property of addition says that changing the order of addends does not change the sum.
Question 23.
(c + 2) + 0 = c + 2
Answer: Additive Identity
Explanation:
Additive identity is a number, which when added to any number, gives the sum as the number itself. It means that additive identity is “0” as adding 0 to any number, gives the sum as the number itself.
Question 24.
a . 1 = a
Answer: Multiplicative Identity
Explanation:
According to the multiplicative identity property of 1, any number multiplied by 1, gives the same result as the number itself. It is also called the Identity property of multiplication because the identity of the number remains the same.
Question 25.
YOU BE THE TEACHER
Your friend states the property that the statement illustrates. Is your friend correct? Explain your reasoning.
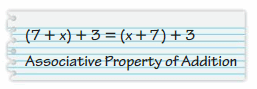
Answer: correct
Explanation:
Associative property of addition: Changing the grouping of addends does not change the sum.
(7 + x) + 3 = (x + 7) + 3
Thus we can say that your friend is correct.
USING PROPERTIES
Simplify the expression. Explain each step.
Question 26.
6 + (5 + x)
Answer: 11 + x
Step 1: Eliminate redundant parentheses
6 + (5 + x) = 6+5+x
Step 2:Add the numbers
Step 3: Rearrange terms
11 + x
Question 27.
(14 + y) + 3
Answer: 17 + y
Step 1: Eliminate redundant parentheses
(14 + y) + 3 = 14 + 3 + y
Step 2:Add the numbers
Step 3: Rearrange terms
17 + y
Question 28.
6(2b)
Answer: 12b
Step 1: Eliminate redundant parentheses
6(2b) = 6 × 2 ×b
Step 2:multiply the numbers
Step 3: Rearrange terms
we get 12b
Question 29.
7(9w)
Answer: 63w
Step 1: Eliminate redundant parentheses
7(9w) = 7 × ×w
Step 2:multiply the numbers
Step 3: Rearrange terms
we get 63w
Question 30.
3.2 + (x + 5.1)
Answer: 8.3 + x
Step 1: Eliminate redundant parentheses
3.2 + (x + 5.1) = 3.2 + 5.1 + x
Step 2:Add the numbers
Step 3: Rearrange terms
8.3 + x
Question 31.
(0 + a) + 8
Answer: 8 + a
Step 1: Eliminate redundant parentheses
(0 + a) + 8 = 0 + 8 +a
Step 2:Add the numbers
Step 3: Rearrange terms
8 + a
Question 32.
9 . c . 4
Answer: 36c
Step 1: Eliminate redundant parentheses
9 . c . 4 = 9 . 4 . c
Step 2: multiply the numbers
Step 3: Rearrange terms
36c
Question 33.
(18.6 . d) . 1
Answer: 18.6 d
Step 1: Eliminate redundant parentheses
(18.6 . d) . 1 = (18.6 . 1) d
Step 2: multiply the numbers
Step 3: Rearrange terms
18.6 d
Question 34.
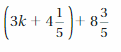
Answer:
Step 1: Eliminate redundant parentheses
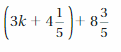 = 3k + (4\(\frac{1}{5}\) + 8\(\frac{3}{5}\))
= 3k + (4\(\frac{1}{5}\) + 8\(\frac{3}{5}\))
Step 2: add the numbers
Step 3: Rearrange terms
3k + 12\(\frac{4}{5}\)
Question 35.
(2.4 + 4n) + 9
Answer:
Step 1: Eliminate redundant parentheses
(2.4 + 4n) + 9 = 2.4 + 9 + 4n
Step 2:Add the numbers
Step 3: Rearrange terms
11.4 + 4n
Question 36.
(3s) . 8
Answer: 24s
Step 1: Eliminate redundant parentheses
(3s) . 8 = (3 . 8) s
Step 2: multiply the numbers
Step 3: Rearrange terms
24s
Question 37.
z . 0 . 12
Answer: 0
Step 1: Eliminate redundant parentheses
z . 0 . 12 = z × 0 × 12
Step 2: multiply the numbers
Step 3: Rearrange terms
0
Question 38.
GEOMETRY
The expression 12 + x + 4 represents the perimeter of a triangle. Simplify the expression.
Answer: x+16
Explanation:
your simplifying so you only combine like terms.
12 and 4 dont have any variables following them so you add the two.
12+4=16
there is only 1 x in the expression so just add it on.
16+x
Question 39.
PRECISION
A case of scout cookies has 10 cartons. A carton has 12 boxes. The amount you earn on a whole case is 10(12x) dollars.
a. What does x represent?
b. Simplify the expression.
Answer:
Given
A case of scout cookies has 10 cartons. A carton has 12 boxes
A. x represents the money made per box
B. 10(12x) = 120x
Question 40.
MODELING REAL LIFE
A government estimates the cost to design new radar technology over a period of m months. The government estimates $840,000 for equipment, $15,000 for software,and $40,000 per month for wages. Use an algebraic expression to find the total cost the government estimates when the project takes 16 months to complete.

Answer: $1,495,000.
Explanation:
The cost that is affected by the number of months mm is the wages while the first two costs are fixed. Hence, you multiply $40,000 by the number of months so that
840,000+15,000+40,000m
840,000+15,000+40,000m
For m=16m=16 (16 months),
=840,000+15,000+40,000(16)
=840,000+15,000+40,000(16)
=840,000+15,000+640,000
=840,000+15,000+640,000
=1,495,000
=1,495,000
So, the total cost is $1,495,000.
WRITING EXPRESSIONS
Write the phrase as an expression. Then simplify the expression.
Question 41.
7 plus the sum of a number x and 5
Answer:
7+(x+5) sum means addition and it says x and 5. then it says 7 plus that so you put 7.
In reality, you wouldn’t need parenthesis,
but if you want it to match the phrase, you can put it in parenthesis.
Question 42.
the product of 8 and a number y, multiplied by 9
Answer: 8y x 9 ⇒ 72y
Given
the product of 8 and a number y ⇒ 8 × y = 8y
and also given multiplied by 9 ⇒ 8y × 9
so we get 72 y
USING PROPERTIES
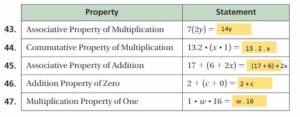
Copy and complete the statement using the specified property.
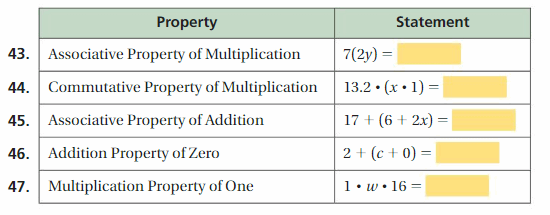
Answer:
Question 48.
GEOMETRY
Five identical triangles form the trapezoid shown.
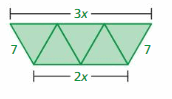
a. What is the perimeter of the trapezoid?
Answer:
The perimeter of the trapezoid is a + b + c + d
P = sum of four sides
P = 3x + 7 + 7 + 2x
P = 5x + 14
Thus the perimeter of the trapezoid is 5x + 14
b. How can you use some or all of the triangles to form a new trapezoid with a perimeter of 3x +14? Explain your reasoning.
Answer:
You can reduce the size of the triangle to form a new trapezoid with a perimeter of 3x +14
The perimeter of the trapezoid is a + b + c + d
P = sum of four sides
P = 2x + 7 + 7 + 1x
P = 3x + 14
Question 49.
DIG DEEPER!
You and a friend sell hats at a fair booth. You sell 16 hats on the first shift and 21 hats on the third shift. Your friend sells x hats on the second shift.
a. The expression 37(14) + 10x represents the amount (in dollars) that you both earn. How can you tell that your friend is selling the hats for a lower price?
b. You earn more money than your friend. What can you say about the value of x?
Answer:
37+x
Explanation:
1st shift: 16 hats were sold
2nd shift: x hats were sold
3rd shift: 21 hats were sold
The total is
16+x+21
Simplifying
37+x
another step
16 + 21 + x = y
y = the number of hats sold
16 = hats sold on first shift
21 = hats on the third shift
x = hats on the second shift
Lesson 5.4 The Distributive Property
EXPLORATION 1
Using Models to Simplify Expressions
Work with a partner.
a. Use the models to simplify the expressions. Explain your reasoning.
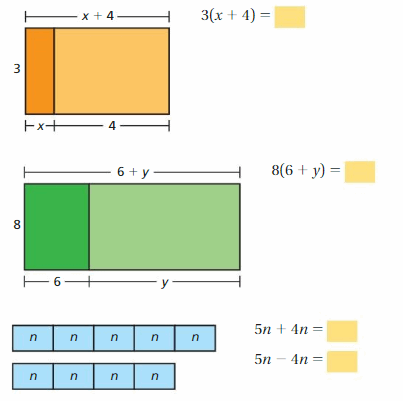
Answer:
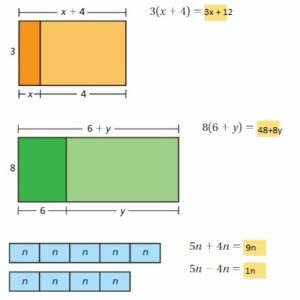
b. In part(a), check that the original expressions are equivalent to the simplified expressions.
c. You used the Distributive Property in a previous course. Use the example to explain the meaning of the property.

Distributive Property: 6(20 + 3) = 6(20) + 6(3)
Is this property true for algebraic expressions? Explain your reasoning.
Answer:
The distributive property of multiplication over addition can be used when you multiply a number by a sum.
6(20 + 3) = 6(20) + 6(3)
6(23) = 120 + 18
138 = 138
Yes this property true for algebraic expressions
Try It
Use the Distributive Property to simplify the expression.
Question 1.
7(a + 2)
Answer: 7(a) + 7(2)
Explanation:
Given,
The distributive property of multiplication over addition can be used when you multiply a number by a sum.
7(a + 2) = (7 × a) + (7 × 2)
7a + 14
Thus 7(a + 2) = 7a + 14
Question 2.
3(d – 11)
Answer: 3(d) – 3(11)
Explanation:
Given,
The distributive property of multiplication over addition can be used when you multiply a number by a sum.
3(d – 11) = (3 × d) – (3 × 11)
3d – 33
Thus 3(d – 11) = 3d – 33
Question 3.
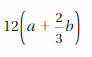
Answer: 12a + 12\(\frac{2}{3}\)b
Explanation:
Given,
The distributive property of multiplication over addition can be used when you multiply a number by a sum.
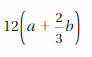 = (12 × a) + (12 × \(\frac{2}{3}\)b)
= (12 × a) + (12 × \(\frac{2}{3}\)b)
= 12a + 12\(\frac{2}{3}\)b
Thus 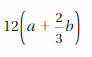 = 12a + 12\(\frac{2}{3}\)b
= 12a + 12\(\frac{2}{3}\)b
Question 4.
7(2 + 6 – 4d)
Answer: 7(2) + 7(6) – 7(4d)
Explanation:
Given,
The distributive property of multiplication over addition can be used when you multiply a number by a sum.
7(2 + 6 – 4d) = 7(8 – 4d)
56 – 28d
Thus 7(2 + 6 – 4d) = 56 – 28d
Simplify the expression.
Question 5.
8 + 3z – z
Answer: 8 + 2z
Explanation:
Combine the like terms and simplify the expression.
8 + 3z – z
8 + z(3 – 1)
8 + 2z
So, 8 + 3z – z = 8 + 2z
Question 6.
3(b + 5) + b + 2
Answer: 4b + 17
Explanation:
Combine the like terms and simplify the expression.
3(b + 5) + b + 2
= 3b + 15 + b + 2
= 3b + b + 15 + 2
= 4b + 17
Thus 3(b + 5) + b + 2 = 4b + 17
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 7.
WRITING
One meaning of the word distribute is to give something to each member of a group. How can this help you remember the Distributive Property?
Answer:
You must distribute or give the number outside the parenthesis to all the numbers inside the parenthesis
SIMPLIFYING EXPRESSIONS
Use the Distributive Property to simplify the expression.
Question 8.
3(x + 10)
Answer: 3(x) + 3(10)
Explanation:
We can simplify the expression by using the Distributive Property
The distributive property of multiplication over addition can be used when you multiply a number by a sum.
3(x + 10) = (3 × x) + (3 × 10)
= 3x + 30
So, 3(x + 10) = 3x + 30
Question 9.
15(4n – 2)
Answer: 15(4n) – 15(2)
Explanation:
We can simplify the expression by using the Distributive Property
The distributive property of multiplication over addition can be used when you multiply a number by a sum.
15(4n – 2) = (15 × 4n) – (15 × 2)
= 60n – 30
So, 15(4n – 2) = 60n – 30
Question 10.
2w + 4 + 13w + 1
Answer:15w + 5 = 5(3w + 1)
Explanation:
We can simplify the expression by using the Distributive Property
The distributive property of multiplication over addition can be used when you multiply a number by a sum.
2w + 4 + 13w + 1
Combine the like terms
=2w + 13w + 4 + 1
=15w + 5
=5(3w + 1)
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 11.
You purchase a remote-controlled drone for d dollars. Your friend purchases a drone that costs $35 more than your drone. Your brother purchases a drone that costs three times as much as your friend’s drone. Write and simplify an expression that represents the cost (in dollars) of your brother’s drone.
Answer:
Brother = 105+3d
Explanation:
Given
Drone = d
Friend = $35 more expensive than yours.
Brother = 3 times as much as your friend
Required
Write an expression for the cost of your brother’s drone
I’ll solve by analyzing the question one sentence after the other
You: Drone = d
Your friend:
Friend = $35 more expensive than yours.
This means
Brother = 3 × Friend
Substitute 35 + d for Friend
Brother = 3 × (35+d)
Open bracket
Brother = 3×35+3×d
Brother=105+3d
Question 12.
Write and simplify an expression that represents the total cost (in dollars) of buying the items shown for each member of a baseball team.

Answer: 9(10 + x)
Explanation:
Number of members in the baseball team = 9
Cost of the pant = $10
Cost of a belt = $x
The expression that represents the total cost (in dollars) of buying the items shown for each member of a baseball team is 9(10 + x)
Question 13.
DIG DEEPER!
One molecule of caffeine contains x oxygen atoms, twice as many nitrogen atoms as oxygen atoms, 4 more carbon atoms than nitrogen atoms, and 1.25 times as many hydrogen atoms as carbon atoms. Write and simplify an expression that represents the number of hydrogen atoms in one molecule of caffeine.
Answer:
Given,
One molecule of caffeine contains x oxygen atoms, twice as many nitrogen atoms as oxygen atoms, 4 more carbon atoms than nitrogen atoms, and 1.25 times as many hydrogen atoms as carbon atoms.
One molecule of caffeine contains x oxygen atoms = x
twice as many nitrogen atoms as oxygen atoms = 2 . x
4 more carbon atoms than nitrogen atoms = 4 . x
1.25 times as many hydrogen atoms as carbon atoms = 1.25 × x
x + 2x + 6x + 1.25(6x)
The Distributive Property Homework & Practice 5.4
Review & Refresh
Simplify the expression. Explain each step.
Question 1.
(s + 4) + 8
Answer: s + 12
Explanation:
According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.
(s + 4) + 8
= s + 4 + 8
= s + 12
Question 2.
(12 + x) + 2
Answer: 14 + x
Explanation:
According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.
12 + x + 2
x + 12 + 2
x + 14
Question 3.
3(4n)
Answer: 12n
Explanation:
According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.
3 × 4n = 12n
You are given the difference of the numbers of boys and girls in a class and the ratio of boys to girls. How many boys and how many girls are in the class?
Question 4.
3 more boys; 5 for every 4
Answer:
Let the total number of boys in the class be x.
The ratio of boys and girls is 5 : 4
Number of boys = 5x
Number of girls = 4x
5x – 4x = 3
x = 3
Number of boys = 5(3) = 15
15 + 3 = 18
Number of girls = 4(3) = 12
To find the total number of boys and girls in the class we have to add them
18 + 12 = 30
Thus there are 30 boys and girls in the class.
Question 5.
8 more girls; 3 for every 2
Answer:
Let the total number of boys in the class be x.
The ratio of boys and girls is 3 : 2
Number of boys = 3x
Number of girls = 2x
3x – 2x = 8
x = 8
Number of boys = 3x = 3(8) = 24
Number of girls = 2x = 2(8) = 16
More number of girls = 16 + 8 = 24
To find the total number of boys and girls in the class we have to add them
24 + 24 = 48
Thus there are 48 boys and girls in the class.
Question 6.
4 more girls; 9 for every 13
Answer:
Let the total number of boys in the class be x.
The ratio of girls and boys is 13 : 9
Number of boys = 9x
Number of girls = 13x
13x – 9x = 4
4x = 4
x = 1
Number of boys = 9x = 9(1) = 9
Number of girls = 13x = 13(1) = 13
13 + 4 = 17
To find the total number of boys and girls in the class we have to add them
9 + 17 = 26
Thus there are 26 boys and girls in the class.
Question 7.
6 more boys; 7 for every 4
Answer:
Let the total number of boys in the class be x.
The ratio of girls and boys is 7 : 4
Number of boys = 7x
Number of girls = 4x
7x – 4x = 6
3x = 6
x = 2
Number of boys = 7(2) = 14
Number of girls = 4(2) = 8
15 + 6 = 21
To find the total number of boys and girls in the class we have to add them
21 + 8 = 29
Thus there are 29 boys and girls in the class.
Divide.
Question 8.
301 ÷ 7
Answer: 43
So divide 301 with 7
then we get 43
Question 9.
1722 ÷ 14
Answer: 123
So divide 1722 with 14
then we get 123
Question 10.
629 ÷ 12
Answer: 52.41
So divide 629 with 12
then we get 52.14
Question 11.
8068 ÷ 31
Answer: 260.25
So divide 8068 with 31
then we get 260.25
Concepts, Skills, & Problem Solving
USING MODELS
Use the model to simplify the expression. Explain your reasoning. (See Exploration 1, p. 221.)
Question 12.
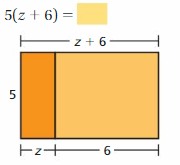
Answer: 5z + 30
Explanation:
The shape of the above figure is a rectangle.
Area of the rectangle = l × b
A = (z + 6) × 5
A = 5z + 30
Question 13.
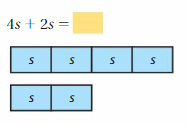
Answer: 6s
Explanation:
Combine the like terms
There are 4s in the first block
There are 2s in the second block
4s + 2s = 6s
SIMPLIFYING EXPRESSIONS
Use the Distributive Property to simplify the expression.
Question 14.
3(x + 4)
Answer: 3x + 12
Explanation:
We can use the distributive property to simplify the expression.
3(x + 4) = (3 × x) + (3 × 4)
= 3x + 12
Question 15.
10(b – 6)
Answer: 10b – 60
Explanation:
We can use the distributive property to simplify the expression.
10(b – 6) = (10 × b) – (10 × 6)
= 10b – 60
Question 16.
6(s – 9)
Answer: 6s – 54
Explanation:
We can use the distributive property to simplify the expression.
6(s – 9) = (6 × s) – (6 × 9)
= 6s – 54
Question 17.
7(8 + y )
Answer: 56 + 7y
Explanation:
We can use the distributive property to simplify the expression.
7(8 + y) = (7 × 8) + (7 × y)
= 56 + 7y
Question 18.
8(12 + a)
Answer: 96 + 8a
Explanation:
We can use the distributive property to simplify the expression.
8(12 + a) = (8 × 12) + (8 × a)
= 96 + 8a
Question 19.
9(2n + 1)
Answer: 18n + 9
Explanation:
We can use the distributive property to simplify the expression.
9(2n + 1) = (9 × 2n) + (9 × 1)
= 18n + 9
Question 20.
12(6 – k)
Answer: 72 – 12k
Explanation:
We can use the distributive property to simplify the expression.
12(6 – k) = (12 × 6) – (12 × k)
= 72 – 12k
Question 21.
18(5 – 3w)
Answer: 90 – 54w
Explanation:
We can use the distributive property to simplify the expression.
18(5 – 3w) = (18 × 5) – (18 × 3w)
= 90 – 54w
Question 22.
9(3 + c + 4)
Answer: 63 + 9c
Explanation:
We can use the distributive property to simplify the expression.
9(3 + c + 4) = 9(7 + c)
(9 × 7) + ( 9 × c)
63 + 9c
Question 23.
![]()
Answer: 3 + x/4
Explanation:
We can use the distributive property to simplify the expression.
1/4(8 + x + 4) = 1/4(12 + x)
= 3 + x/4
Question 24.
8(5g + 5 – 2)
Answer: 40g + 24
Explanation:
We can use the distributive property to simplify the expression.
8(5g + 5 – 2) = 8(5g) + 8(5) – 8(2)
40g + 40 – 16
40g + 24
Question 25.
6(10 + z + 3)
Answer: 78 + 6z
Explanation:
We can use the distributive property to simplify the expression.
6(10 + z + 3) = 6(10) + 6(z) + 6(3)
= 60 + 6z + 18
= 78 + 6z
Question 26.
4(x + y)
Answer: 4x + 4y
Explanation:
We can use the distributive property to simplify the expression.
4(x + y) = (4 × x) + (4 × y)
= 4x + 4y
Question 27.
25(x – y)
Answer: 25x – 25y
Explanation:
We can use the distributive property to simplify the expression.
25(x – y) = (25 × x) – (25 × y)
= 25x – 25y
Question 28.
7(p + q + 9)
Answer: 7p + 7q + 63
Explanation:
We can use the distributive property to simplify the expression.
7(p + q + 9) = (7 × p) + (7 × q) + (7 × 9)
= 7p + 7q + 63
Question 29.
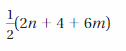
Answer: n + 3m + 2
Explanation:
We can use the distributive property to simplify the expression.
1/2 (2n + 4 + 6m) = 1/2 (2n) + 1/2 (4) + 1/2 (6m)
= n + 2 + 3m
MATCHING
Match the expression with an equivalent expression.
Question 30.
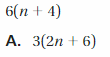
Answer: C
Explanation:
Given,
6(n + 4) = 6n + 24
Now take 3 as common factor
3(2n + 8)
Thus the equivalent expression is option C.
Question 31.
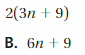
Answer: A
Explanation:
Given,
2(3n + 9) = 6n + 18
Now take 3 as common factor
6n + 18 = 3(2n + 6)
Thus the equivalent expression is option A.
Question 32.
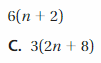
Answer: D
Explanation:
Given,
6(n + 2) = 6n + 12
Thus the equivalent expression is option D.
Question 33.
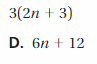
Answer: B
Explanation:
Given,
3(2n + 3) = 6n + 9
Thus the equivalent expression is option B.
Question 34.
STRUCTURE
Each day, you run on a treadmill for r minutes and lift weights for 15 minutes. Which expressions can you use to find how many minutes of exercise you do in 5 days? Explain your reasoning.
![]()
Answer: 5(r + 15)
Explanation:
Each day, you run on a treadmill for r minutes and lift weights for 15 minutes.
They are both expressions with r as the variable.
They are not equivalent expressions.
They are equivalent expressions.
Both expressions contain the terms 5, r, and 15.
5(15 + r) = 5(15) + 5(r)
Question 35.
MODELING REAL LIFE
A cheetah can run 103 feet per second. A zebra can run x feet per second. Write and simplify an expression that represents how many feet farther the cheetah can run in 10 seconds.

Answer:
Given,
A cheetah can run 103 feet per second. A zebra can run x feet per second.
We are given that the rate of cheetah Rc is:
Rc = 103 ft / sec
And the rate of zebra Rz is:
Rz = x ft / sec
We are to find the distance between the two after 10 seconds, that is:
distance = (103 – x) 10
distance = 1030 – 10 x
COMBINING LIKE TERMS
Simplify the expression.
Question 36.
6(x + 4) + 1
Answer: 6x + 25
Explanation:
Given the expression
6(x + 4) + 1
= (6 × x) + (6 × 4) + 1
= 6x + 24 + 1
= 6x + 25
Thus, 6(x + 4) + 1 = 6x + 25
Question 37.
5 + 8(3 + x)
Answer: 29 + 8x
Explanation:
Given the expression
5 + 8(3 + x)
= 5 + (8 × 3) + (8 × x)
= 5 + 24 + 8x
= 29 + 8x
Thus 5 + 8(3 + x) = 29 + 8x
Question 38.
x + 3 + 5x
Answer: 6x + 3
Explanation:
Given the expression
x + 3 + 5x
Combine the like terms
x + 5x + 3
6x + 3
So, x + 3 + 5x = 6x + 3
Question 39.
7y + 6 – 1 + 12y
Answer: 19y + 5
Explanation:
Given the expression
7y + 6 – 1 + 12y
Combine the like terms
7y + 12y + 6 – 1
= 19y + 5
So, 7y + 6 – 1 + 12y = 19y + 5
Question 40.
4d + 9 – d – 8
Answer: 3d + 1
Explanation:
Given the expression
4d + 9 – d – 8
Combine the like terms
4d – d + 9 – 8
3d + 1
So, 4d + 9 – d – 8 = 3d + 1
Question 41.
n + 3(n – 1)
Answer: 4n – 3
Explanation:
Given the expression
n + 3(n – 1)
n + (3 × n) – (3 × 1)
n + 3n – 3
4n – 3
So, n + 3(n – 1) = 4n – 3
Question 42.
2v + 8v – 5v
Answer: 5v
Explanation:
Given the expression
2v + 8v – 5v
Combine the like terms
v(2 + 8 – 5)
v(5) = 5v
Thus 2v + 8v – 5v = 5v
Question 43.
5(z + 4) + 5(2 – z)
Answer: 30
Explanation:
Given the expression
5(z + 4) + 5(2 – z)
= (5 × z) + (5 × 4) + (5 × 2) – (5 × z)
= 5z + 20 + 10 – 5z
Now combine the like terms
5z + 20 + 10 – 5z = 30
Question 44.
2.7(w – 5.2)
Answer: 2.7w – 14.04
Explanation:
Given the expression
2.7(w – 5.2)
= (2.7 × w) – (2.7 × 5.2)
= 2.7w – 14.04
Thus 2.7(w – 5.2) = 2.7w – 14.04
Question 45.
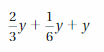
Answer:1 \(\frac{1}{2}\)y
Explanation:
Given the expression
\(\frac{2}{3}\)y + \(\frac{1}{6}\)y + y
y(\(\frac{2}{3}\) + \(\frac{1}{6}\) + 1)
= 1 \(\frac{1}{2}\)y
So, 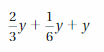 = 1 \(\frac{1}{2}\)y
= 1 \(\frac{1}{2}\)y
Question 46.
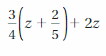
Answer: 2\(\frac{3}{4}\)z + \(\frac{3}{10}\)
Explanation:
Given the expression
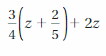
\(\frac{3}{4}\)z + \(\frac{3}{10}\) + 2z
2\(\frac{3}{4}\)z + \(\frac{3}{10}\)
Question 47.
7(x + y) – 7x
Answer: 7y
Explanation:
Given the expression
7(x + y) – 7x
= (7 × x) + (7 × y) – 7x
= 7x + 7y – 7x
= 7y
So, 7(x + y) – 7x = 7y
Question 48.
4x + 9y + 3(x + y)
Answer: 7x + 12y
Explanation:
Given the expression
4x + 9y + 3(x + y)
=4x + 9y + 3x + 3y
=4x + 3x + 9y + 3y
=7x + 12y
Thus 4x + 9y + 3(x + y) = 7x + 12y
Question 49.
YOU BE THE TEACHER
Your friend simplifies the expression. Is your friend correct? Explain your reasoning.
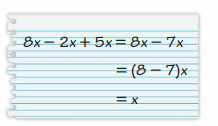
Answer: your friend is incorrect
Explanation:
8x – 2x + 5x
= 6x + 5x
= 11x
By this we can say that your friend is incorrect.
Question 50.
REASONING
Evaluate each expression by(1) using the Distributive Property and (2) evaluating inside the parentheses first. Which method do you prefer? Is your preference the same for both expressions? Explain your reasoning.

Answer:
a. 2(3.22 – 0.12)
We can solve this by using the Distributive Property
= 2(3.22) – 2(0.12)
= 6.44 – 0.24
= 6.20
2(3.22 – 0.12) = 6.20
b. 12(\(\frac{1}{2}\) + \(\frac{2}{3}\))
We can solve this by using the Distributive Property
(12 × \(\frac{1}{2}\)) + (12 × \(\frac{2}{3}\))
= 6 + 8
= 14
12(\(\frac{1}{2}\) + \(\frac{2}{3}\)) = 14
Question 51.
DIG DEEPER!
An art club sells 42 large candles and 56 small candles.
a. Write and simplify an expression that represents the profit.
b. A large candle costs $5, and a small candle costs $3. What is the club’s profit?

Answer:
For large candles, the selling price is $10 and its making cost is $x.
So, by selling a large candle the profit is $(10 – x)
Again for small candles, the selling price is $5 and its making cost is $y.
So, by selling a small candle the profit is $(5 – y)
Therefore, in a sale of 42 large candles and 56 small candles, the total profit will be, P = 42 (10 – x) + 56 (5 – y)
P = 420 – 42x + 280 – 56y
P = $(700 – 42x – 56y
Question 52.
REASONING
Find the difference between the perimeters of the rectangle and the hexagon. Interpret your answer.
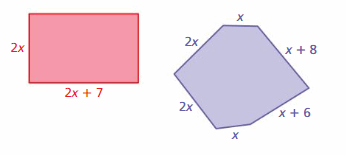
Answer:
Rectangle:
Perimeter of the Rectangle = 2l + 2w
P = 2(2x + 7) + 2(2x)
P = 4x + 14 + 4x
P = 8x + 14
Hexagon:
Perimeter of the Hexagon = 6a
P = x + x + 2x + 2x + x + 6 + x + 8
P = 8x + 14
The difference between the perimeters of the rectangle and the hexagon is (8x + 14) – (8x + 14) = 0
Question 53.
PUZZLE
Add one set of parentheses to the expression 7 . x + 3 + 8 . x + 3 . x + 8 − 9 so that it is equivalent to 2(9x + 10).
Answer:
7×(X+3)+8×X+3×X+8-9
=7×(X+3)+11×X-1
=7×X+21+11×X-1
=18×X+20
=2(9X+10)
Lesson 5.5 Factoring Expressions
EXPLORATION 1
Finding Dimensions
Work with a partner.
a. The models show the area (in square units) of each part of a rectangle. Use the models to find missing values that complete the expressions. Explain your reasoning.
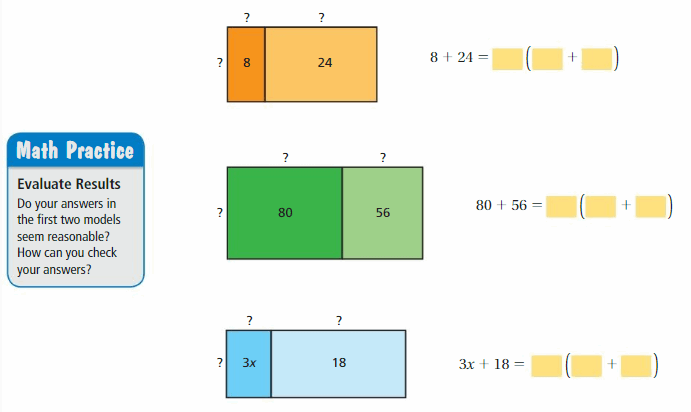
b. In part(a), check that the original expressions are equivalent to the expressions you wrote. Explain your reasoning.
c. Explain how you can use the Distributive Property to rewrite a sum of two whole numbers with a common factor.
Answer:
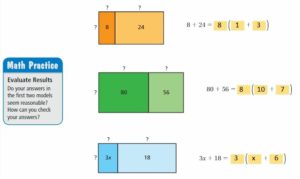
Try It
Factor the expression using the GCF.
Question 1.
9 + 15
Answer: 3
Explanation:
The factors of 9 are: 1, 3, 9
The factors of 15 are: 1, 3, 5, 15
The number does not contain any common variable factors.
Then the greatest common factor is 3.
Question 2.
60 + 45
Answer: 15
Explanation:
The factors of 45 are: 1, 3, 5, 9, 15, 45
The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
The number does not contain any common variable factors.
Then the greatest common factor is 15.
Question 3.
30 – 20
Answer: 10
Explanation:
The factors of 20 are: 1, 2, 4, 5, 10, 20
The factors of 30 are: 1, 2, 3, 5, 6, 10, 15, 30
Then the greatest common factor is 10.
Factor the expression using the GCF.
Question 4.
7x + 49
Answer: 7
Explanation:
Since 7x, 49 contain both numbers and variables, there are two steps to find the GCF.
The factors of 7 are: 1, 7
The factors of 49 are: 1, 7, 49
Then the greatest common factor is 7.
Question 5.
8y – 44
Answer: 4
Explanation:
Since 8y, 44 contain both numbers and variables, there are two steps to find the GCF.
The factors of 8 are: 1, 2, 4, 8
The factors of 44 are: 1, 2, 4, 11, 22, 44
Then the greatest common factor is 4.
Question 6.
25a + 10b
Answer: 5
Explanation:
Since 25a, 10b contain both numbers and variables, there are two steps to find the GCF.
The factors of 10 are: 1, 2, 5, 10
The factors of 25 are: 1, 5, 25
Then the greatest common factor is 5.
Self-Assessment for Concepts & Skills
Solve each exercise. Then rate your understanding of the success criteria in your journal.
FACTORING EXPRESSIONS
Factor the expression using the GCF.
Question 7.
16 + 24
Answer: 8
Explanation:
The factors of 16 are: 1, 2, 4, 8, 16
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
Then the greatest common factor is 8.
Question 8.
49 – 28
Answer: 7
Explanation:
The factors of 28 are: 1, 2, 4, 7, 14, 28
The factors of 49 are: 1, 7, 49
Then the greatest common factor is 7.
Question 9.
8y + 14
Answer: 2
Explanation:
Since 8y, 14 contain both numbers and variables, there are two steps to find the GCF.
The factors of 8 are: 1, 2, 4, 8
The factors of 14 are: 1, 2, 7, 14
Then the greatest common factor is 2.
Question 10.
WHICH ONE DOESN’T BELONG?
Which expression does not belong with the other three? Explain your reasoning.
![]()
Answer: 6(4n + 3)
Explanation:
i. 3(8n + 12)
= 24n + 36
ii. 4(6n + 9)
24n + 36
iii. 6(4n + 3)
24n + 18
iv. 12(2n + 3)
24n + 36
Thus the third expression does not belong to the other three.
Question 11.
REASONING
Use what you know about factoring to explain how you can factor the expression 18x + 30y + 9z. Then factor the expression.
Answer: 3 (6x + 10y + 3z)
Explanation:
Factoring is a mathematical representation of the expression with the help of common factors.
In this expression, we have given terms and their coefficients. Since we cannot factorize the terms, they will be intact in the process.
We can factorize this expression with the help of prime numbers:
2 × 3 × 3 × x + 2 × 3 × 5 × y + 3 × 3 × z
And finally, we will be able to obtain common factor from this expression:
3 ( 6x + 10y + 3z)
Question 12.
CRITICAL THINKING
Identify the GCF of the terms (x . x) and (4 . x). Explain your reasoning. Then use the GCF to factor the expression x2 + 4x.
Answer:
x2 + 4x
= x(x + 4)
The factors of 1 are: 1
The factors of 4 are: 1, 2, 4
Then the greatest common factor is 1.
Self-Assessment for Problem Solving
Solve each exercise. Then rate your understanding of the success criteria in your journal.
Question 13.
A youth club receives a discount on each pizza purchased for a party. The original price of each pizza is x dollars. The club leader purchases 8 pizzas for a total of (8x − 32) dollars. Factor the expression. What can you conclude about the discount?
Answer:
Given that,
A youth club receives a discount on each pizza purchased for a party.
The original price of each pizza is x dollars.
The club leader purchases 8 pizzas for a total of (8x − 32) dollars.
Question 14.
Three crates of food are packed on a shuttle departing for the Moon. Each crate weighs x pounds. On the Moon, the combined weight of the crates is (3x − 81) pounds. What can you conclude about the weight of each crate on the Moon?

Answer:
Three crates of food are packed on a shuttle departing for the Moon.
Each crate weighs x pounds. On the Moon, the combined weight of the crates is (3x − 81) pounds.
The factors of 3 are: 1, 3
The factors of 81 are: 1, 3, 9, 27, 81
Then the greatest common factor is 3.
Factoring Expressions Homework & Practice 5.5
Review & Refresh
Use the Distributive Property to simplify the expression.
Question 1.
2(n + 8)
Answer: 2n + 16
Explanation:
Given the expression 2(n + 8)
The distributive property explains that multiplying two numbers (factors) together will result in the same thing as breaking up one factor into two addends, multiplying both addends by the other factor, and adding together both products.
(2 × n) + (2 × 8)
= 2n + 16
Question 2.
3(4 + m)
Answer: 12 + 3m
Explanation:
The distributive property explains that multiplying two numbers (factors) together will result in the same thing as breaking up one factor into two addends, multiplying both addends by the other factor, and adding together both products.
3(4 + m)
= (3 × 4) + (3 × m)
= 12 + 3m
Question 3.
7(b – 3)
Answer: 7b – 21
Explanation:
The distributive property explains that multiplying two numbers (factors) together will result in the same thing as breaking up one factor into two addends, multiplying both addends by the other factor, and adding together both products.
7(b – 3)
= (7 × b) – (7 × 3)
= 7b – 21
Question 4.
10(4 – w)
Answer: 40 – 10w
Explanation:
The distributive property explains that multiplying two numbers (factors) together will result in the same thing as breaking up one factor into two addends, multiplying both addends by the other factor, and adding together both products.
10 (4 – w)
= (10 × 4) – (10 × w)
= 40 – 10w
Write the phrase as an expression.
Question 5.
5 plus a number p
Answer: 5 + p
Explanation:
The phrase plus indicates addition.
The Express would be 5 + p
Question 6.
18 less than a number r
Answer: 18 < r
Explanation:
The phrase less than indicates < symbol.
So the expression would be 18 < r
Question 7.
11 times a number d
Answer: 11d
Explanation:
The phrase times indicates × symbol.
So, the expression would be 11d
Question 8.
a number c divided by 25
Answer: c ÷ 25
Explanation:
The phrase divided by indicates ÷
So, the expression would be c ÷ 25
Decide whether the rates are equivalent.
Question 9.
84 feet in 12 seconds
217 feet in 31 seconds
Answer: The rates are equivalent
Explanation:
Given,
84 feet in 12 seconds
217 feet in 31 seconds
Here we have to check whether the rates are equivalent or not.
84 feet in 12 seconds = 7 : 1
217 feet in 31 seconds = 7 : 1
Thus the rates are equivalent.
Question 10.
12 cups of soda for every 54 cups of juice
8 cups of soda for every 36 cups of juice
Answer: the rates are equivalent
Explanation:
Given,
12 cups of soda for every 54 cups of juice
8 cups of soda for every 36 cups of juice
Here we have to check whether the rates are equivalent or not.
12 cups of soda for every 54 cups of juice = 2 : 9
8 cups of soda for every 36 cups of juice = 2 : 9
Thus the rates are equivalent.
Match the decimal with its equivalent percent.
Question 11.
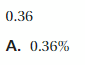
Answer: C
Explanation:
The fraction form of the decimal 0.36 is \(\frac{36}{100}\)
\(\frac{36}{100}\) × 100 = 36%
Thus the equivalent percent is option C.
Question 12.
Answer: B
Explanation:
The fraction form of the decimal 3.6 is \(\frac{36}{10}\)
\(\frac{36}{10}\) × 100 = 36 × 10 = 360%
Thus the equivalent percent is option B.
Question 13.
Answer: A
Explanation:
The fraction form of the decimal 0.0036 is \(\frac{36}{10000}\)
\(\frac{36}{10000}\) × 100 = \(\frac{36}{100}\) = 0.36%
Thus the equivalent percent is option A.
Question 14.
Answer: B
Explanation:
Explanation:
The fraction form of the decimal 0.0036 is \(\frac{36}{1000}\)
\(\frac{36}{1000}\) × 100 = \(\frac{36}{10}\) =3.6%
Thus the equivalent percent is option D.
Concepts, Skills, & Problem Solving
FINDING DIMENSIONS
The model shows the area (in square units) of each part of a rectangle. Use the model to find missing values that complete the expression. Explain your reasoning. (See Exploration 1, p. 227.)
Question 15.
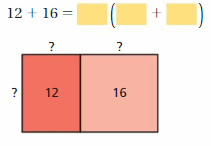
Answer:4(3 + 4)
Explanation:
We can find the area of the rectangle by using the distributive property.
Let us take 4 as the common factor
(12 + 16) = 4(3 + 4)
Question 16.
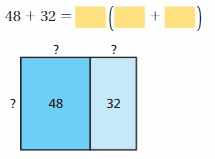
Answer: 8(6 + 4)
Explanation:
We can find the area of the rectangle by using the distributive property.
Let us take 8 as a common factor
48 + 32 = 8 (6 + 4)
FACTORING NUMERICAL EXPRESSIONS
Factor the expression using the GCF.
Question 17.
7 + 14
Answer: 7
Explanation:
The factors of 7 are: 1, 7
The factors of 14 are: 1, 2, 7, 14
Then the greatest common factor is 7.
Question 18.
12 + 42
Answer: 6
Explanation:
The factors of 12 are: 1, 2, 3, 4, 6, 12
The factors of 42 are: 1, 2, 3, 6, 7, 14, 21, 42
Then the greatest common factor is 6.
Question 19.
22 + 11
Answer: 11
Explanation:
The factors of 11 are: 1, 11
The factors of 22 are: 1, 2, 11, 22
Then the greatest common factor is 11.
Question 20.
70 + 95
Answer: 5
Explanation:
The factors of 70 are: 1, 2, 5, 7, 10, 14, 35, 70
The factors of 95 are: 1, 5, 19, 95
Then the greatest common factor is 5.
Question 21.
60 – 36
Answer: 12
Explanation:
The factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18, 36
The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Then the greatest common factor is 12.
Question 22.
100 – 80
Answer: 20
Explanation:
The factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
The factors of 100 are: 1, 2, 4, 5, 10, 20, 25, 50, 100
Then the greatest common factor is 20.
Question 23.
84 + 28
Answer: 28
Explanation:
The factors of 28 are: 1, 2, 4, 7, 14, 28
The factors of 84 are: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Then the greatest common factor is 28.
Question 24.
48 + 80
Answer: 16
Explanation:
The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
The factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20, 40, 80
Then the greatest common factor is 16.
Question 25.
19 + 95
Answer: 19
Explanation:
The factors of 19 are: 1, 19
The factors of 95 are: 1, 5, 19, 95
Then the greatest common factor is 19.
Question 26.
44 – 11
Answer: 11
Explanation:
The factors of 11 are: 1, 11
The factors of 44 are: 1, 2, 4, 11, 22, 44
Then the greatest common factor is 11.
Question 27.
18 – 12
Answer: 6
Explanation:
The factors of 12 are: 1, 2, 3, 4, 6, 12
The factors of 18 are: 1, 2, 3, 6, 9, 18
Then the greatest common factor is 6.
Question 28.
48 + 16
Answer: 16
Explanation:
The factors of 16 are: 1, 2, 4, 8, 16
The factors of 48 are: 1, 2, 3, 4, 6, 8, 12, 16, 24, 48
Then the greatest common factor is 16.
Question 29.
98 – 70
Answer: 14
Explanation:
The factors of 70 are: 1, 2, 5, 7, 10, 14, 35, 70
The factors of 98 are: 1, 2, 7, 14, 49, 98
Then the greatest common factor is 14.
Question 30.
58 + 28
Answer: 2
Explanation:
The factors of 28 are: 1, 2, 4, 7, 14, 28
The factors of 58 are: 1, 2, 29, 58
Then the greatest common factor is 2.
Question 31.
72 – 39
Answer: 3
Explanation:
The factors of 39 are: 1, 3, 13, 39
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Then the greatest common factor is 3.
Question 32.
69 + 84
Answer: 3
Explanation:
The factors of 69 are: 1, 3, 23, 69
The factors of 84 are: 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42, 84
Then the greatest common factor is 3.
Question 33.
REASONING
The whole numbers a and b are divisible by c, where b is greater than a. Is a + b divisible by c ? Is b − a divisible by c ? Explain your reasoning.
Answer:
Let the whole numbers a and b be 12 and 54
Let c be 6.
In this case b is greater than a.
Now let us check whether and b are divisible by c.
a + b ÷ c:
12 + 54 ÷ 6
66 ÷ 6 = 11
b – a ÷ c:
54 – 12 ÷ 6
42 ÷ 6 = 7
Question 34.
MULTIPLE CHOICE
Which expression is not equivalent to 81x + 54?
A. 27(3x + 2)
B. 3(37x + 18)
C. 9(9x + 6)
D. 6(13x + 9)
Answer: B. 3(37x + 18), D. 6(13x + 9)
Explanation:
Given the expression 81x + 54
A. 27(3x + 2)
= (27 × 3x) + (27 × 2)
= 81x + 54
B. 3(37x + 18)
= 111x + 54
C. 9(9x + 6)
= 81x + 54
D. 6(13x + 9)
78x + 54
Thus the expression is not equivalent to 81x + 54 are option B and D.
FACTORING ALGEBRAIC EXPRESSIONS
Factor the expression using the GCF.
Question 35.
2x + 10
Answer: 2
Explanation:
Since 2x, 10 contain both numbers and variables, there are two steps to find the GCF.
The factors of 2 are: 1, 2
The factors of 10 are: 1, 2, 5, 10
Then the greatest common factor is 2.
Question 36.
15x + 6
Answer: 3
Explanation:
Since 15x, 6 contain both numbers and variables, there are two steps to find the GCF.
The factors of 6 are: 1, 2, 3, 6
The factors of 15 are: 1, 3, 5, 15
Then the greatest common factor is 3.
Question 37.
26x – 13
Answer: 13
Explanation:
Since 26x, 13 contain both numbers and variables, there are two steps to find the GCF.
The factors of 13 are: 1, 13
The factors of 26 are: 1, 2, 13, 26
Then the greatest common factor is 13
Question 38.
50x – 60
Answer: 10
Explanation:
Since 50x, 60 contain both numbers and variables, there are two steps to find the GCF.
The factors of 50 are: 1, 2, 5, 10, 25, 50
The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Then the greatest common factor is 10.
Question 39.
36x + 9
Answer: 9
Explanation:
Since 36x, 9 contain both numbers and variables, there are two steps to find the GCF.
The factors of 9 are: 1, 3, 9
The factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18, 36
Then the greatest common factor is 9
Question 40.
14x – 98
Answer: 14
Explanation:
Since 14x, 98 contain both numbers and variables, there are two steps to find the GCF.
The factors of 14 are: 1, 2, 7, 14
The factors of 98 are: 1, 2, 7, 14, 49, 98
Then the greatest common factor is 14.
Question 41.
18p + 26
Answer: 2
Explanation:
Since 18p, 26 contain both numbers and variables, there are two steps to find the GCF.
The factors of 18 are: 1, 2, 3, 6, 9, 18
The factors of 26 are: 1, 2, 13, 26
Then the greatest common factor is 2.
Question 42.
16m + 40
Answer: 8
Explanation:
Since 16m, 40 contain both numbers and variables, there are two steps to find the GCF.
The factors of 16 are: 1, 2, 4, 8, 16
The factors of 40 are: 1, 2, 4, 5, 8, 10, 20, 40
Then the greatest common factor is 8.
Question 43.
24 + 72n
Answer: 24
Explanation:
Since 24, 72n contain both numbers and variables, there are two steps to find the GCF.
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
The factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72
Then the greatest common factor is 24.
Question 44.
50 + 65h
Answer: 5
Explanation:
Since 50, 65h contain both numbers and variables, there are two steps to find the GCF.
The factors of 50 are: 1, 2, 5, 10, 25, 50
The factors of 65 are: 1, 5, 13, 65
Then the greatest common factor is 5.
Question 45.
76d – 24
Answer: 4
Explanation:
Since 76d, 24 contain both numbers and variables, there are two steps to find the GCF.
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
The factors of 76 are: 1, 2, 4, 19, 38, 76
Then the greatest common factor is 4.
Question 46.
27 – 45c
Answer: 9
Explanation:
Since 27, 45c contains both numbers and variables, there are two steps to find the GCF.
The factors of 27 are: 1, 3, 9, 27
The factors of 45 are: 1, 3, 5, 9, 15, 45
Then the greatest common factor is 9.
Question 47.
18t + 38x
Answer: 2
Explanation:
Since 18t, 38x contains both numbers and variables, there are two steps to find the GCF.
The factors of 18 are: 1, 2, 3, 6, 9, 18
The factors of 38 are: 1, 2, 19, 38
Then the greatest common factor is 2.
Question 48.
90y + 65z
Answer: 5
Explanation:
Since 90y, 65z contains both numbers and variables, there are two steps to find the GCF.
The factors of 65 are: 1, 5, 13, 65
The factors of 90 are: 1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90
Then the greatest common factor is 5.
Question 49.
10x – 25y
Answer: 5
Explanation:
Since 10x, 25y contains both numbers and variables, there are two steps to find the GCF.
The factors of 10 are: 1, 2, 5, 10
The factors of 25 are: 1, 5, 25
Then the greatest common factor is 5.
Question 50.
24y + 88x
Answer: 8
Explanation:
Since 24y, 88x contains both numbers and variables, there are two steps to find the GCF.
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
The factors of 88 are: 1, 2, 4, 8, 11, 22, 44, 88
Then the greatest common factor is 8.
Question 51.
OPEN-ENDED
Use the Distributive Property to write two expressions that are equivalent to 8x + 16.
Answer: 8(x + 2), 4(2x + 4)
Explanation:
By using the Distributive Property we can write 8x + 16 in two ways.
8x + 16
Take 8 as a common factor
8(x + 2)
Next take 4 as a common factor
4(2x + 4)
The expressions 8(x + 2) and 4(2x + 4) are equivalent to 8x + 16
MATCHING
Match the expression with an equivalent expression.
Question 52.
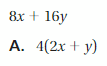
Answer: C
Explanation:
Given the expression 8x + 16y
Let us take 4 as a common factor.
4(2x + 4y)
Thus the equivalent expression is option C.
Question 53.
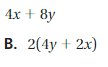
Answer: B
Explanation:
Given the expression 4x + 8y
Let us take 2 as a common factor.
4x + 8y = 2(4y + 2x)
Thus the equivalent expression is option B.
Question 54.
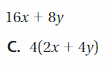
Answer: D
Explanation:
Given the expression 16x + 8y
Let us take 8 as a common factor.
16x + 8y = 8(2x + y)
This can also be written as 8(y + 2x)
Thus the equivalent expression is option D.
Question 55.
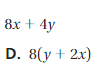
Answer: A
Explanation:
Given the expression 8x + 4y
Let us take 4 as a common factor.
8x + 4y = 4(2x + y)
Thus the equivalent expression is option A.
Question 56.
YOU BE THE TEACHER
Your friend factors the expression 24x + 56. Is your friend correct? Explain your reasoning.
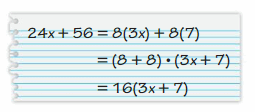
Answer: your friend is incorrect
Explanation:
Given the expression 24x + 56
Take 8 as the common factor from the expression.
24x + 56 = 8(3x + 7)
By this, we can say that your friend is incorrect.
Question 57.
MODELING REAL LIFE
You sell soup mixes for a fundraiser. For each soup mix you sell, the company that makes the soup receives x dollars, and you receive the remaining amount. You sell 16 soup mixes for a total of (16x + 96) dollars. How much money do you receive for each soup mix that you sell?
Answer: $6
Explanation:
Here, the cost price of each soup = x dollars
The cost price of 16 soup = 16 x
The selling price of 16 soup = 16 x + 96
Since, the total money received for 16 soup = The selling price of 16 soup – The cost price of 16 soup
= 16 x + 96 – 16 x
= 96
Thus, the total money received for 16 soup = 96 dollars
⇒ The total money received for 1 soup = 96/16 dollars
⇒ The total money received for 1 soup = 6 dollars
Hence, for each soup 6 dollars is received.
Question 58.
PROBLEM SOLVING
A clothing store is having a sale on holiday socks. Each pair of socks costs x dollars. You leave the store with 6 pairs of socks and spend a total of (6x − 14) dollars. You pay with $40. How much change do you receive? Explain your reasoning.

Answer: $14
Explanation:
Given,
A clothing store is having a sale on holiday socks. Each pair of socks costs x dollars.
You leave the store with 6 pairs of socks and spend a total of (6x − 14) dollars.
You pay with $40.
Since, the cost of 1 pair of socks = x
The cost of 6 pair of socks = 6 x
Total amount spend = $ 40
According to the question,
6 x – 14 = 40
6 x = 40 + 14
6 x = 54
x = 9
Thus, the original price of one pair of socks = $ 9
The original price of 6 pairs of socks = $ 54
Hence, the total change = original price of socks – the price of socks in the sale = 54 – 40 = $ 14
Question 59.
STRUCTURE
You buy 37 concert tickets for $8 each, and then sell all 37 tickets for $11 each. The work below shows two ways you can determine your profit. Describe each solution method. Which do you prefer? Explain your reasoning.

Answer:
Given,
You buy 37 concert tickets for $8 each, and then sell all 37 tickets for $11 each.
I prefer the second method which is simplified using the distributive property.
Number of concert tickets = 37
Actual price = $8
selling price = $11
Profit = Number of tickets (selling price – cost price)
P = 37 (11 – 8)
P = 37(3)
P = $111
Question 60.
NUMBER SENSE
The prime factorizations of two numbers are shown, where a and b represent prime numbers. Write the sum of the two numbers as an expression of the form ![]() . Explain your reasoning.
. Explain your reasoning.
![]()
Answer:
Let us consider a and b are 2 and 5
Number 1:
2 × 11 × 5 × a
Number 2:
7 × b × 3 × 3
14 (2 + 5) = 140
Algebraic Expressions and Properties Connecting Concepts
Connecting Concepts
Using the Problem-Solving Plan
Question 1.
A store sells 18 pairs of the wireless earbuds shown. Customers saved a total of $882 on the earbuds. Find the original price of the earbuds.
Understand the problem.
You know the percent discount on a pair of wireless earbuds, the number of pairs of earbuds sold, and the total amount of money that customers saved. You are asked to find the original price of the earbuds.

Make a plan
First, write an expression that represents the total amount of money that customers pay for the earbuds. Then factor the expression to find the discount (in dollars) on each pair of earbuds. Finally, solve a percent problem to find the original price.
Solve and check.
Use the plan to solve the problem. Then check your solution.
Answer:
Number of pairs = 18
Amount saved = $882
Let d be the cost of the wireless earbuds
So, the expression would be 18d + 882
Question 2.
All of the weight plates in a gym are labeled in kilograms. You want to convert the weights to pounds. Write an expression to find the number of pounds in z kilograms. Then find the weight in pounds of a plate that weighs 20.4 kilograms.

Answer:
All of the weight plates in a gym are labeled in kilograms. You want to convert the weights to pounds
Convert from kilograms to pounds
1 kg = 2.20 pounds
The expression would be 2.20z
Now we have to find the weight of 20.4 kilograms to pounds.
20.4kg = 2.20 × 20.4
= 44.97 pounds
Question 3.
You buy apple chips and banana chips in the ratio of 2 : 7.
a. How many ounces of banana chips do you buy when you buy n ounces of apple chips? Explain.
Answer:
The ratio of apple chips and banana chips = 2 : 7
Apple chips = 2
Banana chips = 7
2 + 7 = 9
n/2 = 9
n = 18
18 ounces of apple chips
n/7 = 9
n = 9 × 7
n = 63
63 ounces of banana chips for 18 ounces of apple chips.
b. You buy 12 ounces of apple chips. How many ounces of banana chips do you buy?
Answer:
You buy 12 ounces of apple chips.
The ratio of apple chips and banana chips = 2 : 7
Apple chips = 2x
Banana chips = 7x
2 + 7 = 9
n = 12
For 12 ounces of apple chips you buy 42 ounces of banana chips
Performance Task
Describing Change
At the beginning of this chapter, you watched a STEAM video called “Shadow Drawings.” You are now ready to complete the performance task related to this video, available at BigIdeasMath.com. Be sure to use the problem-solving plan as you work through the performance task.

Algebraic Expressions and Properties Chapter Review
Review Vocabulary
Write the definition and give an example of each vocabulary term.
Graphic Organizers
You can use an Example and Non-Example Chartto list examples and non-examples of a concept. Here is an Example and Non-Example Chart for the CommutativeProperty of Addition.

Choose and complete a graphic organizer to help you study the concept.
- algebraic expressions
- variable
- Commutative Property of Multiplication
- Associative Property of Addition
- Associative Property of Multiplication
- Addition Property of Zero
- Multiplication Property of Zero
- Multiplication Property of One
- Distributive Property

Chapter Self-Assessment
As you complete the exercises, use the scale below to rate your understanding of the success criteria in your journal.

5.1 Algebraic Expressions (pp. 201 – 208)
Identify the terms, coefficients, and constants in the expression.
Question 1.
9x + 2 + 8y
Answer:
2 – constant
9, 8 – coefficient
x, y – variable or term
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 2.
3x2 + x + 7
Answer:
7 – constant
3, 1 – coefficient
x – variable or term
2 is the exponent
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
An exponent refers to the number of times a number is multiplied by itself.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 3.
![]()
Answer:
1 – constant
7, 1/4 – coefficient
q – variable or term
A term without a variable is called a constant.
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Evaluate the expression when x = 20, y = 4, and z = 7.
Question 4.
x ÷ 5
Answer: 4
Explanation:
Given expression is x ÷ 5
Where x = 20
20 ÷ 5 = 4
Thus x ÷ 5 = 4
Question 5.
12 – z
Answer: 5
Explanation:
Given expression is 12 – z
Where z = 7
12 – z
= 12 – 7
= 5
Thus 12 – z = 5
Question 6.
4y
Answer: 16
Explanation:
The given expression is 4y
Where
y = 4
4y = 4(4) = 16
Question 7.
y + x
Answer: 24
Explanation:
Given expression is y + x
Where
y = 4
x = 20
y + x
= 4 + 20 = 24
Thus y + x = 24
Question 8.
x . z
Answer: 80
Explanation:
Given expression is x . z
Where
x = 20
z = 7
x . z = 20 × 7 = 140
Thus x . z = 140
Question 9.
x – y
Answer: 16
Explanation:
Given expression is x – y
Where
y = 4
x = 20
20 – 4 = 16
Thus x – y = 16
Question 10.
3z + 8
Answer: 29
Explanation:
Given expression is 3z + 8
Where
z = 7
3z + 8 = 3(7) + 8
= 21 + 8
= 29
Thus 3z + 8 = 29
Question 11.
8y – x
Answer: 12
Explanation:
Given expression is 8y – x
Where
y = 4
x = 20
8y – x = 8(4) – 20
= 32 – 20
= 12
Thus 8y – x = 12
Question 12.
![]()
Answer:
Explanation:
Given expression is ![]()
Where
y = 4
x = 20
(20)²/4
= (20 × 20)/4
= 5 × 20
= 100
Question 13.
The amount earned (in dollars) for recycling pounds of copper is 2p. How much do you earn for recycling 28 pounds of copper?
Answer: 56
Explanation:
Given,
The amount earned (in dollars) for recycling pounds of copper is 2p.
Substitute the value of p in the expression.
p = 28
2p = 2(28) = 56
Question 14.
While playing a video game, you score p game points and b triple bonus points. An expression for your score is p + 3b. What is your score when you earn 245 game points and 20 triple bonus points?

Answer:
Given,
While playing a video game, you score p game points and b triple bonus points. An expression for your score is p + 3b.
p = 245
b = 20
Substitute the value of p and b in the given expression
p + 3b = 245 + 3(22)
245 + 66 = 311
Question 15.
Tickets for a baseball game cost a dollars for adults and c dollars for children. The expression 2a + 3c represents the cost (in dollars) for a family to go to the game. What is the cost for the family when an adult ticket is $17 and a child ticket is $12?
Answer:
Given,
Tickets for a baseball game cost a dollars for adults and c dollars for children.
The expression 2a + 3c represents the cost (in dollars) for a family to go to the game.
a = 17
c = 12
2a + 3c
Substitute the value of a and c in the given expression
= 2(17) + 3(12)
= 34 + 36
= 70
Question 16.
Add one set of parentheses to the expression 2x2 + 4 − 5 so that the value of the expression is 75 when x = 6.
Answer:
2x2 + 4 − 5
x = 6
2(6)2 + 4 − 5
= 2(36) – 1
= 72 – 1
= 71
Add 4 to the expression to get the value 75
2x2 + 4 − 5 + 4
x = 6
2(6)2 + 4 − 5 + 4
= 2(36) – 1 + 4
= 72 – 1 + 4
= 71 + 4
= 75
5.2 Writing Expressions (pp. 209–214)
Write the phrase as an expression.
Question 17.
9 fewer than 23
Answer: 9 – 23
Explanation:
The phrase “fewer than” represents – symbol
Thus the expression would be 9 – 23
Question 18.
6 more than the quotient of 15 and 3
Answer: 6 + (15 ÷ 3)
Explanation:
The phrase more than represents ‘+’ and quotient represents ‘÷’
Thus the expression would be 6 + (15 ÷ 3)
Question 19.
the product of a number d and 32
Answer: 32d
Explanation:
The phrase product represents ‘×’ symbol.
Thus the expression would be 32d
Question 20.
a number t decreased by 17
Answer: d – 17
Explanation:
The phrase “decreased” represents ‘-‘ symbol.
Thus the expression would be d – 17
Question 21.
Your basketball team scored 4 fewer than twice as many points as the other team.
a. Write an expression that represents the number of points your team scored.
Answer:
Your basketball team scored 4 fewer than twice as many points, x, as the other team.
n = 2x – 4
b. The other team scored 24 points. How many points did your team score?
Answer: 14
Explanation:
The other team scored 24 points i.e. n=24.
24 = 2x – 4
2x = 24 + 4
2x = 28
x = 28/2
x = 14
Thus the team score 14 points.
Question 22.
The boiling temperature (in degrees Celsius) of platinum is 199 more than four times the boiling temperature (in degrees Celsius) of zinc.
a. Write an expression that represents the boiling temperature (in degrees Celsius) of platinum.
Answer: P = 199 + 4z
b. The boiling temperature of zinc is 907 degrees Celsius. What is the boiling temperature of platinum?
Answer:
The boiling temperature of zinc is 907 degrees Celsius.
P = 199 + 4z
P = 199 + 4(907)
P = 3827
Question 23.
Write an algebraic expression with two variables, x and y, that has a value of 50 when x = 3 and y = 5. (pp. 215–220)
Answer: 5x + 7y = 50
Explanation:
Let us assume that the algebraic expression is 5x + 7y = 50
Where x = 3 and y = 5
5(3) + 7(5) = 50
15 + 35 = 50
50 = 50
Our assumption is correct.
5.3 Properties of Addition and Multiplication
Simplify the expression. Explain each step.
Question 24.
10 + (2 + y)
Answer: 12 + y
Explanation:
Given the expression 10 + (2 + y)
Combine the like terms
10 + 2 + y = 12 + y
Question 25.
(21 + b) + 1
Answer: 22 + b
Explanation:
Given the expression (21 + b) + 1
Combine the like terms
21+ 1 + b
22 + b
Question 26.
3(7x)
Answer: 21x
Explanation:
Given the expression 3(7x)
3 × 7x = 21x
Question 27.
1(3.2w)
Answer: 3.2w
Explanation:
Given the expression 1(3.2w)
1 × 3.2w = 3.2w
Question 28.
5.3 + (w + 1.2)
Answer: 6.5 + w
Explanation:
Given the expression 5.3 + (w + 1.2)
Combine the like terms
5.3 + 1.2 + w
= 6.5 + w
Question 29.
(0 + t) + 9
Answer: t + 9
Explanation:
Given the expression (0 + t) + 9
Combine the like terms
(0 + t) + 9 = t + 9
Question 30.
The expression 7 + 3x+ 4 represents the perimeter of the triangle. Simplify the expression.
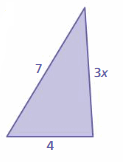
Answer:
Given,
The expression 7 + 3x+ 4 represents the perimeter of the triangle.
Combine the like terms
7 + 3x+ 4 = 11 + 3x
Question 31.
Write an algebraic expression that can be simplified using the Associative Property of Addition.
Answer:
Associative property of addition: Changing the grouping of addends does not change the sum. For example, ( 2 + 3 ) + 4 = 2 + ( 3 + 4 ) (2 + 3) + 4 = 2 + (3 + 4) (2+3)+4=2+(3+4) left parenthesis, 2, plus, 3, right parenthesis, plus, 4, equals, 2, plus, left parenthesis, 3, plus, 4, right parenthesis.
5.4 The Distributive Property
Use the Distributive Property to simplify the expression.
Question 32.
2(x + 12)
Answer:
We can simplify the expression by using the Distributive Property.
The distributive property explains that multiplying two numbers together will result in the same thing as breaking up one factor into two addends, multiplying both addends by the other factor, and adding together both products.
2(x + 12) = 2 × x + 2 × 12
= 2x + 24
Question 33.
11(4b – 3)
Answer:
Given the expression 11(4b – 3)
We can simplify the expression by using the Distributive Property.
The distributive property explains that multiplying two numbers together will result in the same thing as breaking up one factor into two addends, multiplying both addends by the other factor, and adding together both products.
11(4b – 3) = 11 × 4b – 11 × 3
= 44b – 33
Question 34.
8(s – 1)
Answer:
Given the expression 8(s – 1)
We can simplify the expression by using the Distributive Property.
The distributive property explains that multiplying two numbers together will result in the same thing as breaking up one factor into two addends, multiplying both addends by the other factor, and adding together both products.
8(s – 1) = 8 × s – 8 × 1
= 8s – 8
Question 35.
6(6 + y)
Answer:
Given the expression 6(6 + y)
We can simplify the expression by using the Distributive Property.
The distributive property explains that multiplying two numbers together will result in the same thing as breaking up one factor into two addends, multiplying both addends by the other factor, and adding together both products.
6(6 + y) = 6 × 6 + 6 × y
36 + 6y
Simplify the expression.
Question 36.
5(n + 3) + 4n
Answer:
Given the expression 5(n + 3) + 4n
Combine the like terms
5(n + 3) + 4n
= 5 × n + 5 × 3 + 4n
= 5n + 15 + 4n
= 9n + 15
Question 37.
t + 2 + 6t
Answer:
Given the expression t + 2 + 6t
Combine the like terms
t + 2 + 6t
7t + 2
Question 38.
3z + 14 + 5z – 9
Answer:
Given the expression 3z + 14 + 5z – 9
Combine the like terms
3z + 14 + 5z – 9
8z – 5
Question 39.
A family of three goes to a salon. Each person gets a haircut and highlights. The cost of each haircut is $15, and the cost per person for highlights is x dollars. Write and simplify an expression that represents the total cost (in dollars) for the family at the salon.
Answer: 45 + 3(x)
Explanation:
Given,
A family of three goes to a salon. Each person gets a haircut and highlights.
The cost of each haircut is $15, and the cost per person for highlights is x dollars.
The expression would be 45 + 3x
Each person gets a haircut = 3 × 15 = 45
Question 40.
Each day, you take vocal lessons for v minutes and trumpet lessons for 30 minutes. Write and simplify an expression to find how many minutes of lessons you take in 4 days.

Answer:
Given,
Minutes of vocal lessons I take each day =
Minutes of trumpet lessons I take each day = 30
To write and simplify how many minutes of lessons I take in 4 days.
Solution:
Total number of minutes of lesson I take each day can be calculated by adding the minutes of lessons taken each day and can be given as:
= v + 30
The expression would be (v + 30)
So in 4 days I will take = 4(v + 30)
= 4v + 120
Thus, total minutes of lessons I take in 4 days = 4v + 120
5.5 Factoring Expressions (pp. 227 – 232)
Factor the expression using the GCF.
Question 41.
42 – 12
Answer: 6
Explanation:
The factors of 12 are: 1, 2, 3, 4, 6, 12
The factors of 42 are: 1, 2, 3, 6, 7, 14, 21, 42
Then the greatest common factor is 6.
Question 42.
15 + 35
Answer: 5
Explanation:
The factors of 15 are: 1, 3, 5, 15
The factors of 35 are: 1, 5, 7, 35
Then the greatest common factor is 5.
Question 43.
36x – 28
Answer: 4
Explanation:
The factors of 28 are: 1, 2, 4, 7, 14, 28
The factors of 36 are: 1, 2, 3, 4, 6, 9, 12, 18, 36
Then the greatest common factor is 4.
Question 44.
24 + 64x
Answer: 8
Explanation:
The factors of 24 are: 1, 2, 3, 4, 6, 8, 12, 24
The factors of 64 are: 1, 2, 4, 8, 16, 32, 64
Then the greatest common factor is 8.
Question 45.
60 – 150x
Answer: 30
Explanation:
The factors of 60 are: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
The factors of 150 are: 1, 2, 3, 5, 6, 10, 15, 25, 30, 50, 75, 150
Then the greatest common factor is 30.
Question 46.
16x + 56y
Answer: 8
Explanation:
The factors of 16 are: 1, 2, 4, 8, 16
The factors of 56 are: 1, 2, 4, 7, 8, 14, 28, 56
Then the greatest common factor is 8.
Question 47.
A soccer team receives a discount on each jersey purchased. The original price of each jersey is x dollars. The team buys 18 jerseys for a total of (18x − 36) dollars. What can you conclude about the discount?
Answer:
Given,
A soccer team receives a discount on each jersey purchased.
The original price of each jersey is x dollars.
The team buys 18 jerseys for a total of (18x − 36) dollars.
Multiply 18 with the original price after that you decrease 36 dollars.
By this, we can conclude that $36 is the discount
Question 48.
You sell apple cider for a fundraiser. For each gallon of cider you sell, the company that makes the cider receives x dollars, and you receive the remaining amount. You sell 15 gallons of cider for (15x + 45) dollars. How much money do you receive for each gallon of cider that you sell?

Answer:
Given,
You sell apple cider for a fundraiser. For each gallon of cider you sell, the company that makes the cider receives x dollars, and you receive the remaining amount.
You sell 15 gallons of cider for (15x + 45) dollars
Let x = 1
15(1) + 45 = 60
x = 2
15(2) + 45 = 30 + 45 = 75
Algebraic Expressions and Properties Practice Test
Question 1.
Identify the terms, coefficients, and constants of \(\frac{q}{3}\) + 6 + 9q.
Answer:
6 – constant
9, \(\frac{1}{3}\) – coefficient
q – variable or term
A term without a variable is called a constant.
The exponent tells us how many times the base is used as a factor
The numerical factor of a term that contains a variable is called a coefficient.
A variable is a symbol that represents one or more numbers. Each number or variable by itself, or product of numbers and variables in an algebraic expression, is called a term.
Question 2.
Evaluate 4b – a when a = 12 and b = 7.
Answer: 16
Explanation:
Given the expression 4b – a
where a = 12 and b = 7
4(7) – 12
28 – 12 = 16
Thus 4b – a = 16
Write the phrase as an expression.
Question 3.
25 more than 50
Answer: The phrase for the expression 25 more than 50 is 25 + 50
Question 4.
6 less than the quotient of 32 and a number y.
Answer: The phrase for the expression 6 less than the quotient of 32 and a number y is 6 – 32 ÷ y
Simplify the expression. Explain each step.
Question 5.
3.1 + (8.6 + m)
Answer:
Given the expression 3.1 + (8.6 + m)
Combine the like terms
3.1 + (8.6 + m)
3.1 + 8.6 + 3
11.7 + m
Question 6.
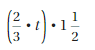
Answer:
Given the expression (\(\frac{2}{3}\) × t) × 1 \(\frac{1}{2}\)
First, convert the mixed fraction to the improper fraction
1 \(\frac{1}{2}\) = \(\frac{3}{2}\)
\(\frac{3}{2}\) × \(\frac{2}{3}\) × t
= t
Thus (\(\frac{2}{3}\) × t) × 1 \(\frac{1}{2}\) = t
Question 7.
4(x + 8)
Answer:
Given the expression 4(x + 8)
= 4 × x + 4 × 8
= 4x + 32
Question 8.
4t + 7 + 2t – 2
Answer: 6t + 5
Explanation:
Combine the like terms
4t + 7 + 2t – 2
6t + 5
Thus 4t + 7 + 2t – 2 = 6t + 5
Factor the expression using the GCF.
Question 9.
18 + 24
Answer:
Find the GCF for 18, 24
The factors of 18 are 1, 2, 3, 6, 9, 18
The factors of 24 are 1, 2, 3, 4, 6, 8, 12, 24
The common factors are 1, 2, 3, 6.
Thus the GCF of 18 + 24 is 6.
Question 10.
15x + 20
Answer:
Since 15x, 20 contain both numbers and variables, there are two steps to find the GCF.
Find the GCF fo the numerical part 15, 20
The factors of 20 are 1, 2, 4, 5, 10, 20
The factors of 15 are 1, 3, 5, 15
The number do not contain any common variable factors.
The greatest common factor is 5
Question 11.
32x – 40y
Answer: 8
Explanation:
Since 32x, 40y contain both numbers and variables, there are two steps to find the GCF.
Find the GCF for the numerical part 32, 40
The factors of 32 are 1, 2, 4, 8, 16, 32
The factors of 40 are: 1, 2, 4, 5, 8, 10, 20, 40
The number do not contain any common variable factors.
Then the greatest common factor is 8.
Question 12.
Playing time is added at the end of a soccer game to make up for stoppages. An expression for the length (in minutes) of a 90-minute soccer game with minutes of stoppage time is 90 + x. How long is a game with 4 minutes of stoppage time?

Answer: 94
Explanation:
Given,
Playing time is added at the end of a soccer game to make up for stoppages.
An expression for the length (in minutes) of a 90-minute soccer game with minutes of stoppage time is 90 + x.
x = 4
Substitute the value of x in the expression
90 + 4 = 94
Question 13.
The expression 15 . x . 6 represents the volume of a rectangular prism with a length of 15, a width of x, and a height of 6. Simplify the expression.
Answer:
Given,
The expression 15 . x . 6 represents the volume of a rectangular prism with a length of 15, a width of x, and a height of 6.
The formula for the volume of a rectangular prism is lwh
V = 15 × x × 6
V = 90x
Question 14.
The Coiling Dragon Cliff Skywalk in China is 128 feet longer than the length x (in feet) of the Tianmen Skywalk in China. The world’s longest glass-bottom bridge, located in China’s Zhangjiajie National Park, is about 4.3 times longer than the Coiling Dragon Cliff Skywalk. Write and simplify an expression that represents the length (in feet) of the world’s longest glass-bottom bridge.

Answer:
The Coiling Dragon Cliff Skywalk in China is 128 feet longer than the length x (in feet) of the Tianmen Skywalk in China.
128 + x
The world’s longest glass-bottom bridge, located in China’s Zhangjiajie National Park, is about 4.3 times longer than the Coiling Dragon Cliff Skywalk.
(128 + x) × 4.3
128 × 4.3 + 4.3 × x
550.4 + 4.3x
Thus the expression is 4.3x + 550.4ft
Question 15.
A youth group is making and selling sandwiches to raise money. The cost to make each sandwich is dollars. The group sells 150 sandwiches for a total of (150h + 450) dollars. How much profit does the group earn for each sandwich sold?
Answer:
We are given that
Cost to make each sandwich= h dollar
The total selling price of 150 sandwiches=(150h+450 )dollars
We have to find the profit earn by the group on each sandwich sold.
Total cost for making 150 sandwiches= 150 × h
Total cost for making 150 sandwiches=150 h
Now,
Profit made by the group on 150 sandwiches
=150h+450-150h
=450 dollars
Profit earn by group for each sandwich sold= 450/150
Profit earn by group for each sandwich sold=$ 3
Question 16.
You make party favors for an event. You tie 9 inches of ribbon around each party favor. Write an expression for the number of inches of ribbon needed for n party favors. The ribbon costs $3 for each yard. Write an expression for the total cost (in dollars) of the ribbon.
Answer:
Need 9n inches of ribbon Cost is $0.75n
Since you need 9 inches per party favor and you have n party favors, the amount of ribbon you need is 9 times n inches.
So R = 9n inches
Since the ribbon costs $3 per yard and our current equation is inches, we need to do a bit of conversion.
There are 36 inches per yard and 9 inches per ribbon, so each yard of ribbon can make 36/9 = 4 ribbons for the party favors.
So the cost per party favor will be one-fourth of the cost per yard of ribbon per party favor.
So $3.00 / 4 = $0.75, making the cost equation: C = $0.75n
Algebraic Expressions and Properties Cumulative Practice
Question 1.
The student council is organizing a school fair. Council members are making signs to show the prices for admission and for each game a person can play.


Let x represent the number of games. Which expression can you use to determine the total amount (in dollars) a person pays for admission and playing x games?
A. 2.25
B. 2.25x
C. 2 + 0.25x
D. 2x + 0.25
Answer: 2 + 0.25x
Explanation:
Given the data,
The student council is organizing a school fair. Council members are making signs to show the prices for admission and for each game a person can play.
Admission fee is $2
Price per game is $0.25
Let x represent the number of games.
The expression would be the sum of admission and product of price and number of games
That is 2 + 0.25x
Thus the correct answer is option C.
Question 2.
Which ratio relationship is represented in the graph?
F. 2 cups of flour for every cup of sugar \(\frac{1}{2}\) up of sugar
G. 6 cups of flour for every 3 cups of sugar
H. 1 cup of flour for every 4 cups of sugar
I. \(\frac{1}{2}\) cup of flour for every 1 cup of sugar
Answer: 2 cups of flour for every cup of sugar \(\frac{1}{2}\) up of sugar
Explanation:
The graph represents that 2 cups of flour for every cup of sugar.
Thus the correct answer is option F.
Question 3.
At a used bookstore, you can purchase two types of books.

You can use the expression 3h + 2p to find the total cost (in dollars) for h hardcover books and p paperback books. What is the total cost (in dollars) for 6 hardcover books and 4 paperback books?

Answer:
Given expression 3h + 2p
h represents hardcover books
p represents paperback books
The cost of hardcover books is $3
The cost of paperback books is $2
3h + 2p = 3(3) + 2(2)
= 9 + 4
= 13
We have to find the total cost (in dollars) for 6 hardcover books and 4 paperback books.
The equation will be 6h + 4p
= 6(3) + 4(5)
= 18 + 20
= 38
The total cost (in dollars) for 6 hardcover books and 4 paperback books is $38.
Question 4.
Your friend divided two decimal numbers. Her work is shown in the box below. What should your friend change in order to divide the two decimal numbers correctly?

Answer: C
Explanation:
0.07 ÷ 14.56 can be written as
7 ÷ 0.1456
Thus the correct answer is option C.
Question 5.
What is the value of 4.391 + 5.954?
F. 9.12145
G. 9.245
H. 9.345
I. 10.345
Answer: 10.345
Explanation:
Add two decimal numbers 4.391 and 5.954
4.391
+5.954
10.345
Thus the correct answer is option I.
Question 6.
The circle graph shows the eye color of students in a sixth-grade class. Nine students in the class have brown eyes. How many students are in the class?
A. 4 students
B. 18 students
C. 20 students
D. 405 students
Answer: 20 students
Explanation:
By seeing the above figure we can find the number of students in the class.
The circle graph shows the eye color of students in a sixth-grade class. Nine students in the class have brown eyes.
45/9 = 5
Each student is equal to 5%
35/5 = 7 students
20/5 = 4 students
9 + 7 + 4 = 20 students
Thus the correct answer is option C.
Question 7.
Properties of Addition and Multiplication are used to simplify an expression.
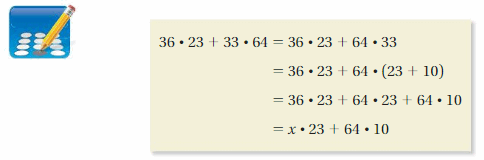
What number belongs in place of the x?
Answer:
36 × 23 + 33 × 64 = 36 × 23 + 64 × 33
= 36 × 23 + 64 × (23 + 10)
= 36 × 23 + 64 × 23 + 64 × 10
= 23(36 + 64) + 64 × 10
= 100 × 23 + 64 × 10
x = 100
Thus the number that belong to x is 100.
Question 8.
What is the prime factorization of 1350?
F. 10 . 135
G. 2 . 3 . 5
H. 6 . 225
I. 2 . 33 . 52
Answer:
The prime factorisation of 1350 is
1350 = 2 × 3 × 3 × 3 × 5 × 5
1350 = 2 . 33 . 52
Thus the correct answer is option I.
Question 9.
A horse gallops at a speed of 44 feet per second. What is the speed of the horse in miles per hour?
A. \(\frac{1}{2}\) mile per hour
B. 30 miles per hour
C. 64\(\frac{8}{15}\) miles per hour
D. 158,400 miles per hour
Answer: 30 miles per hour
Explanation:
Given,
A horse gallops at a speed of 44 feet per second.
Convert from feet per second to miles per hour.
1 foot per second = 0.68 miles per hour
44 feet per second = 30 miles per hour
Thus the correct answer is option B.
Question 10.
Which equation correctly demonstrates the Distributive Property?
F. a(b + c) = ab + ac
G. a(b + c) = ab + ac
H. a + (b + c) = (a + b) + (a + c)
I. a + (b + c) = (a + b) . (a + c)
Answer: F
Explanation:
The distributive property explains that multiplying two numbers (factors) together will result in the same thing as breaking up one factor into two addends, multiplying both addends by the other factor, and adding together both products.
a(b + c) = ab + ac
Thus the correct answer is option F.
Question 11.
Which number is equivalent to 2\(\frac{4}{5}\) . 1\(\frac{2}{7}\) ?

Answer: C
Explanation:
Convert the mixed fraction to the improper fraction.
2\(\frac{4}{5}\) = \(\frac{14}{5}\)
1\(\frac{2}{7}\) = \(\frac{9}{7}\)
Now multiply both the fractions
\(\frac{14}{5}\) × \(\frac{9}{7}\) = \(\frac{126}{35}\)
Now convert from improper fraction to the mixed fractions.
\(\frac{126}{35}\) = 3 \(\frac{3}{5}\)
Thus the correct answer is option C.
Question 12.
Which pair of numbers does not have a least common multiple of 24?
F. 2, 12
G. 3, 8
H. 6, 8
I. 12, 24
Answer: 6, 8
The least common multiple of 24 is 24.
2, 12 is 24
3, 8 is 24
6, 8 is 48
Thus the correct answer is option H.
Question 13.
Use the Properties of Multiplication to simplify the expression in an efficient way. Show your work and explain how you used the Properties of Multiplication.

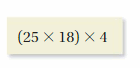
Answer:
We can use the associative property of multiplication to simplify the expression.
The associative property is a math rule that says that the way in which factors are grouped in a multiplication problem does not change the product.
(25 × 18) × 4 = 25 × (18 × 4)
450 × 4 = 1800
Question 14.
Which number is not a perfect square?
A. 64
B. 81
C. 96
D. 100
Answer: 96
Explanation:
A. 64 = 8 × 8
It is a perfect square.
B. 81 = 9 × 9
It is a perfect square.
C. 96 = 12 × 8
96 is not a perfect square.
D. 100 = 10 × 10
It is a perfect square.
Thus the correct answer is option C.
Conclusion:
I wish the article regarding the Big Ideas Math Answers Grade 6 Chapter 5 Algebraic Expressions and Properties is helpful for you. For any queries, you can ask your questions in the below-mentioned comment box. Also, share the pdf link with your friends and help them to overcome the issues in maths.