By accessing our 180 Days of Math for Fifth Grade Answers Key Day 176 regularly, students can get better problem-solving skills.
180 Days of Math for Fifth Grade Answers Key Day 176
Directions: Solve each problem.
Question 1.
85 – 37 = ___________
Answer:
Subtraction is one of the four basic arithmetic operations in mathematics. We can observe the applications of subtraction in our everyday life in different situations. For example, when we purchase fruits and vegetables for a certain amount of money say Rs. 200 and we have given an Rs. 500 note to the vendor. Now, the vendor returns the excess amount by performing subtraction such as 500 – 200 = 300. Then, the vendor will return Rs. 300.
Now we need to calculate the above-given question:
We need to subtract 37 from 85
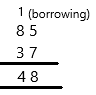
85 = Minuend; 37 = Subtrahend; 48 = Difference
Therefore, the answer is 48.
Question 2.
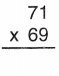
Answer:
In mathematics, multiplication is a method of finding the product of two or more numbers. It is one of the basic arithmetic operations, that we use in everyday life. The major application we can see in multiplication tables.
In arithmetic, the multiplication of two numbers represents the repeated addition of one number with respect to another. These numbers can be whole numbers, natural numbers, integers, fractions, etc. If m is multiplied by n, then it means either m is added to itself ‘n’ number of times or vice versa.
The formula for multiplication:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
– The multiplicand is the total number of objects in each group
– A multiplier is the number of equal groups
– Product is the result of multiplication of multiplier and multiplicand
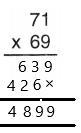
Therefore, the answer is 4899.
Question 3.
Is 9 a factor of both 63 and 89?
Answer:
we can say that the factors are the numbers (including both positive and negative numbers) that get multiplied and produce the original number. For example, when we multiply 7 and 9, we get 63, i.e. 7 × 9 = 63, where 7 and 9 are called the factors of 63. Thus, the factors of 89 are the numbers which when multiplied together produce the result as 89.
The factors of 63 are the numbers that divide the number 63 exactly without leaving any remainder. In other words, the pair factors of 63 are the numbers that are multiplied in pairs resulting in the original number 63. Since the number 63 is a composite number, 63 has more than two factors. Thus, the factors of 63 are 1, 3, 7, 9, 21 and 63.
Factors of 63 are the integers that divide the original number evenly. There are totally six factors of 63, i.e., 1, 3, 7, 9, 21, and 63.
Therefore, the positive factors of 89 are 1 and 89.
According to the above statements, 9 is the factor of 63 not for 89.
Question 4.
Arrange the numbers ¡n ascending order.
3,106; 3,601; 3,016
Answer:
In Mathematics, the process of arranging the numbers from smallest value to largest value is called ascending order. The numbers are arranged from left to right in increasing order.
The above-given numbers: 3,106; 3,601; 3,016
Now we need to arrange in ascending order.
3,016; 3,106; 3,601.
Question 5.
Simplify \(\frac{8}{12}\).
Answer:
We can write the latex sentence as in fraction form as:
8/12
We need to simplify the above fraction
– In the fraction 8/12, 8 is the numerator and 12 is the denominator.
– we assume you want to know how to simplify the numerator and denominator to their smallest values, while still keeping the same value of the fraction.
– We do this by first finding the greatest common factor of 8 and 12, which is 4.
– Then, we divide both 8 and 12 by the greatest common factor to get the following simplified fraction: 2/3
– Therefore, this equation is true:
8/12 = 2/3
– If the numerator is greater than or equal to the denominator of a fraction, then it is called an improper fraction. In that case, you could convert it into a whole number or mixed number fraction.
– 2/3 is a proper fraction.
Question 6.
3 • 5 + 5 • 7 + 2 • 9 = ___________
Answer:
In mathematics, multiplication is a method of finding the product of two or more numbers. It is one of the basic arithmetic operations, that we use in everyday life. The major application we can see in multiplication tables.
In arithmetic, the multiplication of two numbers represents the repeated addition of one number with respect to another. These numbers can be whole numbers, natural numbers, integers, fractions, etc. If m is multiplied by n, then it means either m is added to itself ‘n’ number of times or vice versa.
The formula for multiplication:
The multiplication formula is given by:
Multiplier × Multiplicand = Product
– The multiplicand is the total number of objects in each group
– A multiplier is the number of equal groups
– Product is the result of multiplication of multiplier and multiplicand
3*5=15
5*7=35
2*9=18
Now add all the above
15+35+18=68
Therefore, the answer is 68.
Question 7.
 ÷ 6 = 20
÷ 6 = 20
Answer:
Let us assume that the empty box be X
X ÷ 6 = 20
Now get the number 6 to the right-hand side then 6 will be multiplied.
X=20 * 6
X = 120
Now verify the answer we got.
120 ÷ 6 = 20
120/6=20
Therefore, the answer is verified.
Question 8.
How many minutes are there from 9: 25 A.M. to 11: 04 A.M.?
Answer:
The given timings are 9: 25 A.M. to 11: 04 A.M.
from 9: 25 A.M to 10: 25 A.M is nothing but 1 hour.
1 hour = 60 minutes
from 10: 25 A.M to 11: 04 A.M is nothing but 39 minutes.
Now add the total minutes we got:
60+39 minutes=99 minutes.
Therefore, 99 minutes are there from 9: 25 A.M. to 11: 04 A.M
Question 9.
True or false?
All squares are quadrilaterals.
Answer:
True.
Quadrilaterals are square, rectangle, parallelogram, rhombus, trapezium, kite
All squares are rectangles: True! A rectangle has opposite sides equal, and a square has all sides equal; therefore, a square has opposite sides equal! A rectangle has opposite sides equal and a square has opposite sides equal. A rectangle has four right angles and a square has four right angles. Because the attributes of a rectangle are true for a square, a square is a rectangle.
All squares are parallelograms: True, a parallelogram has opposite sides equal and so does a square (all sides are equal). A parallelogram has opposite sides and parallels so do a square.
All squares are rhombus: True because the definition of a rhombus states that all sides are equal and opposite sides are parallel. Those attributes are all true for a square as well.
Question 10.
Gary has 23 quarters in his bank. He saves 4 more quarters each week. If Gary continues to save 4 quarters each week, how many quarters will he have in 8 weeks?
|
Start |
Week 1 | Week 2 | Week 3 |
Week 4 |
| 23 | 27 | 31 | 35 | 39 |
Answer:
The number of quarters Gary has in his bank=23
The number of quarters he saves each week=4
For week 1: 23+4=27
For week 2: 27+4=31
For week 3: 31+4=35
For week 4: 35+4=39
For week 5: 39+4=43
For week 6: 43+4=47
For week 7: 47+4=51
For week 8: 51+4=55
Therefore, there are 55 quarters will have in 8 weeks.
Question 11.
The numbers 1 through 10 are written on individual cards and placed in a bag. What is the probability that you will reach into the bag and grab an odd number?
Answer:
The numbers are 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
The odd numbers are 1, 3, 5, 7, 9
Favourable outcomes=5
Total outcomes=10
Probability of an event=favourable outcomes/total outcomes
P(odd number)=5/10
P(odd number)=1/2
Therefore, the probability of grabbing an odd number from the bag is 1/2.
Question 12.
Complete the input/output table. Look for a pattern and write the rule.
| Input | 38 | 36 | 34 | 32 | 30 | 28 |
| Output | 81 | 79 | 77 |
Answer:
The arithmetic pattern is also known as the algebraic pattern. In an arithmetic pattern, the sequences are based on the addition or subtraction of the terms. If two or more terms in the sequence are given, we can use addition or subtraction to find the arithmetic pattern.
The input pattern is given:38, 36, 34, 32, 30, 28
For the input pattern, the rule is used “subtract 2 to the previous term to get the next term”.
Here, we can use the subtraction process to figure out the missing terms in the patterns.
In the pattern, the rule used is “subtract 2 to the previous term to get the next term”.
In the example given above, take the second term (79). If we subtract “2” to the second term (79), we get the third term 77.
Similarly, we can find the unknown terms in the sequence.
First missing term: The previous term is 77. Therefore, 77-2 = 75
Second missing term: The previous term is 75. So, 75-2 = 73
The third missing term: The previous term is 73. So, 73-2=71
Hence, the complete arithmetic pattern is 81, 79, 77, 75, 73, 71.
Therefore, the output result is 81, 79, 77, 75, 73, 71.