Spectrum Math Grade 8 Chapter 5 Lesson 12 Answer Key Volume: Spheres

Students can use the Spectrum Math Grade 8 Answer Key Chapter 5 Lesson 5.12 Volume: Spheres as a quick guide to resolve any of their doubts.

Spectrum Math Grade 8 Chapter 5 Lesson 5.12 Volume: Spheres Answers Key

Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³. When the diameter of a sphere is known, it can be divided by 2 and then the formula for the volume of a sphere can be used.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(7) = \(\frac{7}{2}\) = 3.5
V = \(\frac{4}{3}\)πr(3.5)³ = \(\frac{4}{3}\)π(42.875) = 179.5 cubic meters

Find the volume of each sphere. Use 3.1 4 to represent π. Round answers to the nearest hundredth.

Question 1.
a.

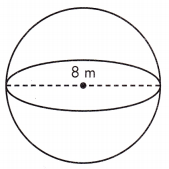
V = ____ m³
Answer: 267.95m³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, d = 8m
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(8) = 4
V = \(\frac{4}{3}\)πr(4)³ =  267.94666 m³= 267.95m³

b.

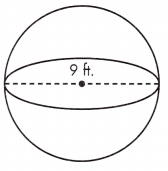
V = ____ ft.³
Answer: 373.03 ft.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, d = 9 ft.
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(9) = 4.5
V = \(\frac{4}{3}\)πr(4.5)³ =  373.032 ft.³= 373.03 ft.³

c.

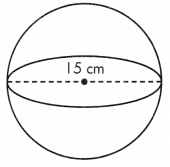
V = ____ cm³
Answer: 1766.25 cm³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, d = 15 cm
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(15) = 7.5
V = \(\frac{4}{3}\)πr(7.5)³ = 1766.25 cm³

Question 2.
a.

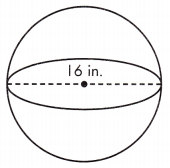
V = ____ in.³
Answer: 2143.57 in.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, d = 16 in.
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(16) = 8
V = \(\frac{4}{3}\)πr(8)³ = 2143.57333 in.³ = 2143.57 in.³

b.

V = ____ km³
Answer: 523.33 km³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
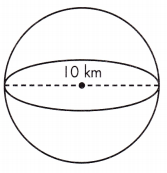
Given, d = 10 km
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(10) = 5 km
V = \(\frac{4}{3}\)πr(5)³ = 523.333 km³= 523.33 km³

c.

V = ____ m³
Answer: 4186.67 m³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
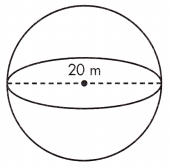
Given, d = 20 m
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(20) = 10 m
V = \(\frac{4}{3}\)πr(10)³ = 4186.66666 m³= 4168.67 m³

Question 3.
a.

V = ____ ft.³
Answer: 904.32 ft.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
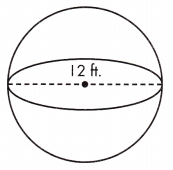
Given, d = 12 ft.
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(12) = 6 ft.
V = \(\frac{4}{3}\)πr(6)³ = 904.32 ft.³

b.

V = ____ cm³
Answer: 1436.0266 cm³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
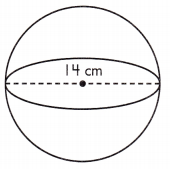
Given, d = 14 cm
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(14) = 7 cm
V = \(\frac{4}{3}\)πr(7)³ = 1436.0266 cm³= 1436.03 cm³

c.

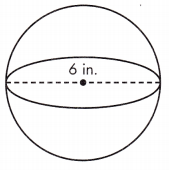
V = ____ in.³
Answer: 113.04 in.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, d = 6 in.
The radius of a sphere is half of its diameter. Find the radius, then calculate the volume.
r = \(\frac{1}{2}\)d = \(\frac{1}{2}\)(6) = 3 in.
V = \(\frac{4}{3}\)πr(3)³ = 113.04  in.³

Find the volume of each sphere. Use 3.14 to represent π. Round answers to the nearest hundredth.

Question 1.
a.

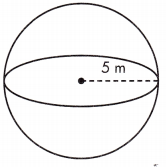
V = ____ m³
Answer: 523.33 m³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 5m
V = \(\frac{4}{3}\)πr(5)³ = 523.3333 m³= 523.33 m³

b.

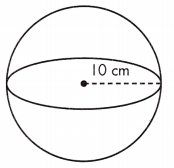
V = ____ cm³
Answer: 4186.67cm³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 10 cm
V = \(\frac{4}{3}\)πr(10)³ = 4186.6666 cm³= 4186.67 cm³

c.

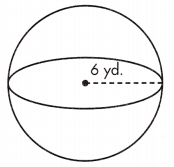
V = ____ yd.³
Answer: 904.32 yd.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 6 yd.
V = \(\frac{4}{3}\)πr(6)³ = 904.32 yd.³

Question 2.
a.

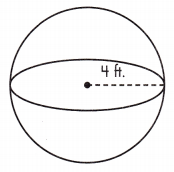
V = ____ ft.³
Answer: 267.95 ft.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 4 ft.
V = \(\frac{4}{3}\)πr(4)³ = 267.94666 ft.³= 267.95 ft.³

b.

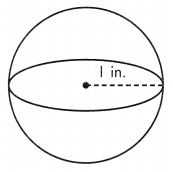
V = ____ in.³
Answer: 4.19 in.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 1 in.
V = \(\frac{4}{3}\)πr(1)³ = 4.18666 in.³= 4.19 in.³

c.

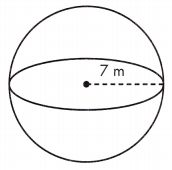
V = ____ m³
Answer: 1436.03 m³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 7 m
V = \(\frac{4}{3}\)πr(7)³ = 1436.02666 m³= 1436.03m³

Question 3.
a.

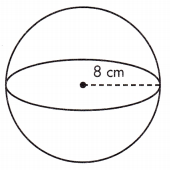
V = ____ cm³
Answer: 2143.57333 cm³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 8 cm
V = \(\frac{4}{3}\)πr(8)³ = 2143.57333 cm³= 2143.57 cm³

b.

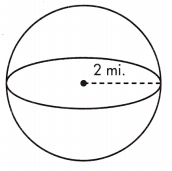
V = ____ mi.³
Answer: 33.49 mi.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 2 mi.
V = \(\frac{4}{3}\)πr(2)³ = 33.4933 mi.³= 33.49 mi.³

c.

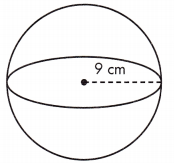
V = ____ cm³
Answer: 3052.08  cm³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 9 cm
V = \(\frac{4}{3}\)πr(9)³ = 3052.08 cm³

Question 4.
a.

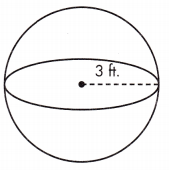
V = ____ ft.³
Answer: 113.04 ft.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 3 ft.
V = \(\frac{4}{3}\)πr(3)³ = 113.04 ft.³

b.

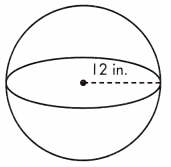
V = ____ in.³
Answer: 7234.56 in.³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 12 in.
V = \(\frac{4}{3}\)πr(12)³ = 7234.56 in.³

c.

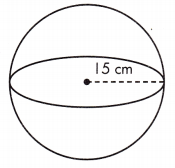
V = ____ cm³
Answer: 14130 cm³
Volume is the amount of space a three-dimensional figure occupies. The volume of a sphere is calculated as V = \(\frac{4}{3}\)πr³.
\(\frac{4}{3}\)πr³ Volume is given in cubic units or units³.
Given, r = 15 cm
V = \(\frac{4}{3}\)πr(15)³ = 14130 cm³