Spectrum Math Grade 8 Chapter 4 Lesson 3 Answer Key Functions and Linear Relationships

Students can use the Spectrum Math Grade 8 Answer Key Chapter 4 Lesson 4.3 Functions and Linear Relationships as a quick guide to resolve any of their doubts.

Spectrum Math Grade 8 Chapter 4 Lesson 4.3 Functions and Linear Relationships Answers Key

Data in tables can be used to create equations. If the table of values represents a function, a linear relationship in the form of y = mx + b exists.

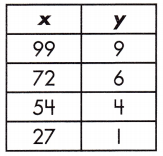
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
\(\frac{9-1}{99-27}\) = \(\frac{8}{72}\) = \(\frac{1}{9}\)
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
9 = (\(\frac{1}{9}\))(99) + b
9 = (\(\frac{1}{9}\))(99) + b
9 – 11 = 11 + b – 11
-2 = b
Step 3: Use the found values in the linear function to complete the table.
y = (\(\frac{1}{9}\))(72) – 2
y = 8 – 2 = 6
y = (\(\frac{1}{9}\))(54) – 2
y = 6 – 2 = 4

Find the relationship for each function table and then complete the table.

Question 1.
a.

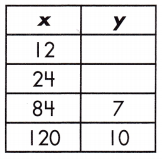
Function: _____
Answer:
1, 2, y = \(\frac{1}{12}\)x

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{10-7}{120-84}\) = \(\frac{3}{36}\) = \(\frac{1}{12}\)
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
10 = (\(\frac{1}{12}\))(120) + b
10 = (\(\frac{120}{12}\)) + b
10 – 10 =  b = 0
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = \(\frac{1}{12}\)12 + 0.
for x = 12 :: y = 1
y = \(\frac{1}{12}\)24 + 0.
for x = 24 :: y = 2
So, the relationship of the function table is y = \(\frac{1}{12}\)x
The value of y = 1, 2

b.

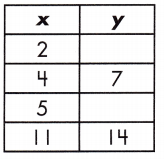
Function: _____
Answer:
5, 8, y = x + 3

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{14-7}{11- 4}\) = \(\frac{7}{7}\) = 1
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
7 = 1 (4) + b
7- 4 =  b
b = 3
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (1)2 + 3.
for x = 2 :: y = 5
y = (1)5 + 3.
for x = 5 :: y = 8
So, the relationship of function table is y = x + 3
The value of y = 5, 8

Question 2.
a.

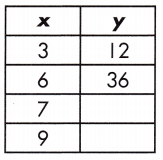
Function: _____
Answer:
44, 60, y = 10x + 10

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{36 – 12}{6 – 3}\) = \(\frac{24}{3}\) = 8
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
12 = 8 (3) + b
12 – 24 =  b
b = -12
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (8)7  – 12 = 56 – 12 = 44
for x = 7 :: y = 44
y = (8)9 – 12 = 72 – 12 = 60
for x = 9 :: y = 60
So, the relationship of the function table is y = 10x + 10
The value of y = 44, 60

b.

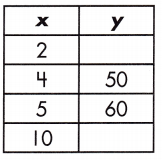
Function: _____
Answer:
30, 110, y = 10 x + 10

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{60 – 50}{5 – 4}\) = \(\frac{10}{1}\) = 10
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
50 = 10 (4) + b
50 – 40 =  b
b = 10
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (10)2  + 10 = 20 + 10 = 30
for x = 2 :: y = 80
y = (10)10 + 10 = 100 + 10 = 110
for x = 10 :: y = 100
So, the relationship of the function table is y = 10 x + 10
The value of y = 30, 110

Question 3.
a.

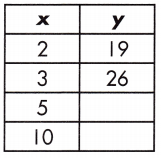
Function: _____
Answer:
40, 75, y = 7x + 5

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{26 – 19}{3 – 2}\) = \(\frac{7}{1}\) = 7
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
19 = 7 (2) + b
19 – 14 =  b
b = 5
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (7)5  + 5 = 35 + 5 = 40
for x = 5 :: y = 40
y = (7)10 + 5 = 70 + 5 = 75
for x = 10 :: y = 75
So, the relationship of the function table is y = 7x + 5
The value of y = 40, 75

b.

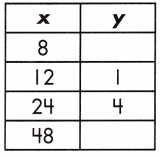
Function: _____
Answer:
0, 10, y = \(\frac{1}{4}\)x – 2

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{4 – 1}{24 – 12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
1 = \(\frac{1}{4}\) (12) + b
1 – 3 =  b
b = -2
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (\(\frac{1}{4}\))8  – 2 = 2 – 2 = 0
for x = 8 :: y = 40
y = (\(\frac{1}{4}\))48 – 2 = 12 – 2 = 10
for x = 48 :: y = 10
So, the relationship of the function table is y = \(\frac{1}{4}\)x – 2
The value of y = 0, 10

Find the relationship for each function table and then complete the table.

Question 1.
a.

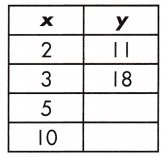
Function: _____
Answer:
32, 67, y = 7x – 3

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{18 – 11}{3 – 2}\) = \(\frac{7}{1}\) = 7
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
11 = 7 (2) + b
11 – 14 =  b
b = -3
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (7)5  – 3 = 35 – 3 = 32
for x = 5 :: y = 32
y = (7)10 – 3 = 70 – 3 = 67
for x = 10 :: y = 67
y = 7x – 3
So, the relationship of the function table is y = 7x – 3
The value of y = 32, 67

b.

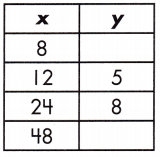
Function: _____
Answer:
4, 14, y = \(\frac{1}{4}\)x + 2

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{8 – 5}{24 – 12}\) = \(\frac{3}{12}\) = \(\frac{1}{4}\)
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
5 = \(\frac{1}{4}\) (12) + b
5 – 3 =  b
b = 2
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (\(\frac{1}{4}\))8  + 2 = 2 + 2 = 4
for x = 8 :: y = 4
y = (\(\frac{1}{4}\))48 + 2 = 12 + 2 = 14
for x = 48 :: y = 14
So, the relationship of the function is y = \(\frac{1}{4}\)x + 2
The value of y = 4, 14

Question 2.
a.

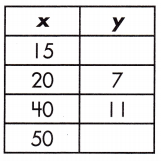
Function: _____
Answer:
6, 13, y = \(\frac{1}{5}\)x + 3

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{11 – 7}{40 – 20}\) = \(\frac{4}{20}\) = \(\frac{1}{5}\)
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
7 = \(\frac{1}{5}\) (20) + b
7 – 4 =  b
b = 3
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (\(\frac{1}{5}\))15  + 3 = 3 + 3 = 6
for x = 15 :: y = 6
y = (\(\frac{1}{5}\))50 +3 = 10 + 3 = 13
for x = 50 :: y = 13
So, the relationship of function is y = \(\frac{1}{5}\)x + 3
The value of y = 6, 13

b.

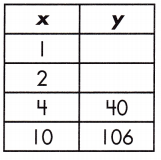
Function: _____
Answer:
7, 18, y = 11x – 4

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{106 – 40}{10 – 4}\) = \(\frac{66}{6}\) = 11
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
40 = 11 (4) + b
40 – 44 =  b
b = -4
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (11)1  – 4 = 11 – 4 = 7
for x = 1 :: y = 7
y = (11)2 – 4 = 22 – 4 = 18
for x = 10 :: y = 18
So, the relationship of the function is y = 11x – 4
The value of y = 7, 18

Question 3.
a.

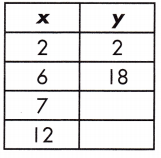
Function: _____
Answer:
22, 42, y = 4x – 6

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{18 – 2}{6 – 2}\) = \(\frac{16}{4}\) = 4
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
2 = 4 (2) + b
2 – 8 =  b
b = -6
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (4)7  – 6 = 28 – 6 = 22
for x = 7 :: y = 22
y = (4)12 – 6 = 48 – 6 = 42
for x = 12 :: y = 42
So, the relationship of the function is y = 4x – 6
The value of y = 22, 42

b.

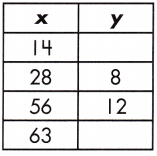
Function: _____
Answer:
6 , 13, y = \(\frac{1}{7}\)x + 4

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{12 – 8}{56 – 28}\) = \(\frac{4}{28}\) = \(\frac{1}{7}\)
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
8= \(\frac{1}{7}\) (28) + b
8= \(\frac{28}{7}\) + b
8 – 4 =  b
b = 4
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (\(\frac{1}{7}\))14  + 4 = 2 + 4 = 6
for x = 14 :: y = 6
y = (\(\frac{1}{7}\))63 + 4 = 9 + 4 = 13
for x = 63 :: y = 13
So, the relationship of the function  is y = \(\frac{1}{7}\)x + 4
The value of y = 6, 13

Question 4.
a.

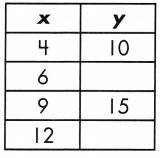
Function: _____
Answer:
12, 18, y = x + 6

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{15 – 10}{9 – 4}\) = \(\frac{5}{5}\) = 1
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
10 = 1 (4) + b
10 – 4 =  b
b = 6
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (1)6  + 6 = 6 + 6 = 12
for x = 6 :: y = 12
y = (1)12 + 6 = 12 + 6 = 18
for x = 12 :: y = 18
So, the relationship of the function is y = x + 6
The value of y = 12, 18

b.

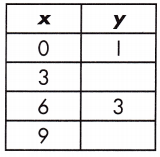
Function: _____
Answer:
2, 4, y = \(\frac{1}{3}\)x + 1

Explanation:
The table of values represents a function.
A linear relationship is in the form of y = mx + b exists.
y = mx + b
Step 1: Find the rate of change by calculating the slope, or rate of change, between the two variables.
\(\frac{y_{2}-y_{1}}{x_{2}-x_{1}}\)
m = \(\frac{3 – 1}{6 – 0}\) = \(\frac{2}{6}\) = \(\frac{1}{3}\)
Step 2: Substitute known values of x and y with the slope into the formula y = mx + b.
y = mx + b
3 = \(\frac{1}{3}\) (6) + b
3 – 2 =  b
b = 1
Step 3: Use the found values in the linear function to complete the table.
y = mx + b.
y = (\(\frac{1}{3}\))3  + 1 = 1 + 1 = 2
for x = 3 :: y = 2
y = (\(\frac{1}{3}\))9 + 1 = 3 + 1 = 4
for x = 9 :: y = 4
So, The relationship of the function is y = \(\frac{1}{3}\)x + 1
The value of y = 2, 4