Practice with the help of Spectrum Math Grade 5 Answer Key Chapter 5 Pretest regularly and improve your accuracy in solving questions.
Spectrum Math Grade 5 Chapter 5 Pretest Answers Key
Check What You Know
Write each fraction in simplest form.
Question 1.
a.
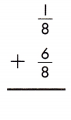
Answer: \(\frac{7}{8}\)
To add fractions with like denominators, add the numerators and use the common denominator.
\(\frac{1}{8}\) + \(\frac{6}{8}\) = \(\frac{1+6}{8}\) = \(\frac{7}{8}\)
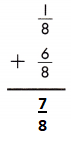
b.
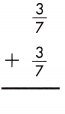
Answer: \(\frac{6}{7}\)
To add fractions with like denominators, add the numerators and use the common denominator.
\(\frac{3}{7}\) + \(\frac{3}{7}\) = \(\frac{3+3}{7}\) = \(\frac{6}{7}\)
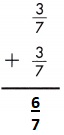
c.
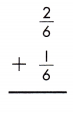
Answer: \(\frac{3}{6}\)
To add fractions with like denominators, add the numerators and use the common denominator.
\(\frac{2}{6}\) + \(\frac{1}{6}\) = \(\frac{2+1}{6}\) = \(\frac{3}{6}\)
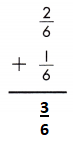
d.
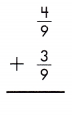
Answer: \(\frac{7}{9}\)
To add fractions with like denominators, add the numerators and use the common denominator.
\(\frac{4}{9}\) + \(\frac{3}{9}\) = \(\frac{4+3}{9}\) = \(\frac{7}{9}\)
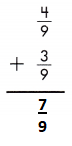
Question 2.
a.
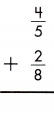
Answer: 1 \(\frac{1}{20}\)
To add fractions with like denominators, add the numerators and use the common denominator.
\(\frac{4}{5}\) + \(\frac{2}{8}\)
LCD is 40.
\(\frac{32}{40}\) + \(\frac{10}{40}\)
= \(\frac{32+10}{40}\) = \(\frac{42}{10}\) = 1 \(\frac{1}{20}\)
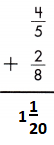
b.
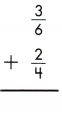
Answer: 1
\(\frac{3}{6}\) + \(\frac{2}{4}\)
LCD is 12.
\(\frac{6}{12}\) + \(\frac{6}{12}\)
= \(\frac{6+6}{12}\) = \(\frac{12}{12}\) = 1
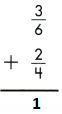
c.
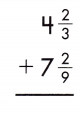
Answer: 11 \(\frac{8}{9}\)
4\(\frac{2}{3}\) + 7\(\frac{2}{9}\)
4 + \(\frac{2}{3}\) + 7 + \(\frac{2}{9}\)
4 + 7 = 11
\(\frac{2}{3}\) + \(\frac{2}{9}\)
LCD is 9.
\(\frac{6}{9}\) + \(\frac{2}{9}\) = \(\frac{8}{9}\)
11 + \(\frac{8}{9}\) = 11\(\frac{8}{9}\)
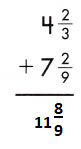
d.
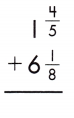
Answer: 7 \(\frac{37}{40}\)
1\(\frac{4}{5}\) + 6\(\frac{1}{8}\)
1 + \(\frac{4}{5}\) + 6 + \(\frac{1}{8}\)
1 + 6 = 7
\(\frac{4}{5}\) + \(\frac{1}{8}\)
LCD is 40.
\(\frac{32}{40}\) + \(\frac{5}{40}\) = \(\frac{37}{40}\)
7 + \(\frac{37}{40}\) = 7\(\frac{37}{40}\)
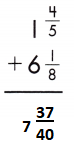
Question 3.
a.
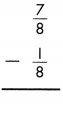
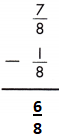
Answer:
To subtract fractions with like denominators, subtract the numerators and use the common denominator.
\(\frac{7}{8}\) – \(\frac{1}{8}\) = \(\frac{7-1}{8}\) = \(\frac{6}{8}\) = \(\frac{3}{4}\)
b.
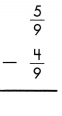
Answer:
To subtract fractions with like denominators, subtract the numerators and use the common denominator.
\(\frac{5}{9}\) – \(\frac{4}{9}\) = \(\frac{5-4}{9}\) = \(\frac{1}{9}\)
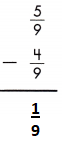
c.
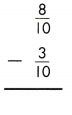
Answer:
To subtract fractions with like denominators, subtract the numerators and use the common denominator.
\(\frac{8}{10}\) – \(\frac{3}{10}\) = \(\frac{8-3}{10}\) = \(\frac{5}{10}\)
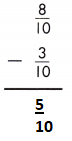
d.
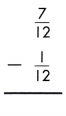
Answer:
To subtract fractions with like denominators, subtract the numerators and use the common denominator.
\(\frac{7}{12}\) – \(\frac{1}{12}\) = \(\frac{7-1}{12}\) = \(\frac{6}{12}\)
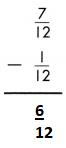
Question 4.
a.
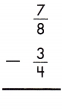
Answer: \(\frac{1}{8}\)
\(\frac{7}{8}\) – \(\frac{3}{4}\)
LCD is 8.
\(\frac{7}{8}\) – \(\frac{6}{8}\)
\(\frac{7-6}{8}\) = \(\frac{1}{8}\)
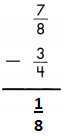
b.
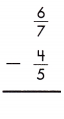
Answer: \(\frac{2}{35}\)
\(\frac{6}{7}\) – \(\frac{4}{5}\)
LCD is 35.
\(\frac{30}{35}\) – \(\frac{28}{35}\)
\(\frac{30-28}{8}\) = \(\frac{2}{35}\)
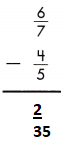
c.
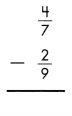
Answer: \(\frac{22}{63}\)
\(\frac{4}{7}\) – \(\frac{2}{9}\)
LCD is 63.
\(\frac{36}{63}\) – \(\frac{14}{63}\)
\(\frac{36-14}{63}\) = \(\frac{22}{63}\)
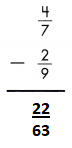
d.
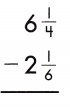
Answer: 4 \(\frac{1}{12}\)
6 \(\frac{1}{4}\) – 2\(\frac{1}{6}\)
6 + \(\frac{1}{4}\) – 2 – \(\frac{1}{6}\)
6 – 2 = 4
\(\frac{1}{4}\) – \(\frac{1}{6}\)
LCD is 12.
\(\frac{3}{12}\) – \(\frac{2}{12}\) = \(\frac{1}{12}\)
4 + \(\frac{1}{12}\) = 4\(\frac{1}{12}\)
Solve each problem. Show your work.
Question 5.
Julianne needs 7 yards of string for her kite. She has \(\frac{5}{8}\) yards. How many more yards does Julianne need for her kite?
Julianne needs _____________ more yards of string.
Answer:
Given,
Julianne needs 7 yards of string for her kite.
She has \(\frac{5}{8}\) yards.
7 – \(\frac{5}{8}\) = 6\(\frac{3}{8}\) yards
Julianne needs 6\(\frac{3}{8}\) more yards of string.
Question 6.
Mrs. Thompson’s cookie recipe includes \(\frac{1}{3}\) cup sugar and 4 cups flour. How many cups of sugar and flour does Mrs. Thompson need for her cookies?
Mrs. Thompson needs ______________ cups of ingredients.
Answer:
Given,
Mrs. Thompson’s cookie recipe includes \(\frac{1}{3}\) cup sugar and 4 cups flour.
\(\frac{1}{3}\) + 4 = 4\(\frac{1}{3}\)
Mrs. Thompson needs 4\(\frac{1}{3}\) cups of ingredients.
Question 7.
Marlon watched a movie 1\(\frac{8}{9}\) hours long. Jessie watched a movie 2\(\frac{2}{7}\) hours long. How much longer was Jessie’s movie than Marlon’s?
Jessie’s movie was _______________ hours longer.
Answer:
Given,
Marlon watched a movie 1\(\frac{8}{9}\) hours long. Jessie watched a movie 2\(\frac{2}{7}\) hours long.
2\(\frac{2}{7}\) – 1\(\frac{8}{9}\) = \(\frac{25}{63}\)
Jessie’s movie was \(\frac{25}{63}\) hours longer.
Question 8.
Carrie is running in a track meet. In one race she must run \(\frac{1}{4}\) mile, and in a second race she must run 1\(\frac{2}{5}\) miles. How many miles must Carrie run in all?
Carrie must run _____________ miles.
Answer:
Given,
Carrie is running in a track meet. In one race she must run \(\frac{1}{4}\) mile, and in a second race she must run 1\(\frac{2}{5}\) miles.
\(\frac{1}{4}\) + 1\(\frac{2}{5}\) = 1\(\frac{13}{20}\)
Carrie must run 1\(\frac{13}{20}\) miles.
Question 9.
David practiced soccer twice last week, On Monday, he practiced 2\(\frac{1}{3}\) hours. On Wednesday, he practiced 1\(\frac{7}{9}\) hours. How much longer did David practice on Monday?
David practiced _____________ hours longer on Monday.
Answer:
Given,
David practiced soccer twice last week, On Monday, he practiced 2\(\frac{1}{3}\) hours. On Wednesday, he practiced 1\(\frac{7}{9}\) hours.
2\(\frac{1}{3}\) – 1\(\frac{7}{9}\) = \(\frac{5}{9}\)
David practiced \(\frac{5}{9}\) hours longer on Monday.