This handy Spectrum Math Grade 4 Answer Key Chapter 6 Pretest provides detailed answers for the workbook questions.
Spectrum Math Grade 4 Chapter 6 Pretest Answers Key
Check What You Know
To find an equivalent fraction, multiply the fraction by the number in the circle.
Question 1.
a.
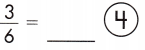
Answer:
\(\frac{12}{24}\)
Explanation:
Given,
\(\frac{3}{6}\)
To find an equivalent fraction,
multiply both the numerator and denominator by the given number 4.
\(\frac{3 × 4}{6 × 4}\) = \(\frac{12}{24}\)
So, \(\frac{3}{6}\) and \(\frac{12}{24}\) are equivalent fractions.
b.

Answer:
\(\frac{10}{15}\)
Explanation:
Given,
\(\frac{2}{3}\)
To find an equivalent fraction,
multiply both the numerator and denominator by the given number 5.
\(\frac{2 × 5}{3 × 5}\) = \(\frac{10}{15}\)
So, \(\frac{2}{3}\) and \(\frac{10}{15}\) are equivalent fractions.
c.

Answer:
\(\frac{6}{36}\)
Explanation:
Given,
\(\frac{1}{6}\)
To find an equivalent fraction,
multiply both the numerator and denominator by the given number 6.
\(\frac{1 × 6}{6 × 6}\) = \(\frac{6}{36}\)
So, \(\frac{1}{6}\) and \(\frac{6}{36}\) are equivalent fractions.
d.
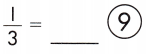
Answer:
\(\frac{9}{27}\)
Explanation:
Given,
\(\frac{1}{3}\)
To find an equivalent fraction,
multiply both the numerator and denominator by the given number 9.
\(\frac{1 × 9}{3 × 9}\) = \(\frac{9}{27}\)
So, \(\frac{1}{3}\) and \(\frac{9}{27}\) are equivalent fractions.
Draw a picture to compare the fractions. Then, write >, <, or =.
Question 2.
![]()
Answer:
\(\frac{1}{5}\) = \(\frac{2}{10}\)
Explanation:
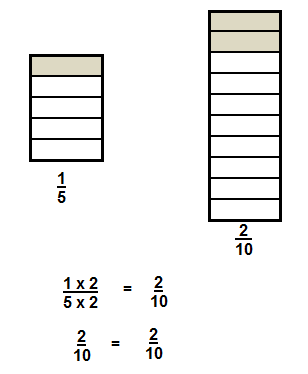
Add.
Question 3.
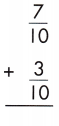
Answer:
\(\frac{10}{10}\) or 1
Explanation:
When the denominators are same, then add the numerators.
\(\frac{7}{10}\) + \(\frac{3}{10}\) = \(\frac{7+3}{10}\) = \(\frac{10}{10}\) or 1.
Write the sum over the common denominator as shown above.
Question 4.
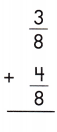
Answer:
\(\frac{7}{8}\)
Explanation:
When the denominators are same, then add the numerators.
\(\frac{3}{8}\) + \(\frac{4}{8}\) = \(\frac{3+4}{8}\) = \(\frac{7}{8}\)
Write the sum over the common denominator as shown above.
Subtract.
Question 5.
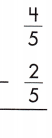
Answer:
\(\frac{2}{5}\)
Explanation:
When denominators are same, subtract the numerators.
\(\frac{4}{5}\) – \(\frac{2}{5}\) = \(\frac{4 – 2}{5}\) = \(\frac{2}{5}\)
Write the difference over the common denominator as shown above.
Question 6.
\(\frac{11}{12}\) – \(\frac{8}{12}\) = _____________
Answer:
\(\frac{3}{12}\) or \(\frac{1}{4}\)
Explanation:
When denominators are same, subtract the numerators.
\(\frac{11}{12}\) – \(\frac{8}{12}\) = \(\frac{11 – 8}{12}\)
= \(\frac{3}{12}\) or \(\frac{1}{4}\)
Write the difference over the common denominator as shown above.
Decompose the fraction.
Question 7.
\(\frac{2}{4}\)
Answer:
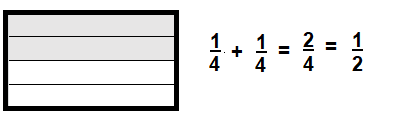
Explanation:
\(\frac{1}{4}\) + \(\frac{1}{4}\) = \(\frac{2}{4}\)
Reduce to the simplest form.
\(\frac{1}{2}\)
Write the decimal and fraction for each model.
Question 8.
![]()
__________ or ___________
Answer:
\(\frac{5}{10}\) or 0.5
Explanation:
The given model is divided into 10 parts.
Number of shaded parts = \(\frac{5}{10}\)
So, \(\frac{5}{10}\) is written as 0.5.
Question 9.

__________ or ___________
Answer:
\(\frac{44}{100}\) or 0.44
Explanation:
The given model is divided into 10 rows and columns.
Each unit in the model represent as 1.
Number of shaded parts = \(\frac{44}{100}\)
So, \(\frac{44}{100}\) is written as 0.44.
Question 10.
![]()
__________ or ___________
Answer:
\(\frac{1}{10}\) or 0.1
Explanation:
The given model is divided into 10 parts.
Number of shaded parts = \(\frac{1}{10}\)
So, \(\frac{1}{10}\) is written as 0.1.
Add or subtract.
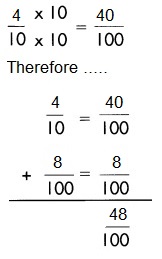
Question 11.
a.
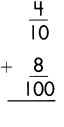
Answer:
\(\frac{48}{100}\)
Explanation:
To find the equivalent fraction for the given,
\(\frac{4}{10}\) = \(\frac{8}{100}\)
first multiple the numerator and denominator with same number to equalize the denominator.
b.
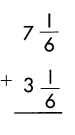
Answer:
10\(\frac{2}{6}\) or 10\(\frac{1}{3}\)
Explanation:
Add the fractions.
\(\frac{1}{6}\) + \(\frac{1}{6}\) = \(\frac{2}{6}\)
Add the whole numbers.
7 + 3 = 10
Reduce to simplest form.
\(\frac{2}{6} \div \frac{2}{2}\) = \(\frac{1}{3}\)
Hence, 10\(\frac{1}{3}\)
c.
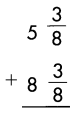
Answer:
13\(\frac{6}{8}\) or 13\(\frac{3}{4}\)
Explanation:
Add the fractions.
\(\frac{3}{8}\) + \(\frac{3}{8}\) = \(\frac{6}{8}\)
Add the whole numbers.
5 + 8 = 13
So, 13\(\frac{6}{8}\)
Reduce to simplest form.
\(\frac{6}{8} \div \frac{2}{2}\) = \(\frac{3}{4}\)
Hence, 13\(\frac{3}{4}\)
d.
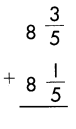
Answer:
16\(\frac{4}{5}\)
Explanation:
Add the fractions.
\(\frac{3}{5}\) + \(\frac{1}{5}\) = \(\frac{4}{5}\)
Add the whole numbers.
8 + 8 = 16
So, 16\(\frac{4}{5}\)
Question 12.
a.
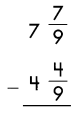
Answer:
3\(\frac{3}{9}\) or 3\(\frac{1}{3}\)
Explanation:
When denominators are same, subtract the fractions.
\(\frac{7}{9}\) – \(\frac{4}{9}\) = \(\frac{3}{9}\)
Subtract the whole numbers.
7 – 4 = 3
So, 3\(\frac{3}{9}\)
Reduce to simplest form.
3\(\frac{1}{3}\)
b.
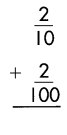
Answer:
\(\frac{22}{100}\)
Explanation:
To find the equivalent fraction for the given,
\(\frac{2}{10}\) = \(\frac{2}{100}\)
first multiple the numerator and denominator with same number to equalize the denominator.
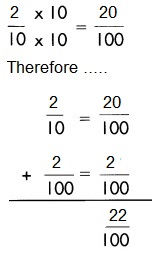
c.
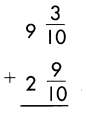
Answer:
11\(\frac{12}{10}\)
or
12\(\frac{2}{10}\)
or
12\(\frac{1}{5}\)
Explanation:
Add the fractions.
\(\frac{3}{10}\) + \(\frac{9}{10}\) = \(\frac{12}{10}\)
Add the whole numbers.
9 + 2 = 11
So, 11\(\frac{12}{10}\)
Reduce to simplest form.
12\(\frac{2}{10}\) = 12\(\frac{1}{5}\)
d.
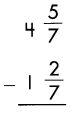
Answer:
3\(\frac{3}{7}\)
Explanation:
Subtract the numerators when denominators are same.
\(\frac{5}{7}\) – \(\frac{2}{7}\) = \(\frac{3}{7}\)
Then subtract the whole numbers.
4 – 1 = 3
So, 3\(\frac{3}{7}\)
Multiply.
Question 13.
a. \(\frac{8}{9}\) × 4 = _____________
Answer:
\(\frac{32}{9}\) or 3\(\frac{5}{9}\)
Explanation:
Given,
\(\frac{8}{9}\) × 4
= \(\frac{8}{9}\) × \(\frac{4}{1}\)
= \(\frac{8 \times 4}{9 \times 1}\)
= \(\frac{32}{7}\)
Reduce to the simplest form.
3\(\frac{5}{9}\)
b. 3 × \(\frac{1}{8}\) = ______________
Answer:
\(\frac{3}{8}\)
Explanation:
Given,
3 × \(\frac{1}{8}\)
= \(\frac{3}{1}\) × \(\frac{1}{8}\)
= \(\frac{3 \times 1}{1 \times 8}\)
= \(\frac{3}{8}\)
c. \(\frac{4}{7}\) × 2 = ______________
Answer:
\(\frac{8}{7}\) or 1\(\frac{1}{7}\)
Explanation:
Given,
\(\frac{4}{7}\) × 2
= \(\frac{4}{7}\) × \(\frac{2}{1}\)
= \(\frac{4 \times 2}{7 \times 1}\)
= \(\frac{8}{7}\)
Reduce to the simplest form.
1\(\frac{1}{7}\)
d. \(\frac{5}{7}\) × 8 = ______________
Answer:
\(\frac{40}{7}\) or 5\(\frac{5}{7}\)
Explanation:
Given,
\(\frac{5}{7}\) × 8
= \(\frac{5}{7}\) × \(\frac{8}{1}\)
= \(\frac{5 \times 8}{7 \times 1}\)
= \(\frac{40}{7}\)
Reduce to the simplest form.
5\(\frac{35}{7}\)
Question 14.
a. 5 × \(\frac{3}{10}\) = _______________
Answer:
\(\frac{15}{10}\) or \(\frac{3}{2}\)
Explanation:
Given,
5 × \(\frac{3}{10}\)
= \(\frac{5}{1}\) × \(\frac{3}{10}\)
= \(\frac{5 \times 1}{3 \times 10}\)
= \(\frac{15}{10}\)
= \(\frac{3}{2}\)
b. 2 × \(\frac{7}{12}\) = ________________
Answer:
\(\frac{14}{12}\) or 1\(\frac{1}{7}\)
Explanation:
Given,
2 × \(\frac{7}{12}\)
= \(\frac{2}{1}\) × \(\frac{7}{12}\)
= \(\frac{2 \times 1}{7 \times 12}\)
= \(\frac{14}{12}\)
Reduce to the simplest form.
1 \(\frac{1}{7}\)
c. \(\frac{6}{11}\) × 7 = ________________
Answer:
\(\frac{42}{11}\) or 3\(\frac{9}{11}\)
Explanation:
Given,
\(\frac{6}{11}\) × 7
= \(\frac{6}{11}\) × \(\frac{7}{1}\)
= \(\frac{6 \times 7}{11 \times 1}\)
= \(\frac{42}{11}\)
Reduce to the simplest form.
3\(\frac{9}{11}\)
d. \(\frac{2}{9}\) × 8 = ________________
Answer:
\(\frac{16}{9}\) or 1\(\frac{7}{9}\)
Explanation:
Given,
\(\frac{2}{9}\) × 8
= \(\frac{2}{9}\) × \(\frac{8}{1}\)
= \(\frac{2 \times 8}{9 \times 1}\)
= \(\frac{16}{9}\)
Reduce to the simplest form.
1\(\frac{7}{9}\)