This handy Spectrum Math Grade 4 Answer Key Chapter 6 Lesson 6.12 Subtracting Mixed Numerals with Like Denominators provides detailed answers for the workbook questions.
Spectrum Math Grade 4 Chapter 6 Lesson 6.12 Subtracting Mixed Numerals with Like Denominators Answers Key
\(\frac{2}{8}\) is less than \(\frac{3}{8}\). Rename 3\(\frac{3}{8}\).
Subtract the fractions.
Subtract the whole numbers.
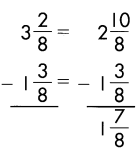
3 = 2 + 1 + \(\frac{2}{8}\)
= 2 + \(\frac{8}{8}\) + \(\frac{2}{8}\) = 2\(\frac{10}{8}\)
Subtract. Write answers in simplest form.
Question 1.
a.
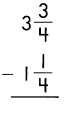
Answer:
2\(\frac{1}{2}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{3}{4}\) – \(\frac{1}{4}\) = \(\frac{2}{4}\)
Reduce to the simplest form.
\(\frac{2}{4} \div \frac{2}{2}\) = \(\frac{1}{2}\)
Then subtract the whole numbers.
3 – 1 = 2
So, 2\(\frac{1}{2}\)
b.
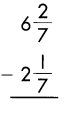
Answer:
4\(\frac{1}{7}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{2}{7}\) – \(\frac{1}{7}\) = \(\frac{1}{7}\)
Then subtract the whole numbers.
6 – 2 = 4
So, 4\(\frac{1}{7}\)
c.
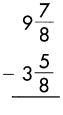
Answer:
6\(\frac{1}{4}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{7}{8}\) – \(\frac{5}{8}\) = \(\frac{2}{8}\)
Reduce to the simplest form.
\(\frac{2}{8} \div \frac{2}{2}\) = \(\frac{1}{4}\)
Then subtract the whole numbers.
9 – 3 = 6
So, 6\(\frac{1}{4}\)
d.
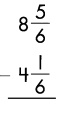
Answer:
4\(\frac{2}{3}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{5}{6}\) – \(\frac{1}{6}\) = \(\frac{4}{6}\)
Reduce to the simplest form.
\(\frac{4}{6} \div \frac{2}{2}\) = \(\frac{2}{3}\)
Then subtract the whole numbers.
8 – 4 = 4
So, 4\(\frac{2}{3}\)
e.
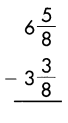
Answer:
3\(\frac{1}{4}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{5}{8}\) – \(\frac{3}{8}\) = \(\frac{2}{8}\)
Reduce to the simplest form.
\(\frac{2}{8} \div \frac{2}{2}\) = \(\frac{1}{4}\)
Then subtract the whole numbers.
6 – 3 = 3
So, 3\(\frac{1}{4}\)
Question 2.
a.
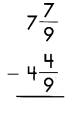
Answer:
3\(\frac{1}{3}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{7}{9}\) – \(\frac{4}{9}\) = \(\frac{3}{9}\)
Reduce to the simplest form.
\(\frac{3}{9} \div \frac{3}{3}\) = \(\frac{1}{3}\)
Then subtract the whole numbers.
7 – 4 = 3
So, 3\(\frac{1}{3}\)
b.
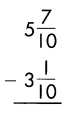
Answer:
2\(\frac{3}{5}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{7}{10}\) – \(\frac{1}{10}\) = \(\frac{6}{10}\)
Reduce to the simplest form.
\(\frac{6}{10} \div \frac{2}{2}\) = \(\frac{3}{5}\)
Then subtract the whole numbers.
5 – 3 = 2
So, 2\(\frac{3}{5}\)
c.
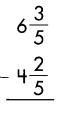
Answer:
2\(\frac{1}{5}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{3}{5}\) – \(\frac{2}{5}\) = \(\frac{1}{5}\)
Then subtract the whole numbers.
6 – 4 = 2
So, 2\(\frac{1}{5}\)
d.
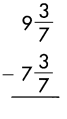
Answer:
2
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{3}{7}\) – \(\frac{3}{7}\) = 0
Then subtract the whole numbers.
9 – 7 = 2
e.
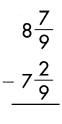
Answer:
1\(\frac{5}{9}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{7}{9}\) – \(\frac{2}{9}\) = \(\frac{5}{9}\)
Then subtract the whole numbers.
8 – 7 = 1
So, 1\(\frac{5}{9}\)
Question 3.
a.
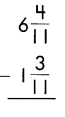
Answer:
5\(\frac{1}{11}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{4}{11}\) – \(\frac{3}{11}\) = \(\frac{1}{11}\)
Then subtract the whole numbers.
6 – 1 = 5
So, 5\(\frac{1}{11}\)
b.
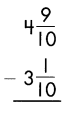
Answer:
1\(\frac{4}{5}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{9}{10}\) – \(\frac{1}{10}\) = \(\frac{8}{10}\)
Reduce to the simplest form.
\(\frac{8}{10} \div \frac{2}{2}\) = \(\frac{4}{5}\)
Then subtract the whole numbers.
4 – 3 = 1
So, 1\(\frac{4}{5}\)
c.
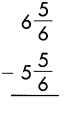
Answer:
1
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{5}{6}\) – \(\frac{5}{6}\) = 0
Then subtract the whole numbers.
6 – 5 = 1
d.
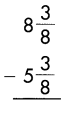
Answer:
3
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{3}{8}\) – \(\frac{3}{8}\) = 0
Then subtract the whole numbers.
8 – 5 = 3
e.
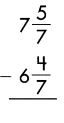
Answer:
1\(\frac{1}{7}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{5}{7}\) – \(\frac{4}{7}\) = \(\frac{1}{7}\)
Then subtract the whole numbers.
7 – 6 = 1
So, 1\(\frac{1}{7}\)
Question 4.
a.
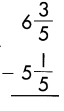
Answer:
1\(\frac{2}{5}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{3}{5}\) – \(\frac{1}{5}\) = \(\frac{2}{5}\)
Then subtract the whole numbers.
6 – 5 = 1
So, 1\(\frac{2}{5}\)
b.
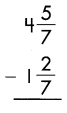
Answer:
3\(\frac{3}{7}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{5}{7}\) – \(\frac{2}{7}\) = \(\frac{3}{7}\)
Then subtract the whole numbers.
4 – 1 = 3
So, 3\(\frac{3}{7}\)
c.
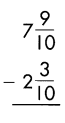
Answer:
5\(\frac{3}{5}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{9}{10}\) – \(\frac{3}{10}\) = \(\frac{6}{10}\)
Reduce to the simplest form.
\(\frac{6}{10} \div \frac{2}{2}\) = \(\frac{3}{5}\)
Then subtract the whole numbers.
7 – 2 = 5
So, 5\(\frac{3}{5}\)
d.
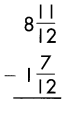
Answer:
7\(\frac{1}{3}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{11}{12}\) – \(\frac{7}{12}\) = \(\frac{5}{12}\)
Then subtract the whole numbers.
8 – 1 = 7
So, 7\(\frac{1}{3}\)
e.
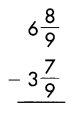
Answer:
3\(\frac{1}{9}\)
Explanation:
Subtract the numerators, when denominators of the fraction are same.
\(\frac{8}{9}\) – \(\frac{7}{9}\) = \(\frac{1}{9}\)
Then subtract the whole numbers.
6 – 3 = 3
So, 3\(\frac{1}{9}\)