Fractions expand the number system and are beyond the regular numbers such as whole numbers, integers, etc. There are several models to represent fractions visually such as linear model, area model, expressing fractions on the number line, etc. You can easily understand fractions by looking at the different representations of fractions. For a better idea, we have covered every model with examples and related pictorial representation of fractions images. Referring to them will help you become strong in the concept of how to illustrate fractions.
Do Read:
What is a Fraction?
Fraction is a mathematical way to denote a part of a whole. The Number at the bottom of the fraction is known as a denominator and the one at the top of the fraction is known as the Numerator. In general, Denominator represents the total parts and the numerator tells how many parts are there in real.
We can easily understand the fractions by visualizing them as a part of a whole or group of objects. For Example: \(\frac { 1 }{ 5 } \). In this, the denominator indicates the total number of parts is 5 and the numerator 1 indicates the parts we have.
Different Representations of Fractions
There are different types of fractions representations. All of them are pictorial ways of representing the fractions. Doing so will make it easy for you to understand the whole concept of fractions. They are namely
- Linear Model
- Area Model
Linear Model: A Popular Way to represent fractions is to use a linear model. In a linear model, we use a number line to represent the size of a fraction. In the number line length of the line is split into equal sections. The ratio of the length of the line to the total length of the line is known as a fraction. It is easy to identify equivalent fractions in the case of a linear model.
Example: Represent \(\frac { 1 }{ 3 } \) on a Number Line?
Solution:
Firstly draw a number line and split it into equal sections. We know \(\frac { 1 }{ 3 } \) lies between 0 and 1. Split into three equal parts between 0 and 1. The first part will be the fraction \(\frac { 1 }{ 3 } \), second one would be \(\frac { 2 }{ 3 } \) and third part would be \(\frac { 3 }{ 3 } \).

Area Model: It is one of the common ways to represent a fraction. In this method, we use a circle or rectangle to divide a number into equal parts. The total number of parts denotes the denominator of the fraction whereas the numerator tells how many parts need to be shaded.
These can be a great technique to visually represent the fractions and you can easily check whether they are equivalent fractions or not. We can add two fractions easily using this area model.
Example 1:
Represent the fraction \(\frac { 2 }{ 3 } \) visually?
Solution:
The below figure is the representation of fraction \(\frac { 2 }{ 3 } \). In the following figure, a total number of parts is 3 and the ones shaded are 2. Thus Numerator = 2 and Denominator = 3.

Example 2:
Four kids share a pizza among them equally. How much pizza does each kid get as a share for them?
Solution:
Total no. of kids = 4
To Share the Pizza equally each one will get a share of \(\frac { 1 }{ 4 } \).
Pictorial Representation of the above diagram is as under
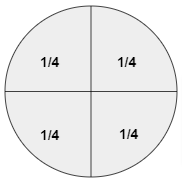
Representation of a Fraction Examples
Example 1:
Add the Fractions \(\frac { 1 }{ 2 } \) and \(\frac { 1 }{ 5 } \)
Solution:
First and foremost is to draw a pictorial representation of both the fractions.
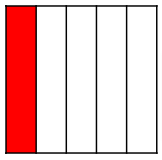
Fractional Representation of \(\frac { 1 }{ 2 } \) using area model is

Fractional Representation of \(\frac { 1 }{ 5 } \) using area model is as follows
= \(\frac { 1 }{ 2 } \) + \(\frac { 1 }{ 5 } \)
The Common Denominator between 2 and 5 is 10.
Thus, we will write the given fractions using the common denominators as such
= \(\frac { 5 }{ 10 } \) + \(\frac { 2 }{ 10 } \)
= \(\frac { 7 }{ 10 } \)

Example 2:
Represent the fraction \(\frac { 4 }{ 6 } \) on a Number Line?
Solution:
Draw a Number Line and Split it into equal parts. Since the denominator in the fraction \(\frac { 4 }{ 6 } \) is 6 we will split the number line into 6 equal parts. \(\frac { 4 }{ 6 } \) would be the 4th division marked on the number line between 0 to 1.
\(\frac { 4 }{ 6 } \) represented on the number line is as such 
