All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 9 Lesson 5 Add Unlike Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Lesson 5 Add Unlike Fractions
Math in My World
Example 1
In the morning, an octopus swam for \(\frac{1}{3}\) hour. In the afternoon, the octopus swam for \(\frac{1}{4}\) hour. For how much of one hour did the octopus swim altogether?
Find \(\frac{1}{3}\) + \(\frac{1}{4}\)
Write equivalent, like fractions using the least common denominator, LCD. The LCD of \(\frac{1}{3}\) and \(\frac{1}{4}\) is 12.
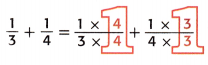
Write equivalent fractions using the LCD.
= \(\frac{4}{12}\) + \(\frac{3}{12}\) Multiply.
= \(\frac{4+3}{12}\), or 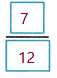
Add like fractions.
So, \(\frac{1}{3}\) + \(\frac{1}{4}\) =  The octopus swam for
The octopus swam for  hour altogether.
hour altogether.
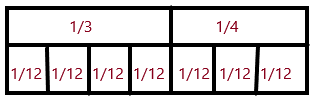
Check The model show that \(\frac{1}{3}\) + \(\frac{1}{4}\) = 
Model:
Helpful Hint
The least common denominator, LCD, is the least common multiple of the denominators.
Talk Math
How can benchmark fractions and number sense be used to check answers for reasonableness?

Answer:
benchmark fractions can be defined as common fractions that we can measure or judge against, when measuring, comparing, or ordering other fractions. Benchmark fractions are easy to visualize and identify, and thus, help in estimating the parts. When comparing two fractions with different numerators and denominators, we can either make their denominators common or compare them to a benchmark fraction such as 1/2. Benchmark fractions are most helpful when fractions to be compared are placed on a number line against the benchmarks.
Guided Practice
Add. Write each sum in simplest form.
Question 1.
\(\frac{2}{5}\) + \(\frac{1}{2}\) = 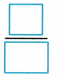
Answer:
The above-given unlike fractions:
2/5 + 1/2
step 1: Find the common denominator
10 is the least common multiple of denominators 5 and 2. Use it to convert to equivalent fractions with this common denominator.
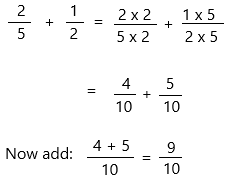
Therefore, 2/5 + 1/2 = 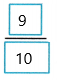
Question 2.
\(\frac{3}{4}\) + \(\frac{1}{8}\) = 
Answer:
The above-given unlike fractions:
3/4 + 1/8
Step 1: Find the common denominator.
8 is the least common multiple of denominators 4 and 8. Use it to convert to equivalent fractions with this common denominator.
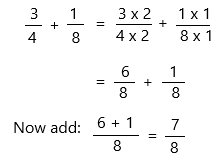
Therefore, 3/4 + 1/8 = 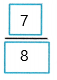
Independent Practice
Add. Write each sum in simplest form.
Question 3.
\(\frac{1}{3}\) + \(\frac{1}{5}\) = _____
Answer:
The above-given unlike fractions:
1/3 + 1/5
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
15 is the least common multiple of denominators 3 and 5. Use it to convert to equivalent fractions with this common denominator.
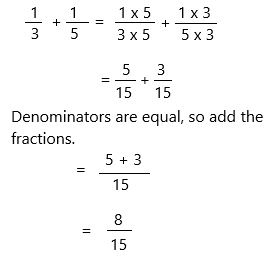
Therefore, 1/3 + 1/5 = 8/15.
Question 4.
\(\frac{1}{2}\) + \(\frac{1}{5}\) = _____
Answer:
The above-given unlike fractions:
1/2 + 1/5
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
10 is the least common multiple of denominators 2 and 5. Use it to convert to equivalent fractions with this common denominator.
1/2 + 1/5 = 1 x 5/2 x 5 + 1 x 2/5 x 2
. = 5/10 + 2/10
Here, the denominators are equal, so we can add.
. = 5 + 2/10
. = 7/10
Therefore, \(\frac{1}{2}\) + \(\frac{1}{5}\) = 7/10
Question 5.
\(\frac{5}{12}\) + \(\frac{1}{4}\) = _____
Answer:
The above-given unlike fractions:
5/12 + 1/4
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
12 is the least common multiple of denominators 12 and 4. Use it to convert to equivalent fractions with this common denominator.
5/12 + 1/4 = 5 x 1/12 x 1 + 1 x 3/4 x 3
. = 5/12 + 3/12
Here, the denominators are equal, so we can add.
. = 5 + 3/12
. = 8/12
We can reduce the fractions here.
– Reduce the fraction to the lowest terms
4 is the greatest common divisor of 8 and 12. Reduce by dividing both the numerator and denominator by 4.
8/12 = 8 ÷ 4/12 ÷ 4
. = 2/3.
Therefore, \(\frac{5}{12}\) + \(\frac{1}{4}\) = 2/3.
Question 6.
\(\frac{2}{3}\) + \(\frac{1}{6}\) = _____
Answer:
The above-given unlike fractions:
2/3 + 1/6
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
6 is the least common multiple of denominators 3 and 6. Use it to convert to equivalent fractions with this common denominator.
2/3 + 1/6 = 2 x 2/3 x 2 + 1 x 1/6 x 1
. = 4/6 + 1/6
Here the denominator is equal so that we can add them.
. = 4 + 1/6
. = 5/6
Therefore, \(\frac{2}{3}\) + \(\frac{1}{6}\) = 5/6
Question 7.
\(\frac{1}{2}\) + \(\frac{1}{4}\) = _____
Answer:
The above-given unlike fractions:
1/2 + 1/4
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
4 is the least common multiple of denominators 2 and 4. Use it to convert to equivalent fractions with this common denominator.
1/2 + 1/4 = 1 x 2/2 x 2 + 1 x 1/4 x 1
. = 2/4 + 1/4
Here the denominator is equal so that we can add them.
. = 2 + 1/4
. = 3/4
Therefore, \(\frac{1}{2}\) + \(\frac{1}{4}\) = 3/4
Question 8.
\(\frac{5}{8}\) + \(\frac{1}{16}\) = _____
Answer:
The above-given unlike fractions:
5/8 + 1/16
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
16 is the least common multiple of denominators 8 and 16. Use it to convert to equivalent fractions with this common denominator.
5/8 + 1/16 = 5 x 2/8 x 2 + 1 x 1/16 x 1
. = 10/16 + 1/16
Here the denominator is equal so that we can add them.
. = 10 + 1/16
. = 11/16
Therefore, \(\frac{5}{8}\) + \(\frac{1}{16}\) = 11/16
Question 9.
\(\frac{3}{5}\) + \(\frac{3}{10}\) = _____
Answer:
The above-given unlike fractions:
3/5 + 3/10
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
10 is the least common multiple of denominators 5 and 10. Use it to convert to equivalent fractions with this common denominator.
3/5 + 3/10 = 3 x 2/5 x 2 + 3 x 1/10 x 1
. = 6/10 + 3/10
Here the denominator is equal so that we can add them.
. = 6 + 3/10
. = 9/10
Therefore, \(\frac{3}{5}\) + \(\frac{3}{10}\) = 9/10
Question 10.
\(\frac{5}{8}\) + \(\frac{3}{16}\) = _____
Answer:
The above-given unlike fractions:
5/8 + 3/16
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
16 is the least common multiple of denominators 8 and 16. Use it to convert to equivalent fractions with this common denominator.
5/8 + 3/16 = 5 x 2/8 x 2 + 3 x 1/16 x 1
. = 10/16 + 3/16
Here the denominator is equal so that we can add them.
. = 10 + 3/16
. =13/16
Therefore, \(\frac{5}{8}\) + \(\frac{3}{16}\) = 13/16
Question 11.
\(\frac{3}{5}\) + \(\frac{3}{20}\) = _____
Answer:
The above-given unlike fractions:
3/5 + 3/20
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
20 is the least common multiple of denominators 5 and 20. Use it to convert to equivalent fractions with this common denominator.
3/5 + 3/20 = 3 x 4/5 x 4 + 3 x 1/20 x 1
. = 12/20 + 3/20
Here the denominator is equal so that we can add them.
. = 12 + 3/20
. = 15/20
– Reduce the fraction to the lowest terms
5 is the greatest common divisor of 15 and 20. Reduce by dividing both the numerator and denominator by 5.
15/20 = 15 ÷ 5/20 ÷ 5
. = 3/4
Therefore, \(\frac{3}{5}\) + \(\frac{3}{20}\) = 3/4
Algebra Find each unknown.
Question 12.
\(\frac{7}{12}\) + \(\frac{1}{3}\) = x
x = ____
Answer:
The above-given unlike fractions:
7/12 + 1/3 = x
we need to find out the value of x.
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
12 is the least common multiple of denominators 12 and 3. Use it to convert to equivalent fractions with this common denominator.
7/12 + 1/3 = 7 x 1/12 x 1 + 1 x 4/3 x 4
. = 7/12 + 4/12
Now add: (7 + 4)/12
. = 11/12
Therefore, the value of the x is 11/12.
Question 13.
\(\frac{3}{16}\) + \(\frac{3}{8}\) = \(\frac{9}{y}\)
y = ____
Answer:
The above-give unlike fractions:
3/16 + 3/8 = 9/y
we need to find out the value of y.
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
3/16 + 3/8 = 3 x 1/16 x 1 + 3 x 2/8 x 2
. = 3/16 + 6/16
Now add: (3 + 6)/16
. = 9/16
Therefore, the value of y is 16.
9 is the numerator and the denominator is 16.
Question 14.
\(\frac{3}{16}\) + \(\frac{3}{8}\) = \(\frac{9}{w}\)
w = ___
Answer:
The above-given unlike fractions:
3/16 + 3/8 = 9/w
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
3/16 + 3/8 = 3 x 1/16 x 1 + 3 x 2/8 x 2
. = 3/16 + 6/16
Now add: (3 + 6)/16
. = 9/16
Therefore, the value of w is 16.
9 is the numerator and the denominator is 16.
Problem Solving
Question 15.
A farmer harvested some of his pecan crops on Friday and Saturday. What fraction of the pecan crop was harvested in the two days?
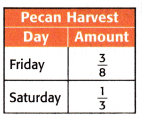
Answer:
The amount of Pecan crops harvested on Friday = 3/8
The amount of Pecan crops harvested on Saturday = 1/3
The fraction of the Pecan crop harvested in the two days = x
x = 3/8 + 1/3
First, make the denominators equal.
24 is the least common multiple of denominators 8 and 3. Use it to convert to equivalent fractions with this common denominator.
3/8 + 1/3 = 3 x 3/8 x 3 + 1 x 8/3 x 8
. x = 9/24 + 8/24
Now denominators are equal so that we can add.
. x = 9 + 8/24
. x = 17/24
Therefore, the fraction is 17/24.
Question 16.
Angel has two chores after school. She rakes leaves for \(\frac{3}{4}\) hour and spends \(\frac{1}{2}\) hour washing the car. How long does Angel spend on her chores in all?
Answer:
The above-given:
The number of hours she spends on leaves = 3/4
The number of hours she spends on washing the car = 1/2
The total hours she spends = t
t = 3/4 + 1/2
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
t = 3 x 1/4 x 1 + 1 x 2/2 x 2
t = 3/4 + 2/4
Now denominators are equal so that we can add the fractions.
t = 3 + 2/4
t = 5/4
In mixed fraction, we can write it as 1 1/4.
HOT Problems
Question 17.
Mathematical PRACTICE 2 Use Number Sense Leon found the sum of \(\frac{5}{6}\) and \(\frac{2}{3}\) to be \(\frac{11}{12}\). How can you tell that his answer is incorrect
without calculating?
Answer:
According to the above-given problem the equation is:
5/6 + 2/3 = 11/12
Here the answer is incorrect. The correct explanation is:
= 5 x 1/6 x 1 + 2 x 2/3 x 2
= 5/6 + 4/6
Here the denominators are equal so that we can add.
= ( 5 + 4)/6
= 9/6
Reduce the fraction to the lowest terms.
3 is the greatest common divisor of 9 and 6. Reduce by dividing both the numerator and denominator by 3.
9/6 = 9 ÷ 3/6 ÷ 3
. = 3/2
Convert improper fractions to mixed number
3 ÷ 2 = 1 remainder 1
The mixed number is 1 1/2.
Question 18.
Mathematical PRACTICE 2 Which One Doesn’t Belong? Circle the expression that does not belong with the other three. Explain your reasoning.
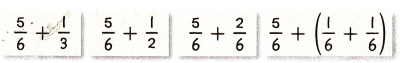
Answer:
1. 5/6 + 1/3
– Find a common denominator
6 is the least common multiple of denominators 6 and 3. Use it to convert to equivalent fractions with this common denominator.
= 5 x 1/6 x 1 + 1 x 2/3 x 2
= 5/6 + 2/6
Now add: (5 + 2)/6
= 7/6 = 1 1/6
2. 5/6 + 1/2
– Find a common denominator
6 is the least common multiple of denominators 6 and 2. Use it to convert to equivalent fractions with this common denominator.
= 5 x 1/6 x 1 + 1 x 3/2 x 3
= 5/6 + 3/6
Now add: (5 + 3)/6 = 8/6 = 4/3
3. 5/6 + 2/6 = 5 + 2/6 = 7/6 = 1 1/6.
4. 5/6 + 2/6 = 5 + 2/6 = 7/6 = 1 1/6.
5/6 + 1/2 does not belong to this group.
Question 19.
? Building on the Essential Question How are equivalent fractions used when adding, unlike fractions?
Answer:
Add and subtract fractions with unlike denominators (including mixed numbers) by replacing given fractions with equivalent fractions in such a way as to produce an equivalent sum or difference of fractions with like denominators.
McGraw Hill My Math Grade 5 Chapter 9 Lesson 5 My Homework Answer Key
Practice
Add. Write each sum in simplest form.
Question 1.
\(\frac{5}{8}\) + \(\frac{3}{10}\) = ____
Answer:
The above-given unlike fractions:
5/8 + 3/10
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
Question 2.
\(\frac{3}{5}\) + \(\frac{1}{4}\) = ____
Answer:
The above-given unlike fractions:
3/5 + 1/4
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
Question 3.
\(\frac{4}{7}\) + \(\frac{1}{8}\) = ____
Answer:
The above-given unlike fractions:
4/7 + 1/8
Here the denominators are unequal, so make them equal first.
Step 1: Make the denominators equal.
Problem Solving
Question 4.
Tashia ate \(\frac{1}{3}\) of a pizza, and Jay ate \(\frac{3}{8}\) of the same pizza. What fraction of the pizza was eaten?
Answer:
The above-given:
The amount of pizza Tashia ate = 1/3
The amount of pizza Jay ate = 3/8
The fraction of pizza eaten = e
e = 1/3 + 3/8
Find common denominator
24 is the least common multiple of denominators 3 and 8. Use it to convert to equivalent fractions with this common denominator.
e = 1 x 8/3 x 8 + 3 x 3/8 x 3
e = 8/24 + 9/24
Now add: (8 + 9)/24
e = 17/24
Therefore, the fraction is 17/24.
Question 5.
Basir took a science test on Friday. One-eighth of the questions were multiple choice, and \(\frac{3}{4}\) of the questions were true-false questions. What part of the total number of questions are either multiple-choice or true-false questions?
Answer:
The above-given:
The number of multiple questions = 1/8
The number of true-false questions = 3/4
The part of the total number of questions = q
q = 1/8 + 3/4
Find common denominator
8 is the least common multiple of denominators 8 and 4. Use it to convert to equivalent fractions with this common denominator.
q = 1 x 1/8 x 1 + 3 x 2/4 x 2
q = 1/8 + 6/8
q = 7/8
Therefore, the fraction is 7/8.
Question 6.
Mathematical PRACTICE 2 Use Number Sense Edison delivers \(\frac{1}{5}\) of the newspapers in the neighbourhood, and Anita delivers \(\frac{1}{2}\) of them. Together, Edison and Anita deliver
what fraction of the newspapers?
Answer:
The newspapers delivered by Edison = 1/5
The newspapers delivered by Anita = 1/2
Together delivered = d
d = 1/5 + 1/2
Find common denominator
10 is the least common multiple of denominators 5 and 2. Use it to convert to equivalent fractions with this common denominator.
d = 1 x 2/5 x 2 + 1 x 5/2 x 5
d = 2/10 + 5/10
d = 2 + 5/10
d = 7/10
Therefore, together delivered 7/10 newspapers.
Question 7.
Dylan and Sonia are hiking different trails. If Dylan hiked Riverwalk and Mountainview, and Sonia hiked Mountainview and Pine, how many miles did each of them hike?
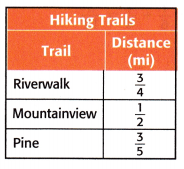
Answer:
The above-given:
The number of miles of Riverwalk = 3/4
The number of miles of Mountainview = 1/2
The number of miles of Pine = 3/5
The number of miles Dylan hiked = 3/4 + 1/2
Find common denominator
4 is the least common multiple of denominators 4 and 2. Use it to convert to equivalent fractions with this common denominator.
= 3 x 1/4 x 1 + 1 x 2/2 x 2
= 3/4 + 2/4
= 5/4 = 1 1/4
The number of miles Sonia hiked = 1/2 + 3/5
Find common denominator
10 is the least common multiple of denominators 2 and 5. Use it to convert to equivalent fractions with this common denominator.
= 1 x 5/2 x 5 + 3 x 2/5 x 2
= 5/10 + 6/10
= 11/10 = 1 1/10.
The total number of miles = t
t = 5/4 + 11/10
Find common denominator
20 is the least common multiple of denominators 4 and 10. Use it to convert to equivalent fractions with this common denominator.
t = 5 x 5/4 x 5 + 11 x 2/10 x 2
t = 25/20 + 22/20
t = 25 + 22/20
t = 47/20
– Convert improper fractions to mixed number
t = 47 ÷ 20 = 2 remainder 7
t = 2 7/20
Test Practice
Question 8.
Which expression will have the same sum as \(\frac{3}{8}\) + \(\frac{1}{4}\)?
A. \(\frac{3}{8}\) + \(\frac{1}{8}\)
B. (\(\frac{1}{8}\) + \(\frac{1}{8}\) + \(\frac{1}{8}\)) + \(\frac{1}{4}\)
C. \(\frac{3}{4}\) + \(\frac{1}{4}\)
D. (\(\frac{1}{8}\) + \(\frac{1}{8}\)) + \(\frac{1}{8}\)
Answer: Option B is correct.
The above-given:
3/8 + 1/4
The answer is 5/8
Now come to the options:
Option A: 3/8 + 1/8 = 4/8 = 1/2
Option B: (1/8 + 1/8 + 1/8) + 1/4
3/8 + 1/4 = 5/8
Option C: 3/4 + 1/4 = 4/4 = 1
Option D: 1/8 + 1/8 + 1/8 = 3/8
Therefore, the correct answer is option B.