All the solutions provided in McGraw Hill Math Grade 5 Answer Key PDF Chapter 9 Lesson 2 Add Like Fractions will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Answer Key Chapter 9 Lesson 2 Add Like Fractions
Math in My World
Example 1
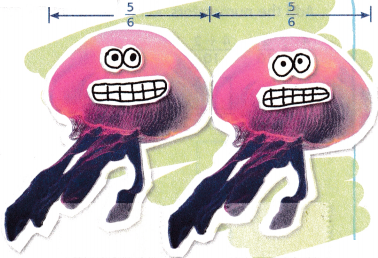
The length across the bell, or top, of a mushroom jellyfish is about \(\frac{5}{6}\) foot. If two mushroom jellyfish were placed side by side, what would be the combined length?
Find \(\frac{5}{6}\) + \(\frac{5}{6}\).
One Way Use models.
Place two sets of five \(\frac{1}{6}\) -tiles side by side.
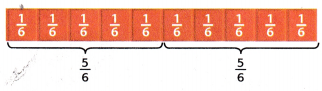
There are ___ \(\frac{1}{6}\)-tiles altogether.
.This shows the fraction \(\frac{10}{6}\), or 1\(\frac{2}{3}\).
The combined length would be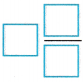 
feet.
Another Way Add the numerators. Keep the denominator.
\(\frac{5}{6}\) + \(\frac{5}{6}\) = \(\frac{5+5}{6}\)
= \(\frac{10}{6}\) 5 + 5 = 10
= 1\(\frac{2}{3}\) Write as a mixed number in simplest form.
So, \(\frac{5}{6}\) + \(\frac{5}{6}\) =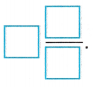 
Answer:
The above-given:
There are 2 sets of 5/6 tiles.
There are 10 1/6 tiles altogether.
The equation: 5/6 + 5/6
= 10/6 = 5/3
convert improper fractions to mixed number
5/3: 5 ÷ 3 = 1 remainder 2
The mixed number is 1 2/3.
Therefore, \(\frac{5}{6}\) + \(\frac{5}{6}\) =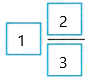 
Example 2
The table shows how much of a book Teddy read each day. What fraction of the book did Teddy read altogether on Tuesday and Thursday?
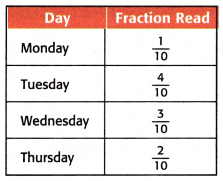
On Tuesday, Teddy read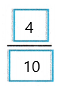 
of the book.
On Thursday, he read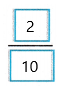 
of the book.
Add the numerators. Keep the denominator.
\(\frac{4}{10}\) + \(\frac{2}{10}\) = \(\frac{4+2}{10}\)
= 
Add. 4 + 2 = 6
= 
Write in simplest form.
So, Teddy read 
of the book on Tuesday and Thursday.
Helpful Hint
Follow these steps to simplify \(\frac{6}{10}\).
\(\frac{6}{10}\) = \(\frac{6 \div 2}{10 \div 2}\)
= \(\frac{3}{5}\)
Guided Practice
Add. Write each sum in simplest form.
Question 1.
\(\frac{1}{7}\) + .\(\frac{3}{7}\) = 
Answer:
In order to add the like fractions, there are some steps to follow. They are
1. Make sure that you have like fractions.
2. Add the numerators.
3. Write the sum over the denominator.
4. Write the answer in the simplest form.
The above-given:
1/7 + 3/7
= 1 + 3/7
= 4/7
Therefore, \(\frac{1}{7}\) + .\(\frac{3}{7}\) = 
Talk Math
Describe a real-world problem that can be solved by adding like fractions.
Answer:
a sample answer is given:
The length across the bell, or top, of a mushroom jellyfish, is about \(\frac{7}{6}\) foot. If two mushroom jellyfish were placed side by side, what would be the combined length?
The length is 7/6 + 7/6 = 14/6 = 7/3.
Question 2.
\(\frac{1}{4}\) + \(\frac{1}{4}\) = =
Answer:
The above-given:
1/4 + 1/4
Step 1: The denominators of the given numbers are the same.
Step 2: Now add the numerators without changing the denominators.
1 + 1 = 2
Step 3: Simplify the fraction if necessary.
1/4 + 1/4 = 2/4 = 1/2.
Therefore, \(\frac{1}{4}\) + \(\frac{1}{4}\) = 
Independent Practice
Add. Write each sum in simplest form.
Question 3.
\(\frac{1}{6}\) + \(\frac{1}{6}\) = ____
Answer:
The above-given:
1/6 + 1/6
Here the denominators are the same so we can add directly.
(1 + 1)/6 = 2/6 = 1/3
Therefore, \(\frac{1}{6}\) + \(\frac{1}{6}\) = 1/3.
Question 4.
\(\frac{5}{8}\) + \(\frac{3}{8}\) = ____
Answer:
The above-given like fractions:
5/8 + 3/8
Here the denominators are the same so we can add directly.
(5 + 3)/8 = 8/8 = 1
Therefore, \(\frac{5}{8}\) + \(\frac{3}{8}\) = 1.
Question 5.
\(\frac{2}{9}\) + \(\frac{3}{9}\) = ____
Answer:
The above-given:
2/9 + 3/9
Here the denominators are the same so we can add directly.
(2 + 3)/9 = 5/9
Therefore, \(\frac{2}{9}\) + \(\frac{3}{9}\) = 5/9.
Question 6.
\(\frac{4}{7}\) + \(\frac{2}{7}\) = ____
Answer:
The above-given like fractions:
4/7 + 2/7
Now add the fractions directly,
(4 + 2)/7 = 6/7
Therefore, \(\frac{4}{7}\) + \(\frac{2}{7}\) = 6/7.
Question 7.
\(\frac{2}{6}\) + \(\frac{2}{6}\) = ____
Answer:
The above-given like fractions:
2/6 + 2/6
as they were like fractions, we can add directly.
(2 + 2)/6 = 4/6 = 2/3
Therefore, \(\frac{2}{6}\) + \(\frac{2}{6}\) = 2/3.
Question 8.
\(\frac{2}{10}\) + \(\frac{5}{10}\) = ____
Answer:
The above-given:
2/10 + 5/10
as the denominators are equal, we can say that the fractions are like.
Hence, we can add directly.
(2 + 5)/10 = 7/10.
Therefore, \(\frac{2}{10}\) + \(\frac{5}{10}\) = 7/10.
Question 9.
\(\frac{3}{8}\) + \(\frac{1}{8}\) = ____
Answer:
The above-given:
3/8 + 1/8
as the denominators are equal, we can say that the fractions are like.
Hence, we can add directly.
(3 + 1)/8 = 4/8 = 1/2
Therefore, \(\frac{3}{8}\) + \(\frac{1}{8}\) = 1/2.
Question 10.
\(\frac{3}{4}\) + \(\frac{1}{4}\) = ____
Answer:
The above-given:
3/4 + 1/4
as the denominators are equal, we can say that the fractions are like.
Hence, we can add directly.
(3 + 1)/4 = 4/4 = 1
Therefore, \(\frac{3}{4}\) + \(\frac{1}{4}\) = 1
Question 11.
\(\frac{4}{9}\) + \(\frac{5}{9}\) = ____
Answer:
The above-given:
4/9 + 5/9
as the denominators are equal, we can say that the fractions are like.
Hence, we can add directly.
(4 + 5)/9 = 9/9 = 1
Therefore, \(\frac{4}{9}\) + \(\frac{5}{9}\) = 1.
Algebra Find each unknown.
Question 12.
\(\frac{1}{3}\) + 
= \(\frac{2}{3}\)
The unknown is _____
Answer:
The above-given:
1/3 + x = 2/3
we need to find out the x value.
now take ‘1/3’ to the right-hand side then the equation is:
x = 2/3 – 1/3
As the denominators are equal we can say that they are like fractions.
x = (2 – 1)/3
x = 1/3
Therefore, the unknown value is 1/3.
Question 13.
\(\frac{5}{12}\) + \(\frac{4}{12}\) = 
The unknown is _____
Answer:
The above-given:
Let the unknown value be x.
5/12 + 4/12 = x/4
(5 + 4)/12 = x/4
9/12 = x/4
4 (9/12) = x
3 = x
Therefore, the unknown value is 3.
Question 14.
\(\frac{3}{10}\) + 
= \(\frac{7}{10}\)
The unknown is _____
Answer:
The above-given:
Let the unknown value be x.
3/10 + 4/x = 7/10
Now what we do is get 3/10 on the right-hand side.
4/x = 7/10 – 3/10
4/x = (7 – 3)/10
4/x = 4/10
x = 10
Therefore, 3/10 + 4/10 = 7/10
Problem Solving
Question 15.
Terri painted \(\frac{5}{12}\) of a fence. Rey painted \(\frac{4}{12}\) of the fence. How much of the fence did they paint altogether? Write in simplest form.
Answer:
The above-given:
The fence Terrie painted = 5/12
The fence Rey painted = 4/12
The fence painted altogether = x
x = 5/12 + 4/12
x = (5 + 4)/12
x = 9/12
x = 3/4
Therefore, they painted a 3/4 of a fence.
Question 16.
Meagan walked \(\frac{4}{10}\) mile to the park. She walked the same distance home How much did she walk altogether? Write in simplest form.
Answer:
The above-given:
The number of miles Meagan walked = 4/10
The number of miles she walked home from the park = 4/10 (same distance)
The total number of miles walked = x
x = 4/10 + 4/10
x = (4 + 4)/10
x = 8/10
x = 4/5
Therefore, she walked 4/5 miles.
Question 17.
Mathematical PRACTICE 2 Use Number Sense It rained \(\frac{2}{8}\) inch in one hour. It rained \(\frac{4}{8}\) inch in the next hour Find the total amount of rain Write in simplest form.
Answer:
The above-given:
The number of inches rained in one hour = 2/8
The number of inches rained in the next hour = 4/8
The total amount of rain = x
x = 2/8 + 4/8
x = (2 + 4)/8
x = 6/8
x = 3/4
Therefore, 3/4 inches rained.
HOT Problems
Question 18.
Mathematical PRACTICE 3 Justify Conclusions Select two fractions whose sum is \(\frac{3}{4}\) and whose denominators are both the same, but not equal to 4. Justify your selection
Answer:
A sample answer is given:
If we take 8/16 and 4/16
Now add:
8/16 + 4/16
= (8 + 4)/16
= 12/16
= 3/4
(or)
we can take 3/12 and 6/12
3/12 + 6/12
= (3 + 6)/12
= 9/12
= 3/4
Question 19.
? Building on the Essential Question How are equivalent fractions used in writing a sum of two like fractions in simplest form?
Answer:
Equivalent fractions represent the same amount of distance or points on a number line. All equivalent fractions reduce to the same fraction in their simplest form.
To add like fractions, the denominators should be equal.
– The numerator represents the number of parts. The denominator represents the number of parts in a whole. I am finding the total number of the same size parts when I add the like fractions. Equivalent fractions are used to write the sum in the simplest form.
McGraw Hill My Math Grade 5 Chapter 9 Lesson 2 My Homework Answer Key
Practice
Add. Write each sum in simplest form.
Question 1.
\(\frac{7}{10}\) + \(\frac{2}{10}\) = ____
Answer:
The above-given:
7/10 + 2/10
– Here the denominators are equal, so we can add directly.
= ( 7 + 2 )/10
= 9/10
Therefore, 7/10 + 2/10 = 9/10
Question 2.
\(\frac{13}{16}\) + \(\frac{2}{16}\) = ____
Answer:
The above-given:
13/16 + 2/16
Here the denominators are equal, so we can add directly.
13 + 2/16
= 15/16
Therefore, \(\frac{13}{16}\) + \(\frac{2}{16}\) = 15/16
Question 3.
\(\frac{4}{5}\) + \(\frac{1}{5}\) = ____
Answer:
The above-given:
4/5 + 1/5
Here the denominators are equal, so we can add directly.
( 4 + 1 )/5
= 5/5
= 1
Therefore, \(\frac{4}{5}\) + \(\frac{1}{5}\) = 1.
Question 4.
\(\frac{7}{15}\) + \(\frac{2}{15}\) = ____
Answer:
The above-given:
7/15 + 2/15
Here the denominators are equal, so we can add directly.
(7 + 12)/15
= 19/15
Therefore, \(\frac{7}{15}\) + \(\frac{2}{15}\) = 19/15
Question 5.
\(\frac{9}{20}\) + \(\frac{3}{20}\) = ____
Answer:
The above-given:
9/20 + 3/20
Here the denominators are the same so we can add directly.
(9 + 3)/20
= 12/20
= 3/5
Therefore, \(\frac{9}{20}\) + \(\frac{3}{20}\) = 3/5
Question 6.
\(\frac{5}{8}\) + \(\frac{1}{8}\) = ____
Answer:
The above-given:
5/8 + 1/8
Here the denominators are equal so we can add directly.
( 5 + 1)/8
= 6/8
= 3/4
Therefore, \(\frac{5}{8}\) + \(\frac{1}{8}\) = 3/4.
Problem Solving
The table gives the fraction of each type of parade float used in a recent parade. Use the table to answer Parade Float used in a recent parade. Use the table to answer Exercises 7 and 8.
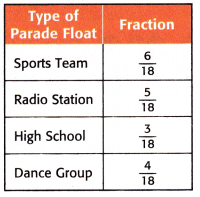
Question 7.
What fraction of the floats were from either a dance group or a radio station? Write in simplest form.
________________
Answer:
The dance group = 4/18
The radio station = 5/18
The fraction of both = 4/18 + 5/18
= (4 + 5)/18
= 9/18
= 1/2
Therefore, the fraction is 1/2.
Question 8.
What fraction of the floats were not from a sports team? Write in simplest form.
Answer:
The dance group = 4/18
The radio station = 5/18
The high school = 3/18
The fraction of the floats were not from a sports team = x
x = 4/18 + 5/18 + 3/18
x = (4 + 5 + 3)/18
x = 12/18
x = 2/3
Question 9.
Mathematical PRACTICE 3 Draw a Conclusion Sherry was in charge of distributing 25 food items that were donated to the local food pantry. On Monday, she distributed 8 items. On Tuesday, she distributed 7 items. Five more items were distributed on Wednesday. What fraction of the food items were distributed by the end of the day on Wednesday?
Answer:
The total number of food items distributed = 25
The number of items she distributed on Monday = 8
The number of items she distributed on Tuesday = 7
The number of items she distributed on Wednesday = 5
The fraction of the food items were distributed by the end on Wednesday = x
x = 8/25 + 7/25 + 5/25
x = (8 + 7 + 5)/25
x = 20/25
x = 4/5
Therefore, she distributed 4/5 food items.
Vocabulary Check
Complete the sentence with the correct vocabulary word(s).
Question 10.
Both fractions in the expression \(\frac{1}{3}\) + \(\frac{1}{3}\) are examples of ________________
Answer:
1/3 + 1/3 are the like fractions.
The group of two or more fractions that have exactly the same denominator are called like fractions. Or we can say that the fractions which have the same numbers in the denominators are called like fractions. For example, 1/7, 2/7, 5/7, 6/7 are all like fractions, whose denominators equal to 7.
Test Practice
Question 11.
Gina is working on a jigsaw puzzle. She completed \(\frac{1}{10}\) of the puzzle yesterday and \(\frac{3}{10}\) of the puzzle today. In the simplest form, what fraction of the puzzle is completed?
A. \(\frac{2}{5}\)
B. \(\frac{3}{5}\)
C. \(\frac{2}{10}\)
D. \(\frac{3}{10}\)
Answer: Option A is the correct answer.
Explanation:
The above-given:
1/10 + 3/10
(1 + 3)/10
= 4/10
= 2/5
Therefore, the fraction is 2/5.