All the solutions provided in McGraw Hill My Math Grade 5 Answer Key PDF Chapter 9 Check My Progress will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 5 Chapter 9 Check My Progress Answer Key
Check My Progress Page No. 643-644
Vocabulary Check
Write the vocabulary words that describe each set of fractions below.
like fractions unlike fractions
Question 1.
\(\frac{1}{2}\) and \(\frac{1}{3}\) _____
Answer:
The above-given fractions: 1/2 and 1/3
both are unequal. So we can that both fractions are unlike fractions.
Definition of unlike fractions: Fractions with different denominators are called, unlike fractions. Here the denominators of fractions have different values. For example, 2/3, 4/9, 6/67, and 9/89 are unlike fractions.
Question 2.
\(\frac{2}{9}\) and \(\frac{2}{9}\) _____
Answer:
The above-given fractions: 2/9 and 2/9
The given fractions are equal. So we can say they are like fractions.
Definition of like fractions: The group of two or more fractions that have exactly the same denominator are called like fractions. Or we can say that the fractions which have the same numbers in the denominators are called like fractions.
Concept Check
Round each fraction to 0, \(\frac{1}{2}\), or 1. Use a number line if needed.
Question 3.
\(\frac{9}{16}\) ≈ _____
Answer: 1/2
Explanation:
The above-given fraction: 9/16
we have to round to 0, 1/2 or 1.
so we take the numerator 9 as 8. Now the fraction will be 8/16.
8/16 = 1/2.
Therefore, we rounded the fraction to 1/2.
Question 4.
\(\frac{12}{15}\) ≈ _____
Answer: 1
Explanation:
The above-given fraction: 12/15
we round numerator 12 as 15.
Now the fraction will be 15/15
15/15 = 1
Therefore, we round the fraction to 1.
Question 5.
\(\frac{1}{10}\) ≈ _____
Answer: 0
Explanation:
The above-given fraction: 1/10
a unit fraction is given above.
1/10 = 0.1
We can round the fraction to 0.
Add. Write each sum in simplest form.
Question 6.
\(\frac{5}{9}\) + \(\frac{1}{9}\) = _____
Answer:
The above-given fraction:
5/9 + 1/9
Here the denominator is equal in both fractions.
Take LCM directly ‘9’.
= 5 + 1 / 9
= 6/9
Here we can divide by 3
6 ÷ 3 / 9 ÷ 3
= 2/3.
Therefore, 5/9 + 1/9 = 2/3.
Question 7.
\(\frac{1}{7}\) + \(\frac{6}{7}\) = _____
Answer:
The above-given fractions: 1/7 + 6/7
The denominator is equal for both fractions.
We can take LCM directly ‘7’.
1 + 6/7
= 7/7
= 1
Therefore, 1/7 + 6/7 = 1.
Question 8.
\(\frac{7}{16}\) + \(\frac{3}{16}\) = _____
Answer:
The above-given fractions: 7/16 + 3/16
The denominator is equal in both fractions.
We can take LCM directly ’16’.
7 + 3 / 16
= 10/16
Here we can definitely divide by 2.
10 ÷ 2 / 16 ÷ 2
= 5/8
Therefore, 7/16 + 3/16 = 5/8.
Question 9.
\(\frac{1}{6}\) + \(\frac{7}{12}\) = _____
Answer:
The above-given fractions:
1/6 + 7 /12
Here the denominators are not equal in both fractions.
We have to find the common denominator.
12 is the least common multiple of denominators 6 and 12. Use it to convert to equivalent fractions with this common denominator.
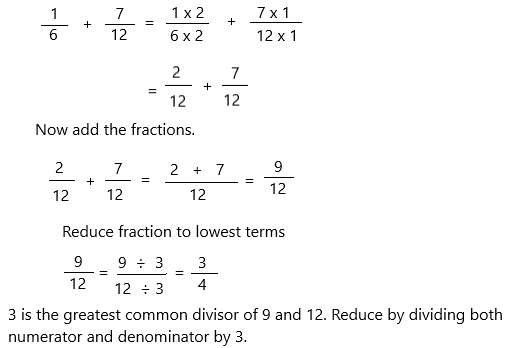
Therefore, 1/6 + 7 /12 = 3/4.
Question 10.
\(\frac{1}{8}\) + \(\frac{3}{4}\) = _____
Answer:
The above-given fractions:
1/8 + 3/4
Here, the denominators are not equal in both fractions. So we have to find out the common denominator.
– 8 is the least common multiple of denominators 8 and 4. Use it to convert to equivalent fractions with this common denominator.
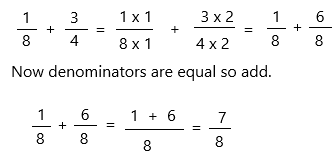
Therefore, 1/8 + 3/4 = 7/8
Question 11.
\(\frac{1}{4}\) + \(\frac{3}{8}\) = _____
Answer:
The above-given fractions:
1/4 + 3/8
Here, the denominators are not equal in both fractions. So we have to find out the common denominator.
– 8 is the least common multiple of denominators 8 and 4. Use it to convert to equivalent fractions with this common denominator.
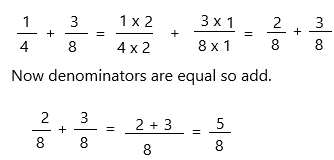
Subtract. Write each difference in simplest form.
Question 12.
\(\frac{4}{5}\) – \(\frac{1}{5}\) = _____
Answer:
The above-given fractions:
4/5 – 1/5
Here the denominators are equal. So we can subtract directly by taking the lcm as 5.
4 – 1 / 5 = 3 / 5.
Therefore, 4/5 – 1/5 = 3/5.
Question 13.
\(\frac{11}{20}\) – \(\frac{7}{20}\) = _____
Answer:
The above-given fractions:
11/20 – 7/20
Here the denominators are equal. So we can subtract directly by taking the lcm as 20.
11 – 7 / 20
= 4/20
Here we can definitely divide by 4
= 4 ÷ 4 / 20 ÷ 4
= 1/5
Question 14.
\(\frac{9}{16}\) – \(\frac{7}{16}\) = _____
Answer:
The above-given fractions:
9/16 – 7/16
Here the denominators are equal. So we can subtract directly by taking the lcm as 16.
9 – 7 / 16
= 2 / 16
Here, we can definitely divide by 2.
= 2 ÷ 2 / 16 ÷ 2
= 1 / 8
Question 15.
Mike spent \(\frac{11}{12}\) hour talking on his cell phone. Brent spent \(\frac{7}{12}\) hour talking on his cell phone. How much more time did Mike spend on his cell phone than Brent?
Answer:
The time Mike spent talking on his cell phone = 11/12
The time Brent spent talking on his cell phone = 7/12
The more time Mike spends on his cell phone than Brent. Let it be X.
X = the time mike spent – the time Brent spent
X = 11/12 – 7/12
X = 4 / 12
If we divide by 4 we get the:
X = 4/12 = 4 ÷ 4 / 12 ÷ 4
X = 1/3
Therefore, Mike spent 1/3rd of the time spent more than Brent.
Question 16.
Christie decided to make bracelets for the fifth-grade class girls. Two-fifths of the bracelets were finished on Monday, and \(\frac{3}{7}\) of the bracelets were finished on Tuesday. What part of the total number of bracelets are finished?
Answer:
The above-given:
The bracelets finished on Monday = 2/5
The bracelets finished on Tuesday = 3/7
The part of total number of bracelets is finished. Let it be A
A = bracelets finished on Monday + bracelets finished on Tuesday
A = 2/5 + 3/7
Here, find the common denominator.
– 35 is the least common multiple of denominators 5 and 7. Use it to convert to equivalent fractions with this common denominator.
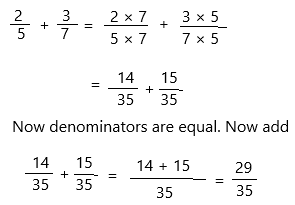
The part of a total number of bracelets is 29/35.
Question 17.
Jamila ate \(\frac{3}{8}\) of a salad. Manny ate \(\frac{2}{8}\) of the same salad. How much salad did they eat altogether?

Answer:
The amount of salad Jamila ate = 3/8
The amount of salad Manny ate = 2/8
The amount of salad they eat together. Let it be X.
X = 3 / 8 + 2 / 8
X = 3 + 2 / 8
X = 5 / 8.
therefore, 5/8 of the salad they ate together.
Test Practice
Question 18.
The table shows the fraction of a book Karen read Saturday and Sunday. What fraction of her book did she read on these two days?
A. \(\frac{3}{8}\)
B. \(\frac{1}{2}\)
C. \(\frac{8}{15}\)
D. \(\frac{11}{15}\)
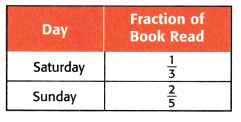
Answer: Option D is correct.
The above-given fractions: 1/3 and 2/5
The fraction of books Karen read Saturday and Sunday = 1/3 + 2/5
Now simplify the fraction:
The denominators are not equal so make the denominators equal.
– Find the common denominator:
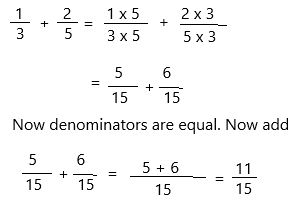
Check My Progress Page No. 669-670
Vocabulary Check
Use the word bank below to complete each sentence.
benchmark fractions denominator least common denominator (LCD)
mixed number numerator unknown
Question 1.
The _____ is the bottom number in a fraction.
Answer: denominator.
Definition: A denominator is the bottom part of a fraction. When an integer is expressed as a fraction, then there appear two numbers separated by a horizontal line. The denominator is the number that appears at the bottom of the horizontal line, whereas the number above the line is the numerator. The denominator represents the number of parts an object or an item is divided into.
Question 2.
A number that has a whole number part and a fraction part is a _____
Answer: Mixed number.
It represents a number greater than or equal to one. Numbers that are not whole numbers, but are greater than one, can be written as improper fractions or mixed numbers. A mixed number has a whole number part and a fraction part.
Question 3.
A missing value in a number sentence or equation is the _____
Answer: Variable.
– A variable is a value in an expression that can change or vary. However, when there is only one variable in an equation then the value of that variable can be calculated e.g. a + 6 = 9, 20 = 4b.
Question 4.
The ____ is the top number in a fraction.
Answer: numerator
A numerator is the part of a fraction above the line, which signifies the number to be divided by another number below the line. In the example given below, the number that lies above the line is the numerator, i.e. in the fraction 1/8, 1 represents the numerator, and 8 represents the denominator.
Concept Check
Subtract. Write the difference in simplest form.
Question 5.
\(\frac{7}{10}\) – \(\frac{1}{2}\) = _____
Answer: 1/5
Explanation:
The above-given fraction:
7/10 – 1/2
The denominator is not equal in both fractions so make the denominators equal.
– Find the common denominator:
* 10 is the least common multiple of denominators 10 and 2. Use it to convert to equivalent fractions with this common denominator.
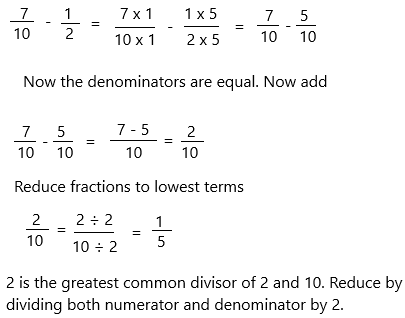
Question 6.
\(\frac{5}{8}\) – \(\frac{1}{6}\) = _____
Answer: 11/24
Explanation:
The above-given fractions:
5/8 – 1/6
The denominator is not equal in both fractions so make the denominators equal.
– Find the common denominator:
* 24 is the least common multiple of denominators 8 and 6. Use it to convert to equivalent fractions with this common denominator.
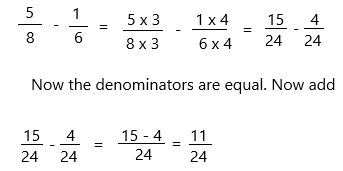
Question 7.
\(\frac{7}{12}\) – \(\frac{1}{3}\) = _____
Answer: 1/4
Explanation:
The above-given fractions:
7/12 – 1/3
The denominator is not equal in both fractions so make the denominators equal.
– Find the common denominator:
* 12 is the least common multiple of denominators 12 and 3. Use it to convert to equivalent fractions with this common denominator.
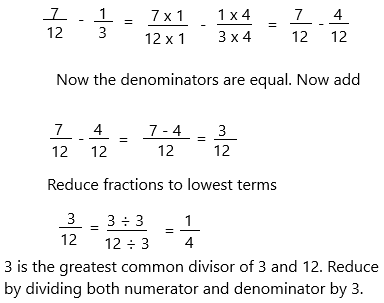
The estimate is by rounding each mixed number to the nearest whole number.
Question 8.
8\(\frac{9}{15}\) – \(\frac{4}{5}\)
Answer:
The above-given fractions:
8 9 /15 – 4/5
Here we rounded 9/15 to 1
8 + 1 = 9
Now the other fraction 4/5 is rounded to 1.
4/5 = 0.8 which is nearest to 1 so we rounded it to 1.
9 – 1 = 8
Therefore, the whole number is 8.
Question 9.
\(\frac{9}{16}\) + 16\(\frac{5}{8}\)
Answer:
The above-given fractions:
9/16 + 16 5/8
Here we rounded 9/16 to 1.
5/8 also rounded to 1.
16 + 1 = 17
Now add both numbers.
1 + 17 = 18
Therefore, the whole number is 18.
Question 10.
5\(\frac{6}{11}\) – 3\(\frac{4}{5}\)
Answer:
The above-given fractions:
5 6 / 11 – 3 4/5
11 ÷ 2 = 5 1/2
6 > 5 1/2
Here we rounded up the fraction to 6.
4/5 rounded up the 1
3 + 1 = 4
Now subtract both numbers.
6 – 4 = 2
Therefore, the whole number is 2.
Problem Solving
Question 11.
The table shows how many hours Allie swam in two weeks. For about how many hours did she swim altogether? Round each mixed number to the nearest whole number.
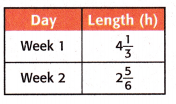
Answer:
The above-given fractions:
The length in week 1 = 4 1/3
The length in week 2 = 2 5/6
The number of hours she swims altogether. Let it be X.
X = 4 1/3 + 2 5/6
Now round the mixed number to the nearest whole number
1/3 is rounded to 0.
4 + 0 = 4
5/6 rounded to 1
2 + 1 = 3
Now add the numbers.
X = 4 + 3
X = 7
Therefore, she swims 7 hours altogether.
Question 12.
To clean a large painting, you need 3\(\frac{1}{4}\) ounces of cleaner. A small painting requires only 2\(\frac{3}{4}\) ounces. You have 8 ounces of cleaner. About how many ounces of cleaner will you have left if you clean a large and a small painting? Round each mixed number to the nearest whole number.
Answer:
The above-given:
The number of ounces of cleaner needs to clean a large painting = 3 1/4
The number of ounces of cleaner needs to clean a small painting = 2 3/4
The number of already have = 8
The equation is 8 – 3 1/4 + 2 3/4
1/4 is rounded to 0. { 3 + 0 = 3}
3/4 is rounded to 1. { 2 + 1 = 3}
Now substitute the numbers in the equation.
Left = 8 – 3 + 3
Left = 8 – 6
Left = 2
Therefore, after cleaning small and large paintings they are left with 2 ounces of cleaner.
Question 13.
Andrew plays football. On one play, he ran the ball 24\(\frac{1}{3}\)– yards. The following play, he was tackled and lost 3\(\frac{2}{3}\) yards. The next play, he ran for 5\(\frac{1}{4}\) yards. Estimate how much farther the ball is down the field after these three plays. Round each mixed number to the nearest whole number.
Answer:
The above-given:
The number of yards he ran on one play = 24 1/3
The number of yards he lost = 3 2/3
The number of yards he ran on the second play = 5 1/4
After three plays. Let it be X.
24 1/3 – 3 2/3
1/3 rounded to 0 {24 + 0 = 0}
2/3 is rounded to 1 { 3 + 1 = 4}
So, 24 – 4 = 20
For the next play: 20 + 5 1/4
1/4 is rounded to 0 { 5 + 0 = 5}
X = 20 + 5 = 25
Therefore, about 25 yards the ball is down the field
Question 14.
Marsha and Tegene are making table decorations for a party. Marsha made \(\frac{2}{9}\) of decoration in half an hour. Tegene made \(\frac{2}{3}\) of decoration in the same amount of time. How much more of a decoration did Tegene make in half an hour?
Answer:
The above-given:
The time taken by Marsha to decorate = 2/9
The time taken by Tegene to decorate = 2/3
The more time decoration Tegene makes in half an hour. Let it be X.
X = 2/3 – 2/9
Here find the common denominator:
2/3 – 2/9 = 2 x 3/3 x 3 – 2 x 1/9 x 1 = 6/9 – 2/9
6 – 2/9 = 4/9
Therefore, 4/9 more time he had taken.
Test Practice
Question 15.
Greta’s family drinks 3\(\frac{1}{4}\) quarts of milk and 1\(\frac{5}{6}\) quarts of juice in one week. About how much more milk than juice does Greta’s family drink in one week?
A. \(\frac{1}{2}\) quart
B. 1 quart
C. 2 quarts
D. 3 quarts
Answer: Option B is the correct answer.
The number of quarts of milk Greta’s family drinks = 3 1/4
The number of quarts of juice Greta’s family drinks = 1 5/6
The number of quarts of more milk than juice Greta’s family drinks in one week. Let it be X.
X = 3 1/4 – 1 5/6
1/4 rounded to 0 { 3 + 0 = 3}
5/6 rounded to 1 { 1 + 1 = 2}
X = 3 – 2
X = 1
Therefore, the Greats family drinks 1 quart of more milk than juice in one week.