All the solutions provided in McGraw Hill My Math Grade 4 Answer Key PDF Chapter 7 Lesson 8 Equations with Two Operations will give you a clear idea of the concepts.
McGraw-Hill My Math Grade 4 Answer Key Chapter 7 Lesson 8 Equations with Two Operations
Sometimes an equation has more than one operation.
Build It
Model the equation (n × 3) + 5 = y.

1. Set up an equation machine.
Use paper plates to represent the variables, rubber bands for parentheses, paper clips for the equals sign, and index cards to show the numbers and operations.
2. Input counters to find y.
Suppose n equals 1. Place 1 counter on the plate labeled n. Move the counters through the machine, following the operations given. Use the order of operations.
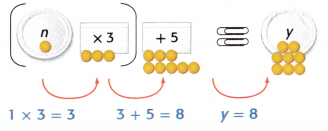
3. Record the equation.
Fold a piece of paper in half and label it as shown.
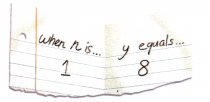
So, when n = 1, y = ______________.
Answer:
Equation: (n × 3) + 5 = y.
So, when n = 1, y = 8.
Explanation:
Equation:
(n × 3) + 5 = y.
When n = 1;
(1 × 3) + 5
=> 3 + 5
=> 8 = y.
Try It
Input more values for the equation (n × 3) + 5 = y. Find new input and output values.
Suppose n equals 2. Find the value of y.
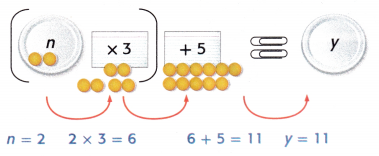
So, when n = 2, y = _______________.
Repeat the process for input values of 3, 4, and 5. Record your input (n) and output (y) values.

Answer:

Explanation:
Equation:
(n × 3) + 5 = y.
When n = 2;
y = (2 × 3) + 5
y = 6 + 5
y = 11.
When n = 3;
y = (3 × 3) + 5
y = 9 + 5
y = 14.
When n = 4;
y = (4 × 3) + 5
y = 12 + 5
y = 17.
When n = 5;
y = (5 × 3) + 5
y = 15 + 5
y = 20.
Talk About It
Question 1.
Mathematical PRACTICE Use Algebra Refer to the equation (n × 3) + 5 = y. What is the value of y when n equals 6? 7?
Answer:
23 and 26 are the value of y when n equals 6? 7?
Explanation:
Equation (n × 3) + 5 = y.
When n = 6;
y = (6 × 3) + 5
y = 18 + 5
y = 23.
When n = 7;
y = (7 × 3) + 5
y = 21 + 5
y = 26.
Question 2.
Given the equation (n + 7) × 3 = y, how would you find the value of y if n equals 3?

Answer:
30 is the value of y if n equals 3.
Explanation:
Equation: (n + 7) × 3 = y.
When n = 3;
y = (n + 7) × 3
y = (3 + 7) × 3
y = 10 × 3
y = 30.
Practice It
Use each equation to find each unknown. Use models if needed.
Question 3.
(t + 8) × 2 = s
When t = 4, s = ___________.
Answer:
(t + 8) × 2 = s
When t = 4, s = 24.
Explanation:
(t + 8) × 2 = s
When t = 4, s = ??
s = (t + 8) × 2
s = (4 + 8) × 2
s = 12 × 2
s = 24.
Question 4.
(m × 6) + 4 = d
When m = 3, d = ___________.
Answer:
(m × 6) + 4 = d
When m = 3, d = 22.
Explanation:
(m × 6) + 4 = d
When m = 3,
d = (m × 6) + 4
d = (3 × 6) + 4
d = 18 + 4
d = 22.
Question 5.
8 + (z × 2) = w
When z = 5, w = ___________.
Answer:
8 + (z × 2) = w
When z = 5, w = 18.
Explanation:
8 + (z × 2) = w
When z = 5,
w = 8 + (z × 2)
w = 8 + (5 × 2)
w = 8 + 10
w = 18.
Question 6.
(a ÷ 6) + 5 = b
When a = 18, b = ___________.
Answer:
(a ÷ 6) + 5 = b
When a = 18, b = 8.
Explanation:
(a ÷ 6) + 5 = b
When a = 18,
b = (a ÷ 6) + 5
b = (18 ÷ 6) + 5
b = 3 + 5
b = 8.
Question 7.
12 – (e × 4) = f
When e = 2, f = ___________.
Answer:
12 – (e × 4) = f
When e = 2, f = 4.
Explanation:
12 – (e × 4) = f
When e = 2,
f = 12 – (e × 4)
f = 12 – (2 × 4)
f = 12 – 8
f = 4.
Question 8.
(r + 8) × 6 = s
When r = 3, s = ___________.
Answer:
(r + 8) × 6 = s
When r = 3, s = 66.
Explanation:
(r + 8) × 6 = s
When r = 3,
s = (r + 8) × 6
s = (3 + 8) × 6
s = 11 × 6
s = 66.
Question 9.
(g – 4) × 7 = h
When g = 12, h = ___________.
Answer:
(g – 4) × 7 = h
When g = 12, h = 56.
Explanation:
(g – 4) × 7 = h
When g = 12,
h = (g – 4) × 7
h = (12 – 4) × 7
h = 8 × 7
h = 56.
Question 10.
64 ÷ (p + 4) = q
When p = 4, q = _____________.
Answer:
64 ÷ (p + 4) = q
When p = 4, q = 64.
Explanation:
64 ÷ (p + 4) = q
When p = 4,
q = 64 ÷ (p + 4)
q = 64 ÷ (4 + 4)
q = 64 ÷ 1
q = 64.
Apply It
Question 11.
Set up an equation machine to show (x + 4) ÷ 3 = y. Find the values of y when x = 8, x = 11, and x = 20.
When x = 8, y = _____________.
When x = 11, y = _____________.
When x = 20, y = _____________.
Answer:
Equation:
(x + 4) ÷ 3 = y.
When x = 8, y = 4.
When x = 11, y = 5.
When x = 20, y = 6.
Explanation:
Equation:
(x + 4) ÷ 3 = y.
When x = 8,
y = (x + 4) ÷ 3
y = (8 + 4) ÷ 3
y = 12 ÷ 3
y = 4.
When x = 11,
y = (x + 4) ÷ 3
y = (11 + 4) ÷ 3
y = 15 ÷ 3
y = 5.
When x = 20,
y = (x + 4) ÷ 3
y = (20 + 4) ÷ 3
y = 24 ÷ 3
y = 6.
Question 12.
Mathematical PRACTICE Find the Error Robert is finding the output values for the equation a + 7 × 3 = b. He wrote a few statements about the input and output values.
When a = 3, b = 30.
When a = 4, b = 33.
When a = 5, b = 36.
What is Robert’s mistake?
_____________________
Use the equation correctly to find the output values.
When a = 3, b = ______________.
When a = 4, b = ______________.
When a = 5, b = ______________.
Rewrite the equation so that Robert’s values are correct.
Answer:
Robert’s mistake is that he formed the operations wrong instead of doing multiplication first he did addition first.
The equation correctly to find the output values.
When a = 3, b = 24.
When a = 4, b = 25.
When a = 5, b = 26.
Explanation:
Equation: a + 7 × 3 = b.
When a = 3,
b = a + 7 × 3
b = 3 + 7 × 3
b = 3 + 21
b = 24.
When a = 4,
b = a + 7 × 3
b = 4 + 7 × 3
b = 4 + 21
b = 25.
When a = 5,
b = a + 7 × 3
b = 5 + 7 × 3
b = 5 + 21
b = 26.
Write About It
Question 13.
How do parentheses affect the value of expressions?
Answer:
Parentheses are used in math to show a part of a math expression or equation that must be solved first, before any other calculations are done.
Explanation:
In mathematics, parentheses are symbols used for grouping expressions, multiplying expressions, separating expressions, and several other uses. The symbols are written in more than one form. There are round, square, and squiggly brackets.
McGraw Hill My Math Grade 4 Chapter 7 Lesson 8 My Homework Answer Key
Practice
Use each equation to find each unknown.
Question 1.
(z + 3) × 2 = y
When z = 2, y = ____________.
Answer:
(z + 3) × 2 = y
When z = 2, y = 10.
Explanation:
(z + 3) × 2 = y
When z = 2,
y = (z + 3) × 2
y = (2 + 3) × 2
y = 5 × 2
y = 10.
Question 2.
4 + (g × 3) = m
When g = 3, m = _____________.
Answer:
4 + (g × 3) = m
When g = 3, m = 13.
Explanation:
4 + (g × 3) = m
When g = 3,
m = 4 + (g × 3)
m = 4 + (3 × 3)
m = 4 + 9
m = 13.
Question 3.
2 + (n × 7) = p
When n = 1, p = _____________.
Answer:
2 + (n × 7) = p
When n = 1, p = 9.
Explanation:
2 + (n × 7) = p
When n = 1,
p = 2 + (n × 7)
p = 2 + (1 × 7)
p = 2 + 7
p = 9.
Question 4.
(r × 2) + 6 = v
When r = 4, v = _____________.
Answer:
(r × 2) + 6 = v
When r = 4, v = 14.
Explanation:
(r × 2) + 6 = v
When r = 4,
v = (r × 2) + 6
v = (4 × 2) + 6
v = 8 + 6
v = 14.
Question 5.
6 + (a × 3) = b
When a = 5, b = _____________.
Answer:
6 + (a × 3) = b
When a = 5, b = 21.
Explanation:
6 + (a × 3) = b
When a = 5,
b = 6 + (a × 3)
b = 6 + (5 × 3)
b = 6 + 15
b = 21.
Question 6.
(j ÷ 4) + 8 = k
When j = 16, k = ______________.
Answer:
(j ÷ 4) + 8 = k
When j = 16, k = 12.
Explanation:
(j ÷ 4) + 8 = k
When j = 16,
k = (j ÷ 4) + 8
k = (16 ÷ 4) + 8
k = 4 + 8
k = 12.
Problem Solving
Question 7.
Set up an equation machine to show (x + 2) × 5 = y. Find the values of y when x = 5, x = 8, and x = 12.
When x = 5, y = _____________.
When x = 8, y = _____________.
When x = 12, y = ____________.
Answer:
Equation: (x + 2) × 5 = y.
When x = 5, y = 35.
When x = 8, y = 50.
When x = 12, y = 70.
Explanation:
Equation: (x + 2) × 5 = y.
When x = 5,
y = (x + 2) × 5
y = (5 + 2) × 5
y = 7 × 5
y = 35.
When x = 8,
y = (x + 2) × 5
y = (8 + 2) × 5
y = 10 × 5
y = 50.
When x = 12,
y = (x + 2) × 5
y = (12 + 2) × 5
y = 14 × 5
y = 70.
Question 8.
Mathematical PRACTICE Understand Symbols Bryan made up a game. Each team starts with seven points. Each time a team answers a question correctly, they earn five points. The equation used to find the total number of points is 7 + (5 × q) = t. Find the total number of points (f) when a team answers six questions (q) correctly.
Answer:
Total number of points (f) when a team answers six questions (q) correctly = 37.
Explanation:
Number of points each team starts = 7.
Number of points each teams gets when they answers a question correctly = 5.
Number of question they answered correctly(q) = 6.
Total number of points (f) when a team answers six questions (q) correctly =
t = 7 + (5 × q)
t = 7 + (5 × 6)
t = 7 + 30
t = 37.